横向气膜作用下液体射流在近喷孔区域的破碎雾化特性*

金烜 沈赤兵

1) (国防科技大学空天科学学院,高超声速冲压发动机技术重点实验室,长沙 410073)

2) (中国空气动力研究与发展中心,绵阳 621000)

1 引言

变推力液体火箭发动机在空间运输、交会对接、星际着陆等方面具有显著的优越性[1],而针栓式喷注器作为变推力发动机应用的典型,相对于传统的同轴离心式或直流撞击式喷注器具有结构简单、工况和推进剂组合适应性良好、燃烧高效稳定等优点[2].上述优点使针栓式喷注器获得了一系列成功应用,包括先后将12 名宇航员送上月球的阿波罗登月舱下降发动机LMDE(推力变比10∶1)[3]、实现月球表面软着陆的嫦娥三号探测器主发动机(推力变比5∶1)[4,5]、多次成功降落回收的猎鹰9 号火箭梅林1D 发动机(推力变比2∶1)[6].针栓式喷注器的喷雾特性关系着燃烧效率以及发动机工作可靠性[7].在液体火箭发动机的研制过程中,喷注器通常是所需周期最长的一个部件,其方案选择和结构设计也往往是应首先解决的关键技术.

针栓式喷注器已有半个多世纪的研发历史,但公开文献中关于喷雾机理的介绍却非常有限[8-11],尤其是径向孔型气液针栓式喷注器.目前该类型喷注器的射流破碎雾化过程的研究以数值模拟为主,试验观测仅作为辅助验证.Radhakrishnan 等[12,13]借助商用软件Fluent 提供的欧拉-拉格朗日体系描述径向液体射流在轴向气体来流作用下的二维破碎雾化过程,一次破碎和二次破碎过程分别用简单的Single 喷注模型和Wave 破碎模型(Kelvin-Helmholtz 不稳定主导)代替;Son 等[14]则利用Fluent开展欧拉多相流模型的二维轴对称仿真,该方法对液滴的捕捉能力受限于网格密度.Radhakrishnan和Son 的仿真结果仅能在针栓喷嘴的喷雾形态和喷雾锥角方面与试验结果吻合,无法模拟真实的气液作用界面和表面波发展过程.张彬[15,16]将Fluent的新功能VOF-to-DPM 模型结合三维网格自适应技术,成功捕捉到了在气膜作用下单股液体射流的两种破碎过程:液体射流迎风面和背风面之间的压差促使射流往下游弯曲,同时低密度气体对高密度液体产生的加速作用(Rayleigh-Taylor(R-T)不稳定性)导致射流迎风面出现表面波,其振幅随时间发展最终在波谷处发生断裂(柱状破碎);气流与液体射流的切向速度梯度则导致射流表面出现尺度远小于表面波的层状褶皱(Kelvin-Helmholtz(K-H)不稳定),随着褶皱拉伸变薄陆续有小液滴被气流剥离(表面破碎).随着局部动量比增大,柱状破碎逐渐取代表面破碎开始主导射流的一次破碎过程,表面波长逐渐增大至最大值,同时连续射流的断裂位置逐渐远离喷孔.林森[17]采用两相流大涡模拟程序[18,19]对单股矩形喷孔射流进行仿真得到了相似的破碎过程,同时研究发现当喷孔长宽比变大时,气动力作用随着气液接触面同步增大,射流破碎尺度减小,三维空间内液滴分布更为均匀.

径向孔型气液针栓式喷注器的射流破碎雾化过程与超/亚声速气流中的液体横向射流较为相似,差异主要在于液体射流穿透深度与气流来流厚度的相对大小,而研究人员针对后者已开展了大量工作,包括一次破碎模式和二次破碎模式的划分[20-22]和射流与液滴表面波产生机理与发展规律[19,23-25],结果表明液体射流的破碎雾化主要涉及R-T 不稳定和K-H 不稳定这两类机制,为前者的研究提供了参照.试验观测手段包括背景光成像法[8,24]、激光阴影法[26]和全息成像法[22],其中背景光成像的应用最为普及;捕捉气液界面的数值仿真方法包括体积分数法VOF (volume of fluid)[14]、水平集法LS (level set)[27]、CLSVOF(coupled LS and VOF)法[17-19,28]和VOF-to-DPM 法[16,29],其中CLSVOF和VOF-to-DPM 的效果更好.

针栓式发动机工作时喷雾往往集中于近喷孔区域内,液体射流从圆孔喷出后受气膜作用发生弯曲变形,伴随着气液界面不稳定波的产生和发展,连续射流逐渐破碎成液丝和液滴并迅速蒸发.因此近喷孔区域存在表面波主导破碎过程(一次破碎)和快速雾化过程(二次破碎),属于流体力学和两相流领域的研究难点,也是真正实现气液针栓式火箭发动机喷雾与燃烧“耦合计算”的主要问题.由于该区域复杂的两相流动耦合将产生大量空间尺度快速变化的特征结构,需要新的思路来克服径向孔型针栓式喷注器不同液体射流之间的相互干扰及其导致的背景光成像法有效性变差等问题.本文设计了一种采用空气和水为介质的针栓喷注单元作为研究对象,采用两相流大涡模拟和背景光成像相结合的方法对近喷孔区域的喷雾场的建立过程及其动态特性进行仿真与试验研究.

2 试验与仿真方案

2.1 气液针栓喷注单元工况设置

如图1 左侧所示的径向孔型气液针栓式发动机工作时,液体推进剂(Fluid-1)通过针栓中心流道后自针栓头端的一系列孔呈放射状径向喷出,气体推进剂(Fluid-2)从喷注器集气腔流经针栓外侧的环缝轴向喷出形成气膜,径向射流与轴向气膜呈90°交叉撞击后推进剂发生破碎雾化与混合燃烧.为了更好地观测径向液体射流与轴向气膜之间的碰撞过程,设计用于冷试的针栓喷注单元,采用过滤水和干燥空气来作为模拟介质.轴向喷注连续气膜,喷注面为长方形,径向孔喷注单股液体射流,将三维喷雾降维处理,增强可视化,以方便分析.

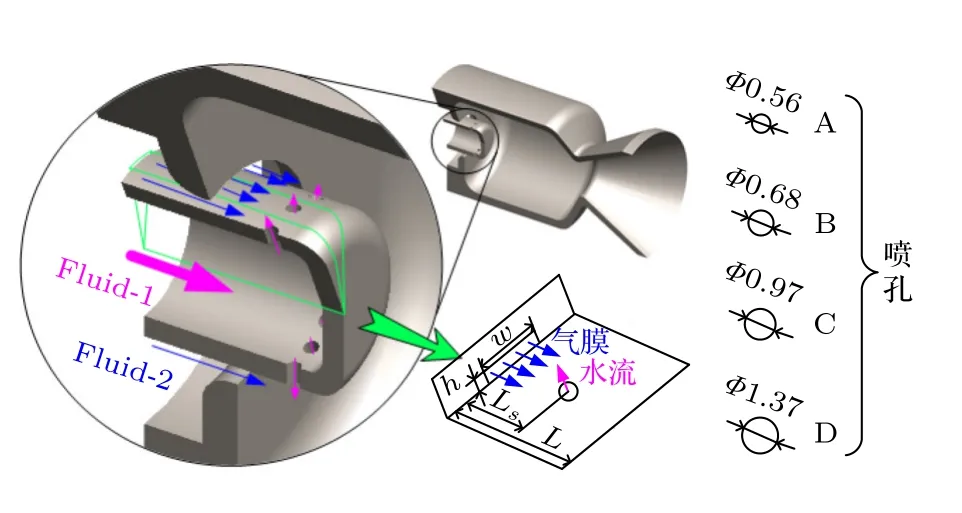
图1 针栓喷注单元结构示意图(单位:mm)Fig.1.Conceptual illustration of the gas-liquid pintle injector element (Unit:mm).

4 种不同尺寸的圆形喷孔见图1 右侧,其余主要结构参数如下:狭缝宽度w取7 mm,狭缝高度h取2.23 mm,跳过距离Ls取12 mm,针栓长度L取22 mm.针栓喷注单元装配体的具体结构如图2 所示,其中水流通道的轴向密封采用O 形圈实现,集气腔(盖板和底座之间)的密封采用紫铜垫片实现.

图2 针栓喷注单元装配图Fig.2.Final geometry of the pintle injection element assembly.

喷雾试验在静止空气环境中开展,环境温度取300 K,环境压力取101.3 kPa.在节流条件下空气和水的质量流量分别按如下公式计算:

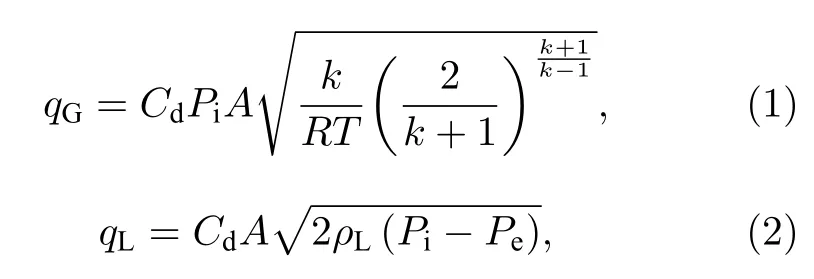
式中q表示质量流量,下标G 和L 分别表示气体和液体(在本文即为空气和水);Cd表示流量系数;A表示喷注通道的节流面积;Pe表示喷出压力,这里取环境压力;Pi表示喷前压力;T表示流体温度;R表示气体常数;k表示比热比.

冷试工况安排见表1,针对图1 右侧所示的4 种不同直径的射流喷孔,各自设定的水流质量流量与喷孔面积成正比(见表1 第2 列),并与6 种不同的空气喷注压降(即Pi与Pe之差,从大到小依次为2.13,0.99,0.62,0.42,0.31,0.24 MPa,与表1第2 行中从左至右的6 种不同空气质量流量相对应)进行组合共形成24 个冷试工况;v表示喷注速度,根据(1)式和(2)式计算可知vG在不同工况下略有变化,而vL保持33.48 m/s 不变.

表1 冷试工况设置Table 1.Operating conditions of cold tests.

2.2 喷雾试验与测量系统

冷态喷雾试验在常温常压下开展,雾化试验系统如图3 所示,包括模拟介质供应装置、喷雾收集器、试验件和压力流量测控装置等基本组成部分.试验过程中空气直接从高压气瓶中喷出,贮箱内的水则经高压氮气增压后喷出.空气和水进入针栓喷注单元时的入口压力和流量由减压阀和气动阀控制.喷雾收集器负责将液雾及时抽吸排出以免环境中液雾弥漫影响观测结果.

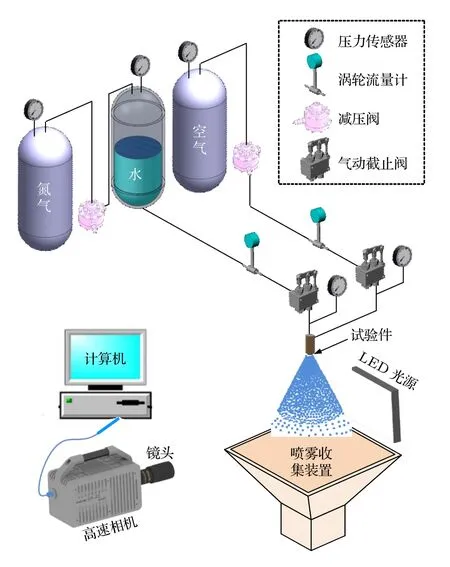
图3 试验系统示意图Fig.3.Schematic diagram of the experimental platform.

喷雾试验中需测量的常规参数包括各工质在试验系统中的贮箱压力、管路压力和喷前压力,以及各路工质在管路中的温度和流量.空气和水的体积流量测量均采用涡轮流量计,压力测量采用压阻式压力传感器,温度测量采用热电阻.需要注意的是空气质量流量的计算首先要基于流量计附近的温度和压力,根据理想气体方程得到空气的密度.另外喷雾场本身不发光且不易于被照亮,因此非常适合背景光成像进行拍摄.考虑到衡量气液撞击过程中连续液体射流破碎时间的特征时间尺度t*定义见(3)式,表1 所列工况的特征时间尺度t*对应的频率f均为10 kHz 量级.为了通过高速摄影结果准确识别该特征频率f,要求采用频率fs＞ 2f,因此本文中黑白高速相机的拍摄帧频和曝光时间分别取200 kHz 和1.25 µs.

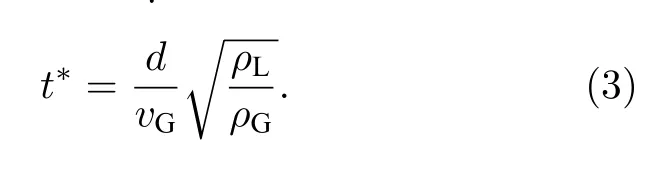
2.3 两相流大涡模拟

在超/亚声速气流中射流一次破碎和液滴二次破碎的研究中,肖锋等[18,19,25]提出了一种两相流大涡模拟算法,采用不可压流求解器和可压流求解器来分别计算液体和气体:采用有限体积法求解不可压流控制方程,时间离散和空间离散分别通过一阶正向投影方法和二阶中心差分方法实现;采用有限差分方法求解可压流控制方程,其中时间离散通过二阶TVD(total variation diminishing)和Runge-Kutta 方法实现,时间步长由取值0.4 的CFL (courant-friedrichs-lewy)数决定,空间离散采用五阶加权WENO(weighted essentially non-oscillatory)方法和二阶中心差分方法分别离散对流项和黏性项.构建笛卡尔网格进行求解时,不可压求解器中物理量交错分布(速度分量位于网格面,其他变量位于网格中心),而可压求解器中物理量均位于网格拐角;气相为不可压流求解器提供压力边界条件,液相为可压流求解器提供速度边界条件.另外该算法采用CLSVOF 法追踪气/液相界面,综合了LS 和VOF 的优点,既保证了相界面的连续性,又保证了质量守恒,已通过经典的液体射流一次破碎试验结果[22,30]验证了算法的准确性.

针栓喷注单元的水射流在空气膜撞击下的一次破碎过程与超/亚声速气流中的横向射流相类似,本文将采用肖锋等[18,19,25]提出的两相流大涡模拟算法对近喷孔区域圆孔液体射流的表面波主导破碎过程进行仿真研究.本文以图1 和图2 为参照构建了如图4 所示的长方体计算域,其左侧平面为包含射流喷孔出口面的基底面(设为壁面边界条件),上侧平面的左端为高2.23 mm 的气膜狭缝出口面(设为空气入口面,对狭缝长度不作限制以利于计算域分区),上侧平面的其余部分为腔盖面(设为壁面边界条件),计算域的其余外平面均设为出口边界条件.红色的液体射流从圆孔喷出后在气膜作用破碎雾化,当液滴尺寸小于所在位置的网格即消失不见,计算过程中以水射流的初始方向为x轴,空气射流的初始方向为y轴,展向为z轴.整个计算域尺寸(x×y×z)为50 mm × 100 mm ×40 mm,被划分为网格数量相等的256 个块后可在256 个核上实现并行计算;为降低计算成本,针对射流发生一次破碎的近喷孔区域进行加密处理(即通过划分小尺寸块以提高网格密度).

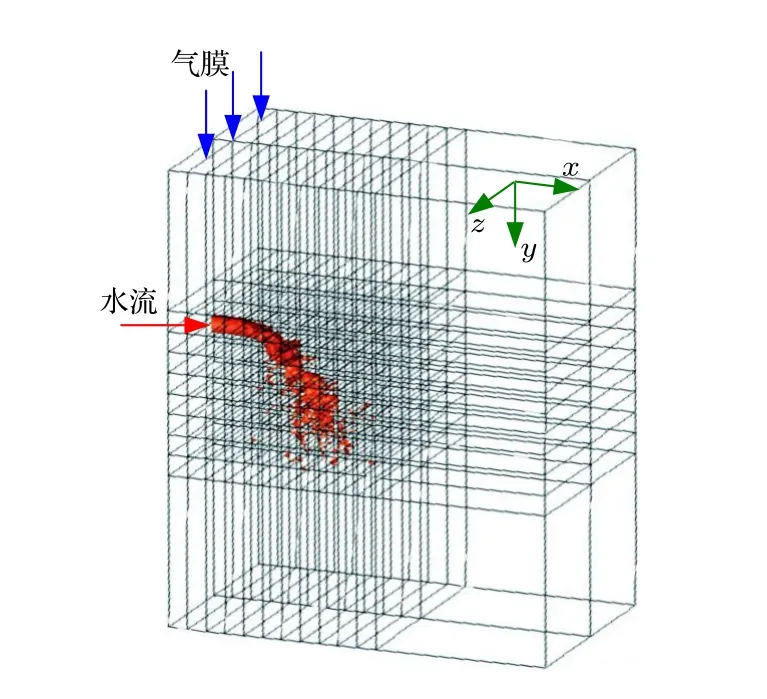
图4 计算域划分示意图Fig.4.Schematic diagram of the computational domain division.

3 结果分析与讨论

3.1 表面波主导破碎过程

近喷孔区域液体横向射流的破碎雾化是气动力、液体黏性力和表面张力的相互作用结果,其中气动力促使液体表面扰动的生成与发展,液体黏性力对液体表面扰动的发展有阻尼作用,而表面张力则有利于维持液体的聚集状态.因此破碎雾化类型通常基于韦伯数(见(4)式)和Ohnesorge 数(见(5)式)进行划分[22],前者表示气动力与表面张力之比,后者表示液体黏性力与表面张力之比.本节针对表1 中的工况CT14#研究圆孔射流在气膜作用下的表面波主导破碎过程,并分析破碎雾化典型特征和流场涡结构,该工况的韦伯数为4350,Ohnesorge数为0.00324,因此一次破碎过程形态上均属于剪切破碎.

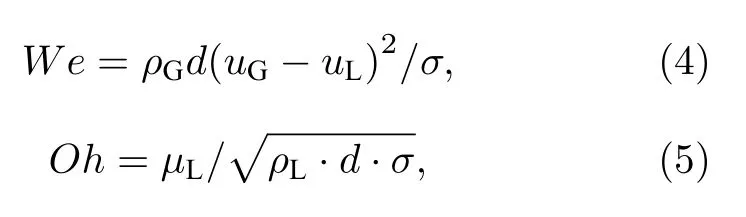
式中,d表示圆孔直径,σ为表面张力,µL为液体黏度.

仿真过程中在喷孔C(d=0.97 mm)出口面指定具有33.48 m/s 法向初始速度的水射流(qL=24.54 g/s),在狭缝出口面指定具有265.22 m/s 法向初始速度的空气射流(qG=33.41 g/s).参照文献[17,19]以加密区网格尺度为25 µm(约0.026d)的计算网格为基准(总网格量在4800 万左右),同时额外设置两套对比网格A 和B,加密区网格尺度分别为35 µm 和50 µm.

文献[24]提出“喷雾分数”概念以表示任一空间点(以像素点等价代替)被液体射流/喷雾占据的概率值,定义为

其中gi代表第i个样本图像中待计算空间点处的灰度值,n代表样本图像总数(取值越大越接近真实结果).通过对工况CT14#的1500 幅连续喷雾图像进行统计,提取出如图5(a)所示的近喷孔区域的时均射流/液雾边界带,边界带右上方和左下方分别表示恒气相区(γ=0)和恒液雾区(γ=1),喷雾分数介于0 到1 之间的边界带对应射流/喷雾边界的振荡,其中包含若干条喷雾分数等值线,任意一条喷雾分数等值线均可被视为是液体射流/喷雾的时均边界.本文将网格加密区内若干时刻的射流/液雾分布结果(通过红色的气液界面表示)叠加得到其射流/液雾穿透深度,对比图5(b)—(d)可以发现计算网格和对比网格A 的结果与喷雾分数γ=0.1 等值线表示的喷雾场外边界基本吻合(误差将在下文进一步解释),而对比网格B 的结果与试验结果的差异较为显著,验证了计算网格、对比网格A 和该计算方法对气液针栓式喷注器一次破碎过程仿真的适用性.这里采用γ=0.1 等值线而非γ=0 等值线,是因为后者受小尺度液滴影响在边界带中不太稳定,不适合代表真正的喷雾分布范围.如无特别说明,本节均采用计算网格以提高对液滴的捕捉能力.

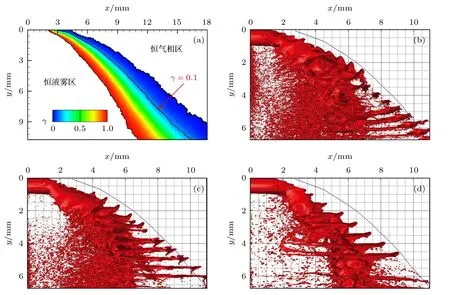
图5 关于工况CT14#中射流/液雾分布范围的仿真结果(红色气液界面)与试验数据(蓝色的喷雾分数γ=0.1 等值线)对比(a) 时均射流/液雾边界带;(b) 计算网格;(c) 对比网格A;(d) 对比网格BFig.5.Comparison of LES-predicted liquid jet/spray distribution (gas-liquid interface colored by red) for case CT14# with experimental data (i.e.the blue spray fraction iso-line of γ=0.1):(a) time-averaged boundary band;(b) computing grid;(c) contrast grid A;(d) contrast grid B.

从图6 给出的瞬时压力和速度云图可以看出,射流上方的空气压力和流速相比于气膜狭缝出口分别出现了显著的下降和上升,说明气膜到达喷孔位置前经历了膨胀加速过程,其在x方向的作用范围也大大超过了狭缝高度(2.23 mm).由于横向喷出的水射流对高速空气来流产生阻挡作用,射流前方出现一道较强的脱体弓形激波①.在弓形激波最靠近壁面处,其与空气来流的夹角接近90°,这是由于水射流离开喷孔后的初始阶段基本未发生变形,其对高速空气来流的阻挡作用与横向放置的圆柱相似.高速空气来临通过弓形激波后压力与速度分别剧烈升高和下降,进而在到达气液交界面时发生滞止并绕过水射流迎风面往下游流动,气液动量交换将促使射流发生弯曲变形;同时绕流运动产生的流动分离现象导致射流背风面出现低压区,故射流前后压差也将产生一个垂直射流表面并促进弯曲变形的加速度.

图6 工况CT14#中瞬时液体射流形态对应的 (a)压力云图与(b)速度云图Fig.6.(a) Instantaneous pressure and (b) velocity contours of case CT14#,together with the liquid jet structure.

需要注意的是弓形激波并非从壁面生成,弓形激波后侧的高压区产生逆压梯度并经由边界层的亚声速区往上游传递,导致水射流上游的边界层发生转捩和变厚,形成图6(b)中较为明显的分离区②,因此弓形激波是在其上方产生(激波结构只存在于超声速气流中).

随着水射流远离喷孔,其逐渐往空气来流方向弯曲且气液速度差有所减小,而弓形激波由初始的正激波转变为斜激波且强度逐渐减弱,当弓形激波到达右侧的高速空气来流作用边界时消失.从图6(a)中还可以发现,在离开喷孔一定距离后,存在个别小激波③从水射流迎风面突起处往外延伸至弓形激波上,小激波生成的位置及强度有一定随机性,分析认为高速空气来流经弓形激波减速后相比水射流依然保持较大速度差,射流表面的流动受到突起结构的阻碍是形成小激波的原因.

如图6 所示,连续射流发生弯曲变形过程中始终存在一个与其流向相垂直的气动力,即低密度气体对高密度液体产生法向加速度,因此水射流将受到R-T 不稳定性的影响,表现为迎风面表面波沿水射流流向的发展[22].图7 给出了试验和不同网格仿真得到的典型R-T 不稳定表面波沿射流迎风面的发展规律,其中试验结果通过显化处理得到,即在灰度值线性拉伸的基础上再通过幂变换进行非线性拉伸,从而凸显表面波和连续射流断裂位置等特征结构,本文采用的幂变换函数为

图7 工况CT14#中典型R-T 不稳定表面波形态的试验[(a)—(b)]与仿真[(c)—(h)]对比:(a) t1 (试验结果);(b) t1+15 µs (试验结果);(c) t2 (计算网格仿真结果);(d) t2+15 µs(计算网格仿真结果);(e) t3 (对比网格A 仿真结果);(f) t3+15 µs (对比网格A 仿真结果);(g) t4 (对比网格B 仿真结果);(h) t4+15 µs (对比网格B 仿真结果)Fig.7.Comparison of experimental [(a)—(b)] and simulation [(c)—(h)] results of case CT14# on the distribution of typical R-T unsteady surface waves:(a) t1 (experimental result);(b) t1+15 µs (experimental result);(c) t2 (simulation result of computing grid);(d) t2+15 µs (simulation result of computing grid);(e) t3 (simulation result of contrast grid A);(f) t3+15 µs (simulation result of contrast grid A);(g) t4 (simulation result of contrast grid B);(h) t4+15 µs(simulation result of contrast grid B).

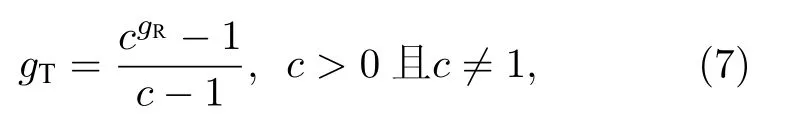
其中gR和gT分别代表幂变换前后图中的相对灰度值,c为非线性系数(c＜ 1 时可显化小灰度值区域,c＞ 1 时可显化大灰度值区域,此处c取10).

从图7 可以看出,随着表面波波长与振幅的不断增长,水射流在展向和流向同时受到拉伸而不断变薄,结合图6(b)所示的速度云图和图8 所示的涡结构可以认为连续射流发生断裂前波谷处易形成低速漩涡结构(柱状破碎涡,column breakup vortices),加剧气液两相之间的相互作用;当表面张力无法抵抗气动力时连续射流将波谷处发生断裂,同时在压差作用下高速气流自断裂位置进入,将大量剥离出的液滴往壁面附近输运从而形成拉丝现象,围绕液滴和液丝生成的涡将对二次破碎和混合特性产生重要影响.另外喷孔附近还捕捉到由未发生变形液束与壁面边界层之间的相互作用激发形成的马蹄涡(horseshoe vortices).总的来说,气液针栓式喷注器的表面波主导破碎过程与超声速气流中液体横向射流的破碎过程有一定相似性[24].

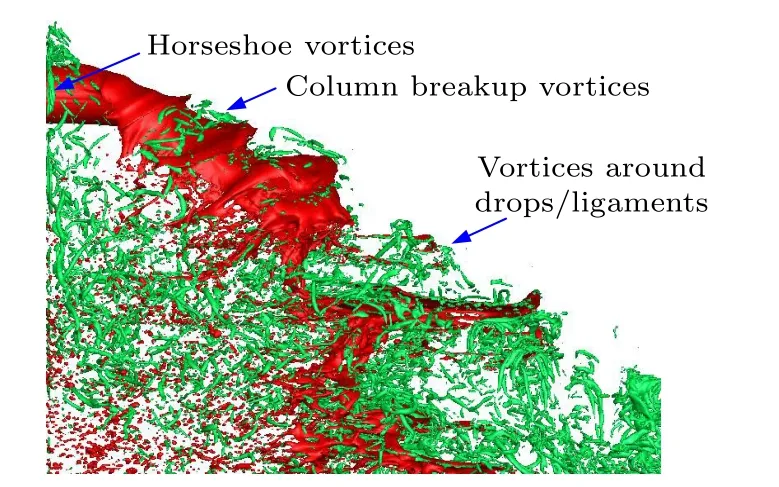
图8 工况CT14#中瞬时射流结构(红色)与涡结构(绿色)的叠加图,其中涡结构由速度梯度第二不变量[31]的等值面表示Fig.8.Instantaneous liquid jet structure (colored by red) of case CT14#,superimposed with the vertical structures identified by isosurface of the second invariance of the velocity gradient tensor (colored by green).

图7 中通过对比表面波波长还可发现:计算网格和对比网格A 仿真得到的表面波形态与试验结果基本相同,同时时间间隔较短的情况下前后两幅图像具有明显的时间相关性(即具有相同的特征结构),有利于对表面波主导破碎过程中特征结构的时间演化特性和速度变化规律开展研究;而对比网格B 仿真得到的表面波形态与试验结果差异较大且时间相关性较差,因此该网格无法满足计算精度.图7 中计算网格和对比网格A 的仿真结果相对于试验结果的不足主要在于仿真无法得到沿连续射流分布的浓密液雾,原因为仿真计算难以捕捉小于网格尺寸的液滴颗粒,特别是气液切向速度梯度诱发K-H 不稳定而剥离的大量小尺寸液滴;喷孔附近较为浓密的液雾是由于亚声速流动的分离区内存在旋转方向相反的分离涡与再附涡,能将小尺寸液滴沿分离区往上游传递,但在仿真结果中同样不是很明显.

3.2 破碎雾化过程的动态特性分析

如前所述,表面波主导破碎过程对气液针栓喷注单元的喷雾特性有重要影响,本节选取典型的工况CT17#进一步分析近喷孔区域的破碎雾化过程的动态特性.对工况CT17#的连续喷雾图像采用POD 方法(原理介绍参见文献[7])分析其拟序结构,图9(a)和图9(b)所示为其连续喷雾的某时刻瞬态图像和时均结果,图9(c)—(h)为表征喷雾流场的特征结构的若干POD 模态(对应时间系数的功率谱见图10),其中模态云图幅值越大(即颜色越深)说明该处的动态特征越强,同时比其余幅值较低处对于整体振荡的贡献越大.

图9 工况CT17#的(a)瞬时喷雾图像,(b)时均结果及(c)—(h)若干POD 模态Fig.9.(a) Spray snapshot,(b) time average and (c)—(h) several POD modes of case CT17#.

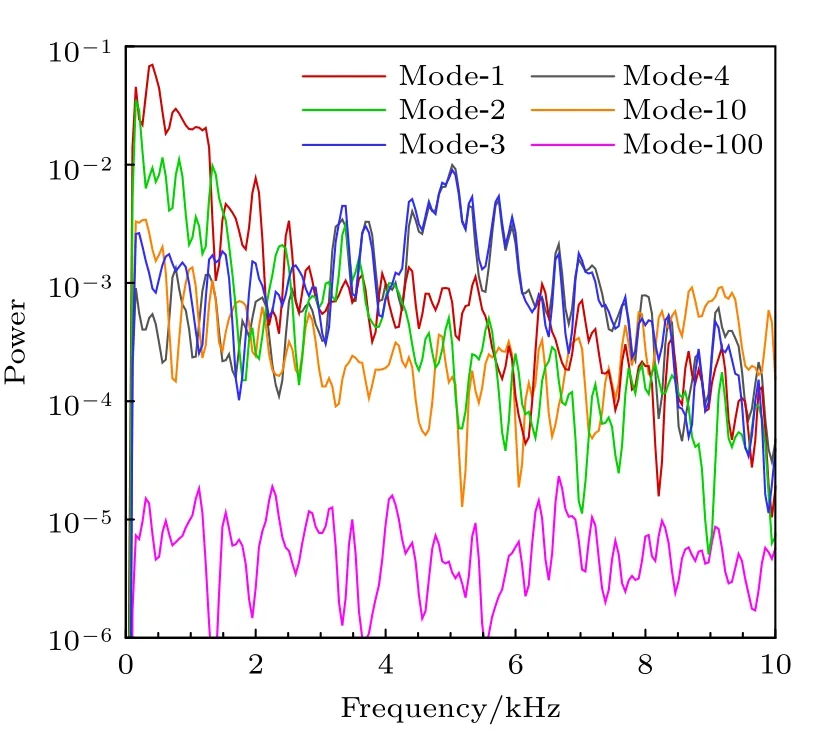
图10 工况CT17#若干POD 模态的时间系数功率谱叠加图Fig.10.Superposition of the power spectrum densities from several POD modes of case CT17#.

从图9 中的POD 模态可以看出工况CT17#的喷雾振荡主要包含两类特征:模态1 和模态2 中沿喷雾外边界法向出现幅值及其符号的剧烈变化,表明喷雾流场存在整体扩张/收缩过程,虽然相应功率谱的幅值较大,但主频在1 kHz 以下,主要受上游管路振荡引起的气液介质流量变化影响;模态3 和模态4 沿喷雾迎风面呈现出比较规则的空间周期性结构,主要源于连续射流断裂后形成的液块或液雾团在气流作用下往下游运动,这两个模态的功率谱基本一致,无明显主频,但在3—6 kHz范围内有较大能量.后续的模态10,基本可认为是前4 个模态的组合或高阶谐振(包括中低频和高频等多个主频),未提供值得关注的新特征;而模态100 在空间结构和功率谱均趋于均匀化,类似于高速摄影采样频率下的噪声.另外前4 个模态喷雾振荡的能量贡献(energy contribution,EC)较大并快速下降,后续模态的能量贡献则处于缓慢减小的趋势.

模态3 和模态4 的空间结构与撞击式喷嘴研究中的“撞击波”概念[32]类似,即当韦伯数超过临界值后,将从撞击点辐射出撞击波.从图10 已知模态3 和模态4 的时间系数功率谱基本一致,通过交叉功率谱CPSD(cross-power spectrum density,相关介绍参见文献[33])进一步分析两者时间系数的相关联,图11 的结果显示,在交叉功率谱的能量较大的频段(3—6 kHz)两者的相位差为90°左右,且图9(e)和图9(f)显示这两个模态空间结构相差四分之一波长,故可认为两者相互耦合形成了正弦或余弦状的行波结构.通常认为单个行波由两个驻波叠加而成,模态3 和模态4(以Φ3和Φ4表示,相应时间系数为a3和a4)叠加后形成的行波可近似为

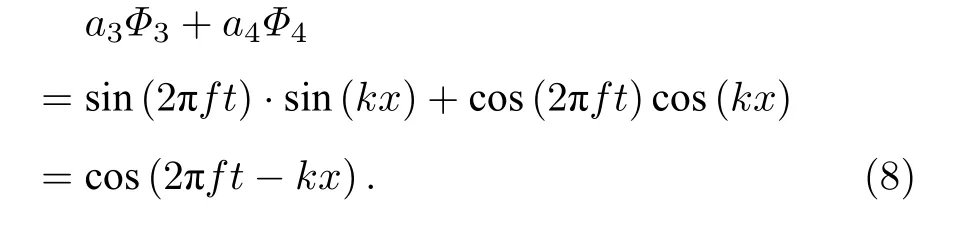
图11 工况CT17#的POD 模态3 和4 时间系数的交叉功率谱幅值和相位角Fig.11.Amplitude and phase angle from CPSD (Mode-3 and Mode-4) of case CT17#.

图12 展示了工况CT05#,CT11#和CT23#中耦合产生行波结构的POD 模态,其中工况CT23#中相关模态的位置有所变化,可认为该行波结构在横向射流中广泛存在.从POD 模态中提取喷雾迎风面行波结构的波长可避免从单个喷雾图像计算波长产生的误差.如图13 所示,表1 中不同工况下无量纲行波波长(λ/d,波长与孔径的比值)和韦伯数之间呈幂次律关系,经拟合得到吻合度良好(R2=96.98%)的如下关系式:

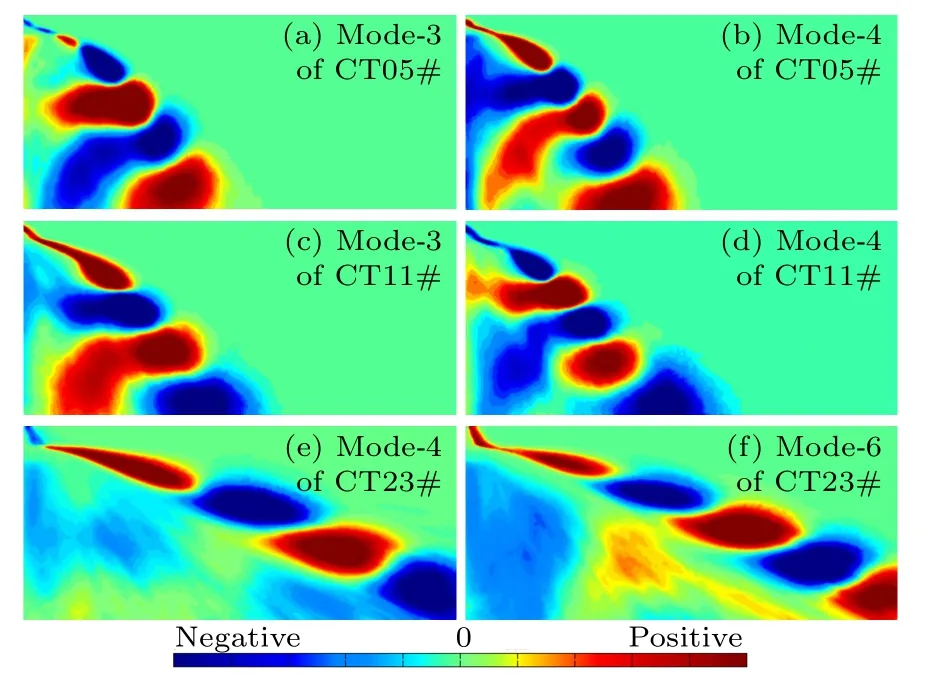
图12 工况CT05#,CT11#和CT23#中耦合产生行波结构的POD 模态Fig.12.POD modes that generate the traveling wave structure in case CT05#,CT11# and CT23#.

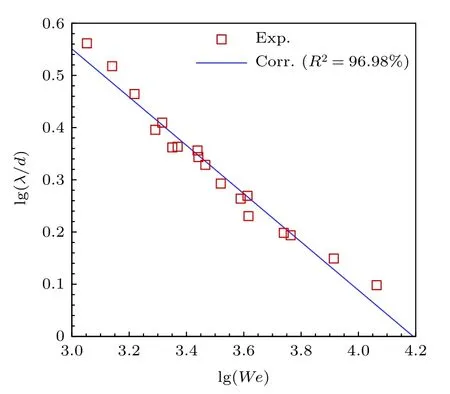
图13 无量纲行波波长与韦伯数变化的关系Fig.13.Variation of dimensionless surface wavelength versus Weber number.

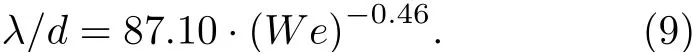
在R-T 不稳定表面波主导的一次破碎过程中,对应最大增长率的表面波波长λR-T的计算公式为

式中,σ和ρL分别为液体表面张力和密度,a为液体射流的加速度,

其中CD为有效阻力系数,根据文献[19]对亚声速气流中液体横向射流一次破碎过程大涡模拟研究可知CD∝We-0.1.将加速度a的表达式代入(10)式,同时考虑到uG远大于uL,(4)式中uL的影响可忽略,无量纲表面波波长(λR-T/d)的表达式简化后与We的关系呈—0.45 幂次的规律:

因此可认为(9)式所代表的一次破碎后液块或液雾团在近场区域迎风面的波动是连续液体射流断裂前的R-T 不稳定表面波的延续.

最后通过瞬时喷雾图像重构来说明POD 方法的有效性.假设两张图像(xp和xq)的像素分辨率均为m×n,两者之间的乘积(xp·xq)定义如下:

由前M个模态重构K个时刻的喷雾图像,重构误差εM如下所示:

式中,Ut为t时刻的瞬时喷雾图像,Φi为第i个模态,ai,t为模态i的在t时刻的时间系数(需要注意的是Φ0为K个时刻喷雾图像的时均结果,a0,t始终为1).

针对图9(a)所示的瞬时喷雾图像,采用前M个模态进行图像重构,重构结果及其误差见图14.在图9(b)所示的时均结果基础上,前20 个模态的叠加结果主要重构出了最显著的结构特征,重构误差已降至0.5 以下;随着参与重构的模态数量增至200,连续射流表面波和一次破碎后液块或液雾团的波动结构逐渐显现,重构误差为0.15 左右,其下降速率逐渐减弱;而当M取1000 时已重构得到较为清晰的液滴分布,证明POD 方法应用于喷雾图像模态分析的有效性,此时重构误差仅0.03 左右,但其下降速率进一步减小,也说明单个模态的影响已微乎其微.图15 则展示了工况CT05#,CT11#,CT17#和CT23#中瞬时喷雾图像重构误差的统计结果,随着参与图像重构的模态数量的增加,每个工况中重构误差的减小趋势相同,同时相同空气流量下通过改变孔径增大液体流量将导致重构误差增大.

图14 工况CT17#的瞬时喷雾图像重构Fig.14.Image reconstruction of spray snapshot from case CT17#.

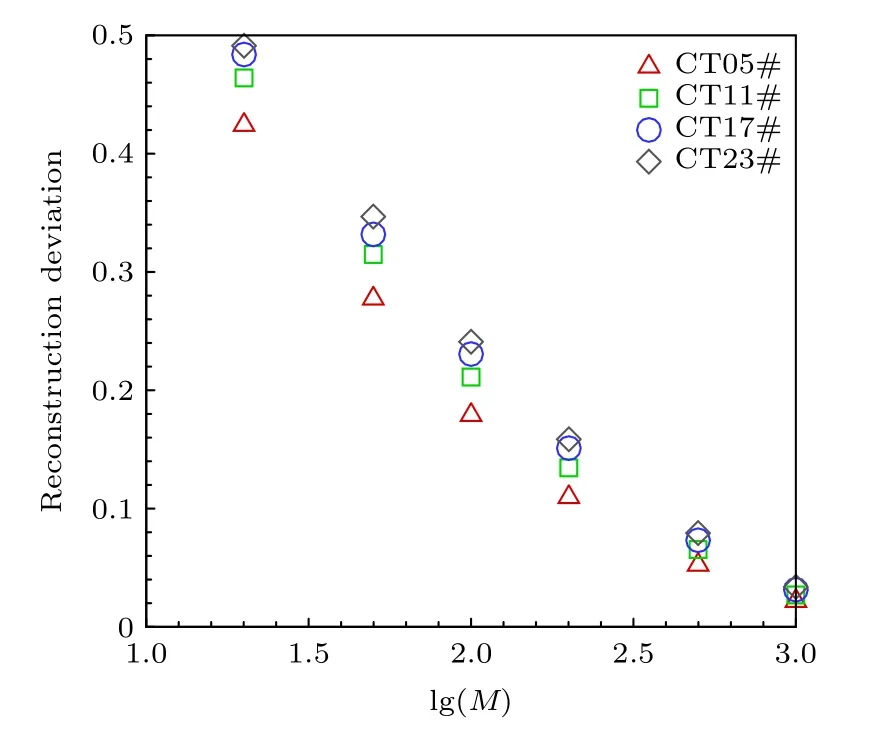
图15 部分工况中重构误差的统计结果Fig.15.Statistical results of the reconstruction deviation in several cases.

4 结论

本文以空气和水为模拟介质,通过两相流大涡模拟和喷雾背景光成像,分析了横向气膜作用下液体射流在近喷孔区域的破碎雾化过程及其动态特性,具体得到如下结论.

1)近喷孔区域的气液流场建立过程为:亚声速气流离开狭缝后膨胀加速为超声速气流,液体射流垂直进入气体来流,射流上游产生脱体弓形激波.液体射流在气体来流的作用下逐渐向下游弯曲,相应的弓形激波由初始的正激波转变为斜激波且强度逐渐减弱.而射流迎风面在压差作用下出现R-T不稳定表面波,表面波的发展导致连续射流在波谷处发生断裂,气流自断裂位置进入后将大量剥离出的液滴往壁面附近输运从而形成拉丝现象.

2) POD 方法可有效重构冷态试验中获得的瞬时喷雾图像,POD 模态表明近喷孔区域的喷雾振荡主要由喷雾场的整体扩张/收缩过程(低频)和液块或者液雾团在迎风面的运动构成,其中后者是具有高频振荡的行波结构.无量纲行波波长和R-T不稳定表面波波长与韦伯数之间的幂次律关系十分相近,可认为该行波结构受连续液体射流断裂前的R-T 不稳定影响而产生.