基于GARCH-VaR模型的股票市场风险管理
2022-06-18李欢刘春莉彭丹妮
李欢 刘春莉 彭丹妮


摘要:本文主要讨论基于GARCH-VaR模型的股票市场风险管理。通过对上证指数收盘价数据分析处理,运用GARCH(1,2)模型,采用正态分布方法计算VaR的值,得到不同置信水平下对应的VaR值,最后通過后验测试,确定模型精度。
关键词:VaR方法;风险管理;GARCH模型
1. 引言
随着中国股票市场的发展,投资者对股票市场投资风险越来越关注,股票市场的风险准确性测度对于投资者风险管理有着重要意义。同时,股票市场的风险度量问题也成为众多学者关注的热点。在众多的金融风险管理工具中,VaR方法以其快速、简单、便捷的特征被广泛应用。李翠霞等[1]对道琼斯指数进行研究,建立GARCH(1,1)模型,修正残差后得到更准确的VaR计算模型。姚萍等[2]运用两类EGARCH模型估算VaR的预测值。白娟娟等[3]对样本数据进行检验,建立模型并求得VaR的值,最后研究发现该模型提高了预测VaR的精度。王杰等[4]以美股三大收盘价数据为基础进行研究,计算其对数收益率,运用HGARCH族模型计算VaR的值,分析结果显示该模型能够准确预测,具有极强的实际应用性。宋敏等[5]采用GARCH(1,1)模型对碳金融市场进行研究,计算在特定持有期内不同置信度水平下的VaR。Li等[6]基于沪深300指数,利用蒙特卡罗模拟和历史模拟计算五年期指数的VaR并测试其有效性,并对中国金融市场的金融风险管理提出了一些对策和建议。Jiang[7]选取上市商业银行的日收盘价数据建立AR-GARCH模型,结果表明国有商业银行风险较低,自身风险处理能力较强;城市商业银行的自身风险较高,应对自身风险的能力较弱。Cui等[8]选取了上证综指和11个代表性板块指数,建立GARCH模型,最后从风险管理的角度为投资者提出了建议。
2 计量模型
2.1 风险价值VaR模型
风险价值是指在某个特定的持有期内,在确定的置信水平下,市场中的风险要素,比如利率、汇率等的变化对公司造成的潜在最大损失,可以表示为:
其中,表示概率测度,表示组合在未来持有期内的损失,表示组合在当前时刻的价值,为置信水平,VaR为置信水平下组合的风险价值。
假定投资回报率服从以为均值,为标准差的正态分布,在置信水平下,则资产组合在给定置信水平下的最小收益率为:
在标准正态分布下的VaR计算公式如下所示:
2.2 GARCH模型
GARCH模型如下所示:
其中是的样本均值,是残差,是方差,是常数,和是相应的参数。
3. GARCH-VaR模型在上证股票市场风险管理中的实证分析
3.1 GARCH模型的建立及参数估计
本文选取2018年1月2日至2021年12月31日上证指数收盘价数据进行分析。首先对数据进行对数化处理,运用公式,其中是第日的收盘价格,是第日前一天的收盘价格,为指数的对数收益率。通过对上证指数对数收益率序列分析,可以判定其是平稳的时间序列。
由上表可知对数收益率的峰度为7.994498大于3,具有明显的尖峰效应,偏度为-0.594415小于0,具有一定的负偏斜,该序列具有较长的左拖尾,有明显的尖峰厚尾特征,认为该序列不服从正态分布。
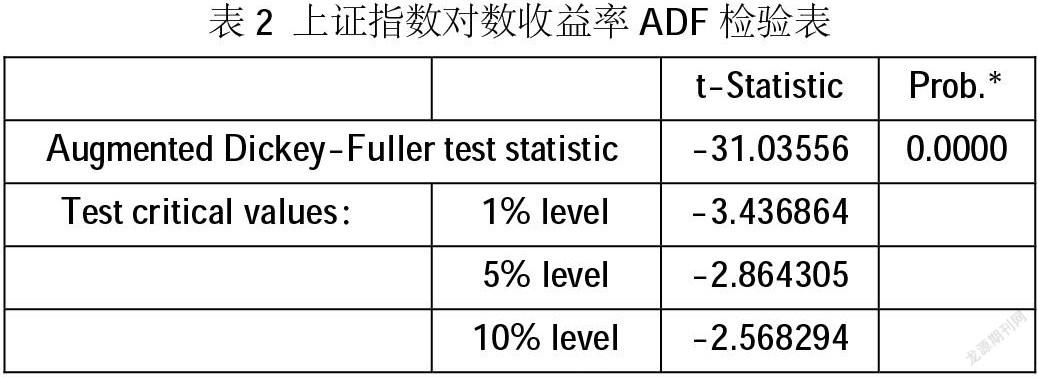
对序列进行ADF单位根检验,通过Eviews软件得到上证指数对数收益率时间序列的ADF统计值为-31.03556,相对照的1%、5%、10%的检验水平下的临界值分别为-3.436864、-2.864305、-2.568294,该序列的ADF统计值远小于不同的检验水平下的临界值,同时P值为0,P值小于0.05,所以在90%、95%、99%的显著水平下拒绝原假设,即对数收益率序列不存在单位根,该序列是平稳序列。
对序列进行自相关和偏自相关性检验,发现从整体来说,自相关系数与偏自相关系数均近似于0,大部分阶数对应的P值都明显大于0.05,因此不拒绝自相关函数值为零的假设,认为上证指数收益率之间相关性并不显著,不存在序列的自相关和偏自相关。
对序列进行ARCH效应检验,ARCH-LM检验结果如下表所示:
F统计量的P值为0.0379小于0.05,是显著的,表明收益率残差序列存在ARCH效应,可以说明对数收益率序列存在异方差特征,适合建立GARCH模型。
通过比较不同模型在正态分布下的参数来确定模型的优劣程度,本文选择GARCH(1,1)、GARCH(1,2)、GARCH(2,1)模型,模型的AIC 值和SC值如下表所示:
通过观察上表可以发现,AIC值和SC值最小的模型是GARCH(1,2)模型,因此选择这个模型来进行数据拟合。GARCH(1,2)模型表达式如下所示:
运用Eviews软件对GARCH(1,2)模型的预测值、残差和实际值进行绘图,如下图所示:
从上图可以看到预测值与实际值的波动趋势大致相同,认为所选择的GARCH(1,2)模型的精确度很高,模型选择的合理性得到验证。
3.2 VaR的计算
利用Eviews软件生成GARCH(1,2)模型中的方差序列,再通过计算得到标准差,由于研究需要,按照组合正态方法计算VaR的值。假设初始投资额为1,则下一期在不同置信水平下的VaR值如下表所示:
由上表可知:在置信水平为90%的情况下,相对应的VaR值为0.013911529,在置信水平为95%的情况下,相对应的VaR值为0.016575439,在置信水平为99%的情况下,相对应的VaR值为0.02181869。
3.3 VaR模型的后验测试
将选取的973个交易日内的上证指数对数收益率的VaR值和收益率进行大小比较,为避免符号的影响,将-VaR与对数收益率进行比较,前者大于后者则为对应的溢出天数,溢出天数与总天数相比则得到溢出率,再与不同的置信水平相比较,便可以得到VaR模型的精确度。测试结果如下表所示:F113ADAF-CFF6-4D10-A660-AD1C5065D574
根据测试结果表可以得出以下结论:
(1)在置信水平为90%的条件下,溢出率是4.419%,远远小于10%,因此在这种条件下溢出率很低,模型的精确度高;(2)在置信水平为95%的条件下,溢出率是3.186%,略微小于5%,因此在这种条件下溢出率较低,模型的精确度较高;(3)在置信水平为99%的条件下,溢出率是1.439%,稍微大于1%,因此在这种条件下溢出率较高,模型的精确度较低。综合各方面考虑,GARCH(1,2)模型的精确度较高,在90%和95%的置信水平条件下能够很好地应用于上证股票市场风险的度量。
参考文献:
[1]李翠霞,陈媛媛. 基于经验分布下GARCH模型对VaR的金融测度[J]. 中山大学学报(自然科学版),2021,60(4):177-182.
[2]姚萍,王杰,杨爱军,刘晓星. 基于EGB2分布族的GAS-EGARCH模型与VaR预测[J].运筹与管理,2019,28(11):125-134.
[3]白娟娟,師荣蓉. 基于广义已实现测度的中国股市波动预测与VaR度量[J]. 系统科学与数学,2021,41(3):653-666.
[4]王杰,杨爱军,林金官. 基于AST分布和HGARCH模型的金融资产收益率波动非对称性刻画与VaR预测[J]. 数理统计与管理,2020,39(6):1121-1140.
[5]宋敏,辛强,贺易楠. 碳金融交易市场风险的VaR度量与防控——基于中国五所碳排放权交易所的分析[J]. 西安财经大学学报,2020,33(3):120-128.
[6]Yunsi Li,Aihua Li,Zhidong Liu. Two ways of calculating VaR in risk management-an empirical study based on CSI 300 Index[J]. Procedia Computer Science,2018,139:432-439.
[7]Weidong Jiang. The application of VaR method in risk management of Chinese listed commercial banks[J]. World Scientific Research Journal,2020,6(6):234-249.
[8]Yiwen Cui,Lei Li,Zijie Tang. Risk analysis of China stock market during economic downturns-based on GARCH-VaR and wavelet transformation approaches[J]. Asian Economic and Financial Review,2021,11(4):322–336.
基金项目:国家级大学生创新训练项目(202110363107);安徽工程大学教研项目(2021jyxm23)。F113ADAF-CFF6-4D10-A660-AD1C5065D574
