基于改进JPS和A*算法的组合路径规划①
2022-06-17黄卫华李传奇何佳乐
金 震 黄卫华 李传奇 何佳乐
(*武汉科技大学机器人与智能系统研究院 武汉430081)
(**武汉科技大学冶金自动化与检测技术教育部工程研究中心 武汉430081)
(***武汉科技大学信息科学与工程学院 武汉430081)
0 引言
移动机器人的路径规划是指机器人遵循一些优化指标(比如时间最短、路程最优和能耗最低等),在具有障碍物的环境中寻找一条从起始状态到目标状态的无碰撞路径[1]。在图搜索类全局路径搜索算法中,A*算法是一种较为稳定的启发式路径算法,已广泛应用于路径规划领域。然而,A*算法在每步评价过程中,均会查询open 列表和close 列表中节点的状态,导致A*算法搜索效率较低,尤其是当环境存在对称路径时,A*算法耗费代价大,影响路径规划的实时性。2011 年,文献[2]提出了跳点搜索(jump point search,JPS)算法。在路径搜索中,JPS 算法删减大量的对称性中间节点和无用节点,保留了具有代表性的跳点,从而减少不必要的搜索路径,由此改善A*算法小步移动的缺点,有效提高了路径搜索效率[3]。
在应用过程中,JPS 算法简单且高效,但其适用于具有一定规律、大开放区域的地图进行路径规划,也就是通过在矩形区域内跳过大量对称路径,寻找关键跳点作为路径搜索的节点。为进一步提高JPS算法的性能,学者们提出了改进方法。文献[4]针对移动机器人在复杂环境下对智能性、高效性和可靠性的要求,提出了一种“块”操作方法以加快搜索跳点的速度,并删减了一部分仅代表路径方向发生改变的中间转折节点。文献[5]针对JPS 算法规划的路径可能存在碰撞的问题,将跳点进行危险度评估,改进了跳点的筛选方式,并且对障碍物进行膨化处理,从而降低了平均危险碰撞度。文献[6]改进了JPS 的搜索规则,以得到更多具有价值的路径并使用多段高阶多项式对所得路径进行轨迹优化。文献[7]针对JPS 算法存在路径搜索时间长等问题,提出了一种双向跳点搜索算法,从正、反两个方向采用改进的JPS 算法交替进行路径搜索。综合上述研究,JPS 算法主要是通过改进修剪规则和跳跃规则体现其优于A*算法的路径搜索效率。然而,相比于A*算法,JPS 算法在图裁剪的过程中往往需要评估更多的障碍物,尤其是当其所规划的路径过于靠近障碍物,常规对角线的跳跃方式极易发生碰撞,搜索到的路径存在一定的安全隐患;此外,当地图规模较大或对称性路径较少的时候,JPS 算法存在搜索到的跳点多且混乱的问题,一定程度上影响了路径搜索的效率。
考虑JPS 算法和A*算法的特点,本文提出了一种基于改进JPS 算法和A*算法的组合规划算法。首先,针对JPS 算法的跳点筛选规则进行改进并删除冗余的中间跳点,同时禁止机器人对角线穿越障碍物,并通过所设计的安全性评估模型保证搜索路径的安全性。然后,考虑到环境地图中具有对称性和非对称性路径规划的问题,设计了跳点阈值函数,构成基于改进JPS 和A*的组合路径规划算法。最后,仿真实验结果证明了本文所设计组合路径规划算法的可行性和有效性。
1 JPS 算法简介
JPS 算法是一种启发式路径规划算法,它保留了A*算法的基本结构,其不同点在于搜索路径过程中对后继节点拓展策略。相比于A*算法,JPS算法并非直接获取当前节点的所有非关闭的可达邻居节点作为后继节点,而是根据当前节点的方向和强迫邻居修剪规则确定后继节点的拓展策略,通过裁减无意义的节点及保留特殊节点,提高全局路径搜索的效率。
1.1 跳点筛选规则
根据节点周围是否存在障碍物,JPS 算法的跳点筛选规则分为两种情况:自然邻居筛选规则和强制邻居筛选规则。
1.1.1 自然邻居筛选规则
在图1 所示的栅格地图中,灰色栅格表示可裁减节点。假设路径搜索到了节点x处,该节点的父节点为p(x),p(x) 到x的方向为扩展节点的当前方向。图1 为自然邻居的筛选规则,主要有直线方向和对角线方向的筛选方式。

图1 自然邻居筛选规则
如图1(a)所示,父节点p(x) 到x为水平方向,故此时x的扩展方向为直线方向。若p(x) 要到达节点n,虚线和实线的路径代价相同,即p(x) 可以不经过节点x到达节点n且代价不会增加,则称n为可裁减节点。根据以上规则,除了白色节点q之外的其他节点均可被裁减,则称节点q为节点x的自然邻居。
如图1(b)所示,x的扩展方向为对角线方向,p(x) 不经过节点x到达n的路径最短(图中虚线所示为最短路径)。同样的,白色节点为自然邻居,其他节点均可被裁减。
1.1.2 强制邻居筛选规则
强制邻居筛选规则如图2 所示,黑色栅格为障碍物,其他均为可行走节点。不管当前方向为直线方向还是对角线方向,均不存在任何一条路径使得p(x) 到n不经过节点x为最短路径,即图中的实线为最短路径,则定义n为x的强制邻居,x为n的跳点。

图2 强制邻居筛选规则
1.2 评价函数
JPS 算法寻路时,对每一个加入open 列表中的跳点进行评估,选择代价最小的跳点作为下一父节点,通过不断地迭代直到扩展到目标点。JPS 算法的评价函数如式(1)所示。

式中,f(n) 为从起始节点经过当前节点n到目标节点的评价函数,g(n) 是起始节点到节点n的实际代价函数,h(n) 为当前节点n到目标节点的最小代价函数。
在二维空间中,一般采用欧式距离计算g(n),即:

式中,(X(n),Y(n)) 为当前跳点n的位置,(X(n-1),Y(n -1)) 为上一跳点的位置。
对于h(n) 而言,常见最小代价函数的计算方式有曼哈顿距离、切比雪夫距离和欧式距离[8],本文采取欧氏距离计算h(n),即:

式中,(X(n +1),Y(n +1)) 为目标节点的位置。
1.3 JPS 算法寻路
图3 为JPS 算法的寻路过程,其中S为起始点,D为目标点,阴影栅格为筛选后留下的跳点。起始点S的当前方向为空,则沿着8 个方向扩展搜索跳点。从S出发只有下、右、右下3 个方向可走,但向右搜索遇到边界,向下搜索至障碍物,右下方向搜索到跳点M。将M作扩展节点继续搜索,M的当前方向为对角线方向,但此时可走的方向只有向右,向右搜索到跳点W。节点W的当前方向为水平方向,沿右、右下2 个方向搜索到跳点V。节点V沿着当前方向搜索到L,L继续搜索直至目标点D,顺着父节点回溯到起始点便得到了最终路径。
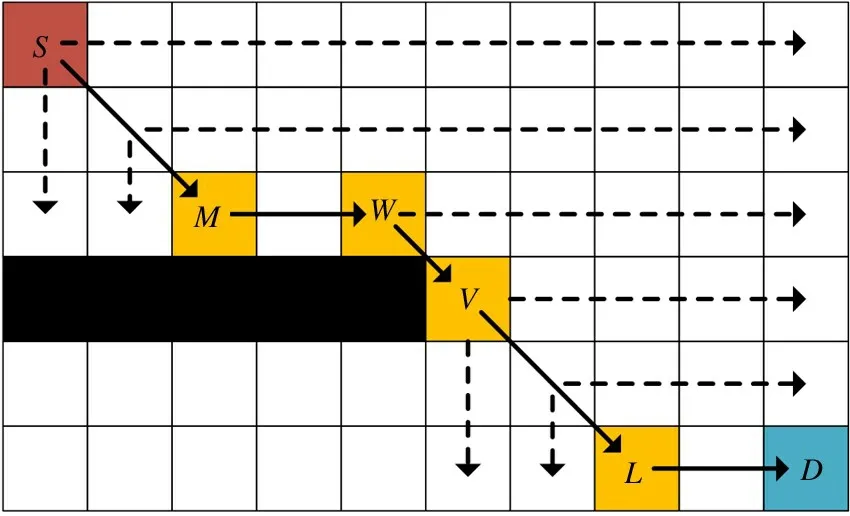
图3 JPS 算法寻路过程
2 改进JPS 算法的设计
在路径搜索的过程中,JPS 算法可优化A*算法寻找后继节点的操作,它是根据当前节点的方向和邻居节点的特性跳过其他多余的节点,由此省略了重复多余的计算过程。然而,JPS 算法所规划路径往往过于靠近障碍物,易产生碰撞甚至横穿障碍物的情况,从而影响路径的安全性;其次,当大规模地图中存在不对称的情况时,JPS 算法会找到过多的跳点,同时也会不断地操作open 列表和close 列表中的节点,导致路径搜索效率降低。针对移动机器人在对角线穿越障碍物时,可能会发生一定的碰撞而影响寻路过程中的安全性,本文通过修改冗余节点删减规则和跳点筛选规则,改善JPS 算法路径寻优的性能。
2.1 冗余跳点的删除
JPS 算法中跳点可以分为两种:至少有一个强迫邻居的跳点和没有强迫邻居的跳点[9]。前一种类型的跳点至少相邻一个障碍物,并且它们在两个不相邻的节点之间至少有一条最佳路径。如果删除这些跳点,很有可能导致算法不能返回最优路径。而后一种类型的跳点不与任何障碍物相邻,即中间跳点,该跳点只作为转折节点,最优路径选择时可以改变方向,到达前一种跳点或者目标节点。
因此,中间跳点是可以安全修剪的,并且不会影响算法的最优性。如图4 所示,数字1、4、6 为中间跳点,其他黑色数字为至少有一个强迫邻居的跳点。每个中间跳点最多有3 个后继节点:第1 种是水平可达的跳点,第2 种是垂直可达的跳点,第3 种是不改变方向的情况下可以到达下一个中间跳点。当修剪中间跳点时,将它的后继跳点存储在一个列表中,并用该后继者代替中间跳点,将这个过程不断递归,直至删除所有中间跳点。
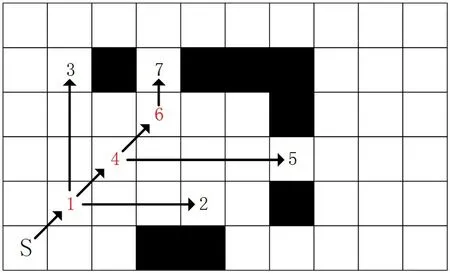
图4 修剪中间跳点
2.2 跳点筛选规则的改进
改进的跳点筛选规则如图5 所示。跳点筛选分直线和对角线方向,邻节点裁减规则不变。直线方向上改进的跳点筛选规则如图5(a)所示,节点n是x的强制邻居,当邻节点存在障碍物时,改进算法是不允许对角线穿过障碍物到达强制邻居。故从p(x) 到达节点n是必须经过节点x、y的,此时将x视作普通节点,将节点y视为跳点进行规划。
图5(b)是对角线方向上改进的跳点筛选规则,若不能以对角线穿过障碍物,p(x) 必须经过节点y、x、z才能到达节点n,此时将x视为普通节点,y和z当做跳点。
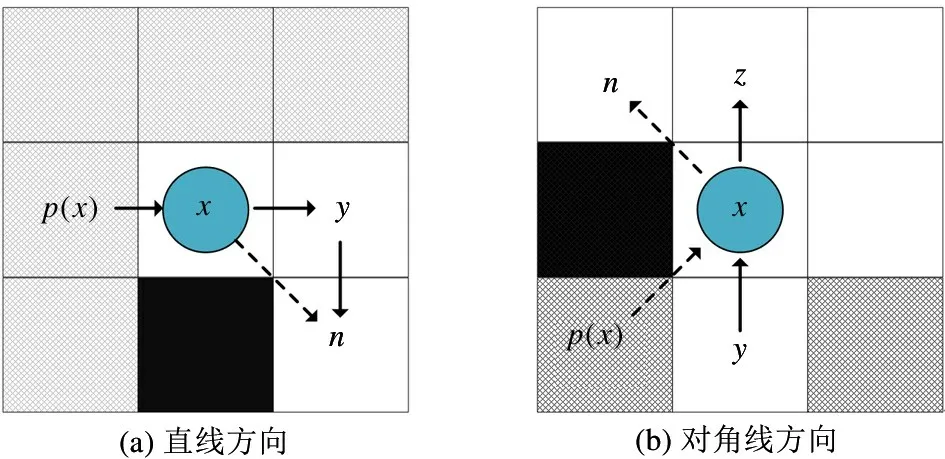
图5 改进跳点筛选规则
2.3 安全性评估模型设计
为了评估所搜寻跳点的安全性,在JPS 算法中引入安全性评估函数对求解路径的安全性进行评估。本文采用二维高斯模型构建跳点安全性评估模型,包括平均碰撞度和碰撞度函数,分别如式(4)、(5)所示。

FT为平均碰撞度,O为影响范围内障碍物的个数,I为求解路径的节点个数。T为碰撞度函数,(xi,yi) 和(xo,yo) 分别是路径节点坐标和障碍物坐标,ρ((xi,yi),(xo,yo)) 是路径当前节点到最近障碍物的距离,do是障碍物影响范围,与机器人本身的模型有关,α、β决定碰撞对机器人造成危险的程度,由机器人的速率以及障碍物的材质决定。
3 改进JPS 和A*组合路径规划算法
JPS 算法不是从相邻节点中选择下一个节点,而是跳过大量可能会添加到open 列表和close 列表中的中间节点,旨在消除路径间的对称性,提高搜索效率[10]。但是,当寻路过程中存在障碍物稠密区域且存在非对称路径时,相比于A*算法只需要从open 列表中选择具有最小代价函数值的节点,JPS算法每生成一个节点就需要寻找一个跳跃点,对于下一个节点的选择过程需要更多处理时间,此时,JPS 算法的寻路代价大,且规划的路径存在一定的安全隐患。因此,本文将所设计的改进JPS 算法与A*相结合,根据由地图环境的复杂度信息确定的跳点阈值函数选择不同的路径搜索规则。通过组合路径规划算法,一方面利用改进JPS 算法裁减掉对称路径搜索过程中的无意义节点,减少节点扩展的数量;另一方面基于A*算法有效避免复杂路径搜索过程中存在的安全隐患,提高路径搜索效率。
3.1 跳点阈值函数的设计
JPS 算法寻路时,环境中的障碍物越混乱,扩展的跳点数量越多,搜索效率越低。因此,设计了直通率Pe和障碍率Po判断地图环境的复杂程度。

式(6)中,ne为一行或一列均为无障碍栅格的条数,R和C为环境地图的行数和列 数。Pe值越大,环境的混乱程度越低。式(7)中,no为地图中障碍物栅格的数量,N为地图总栅格的数量。
环境的复杂程度直接影响跳点数量,从而影响路径搜索的效率。将路径搜索一定区域内跳点数量进行量化,记为K,则有

式中,U表示当前节点的搜索范围,K表示搜索范围U内跳点数量。
跳点阈值与直通率Pe和障碍率Po有关,地图环境越复杂,跳点就越多。因此,根据环境地图的复杂度,由式(6)和式(7)定义跳点阈值λ为

因此,改进JPS+A*组合规划算法的切换条件为:当K≥λ时,由改进JPS 算法切换为A*算法搜索。
3.2 改进JPS+A*组合规划算法流程
基于式(9)所定义的跳点阈值函数,将所设计的改进JPS 与A*算法相结合,构成组合规划算法,即当跳点数量较少时,采用JPS 算法规划以便快速穿过对称路径,避免不必要节点的扩展;当跳点数量过多时,便转换为A*算法进行路径规划,安全且高效通过障碍物稠密的地图环境,由此构成一条完整的规划路径。改进JPS +A*组合规划算法流程图如图6 所示。

图6 改进JPS+A*组合规划算法流程图
3.3 组合规划算法步骤
设置搜索open 列表和close 列表,起始点为S,目标点为D。改进JPS+A*的组合规划算法步骤如下。
步骤1初始化,判断起点与终点是否在同一连通区,若不在,搜索失败退出。
步骤2计算地图的直通率Pe和障碍率Po,根据式(9)得到该地图的跳点阈值λ。
步骤3将起点S加入到open 列表中。
步骤4将open 列表中f(n) 值最小的节点i取出,并将其加入到close 列表中。若i=D,沿着父节点回溯得到路径,转到步骤10;若不是,扩展节点i。
步骤5判断当前节点i搜索范围内跳点数量K(基于式(8)),比较K、λ,若K <λ,转到步骤6;否则转到步骤7。
步骤6改进JPS 算法搜索一步,寻找不在close 列表中跳点。
步骤7A*算法搜索一步,沿8 个方向寻找当前节点不在close 列表中的可达邻节点。
步骤8判断该节点是否在open 列表中,若不在,将该节点加入到open 列表中;若在,计算该节点g(n) 和父节点的判断更新。
步骤9转到步骤4。
步骤10基于式(4)、(5),通过安全评估模型计算所得路径的平均碰撞度,寻路成功。
4 仿真及实验验证
环境建模是建立一个供移动机器人自主移动的场所,对环境模型的要求是便于机器人控制器存储、处理、更新和使用。因此本文选择了存储简单且易于实现的栅格法构建地图,并建立安全性评估模型对路径安全性进行评估,式(5)中参数取α=1,β=3。
首先,建立15 m×15 m 的移动机器人工作地图环境,将本文算法改进的JPS 算法与A*算法和JPS算法进行仿真测试。然后,扩大地图规模,建立20 m×20 m 和30 m×30 m 的地图模型,将改进的JPS +A*算法与JPS 算法作仿真实验,验证组合算法的合理性。最后,在50 m ×50 m 的地图模型中,将改进JPS+A*算法与改进JPS 算法比较,验证随着地图规模的增大,组合规划算法在路径搜索时间及路径长度等方面的优势。
4.1 实验1
在15 m ×15 m 的地图环境下,基于A*算法、JPS 算法和本文所设计的改进JPS 算法的路径规划结果如图7 所示,其中阴影栅格为扩展节点。3 种算法的实验路径参数如表1 所示。
对于规模较小且障碍物较少的地图环境,比较图7(a)、(b)可知,相比于A*算法,JPS 算法快速穿越对称路径,扩展节点相比A*算法大大减少。由表1 的实验数据可知,当路径长度相同的情况下,JPS 算法较A*算法,移动时间缩短了47.16 ms;而改进JPS 算法与JPS 算法相比,路径长度缩短了5.01%,移动时间减少了16.63%,且由于对跳点筛选规则的改进,路径的平均碰撞度降低了40.00%。综合上述分析,所设计的改进JPS 算法提高了搜索效率和路径安全性。

表1 路径规划参数表

图7 基于15 m×15 m 栅格地图的3 种算法路径规划结果
4.2 实验2
为了验证本文改进JPS +A*算法在复杂环境的地图中的合理性,将地图规模扩大为20 m ×20 m和30 m×30 m,基于JPS 算法、A*算法和改进JPS+A*算法仿真结果如图8 和图9 所示。

图8 20 m×20 m 栅格地图中不同算法的路径规划

图9 30 m×30 m 栅格地图中不同算法的路径规划
由图8 和图9 椭圆标记区域可知,在穿越障碍物稠密的环境时,改进JPS+A*算法相较于JPS 算法规划的路径更平滑且更合理。由表2 可得,在路径长度和移动时间上,改进JPS+A*算法较传统A*和JPS 算法具有较大的优势;且栅格地图的规模越大,改进JPS +A*算法的搜索效率提升越明显。在路径安全性上,改进JPS+A*算法的平均碰撞度远小于其他两种算法且所规划的路径更加合理。由上述分析可知,本文改进的组合规划算法适用于规模较大、对移动机器人的安全性要求较高的环境。
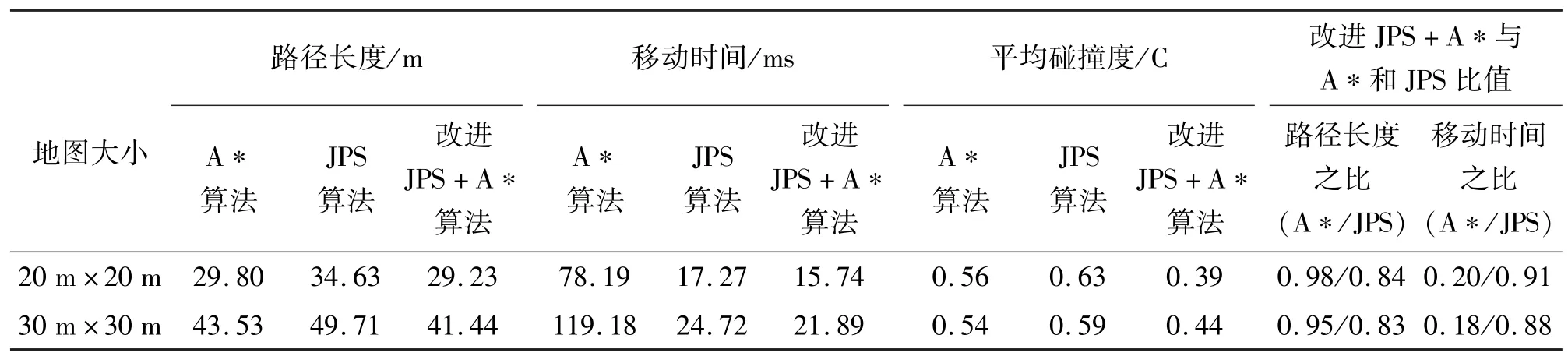
表2 不同规模地图中各算法的路径规划参数表
4.3 实验3
将地图规模进一步扩大为50 m ×50 m。基于改进JPS +A*的组合路径规划算法和改进JPS 算法的规划结果如图10 所示。

图10 本文算法与改进JPS 算法的路径规划结果
由图10 中椭圆标记区域可得,当改进的JPS 与A*算法相结合后,利用A*算法有效处理复杂非对称路径。由表3 实验数据可知,JPS +A*组合路径规划算法规划出的路径长度比改进JPS 算法减少了0.91 m,移动时间缩短了23.11%,路径搜索效率显著提高。

表3 路径规划参数表
5 结论
本文设计了一种基于改进JPS +A*的组合路径规划算法。该算法针对JPS 算法内部运算机制及复杂地图环境因素对移动机器人路径寻优效率影响的问题,通过删除冗余中间跳点、改进跳点筛选规则及建立安全性评估模型实现了一种改进的JPS 算法;在此基础上,根据环境的复杂度设计了跳点阈值函数,将所设计的改进JPS 算法与A*算法相结合,实现了复杂地图环境下的路径寻优且提高路径搜索的效率。仿真实验结果表明,相比于传统的JPS 算法,本文所设计的改进JPS+A*组和路径规划算法更适用于复杂地图环境,尤其是存在非对称路径的地图环境,有效地减少了节点数量、移动时间和平均碰撞度,提高了移动机器人的安全性和工作效率。后续工作将进一步改善算法的避障能力和求解路径的平滑性。
