基于三维连续-离散耦合方法在边坡稳定中的应用

2022-06-17熊鑫，黄鹤

港工技术 2022年3期

熊鑫，黄鹤

（中交第二公路勘察设计研究院有限公司，湖北武汉 430052）

引言

随着山区高速公路的快速发展，尤其是在复杂地质条件下的西南山区，挡土墙在土基支护和边坡支护工程中的应用越来越广泛，其在保障路基边坡稳定性中扮演重要角色[1]。研究其力学性质和稳定性，进而提出合理的加固方案，是保障高速公路安全运营的重要前提。

针对边坡挡土墙的破坏机理，许多学者采用数值模拟的方法进行了全面的探索。金爱兵等[2]采用FlAC 分析了路面动载荷下挡土墙的力学响应和墙体内部破坏机制，并提出了预应力锚杆加表面喷浆的支护措施；张俊腾等[3]采用Plaxis 有限元软件探讨了软土地基加筋挡土墙的破坏模式，其破坏模式取决于筋土组合体和地基土的相对稳定性；OmidRezaBarani 等[4]提出了一种零厚度接触面元的有限元模拟方法，考虑墙后土体剪切带的影响，提高了对墙体性能的预测。陈国舟等[5]基于离散元软件模拟了考虑结构-土体摩擦作用下桶形挡土墙主动土压力的分布规律；冯振[6]和孟云伟等[7]采用颗粒流软件对石笼挡土墙施工过程中的细观力学进行了模拟研究，从细观角度分析了挡土墙的破坏机理。但是基于工程尺度建模的有限元分析无法反映挡土墙破坏的微观机制，而受计算效率制约的离散元软件又避免不了尺寸效应的问题。

连续-离散耦合技术不仅可以延续连续介质力学在模拟大尺寸岩体变形和局部破坏计算效率高的优点，而且还可以从细观尺度上对关键部位精细化模拟其破裂行为，既能满足计算效率要求，又不受变形量限制，具有重要的理论意义和实用价值[8-9]。本文将三维连续-离散耦合方法应用于路基边坡支护挡土墙的变形细观分析，基于有限差分法理论和颗粒离散元理论，以依托工程为背景建立路基边坡连续-离散三维数值模型，对比挡土墙的宏细观力学响应，提出优化加固方案，对路基边坡支护方案设计具有一定参考价值。

1 三维连续-离散耦合技术原理

基于边界控制墙体的三维连续-离散耦合方法是通过边界墙体来实现连续域和离散域之间的数据交换，边界墙体由三角形单元面组成，三角形顶点依附在连续域的单元节点上，耦合示意图见图一。当颗粒与墙面接触时，采用重心插值法将接触力、平动刚度以及力矩外推到三角形面顶点（即连续域的节点），再由连续域的运动平衡方程获得速度和位移。连续域在经过边界墙体将速度和位移传递给离散域颗粒，并重新定义颗粒与墙体的接触位置，图2 展示了离散颗粒与连续单元力传递的过程[10]。

图1 离散颗粒与连续单元耦合示意图

图2 离散颗粒与连续单元力传递示意图

耦合的核心问题是宏细观参数的一致性标定，因耦合程序中没有材料的本构模型和宏观岩体力学参数概念，保证离散颗粒集合体和连续模型的宏观属性一致是细观分析的前提[11]。因此，以宏观模型的力学行为为基准反复调试实验室模型来标定计算的细观参数。

2 三维连续-离散耦合模型构建

2.1 模型搭建

本文以西南山区某高速公路路基边坡为依托，边坡主体为碎石土，基底为强风化花岗岩，初步拟采用挡土墙支护，衬砌采用70 cm 厚的 C30 混凝土，根据《混凝土结构设计规范》（GB50010-2010），混凝土弹性模量E=30 000 MPa。根据地质资料显示，没有明显的断层分布，也不考虑渗流和动力荷载的影响，因此考虑采用Mohr-Coulomb 弹塑性模型，分别采用实体单元和颗粒体模拟挡土墙。由于本文重点关注滑坡过程中挡土墙失稳机理，故研究对象是挡土墙及墙后土体，参照《公路路基设计规范》（JTGD30-2015）选取路基工作范围，由于路基刚度较大且开挖较浅，忽略了开挖步的影响，路基模型图进行了相应简化，见图3，相关力学参数见表1。

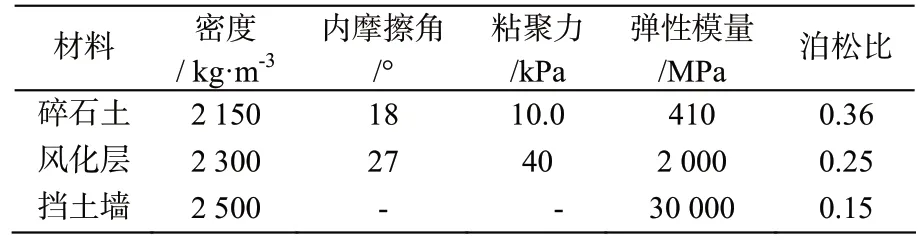
表1 连续域力学参数

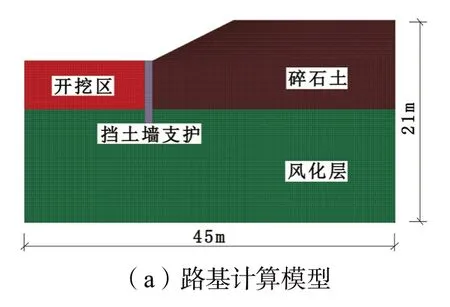
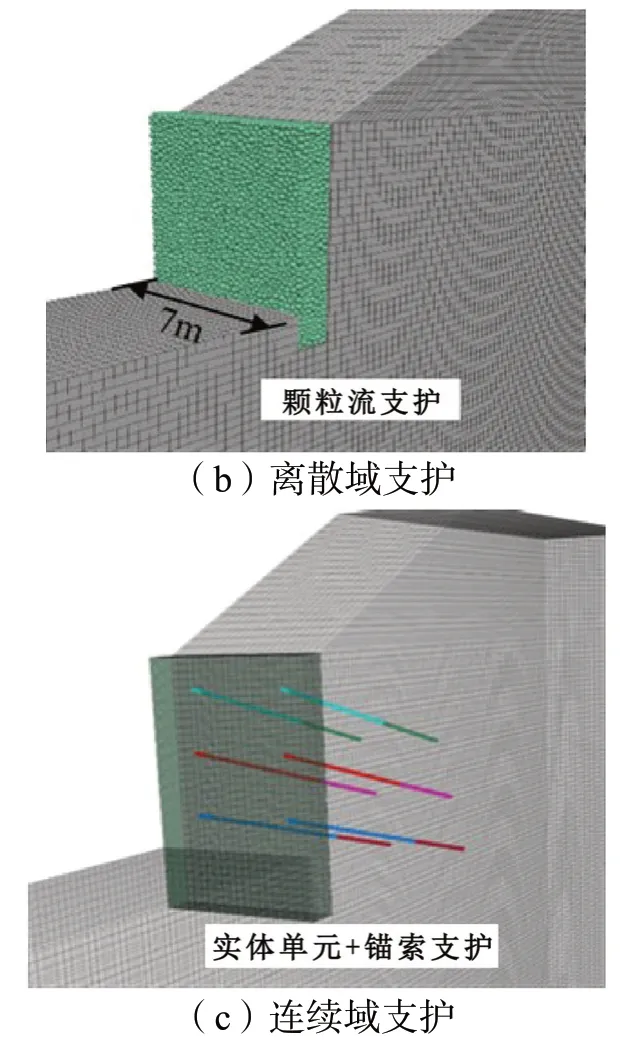
图3 计算模型及支护图

边坡模型由实体单元进行模拟，衬砌挡墙采用离散元。考虑到计算的收敛效率，用约1.1 万个独立的球形散颗粒填充尺寸为 0.7 m×7 m×6 m 的挡土墙区域，离散颗粒直径范围为0.05～0.1 m，离散域采用平行粘结模型，此模型对水泥间骨料的粘结行为有很好的模拟效果[11]。离散颗粒细观参数标定流程为：以边坡围岩和衬砌模型的宏观属性为基准，对细观参数反复调试，即路基开挖后，采用连续的桩单元作为挡土墙或离散颗粒填充作为挡土墙，其衬砌结构和周边围岩的力学行为（力和位移）要保持一致。最后标定的细观参数见表2。

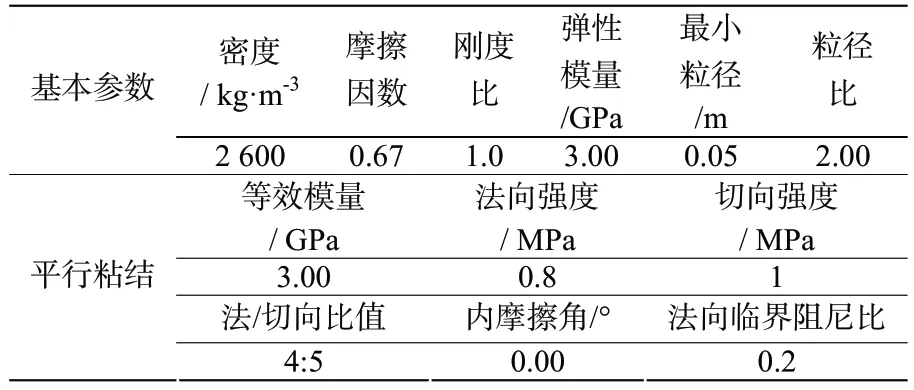
表2 离散颗粒的细观力学参数

2.2 模拟步骤及边界条件

三维连续-离散耦合挡土墙模拟的顺序为：首先初始应力场通过连续模型自重应力加载模式生成，其次通过连续域null命令开挖掉路基和支护区域单元，固定单元速度并生成颗粒挡土墙，并赋予强度。最后计算平衡时间步，由此获得路基边坡和挡土墙相关应力、应变计算结果[12]。

耦合模型的边界条件包括连续域边界、离散域边界以及耦合域边界，连续域边界延用一般的固定模式：固定四周和底部边界，耦合域边界在一致性检验时采取应力边界，通过应力加载方式获得[13]，离散域边界在一致性检验时固定了前后颗粒的法向速度。

2.3 一致性检验

耦合模型中离散颗粒的细观参数一旦确定，它的宏观表现是唯一的[14]，如果离散域和连续域的位移场和应力场能够保持连续性，就说明满足一致性检验，即离散元模型细观参数的选取能真实再现岩土体的强度和变形特性。本次耦合模型选取开挖后不支护情况下离散域岩土体材料的破坏是否逼近实际岩体真实行为，作为一致性检验的算例。

由图4可以看出，耦合区域连续模型和离散模型的位移云图颜色变化和数值大小吻合较好，颗粒的运移方向和滑坡体方向也高度一致，证明了耦合模型位移场的连续性和一致性。分析图5，最大主应力的分布与一般滑坡体的应力分布一致，拉应力多集中在模型上部且滑坡体附近较集中，颗粒填充域两侧的主应力分布从颜色分布上看也是连续的，说明耦合模型能够较好的实现应力的传递，且符合连续域工程开挖一般应力分布。综合分析，通过对离散颗粒细观参数的反复调试和标定能够使离散域数值模型的宏观力学行为（位移和应力）和连续域保持一致性，此细观参数的标定方法是可行的。

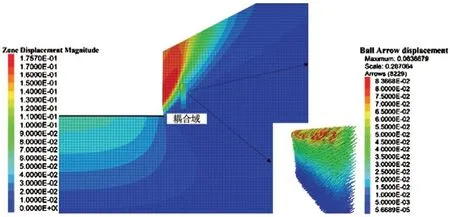
图4 路基开挖后无支护位移对照云图

图5 路基开挖后最大主应力分布云图

3 支护结构受力机理分析

3.1 挡土墙受力机理分析

图6 为单一挡墙支护边坡开挖运行一定时步的整体位移云图、颗粒挡土墙支护位移以及颗粒挡土墙的接触力链图。选取实验室标定的C30 混凝土模量，对比图4 和图6，边坡开挖后不支护情况下的最大位移为17.5 cm，挡土墙支护后的位移为3.5 cm，参照《公路挡土墙设计与施工技术细则》要求，单一挡墙并没有对路基边坡起到足够的支护效果，颗粒挡土墙最大位移约为6 cm 时材料已逐渐发生脆性破坏，最大位移出现在挡土墙上部，越往下位移值越小。接触力链图显示，破坏前挡土墙处于上部受拉下部受压的应力状态，且拉应力有逐渐向下扩展的趋势。

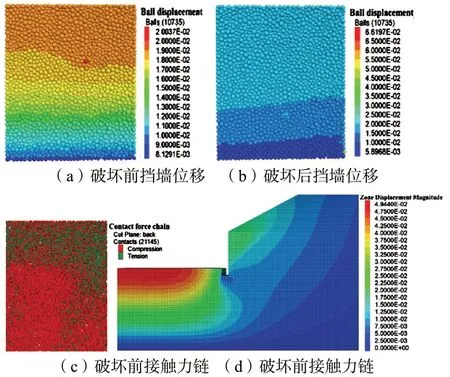
图6 开挖后连续和离散支护位移增量对照及力链图

将三维连续-离散耦合技术应用于工程岩体开挖支护最终目的是发挥离散元的优势，即表征支护材料在施工过程中或服务年限内由外力原因可能造成的弹塑性变形或破裂现象。分析其破裂机理，明确拉剪破坏次序和位置，采取相应的加强支护措施：锚索、加筋挡土墙等。

图7 为不同时步下随着边坡滑坡塑性区的逐渐贯通挡土墙的破坏形式及破坏位置，由图显示滑坡初期挡土墙中部偏下的位置率先出现拉裂纹，挡土墙整体强度下降；随着平衡时步的逐渐增加，边坡整体滑移面逐渐形成，此时挡土墙剪裂纹迅速贯通，挡土墙发生冲剪破坏。表明边坡逐渐失稳的宏观现象与挡土墙材料同步破坏细观现象保持较好的一致性。

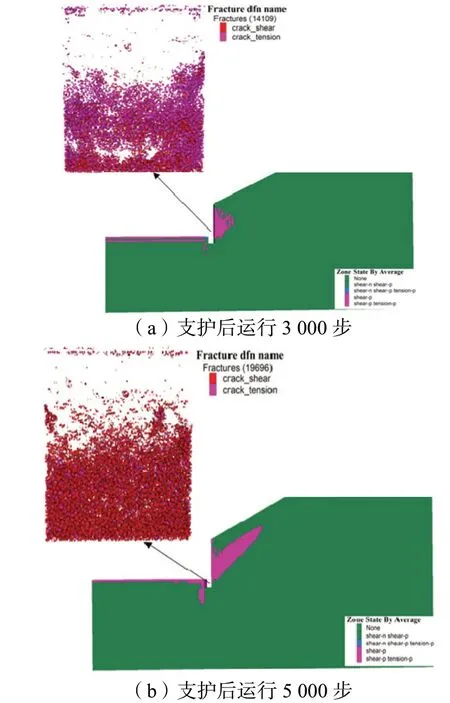
图7 边坡失稳塑性指标及挡土墙细观破裂对照图

3.2 支护方案优化

根据上述细观分析后挡土墙破坏形式和破裂的位置，从而确定优化支护的方式和强度。无加固措施情况下挡土墙上部处于拉应力状态，挡土墙的破坏形式为首先是细小拉裂纹的产生造成挡土墙整体强度下降，最后发生冲剪破坏，破坏的位置大致在挡墙中部偏上。重点对挡墙上部进行了锚索支护，缓解其处于拉应力的不利状态，提高其抵抗侧向位移的能力，避免拉裂纹的产生。采取三排预应力锚索进行支护，最后一排锚索下穿过冲剪破坏位置。总长度分别为10 m、11 m 和12 m，锚固长度均取4 m，与水平面夹角均为20°，预应力从上到下分别为55 t、60 t、65 t。

从图8 可以看出，加密锚索优化方案后对边坡支护取得了很好的效果，颗粒挡土墙和实体单元挡土墙的位移分布和大小基本一致，实体单元挡墙最大位移为12.7 mm，颗粒体挡土墙最大位移为12.2 mm。接触力链图显示，锚索支护后大大缓解了挡土墙上部受拉的不利情况，使挡墙整体处于受压状态。图9 中依次展示了开挖后锚索的轴力以及挡土墙水平土压力，从图中可以看出，锚索预应力已被成功施加在挡墙上，水平土压力的模拟值和理论值变化趋势也基本相近。