某型航空发动机减速单元体机匣热—结构耦合分析
2022-06-17邹闰丁琪马洪亮唐家茂陈蔚兴罗岸
邹闰,丁琪,马洪亮,唐家茂,陈蔚兴,罗岸
1.中南大学机电工程学院,湖南长沙,410012;2.陆军装备部航空军事代表局驻株洲地区航空军事代表室,湖南株洲,412002;3.中国航发南方,湖南株洲,412002
0 引言
随着我国国民经济的快速发展和低空空域逐步开放等相关利好政策的出台,国内对直升机的需求越来越大[1],航空发动机是飞机飞行的动力来源,发动机状态的好坏将直接影响飞机的性能。其中,减速单元体是航空发动机的关键部件之一,其可靠性将直接影响到直升机的运行安全性。
本文以某型航空发动机减速单元体为研究对象,该减速单元体为两级斜齿轮减速装置,将自由涡轮的功率传递给发动机功率输出轴,与此同时,由于该单元体除了减速作用,还具有测扭功能,在发动机工作状态中通过测量中间齿轮轴向力,实时测量真实输出扭矩,因此对齿轮的位置精度与啮合状态有着严格要求。机匣部分是减速单元体的重要部件,采用高性能耐热铝铜合金ZL208材料。它在热源作用下的热变形直接影响了轴承孔的位置精度,进而影响齿轮啮合状态和传动精度,对测扭机构有着重要影响。但由于单元体结构和热源分布较为复杂,热变形对扭矩测量的影响尚未明确。所以,探究减速单元体机匣的热变形误差就显得十分重要。
近些年来,国内外研究人员针对减速齿轮箱的热特性展开了一系列的研究,也取得了相应的研究成果。目前,关于齿轮箱的热分析方法主要有热网络法[2-3]、有限差分法[4]、有限元法[5-6]等。但热网络法只能获得关键节点的温度,不能对整体温度分布进行计算,对于复杂对象,有限差分法则效率较为低下。而有限元法发展较为成熟,能对大型结构整体进行较为精确的计算,因此应用广泛。Patier等人[7]采用有限元法对圆柱齿轮在热平衡状态下的稳态温度场进行了求解,并分析了齿轮温度分布的影响因素。张小蝉[8]以某风力发电机组减速箱为研究对象,利用集总参数法建立了减速箱稳态热平衡模型,并同时使用Matlab和ANSYS进行求解验证结果准确性,将结果导入ANSYS中进行热结构耦合分析,得到减速箱热变形具体数值。汝艳[9]通过有限元法对齿轮在不同环境温度和不同传递扭矩的条件下齿轮本体的温度分布进行了分析。葛世祥[10]通过ANSYS Workbench对满载工况下的高速齿轮箱进行热-结构耦合分析,计算齿轮箱的变形值,并分析其对齿轮啮合的影响。
本文运用ANSYS Workbench对减速单元体进行有限元仿真,通过对减速单元体工作过程热源进行分析,计算各热源发热功率和边界条件,进行稳态温度场仿真分析得到机匣平衡状态下温度分布状态。相对于直接耦合,对于一般的线性耦合来说,采用间接耦合法更为灵活、方便。因此,采用间接耦合法进行热-结构耦合分析,得到减速单元体机匣热变形结果,计算轴承孔平均变形值,分析轴承孔变形对齿轮轴线平行度偏差的影响,并将其量化为对齿轮啮合状态的影响,进而分析热变形对扭矩测量的影响。
1 减速单元体三维建模及热源分析
图1为某型航空发动机减速单元体三维模型,该减速器两级均采用斜齿轮传动,其主要技术参数如表1所示。
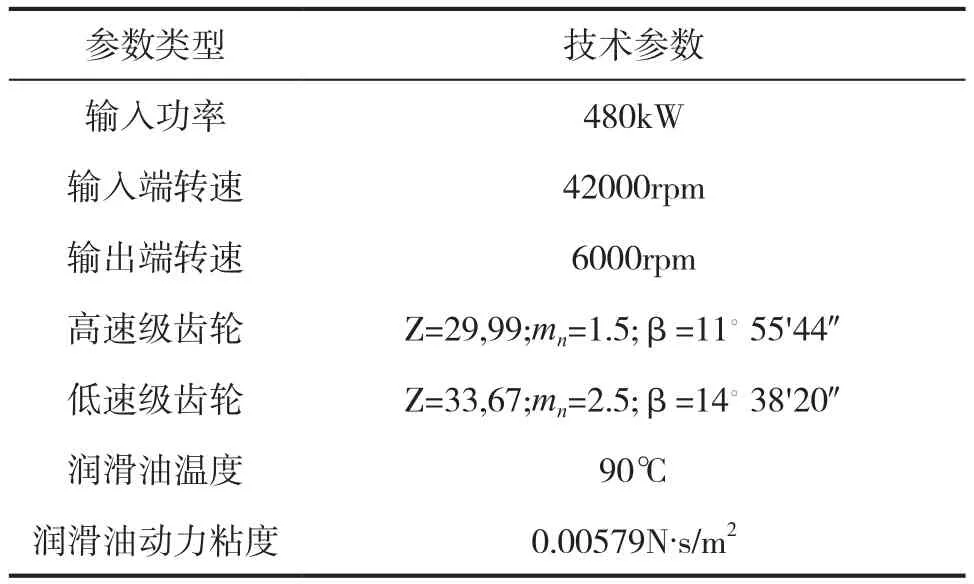
表1 减速单元体技术参数
在发动机工作运转过程中,减速单元体中齿轮和轴承高速旋转,其中的众多摩擦副造成功率损失,并绝大部分转化为热量,一部分热量由单元体内油气混合物带走,一部分热量传导至单元体其他部件。通过对单元体内部结构和工作原理进行分析,可将单元体主要内部热源分为以下几部分:
(1)高速旋转轴承滚子与轴承内圈或轴颈跑道滚动摩擦;
(2)高速旋转轴承滚子与轴承外圈滚动摩擦;
(3)斜齿轮啮合时齿面的滑动和滚动摩擦;
(4)齿轮轮齿对箱内油气混合物搅动的搅油损失。
2 热载荷计算
2.1 轴承发热功率计算
滚动轴承在整个运转过程中产生的摩擦力矩受多种随机因素的影响,具有波动性[11]。综合轴承摩擦力矩的特点,可使用滚动轴承在运行平稳状态下的平均摩擦力矩进行轴承发热量计算。Palmgren[12]经大量实验和验证,得出了轴承摩擦力矩计算的经验公式,公式如下:
确定减速单元体各轴承的摩擦力矩后,可计算出由于轴承摩擦生热而导致的功率损失。轴承的发热功率计算公式如下:
减速单元体各轴承摩擦力矩和发热量计算结果如表2所示。

表2 减速单元体各轴承摩擦力矩和发热量
对于滚动轴承,对其发热功率分配时,可将热量均分至滚动体与滚道。轴承整体的热量1/4传递至内外滚道,1/2传递到滚动体。
2.2 齿轮副发热功率计算
(1)齿面啮合摩擦损失。齿轮啮合摩擦主要包括齿面滑动摩擦、滚动摩擦和由于金属弹塑性变形导致的内摩擦力。其中内摩擦力相对于前两者可忽略,本文采用目前应用较为广泛的Anderson and Loewenthal法[13]计算齿轮产热功率。齿面滑动摩擦、滚动摩擦功率计算公式如下式:
(2)齿轮搅油损失。齿轮搅油损失受润滑油参数、齿轮转速、模数、压力角和螺旋角等参数影响,目前应用较广的斜齿轮搅油损失计算方法为AGMA6011-I03给出的经验公式[14],其将搅油损失分为轴颈、齿轮断面、齿轮表面三个部分,具体公式如下:
减速单元体各级齿轮副热功率损失计算结果如表3所示。
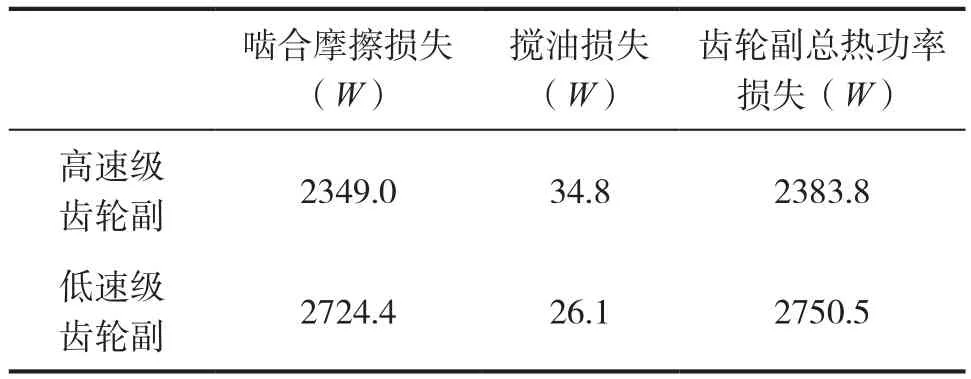
表3 各级齿轮副热功率损失
3 减速单元体稳态温度场分析
3.1 边界条件的确定
对单元体边界条件进行确定主要是计算热对流系数,根据传热学原理,单元体内存在的对流换热可分为两部分:一部分为机匣内壁面以及内部轴系零件表面与油气混合物的强制对流,一部分为机匣外壁面与空气的自然对流。
通过油气混合物的普朗特数、热传导率和运动粘度计算传热介质的努塞尔数和雷诺数。因此可计算出各对流面换热系数如表4所示:

表4 对流面换热系数
3.2 单元体稳态温度场仿真结果与分析
根据计算得到的轴承与齿轮发热功率值,施加热流量载荷到轴承滚子、轴承内外圈跑道和齿轮表面,并对轴系零件以及机匣内壁面定义与油气混合物的强制对流系数、在机匣外壁面定义与空气的自然对流换热系数。进行求解得到机匣稳态温度场分布云图。
由图2可看出,单元体机匣低速级温度明显低于高速级温度,原因是低速轴承转速低,生热量少。机匣温度自高速级向低速级递减,温度最高处为142.39℃,出现在高速级后轴承安装处,考虑是该轴承转速高,产热量大,且相比于高速级前轴承该处润滑油难以到达散热效果差,因此,此处热量积聚较其他位置严重。并且由于减速单元体在结构上为左右对称,局部差异较小,所以温度场在左右方向基本呈现对称分布,整体温度分布规律与实际试车测量值基本相符。
4 减速单元体热-结构耦合分析
机匣各部位由于温度场的分布差异引起各部分产生不同程度的热变形,而机匣轴承孔产生的变形将影响齿轮的传动精度,由此需对减速单元体机匣在热-结构耦合作用下的变形进行分析。将单元体温度场计算结果导入作为热载荷,设置单元体约束、轴承载荷和边界条件,进行求解得到单元体机匣整体热变形云图如图3。
由图3观察可知,减速单元体机匣整体变形较大,原因在于润滑油温度较高导致单元体整体温升较大,因此产生的热膨胀变形较大,最大变形处出现在高速级后轴承安装处顶部为0.612mm,是由温度场热载荷与结构载荷耦合作用的结果。
为探究轴承孔变形对轴线平行度及其对齿轮齿向啮合的影响,需对轴承孔变形值进行计算。首先对六个轴承孔表面节点变形量导出计算其平均值,表5为单元体机匣热-结构耦合分析下,轴承孔在三个方向上的变形量。

表5 轴承孔变形值
对于因轴承间隙、轴承孔变形以及其他空间误差因素导致的轴线平行度误差,不同的轴系布置方式有着不同的计算方式,根据此例中轴线布置方式,参考宋乐民[15]所总结的轴线平行度误差计算公式如下式:
垂直平面:
水平平面:
由上式可计算得出轴线在不同平面平行度误差如表6所示。

表6 不同平面上轴线平行度误差
齿轮各支点累计间隙由于轴线偏转方向不同,其累计误差绝对值可能叠加或补偿,根据宋乐民总结的分类计算公式,换算可得由于轴线平行度误差导致的齿轮齿向啮合误差如表7所示。

表7 齿轮齿向啮合误差
高、低速传动齿轮均为5级精度,结合齿轮分度圆直径和齿宽,查阅齿轮手册得到齿轮螺旋线偏差为8.5,因此由于热变形导致的高、低速齿轮齿向啮合误差相比于螺旋线偏差分别为32.3%、28.31%。在现行设计中,此误差对于齿轮啮合产生的轴向力影响较小,因此对发动机扭矩测量影响也较小。
5 结语
基于ANSYS Workbench通过对减速单元体整体进行温度场有限元分析,获得了单元体机匣稳态温度分布,与实际工作状态下机匣状态温度分布规律相符。结合温度场计算结果,对单元体进行了热-结构耦合分析,获得了单元体机匣热变形结果,通过对变形云图分析可知,最大变形值出现于高速级后轴承安装处,且通过对6个轴承孔在不同平面变形量进行分析,将其转化为轴线平行度的影响,齿轮轴线的平行度误差对齿向啮合误差的影响为齿轮螺旋线公差的32.3%、28.31%,由此说明,热变形对中间齿轮轴向力影响较小,因此对发动机扭矩测量影响也较小,不是造成测扭机构故障的主要原因。此分析也为发动机在不同工况下对减速单元体热特性进行快速分析奠定了基础。
