寡头企业两周期以旧换新均衡模型及定价策略
2022-06-17李辉中尹译稀
李辉中, 尹译稀, 庞 琪, 吴 鹏
(1.四川大学商学院, 成都 610064; 2.武警警官学院, 成都 610213; 3.上海第一财经数据科技有限公司, 上海 200041)
1 引 言
随着制造产业闭环供应链的进步与完善,以旧换新成为了闭环供应链中不可或缺的一环.诸如手机、汽车及动力电池、家用电器等产品纷纷加入到以旧换新的行列[1].人类社会对于环境保护重视程度的提升以及对废旧物料循环的推崇使得以旧换新愈加受到人们的追捧[2].更为重要的是,作为一种市场营销手段,以旧换新被认为是企业的一种价格歧视方式.这对吸引消费者购买,促进企业根据产品生命周期进行规划布局具有重要意义.以旧换新的相关研究对于管理决策者根据生产运营实际状况进行决策提供了相应的借鉴.
目前,涉及以旧换新的相关定价决策研究可以分为纵向供应链以旧换新定价决策和供应链横向竞争以旧换新定价决策.在纵向供应链方面,孙浩等[3]建立了基于市场细分的两周期再制造闭环供应链的决策模型.Cao等[1]对B2C平台在以旧换新模式下官方自营与第三方零售商之间进行以旧换新定价决策进行了比较.Genc等[4]在两阶段闭环供应链中引入受技术水平与价格共同影响的回收率探究以旧换新的效益.Rao等[5]考虑了市场中同时存在新旧产品的情况,构建了稳态均衡模型探讨企业是否推行以旧换新策略并且如何定价的问题.Savaskan等[6]构建模型探究不同的逆向供应链渠道结构的回收效益.Giovanni等[7]考虑一个两阶段闭环供应链博弈,并决定是独家管理回收产品还是将其外包给零售商或第三方服务提供商.Miao等[8]研究了3种不同的回收模式下的企业最优决策.Xiao等[9,10]通过探究消费者在以旧换新或是出售给二手市场的选择行为来设定最优的动态定价,但并未考虑到同一行业的寡头竞争企业以旧换新定价博弈.在供应链横向竞争方面,Ferguson等[11]研究了制造商在面对再制造产品市场上的竞争威胁时的回收策略.黄永等[12]探究了制造商竞争环境下基于产品生命周期的闭环供应链的定价和生产策略.林欣怡等[2]建立了两周期零售商竞争环境下的分散决策模型和集中决策模型,得到了最优定价和生产策略,并利用收益共享契约协调整个闭环供应链.卢荣花等[13]在零售商竞争环境下,建立两周期闭环供应链回收渠道决策模型.Zhu等[14]研究了在消费者市场规模处于变动的情形下,两阶段双寡头竞争模型中同质产品以旧换新数量竞争策略.
通过上述研究能够发现,以往的纵向供应链以旧换新研究聚焦于回收模型的变化探索,而供应链横向竞争研究则聚焦于竞争对供应链协调定价的变化,通常假设寡头企业产品为同质的.但实际生产生活中同类型不同质量水准的产品存在一定的竞争,这些研究缺乏对不同质量水准产品加入以旧换新竞争的探讨.本研究结合上述研究特点,设定在两周期内,同类型不同质量水准的产品双寡头生产商A与B,通过满足市场的消费者效用形成相应的市场划分,并设定以旧换新价格使得自身利润最大化的博弈模型,探讨以旧换新是如何影响企业间的横向竞争以及相应的销量、利润变化,寻求模型的均衡及现实意义.
2 模型介绍
考虑某一双寡头市场中的企业A与企业B生产同类型的竞争产品,其中企业A的产品比企业B的产品更为高端,即va>vb>0,同时为了简化分析,假定ca>cb=0.消费者在每一周期内只使用一件产品即可满足效用[8],而新购买的产品能够在两周期内都为消费者提供效用,第一周期产品为新产品,第二周期产品损耗为旧产品.两企业在两周期内决定实施以旧换新策略并依据利润进行博弈,在此基础上我们作如下假设:(1) 企业只换购本企业产品,并忽略回收处置旧产品产生的成本;(2) 以旧换新活动只针对使用一个周期后的旧产品,且参与以旧换新后的旧产品残值为0,消费者也无法通过第三方市场贩卖旧产品获得收益;(3) 前述研究表明,当新产品价格为内生变量时,新产品价格最优值恒为常数[10],因此此处为了简化分析将新产品价格设为外生变量,文中所涉及变量如表1所示.

表1 模型变量描述
两周期决策时序如下:第一周期伊始市场上并无持有A企业或是B企业产品的消费者,消费者在此时决定购买A企业产品或是B企业产品亦或是不购买,相应的消费者效用为θva-pa、θvb-pb、0;第二周期拥有旧产品的消费者决定参与以旧换新亦或是继续使用旧产品,参与以旧换新获得的效用为θva-pat、θvb-pbt,继续使用旧产品获得的效用为βθva、βθvb.据此,市场即被细分为购买A企业产品并参与以旧换新的消费者市场;购买A企业产品不参与以旧换新的消费者市场;购买B企业产品并参与以旧换新的消费者市场;购买B企业产品不参与以旧换新的消费者市场;不购买产品消费者市场.通过消费者市场效用划分,得5种类型的消费者效用如式(1)所示.
(1)
令V1=V2、V2=V3、V3=V4、V4=V5,得各市场划分点如式(2)所示[5].
(2)
3 模型求解
企业A与企业B的总利润由第一阶段的新产品销售利润(含参与以旧换新的消费者与不参与以旧换新的消费者第一阶段的购买行为产生的利润)和第二阶段的以旧换新产品销售利润组成.
(1-θ1)+(pa-ca)(θ1-θ2)
(3)
pb(θ3-θ4)
(4)
两企业就自身利润最大化进行博弈,求解获得如下命题.
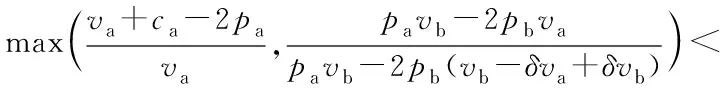

(5)
(6)
市场划分边界为:
(7)


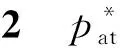
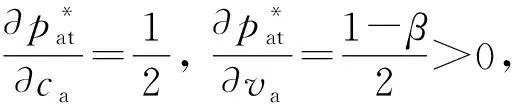

当不满足命题1的参数条件时,以旧换新价格约束与边界约束就不成立,某些市场的销量可能为0,同时也可能出现企业利润最优解不存在的情况,故不在本文讨论范围之内.
通过均衡解可得总销量、参与以旧换新市场与不参与以旧换新市场部分的销量以及总利润、参与以旧换新市场与不参与以旧换新市场部分的利润如下式所示.
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)

(19)



4 数值分析
为了探究划分边界θ以及相对应的销量随β变化规律,设定如下的数值算例参数:va=9,vb=4,ca=0.9,pa=5,pb=1,δ=1,结果如图1所示.


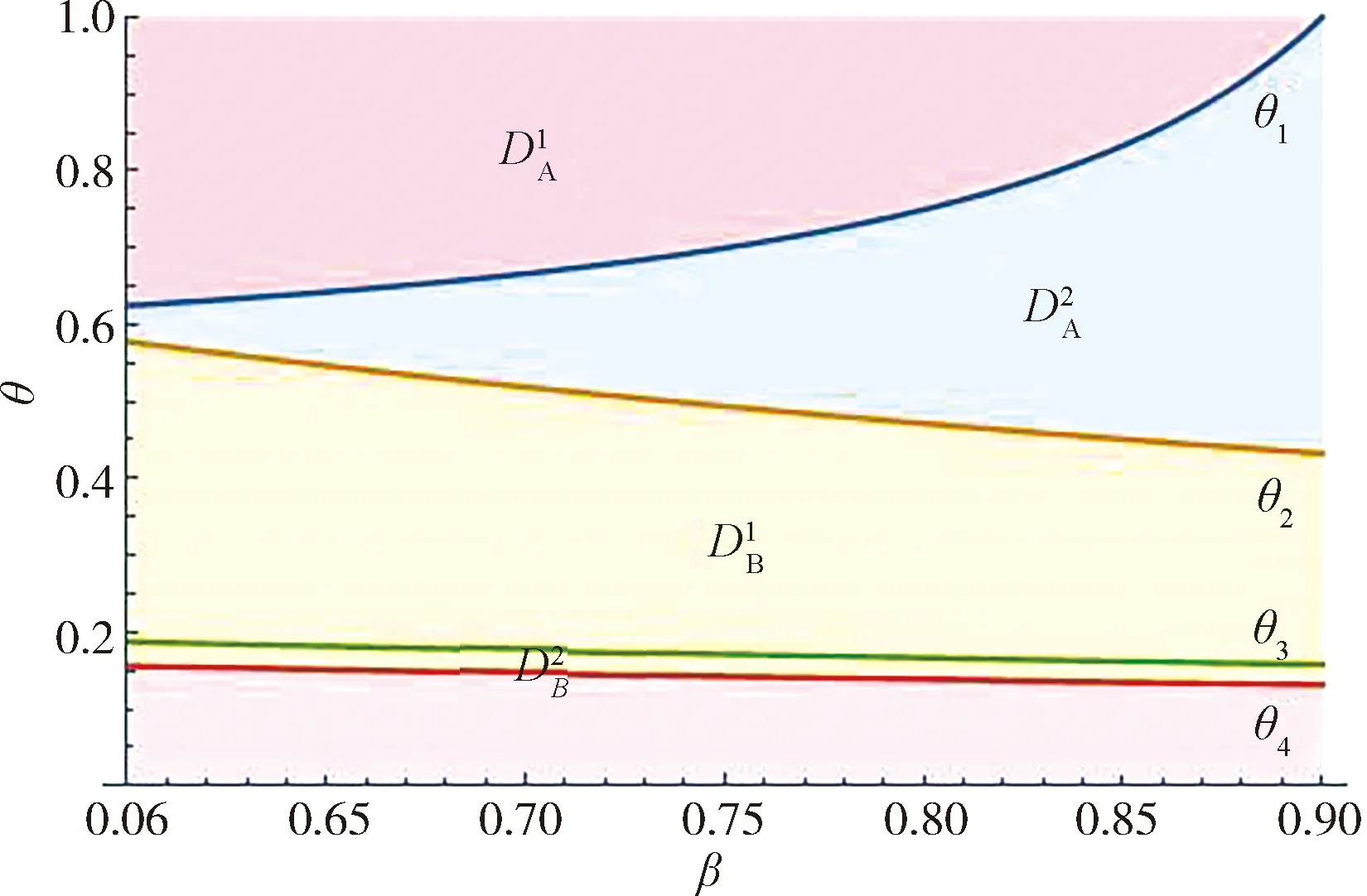
图1 划分边界随折旧系数变化图
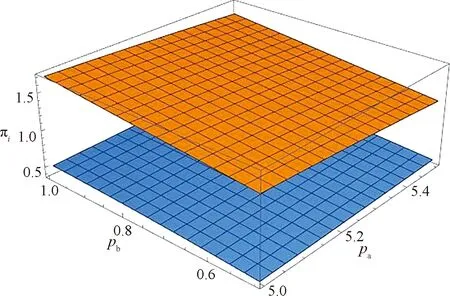
为了探究两企业利润随产品质量的变化,设ca=0.9,pa=5或pa=6,pb=1,β=0.8,δ=1,取9 从该数值算例能够发现,当B企业新产品质量上升,A企业产品质量下降;A企业利润下降,B企业利润上升,当数值超过一定阈值,B企业利润将会超过A企业利润;同时当A企业新产品价格更高时,B企业利润超过A企业利润的区间会增大. 设ca=0.9,va=9或va=8,vb=4,β=0.8,δ=1,取5 从该数值算例能够发现,当A企业新产品价格上升,B企业新产品价格下降,A企业利润下降,B企业利润上升.与前述算例不同的是,A企业利润恒大于B企业,但当A企业新产品质量更低,下降趋势会更快. 结合图2和图3数值算例分析,在以旧换新存在的两周期双寡头竞争市场内,企业间的产品质量差异以及价格差异的大小会影响企业的市场利润分配.相比于新产品价格,消费者更加注重产品质量水准是否符合相应的市场定位.在以旧换新存在的情况下,企业能更好笼络存量消费者,因此,新产品参数使得市场划分在第一周期伊始便产生了影响,企业管理者应当注意这样的现象. 本文通过设定两周期双寡头以旧换新博弈模型,获得了该模型的均衡解及相应的市场划分,并获得均衡状态下的企业销量与利润.通过对均衡结果的研究表明,只有当两企业产品质量差异较大,同时折旧系数适中的情况下,以旧换新定价均衡才存在.同时高质量产品企业作为市场引领者,可更自主地决定自身的以旧换新定价,并且由于其自身的高质量,在该均衡模型竞争中,不参与以旧换新的市场竞争能力更强.在两周期背景下,市场在第一周期便被划分,而以旧换新对企业的影响程度更多地体现在该企业消费者的范围内.因此,企业管理者应注意:(1) 精准定位自身产品质量档次,并制定相应的应对策略;(2) 合理利用以旧换新策略,低端企业尽量运用以旧换新策略维持消费者市场,耐用品市场的高端企业可以考虑适时放弃以旧换新市场.考虑回收其他企业的产品,同时考虑旧产品的第三方市场销售渠道,将会是本研究未来的方向.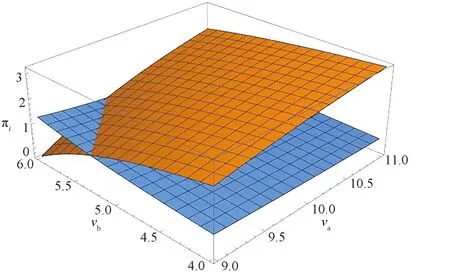
5 结 论
