一类非齐次Choquard方程的解整体存在与爆破的条件
2022-06-17何巧玲
何巧玲, 黄 娟
(四川师范大学数学科学学院 可视化计算与虚拟现实四川省重点实验室, 成都 610068)
1 引 言
本文研究如下非齐次非线性Choquard方程解整体存在及爆破的条件:
(1)
其中u(t,x):I×RdC是复值波函数,d≥3,b≤0,Iα是Riesz位势,即

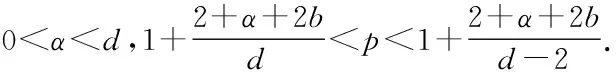

值得注意的是,在已有文献中,关于方程(1)的整体解和爆破解的相关结论都只考虑初值质能低于基态质能的情形. 一个自然的问题是:若初值质能高于基态质能,会有怎样的结果呢?对于这个问题,目前我们尚未发现有相关研究. 鉴于此,本文主要研究方程(1)当初值质能高于基态质能时解的整体存在和爆破的条件. 此外,受Lushnikov在文献[16]中所用方法的启发,我们利用Cauchy-Schwartz不等式和不确定原理,借助一个粒子在具有势垒场中运动的力学分析得到了方程(1)的一个新的爆破解存在的充分条件.
后文安排如下. 在第2节中,我们主要介绍方程(1)的局部适定性,Gagliardo-Nirenberg不等式及Pohozaev恒等式等预备知识. 在第3节中,我们给出并证明当初值质能高于基态质能时方程(1)解的整体存在和爆破的条件. 在第4节中,我们借助一个粒子在具有势垒场中运动的力学分析得到方程(1)的一个新的爆破解存在的充分条件. 在第5节中,我们对本文的主要结果作出总结.
2 预备知识

|·|b|u(t)|p)|u(t)|p)dx≡E[u0].
引理2.2(最佳Gagliardo-Nirenberg不等式)[15,17,18]对于任意的f∈H1(Rd),存在CQ>0,使得
(2)
其中
B=Np-d-α-2b=2(p-1)sc+2,

-ΔQ+Q-
(Iα*|·|b|Q|p)|x|b|Q|p-2Q=0
(3)
注1把(3)式两边分别乘以Q和x·∇Q后在Rd上积分,可得到Pohozaev等式
于是


(4)
|x|b|u|pdx=
(5)
引理2.4[19]设g∈H1(Rd),xg∈L2. 则有

证明 注意到

在(2)式中令f=eiλ|x|2g,则对任意λ∈R有
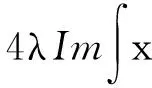
将上式视为关于λ的一元二次多项式,则不等式成立当且仅当关于λ的多项式的判别式为非正,即引理2.4. 证毕.
3 解整体存在及爆破的条件
定理3.1设u(t,x)是问题(1)的解,V(0)<∞,u0∈H1(Rd).令
M[u]1-scE[u]sc≥M[Q]1-scE[Q]sc
(6)
(7)
则
(i) 若有
M[u0]1-sc·
(8)
及
Vt(0)≤0
(9)
则u(t,x)在有限时间内爆破;
(ii) 若有
M[u0]1-sc·
(10)
及
Vt(0)≥0
(11)
则有
(12)
那么u(t,x)全局存在.
证明 由(5)式得
(13)
(14)
再由(4)式和引理2.4可得
(15)

(Zt(t))2≤4φ(Vtt)
(16)
令
由(13)式可知σ∈(-∞,8E[u]],从而
当φ′(σm)=0时,其中的σm满足
(17)

所以(6)式和(7)式分别等价于
σm≥0
(18)
及
(19)
(i) (9)式可写为
Zt(0)≤0
(20)
由(8)式和Pohozaev恒等式可得
结合(20)式得
Vtt(0)<σm
(21)
下证对任意t∈[0,T)都有
Ztt(t)<0
(22)
由(19)式和(21)式有
(23)
当证(22)式成立,我们反设(22)式不成立.则由(23)式知存在t0∈(0,T)使得Ztt(t0)=0且Ztt(t0)<0对任意t∈[0,t0)成立. 再由(19)式和(20)式,对任意t∈(0,t0]有
(24)
因此Zt(t)2>4φ(σm)成立. 由(16)式可知,φ(Vtt(t))>φ(σm)(其中t∈(0,t0]). 由(21)式及Vtt(t)的连续性,有
Vtt(t)<σm,∀t∈(0,t0]
(25)
根据式(23)(24)(25)可得
这与假设Ztt(t0)=0产生矛盾. (22)式成立.
(ii) 假设(6)式,(7)式,(10)式和(11)式成立.则(ii)等价于(18)式,(19)式及下列不等式成立
Zt(0)≥0
(26)
Vtt(0)>σm
(27)
注意到存在t0≥0,使得
(28)
取一个足够小的参数ε>0,满足
(29)
反设(29)式不成立.令
由Zt(t)的连续性有
(30)
及
(31)
由(16)式知
∀t∈[t0,t1]
(32)
因而φ(Vtt(t))>φ(σm)对任意t∈[t0,t1]成立. 这意味着Vtt(t)≠σm. 结合Vtt(0)>σm及Vtt(t)的连续性,可得到Vtt(t)>σm.
假设存在一个常数D>0,使得
(33)
将φ在σ=σm的泰勒展开式,则存在常数a>0使得
|σ-σm|≤1⟹φ(σ)≤φ(σm)+a(σ-σm)2
(34)
如果Vtt(t)>σm+1,则(33)式成立(对于足够大的D). 如果σm 4φ(σm)+4a(σ-σm)2. 因此有 从而得到(33)式,其中 但是,由(33)式和(30)式又可得 显然,对任意t∈[t0,T),(33)式都成立. 结合(13)式和Pohozaev恒等式,我们有 在本节中,不同于Zakharov[20]与Glassey[14]提出的经典爆破准则,以及陈波涛[21]提出的利用函数的可积性证明爆破解存在的方法,我们借助一个粒子在具有势垒场中运动的力学分析,结合Cauchy-Schwarz不等式和不确定原理获得问题(1)在有限时间内爆破的一个充分条件.这是对Lushnikov方法[16]的一个推广. (35) 其中-1<δ<γ,0<γ<1,0<ω<1.定义泛函 若v是问题(35)的一个非负解,使得以下任意一个条件成立: (i)ε(0) (ii)ε(0)>Umax,vs(0)<0; (iii)ε(0)=Umax,vs(0)<0;v(0)<1, 那么v在某个有限时间T+内达到零点. 定理4.2设u0∈H1(Rd),V(0)<∞,E[u]>0.若 其中N=[d(p-1)-(2+2b+α)],k=sc(p-1), 且 则方程(1)的解在有限时间内爆破. 证明 由于 则 由Cauchy-Schwarz不等式,有 即 将上述不等式代入(5)式,可得 Vtt(t)≤8[sc(p-1)+1]E[u]- (36) 令 其中 对任意t∈[0,T+),(36)式可以改写为 (37) 这里,若N=[d(p-1)-(2+2b+α)]则令B(t)=Bmaxv(s),s=at.从而有 (38) 从而由(37)式可得 (39) 借助一个粒子在具有势垒场中的力学运动分析(39)式,则可将其改写成 (40) 其中 为粒子的电势, 设v=v(s)(质量为1)是在以下两种外力作用下运动的粒子坐标: 其中g2(t)是将粒子拉向零点的未知非负外力. 如果粒子在有限时间内到达零点,则意味着会发生坍塌;如果粒子到达零点时没有受到外力-g2(t),那么当它受到这个力时一定会更快地到达零点. 所以,我们考虑方程 (41) 并定义粒子v的能量为 (42) 由(41)式知能量是守恒的. 如果粒子在有限时间内到达零点,即存在t<∞使得v(t)=0,则有V(t)=0,方程(1)存在爆破解. 由引理4.1,满足(41)式的爆破条件为 (i)ε(0) (ii)ε(0)>Umax,vs(0)<0; (iii)ε(0)=Umax,vs(0)<0;v(0)<1, 那么v会在某个有限时间T+内达到零点. 则有 (43) 令k=2β=sc(p-1). 则有函数 (44) 于是爆破条件(i)~(iii)可以写为 因此,我们有 其中 定理得证.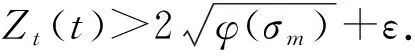
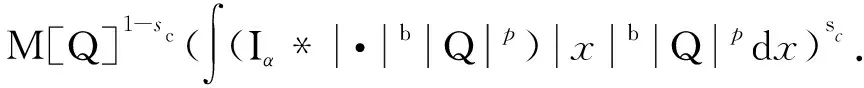
4 解爆破的新条件







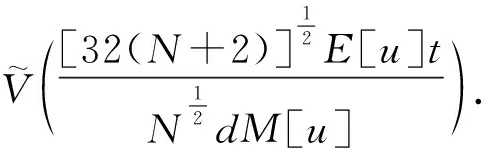
5 结 论

