相场晶体方程的一个高精度能量稳定数值格式

李贵川 , 赖 倩 , 胡劲松 , 冯端宇

(1.西华大学土木建筑与环境学院, 成都 610039；2. 西华大学理学院 成都, 610039； 3. 四川大学数学学院, 成都 610064)

1 引 言

作为一种在空间原子尺度上模拟晶体的新方法, 相场晶体模型[1]能够通过极小化Swift-Hohenberg (SH) 型自由能量泛函来解释晶格的周期性结构及弹性和晶格的塑性变形、位错、晶界等各种微结构现象.此类模型主要采用相变量来描述原子密度的时间平均值,并与动态密度泛函理论密切相关[2]. 相场晶体模型具有能量泛函

(1)

其中Ω=[0,L]×[0,L]∈R2,φ:Ω→R表示密度场,a=1-ε为常数,ε是与相场温度有关的常数. 相场晶体方程是由能量泛函(1)导出的H-1梯度流,即

φt=Δ(φ3+aφ+2Δφ+Δ2φ)

(2)

本文假设φ和Δφ在Ω上都满足周期边界条件.因此，方程(2)是质量守恒的，同时其能量泛函(1)随时间变化保持单调不增.

相场晶体方程(2)是一个六阶非线性偏微分方程，难以获得解析解，因而寻找高效数值算法尤为重要.构造相场晶体方程数值算法的主要困难在于非线性项和高阶导数项对时间步长存在苛刻的稳定性限制.此外，由于需要在较长时间模拟过程中尽可能保证结果的准确性，数值格式的能量稳定性也是一个关键因素.Backofen等[2]提出的有限元方法本质上是标准后向欧拉格式，其中的非线性项φ3通过 (φk+1)3≈3(φk)2φk+1-2(φk)3逼近，因而无法保证能量稳定性和可解性；Cheng和Warren[3]提出的线性化谱格式则不能在理论上证明该格式无条件能量稳定；Yang等[4]给出的线性化一阶及二阶数值格式具有能量稳定性，但φ的H2-稳定性无法得到证明.此外，Hu及Wise等[5,6]利用凸分解方法讨论了相场晶体模型的无条件稳定的差分格式, 给出了时间方向一阶及二阶、空间方向二阶精度的无条件收敛证明；李娟[7]提出了具有时间二阶精度和空间四阶精度的线性化三层差分格式，研究了格式的收敛性但没有给出能量稳定性分析. 另一方面，在时间高精度数值方法上,目前仅有的工作是Shin等[8]利用凸分解的思想构造的时间上精度能达到三阶的凸分裂龙格-库塔格式，格式具有能量稳定性和唯一可解性.更多的数值算法可参看文献[9-12].

本文针对相场晶体方程在时间上采用三阶后向差分公式、空间上利用理论上具有谱精度的Fourier拟谱逼近构造了一个高精度数值格式.为保证数值格式的能量稳定性，我们在格式中增加与时间阶精度匹配的Douglas-Dupont正则项，进而在理论上证明了格式对于修正离散能量泛函的稳定性.最后本文给出了数值算例，以验证格式精度以及长时间数值模拟的有效性.

2 Fourier拟谱逼近及数值格式

为表述方便，本文选择单位正方形区域，即L=1. 假设hx=hy=h,Nx=Ny=N,N=2K+1始终是奇数. 网格点记为 (xi,yj),xi=ih,yj=jh, 0≤i,j≤N. 对于二维数值网格上的周期函数f, 定义网格函数空间

如果f,g∈GN，相应的有限项离散Fourier展开式为

(3)

并且有∇N·∇Nf=ΔNf. 对网格函数f，引入离散算子(-ΔN)γ,γ>0，

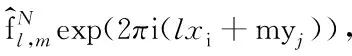
对于定义的这些算子，通过离散的分部积分公式可以确保如下列等式恒成立：

〈f,ΔNg〉=-〈∇Nf,∇Ng〉，

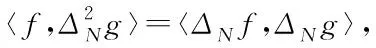
(4)

〈f,g〉-1,N=〈f,(-ΔN)-1g〉=

〈(-ΔN)-1/2f,(-ΔN)-1/2g〉.

所以‖·‖-1,N可以定义为

至此，我们得到相场晶体方程能量的离散形式：

对于任何的周期网格函数φ∈GN，离散能量为

(5)

对于相场晶体方程(2)，时间离散采用三阶向后差分离散，空间上采用Fouier拟谱逼近，同时为保证格式的能量稳定性，增加Douglas-Dupont正则项，从而得到如下具有精度O(Δt3+hm)的数值格式:

(6)

此处

μn+1=(φn+1)3+aφn+1+2ΔN(3φn-3φn-1+

(7)

m表示空间谱精度的阶数，具体取值依赖于空间网格点的划分.

注1格式(6)是一个三步数值格式，初始层数据φ-1，φ-2必须给定. 如果选择φ-1=φ-2=φ0, 能量估计会变得更简单, 但是在初始阶段，时间层的三阶精度会退化. 另一方面, 也可以选择三阶的龙格-库塔格式计算φ1,φ2，这样就能够保证初始时间层上达到理论上的三阶收敛精度.

3 格式的可解性及能量稳定性

证明 对于(6)式中的ΔNμn+1，根据周期边界条件，可以得到

(8)

定理3.2如果φn,φn-1,φn-2∈GN，则数值格式(6)(7)存在唯一解φn+1.

证明 令

(9)

此处

(10)

非线性方程(9)的解能够看作下述离散能量泛函的极小值：

根据凸优化理论，该泛函是严格凸的，因此该泛函的极小值存在且唯一，也就表明格式(6)(7)的数值解也是存在唯一的. 证毕.

(11)

此处

(12)

证明 将式(6)与(-ΔN)-1(φn+1-φn)作内积，得

〈ΔN(φn+1)3,(-ΔN)-1(φn+1-φn)〉-

a〈ΔNφn+1,(-ΔN)-1(φn+1-φn)〉-

2〈Δ2N(3φn-3φn-1+φn-2),(-ΔN)-1(φn+1-φn)〉-

AΔt2〈Δ2N(φn+1-φn),

(-ΔN)-1(φn+1-φn)〉=0

(13)

对上式中的第一项，可以推出

(14)

由离散的分部积分公式及式(4), 对于非线性项有

(15)

及

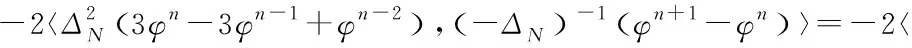
∇N(φn+1-φn)〉=2〈∇N(-φn+1+φn+1-2φn+φn-1-(φn-2φn-1+φn-2)),∇N(φn+1-φn)〉≥

(16)

而且，如下三个等式也是显然成立的:

(17)

(18)

(19)

将式(14)～(19)代入式(13), 可得

(20)

注意到

(21)

注2形式上定理3.3的结果表明本文只能够证明数值格式(6)(7)对于修正的离散能量(12)而不是原始离散能量(5)的稳定性. 实际上，如果假设φ-1=φ-2=φ0，则离散能量(12)的稳定性能够保证离散能量(5)的稳定性. 这是因为

即任何时刻的能量都不会超过初始时刻的能量值.

4 数值算例

4.1 精度验证

本节首先验证数值格式(6)-(7)在时间方向上的三阶精度.计算区域Ω=[0,1]×[0,1]，并假设相变量的精确解为:

(22)

为了与方程(2)保持一致，在方程(2)的右端需要增加一个外力项f(x,y,t)，即

f(x,y,t)=(φe)t-Δ(φe3+aφe+2Δφe+Δ2φe)

(23)

对于时间方向的误差验证，为了避免空间谱精度带来的影响，取空间方向网格划分数N=256，使得空间方向的误差可以忽略不计. 在计算过程中，选择两个参数A和a的不同组合，计算结束时间为T=1，时间步长从0.1开始依次减半计算，相变量φe相应的‖·‖2误差及收敛阶数的计算结果见表1.

表1 不同参数组合下的时间方向的‖·‖2误差及阶数

从表1结果可以看出，正如在注3中所说，尽管理论上对系数A的要求极高，但在数值模拟时却没有这一限制条件， 无论是A=1还是A=10. 不过需要提及的是, 从表1中的误差结果看出，虽然A的值选择越大越能够在理论上保证能量稳定性，但越大的A也会导致更大的数值耗散, 从而导致绝对误差变大.

对于空间方向的误差估计，选择A=1,a=0.975以及时间步长Δt=10-4. 随着空间网格逐渐加密，计算相变量在T=1时的误差，计算结果见表2. 从结果可以看出，谱精度随着空间网格划分数N的增加快速提升，但无法得到类似时间方向的误差的具体阶数. 这主要由于谱精度的作用, 随着N的增大, 数值解的绝对误差已经变化不大，因为这个时候的误差已经不是空间离散主要引起的，而是时间方向误差的体现.

表2 空间方向的‖·‖2误差

4.2 相场晶体的动力学模拟

考虑二维空间区域Ω=[0,128]×[0,128], 数值格式(6)(7)中的参数选取为A=1,a=0.975，空间步长固定为h=1，晶体相的初始状态值为

φi,j=0.06+0.03ri,j

(24)

其中ri,j为[0,1]服从均匀分布的随机数. 为提高计算效率，采取不同的时间步长进行数值模拟，即在时间区间[0,100]上取Δt=0.01，在[100,2000]上取Δt=0.1，相场晶体的动态演化在不同时间的状态见图1.

(a)

(b)

(c)

(d)

图2也给出不同时刻下的离散能量泛函(5)的计算结果. 显然，离散能量的演化和理论分析结果一致，即保持单调不增. 开始时由于时间步长较小，使得图2中能量变化比后一段较大时间步长时能量变化平缓；中间段能量变化较剧烈，但随着能量衰减到一定程度，能量变化呈现出平缓状，此时晶体相或者密度分布基本处于平稳状态.

接下来取晶体相的另外一种初始状态下晶体微结构的变化. 先取晶体相的初始状态值为φi,j=0.02ri,j，然后再四个空间点处增加四个点状相场值(见图3a)，其值分别为10、5、8和10. 随着时间增加，晶体相场的演化见图3. 可以看出，在初期阶段时四个点源项在演化过程中互不干扰，但较长时候后，各点的演化互相影响，同时由于相场值的差异，导致不对称的微结构出现.

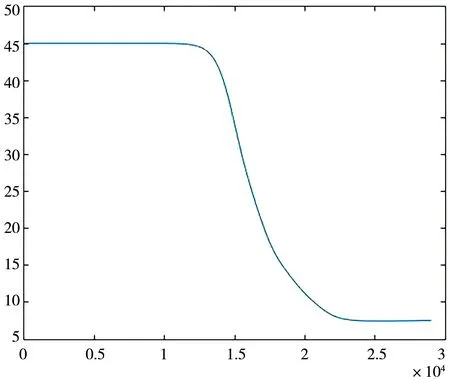
图2 晶体能量的动态演化图Fig.2 The evolution of the discrete energy

(a)

(b)

(c)

(d)

5 结 论

本文针对相场晶体方程的周期边界问题，提出了一种具有能量稳定性的Fourier拟谱数值格式. 由于能量稳定性是在材料微观结构的长时间数值模拟时本质物理属性的要求, 因此我们在时间采用后向差分的三阶高精度离散, 并增加Duglas-Dupont正则项以确保能量稳定，并以理论上证明了数值格式的质量守恒性、数值解的存在唯一性以及格式的能量稳定性. 数值模拟结果既验证了本格式在时间和空间上高精度离散逼近, 同时也展现了相场晶体方程所描述的材料结构的微观变化以及能量的演化趋势.