一类具有logistic源的高维Keller-Segel模型的爆破

刘梦琦， 李嘉文， 韩永杰

(西华大学理学院， 成都 610039)

其中χ>0，λ≥0，μ≥0，k>1，证得当n≥5时若则问题解在有限时间爆破. 这表明在高维情况下即便有 logistic源的存在也不能排除爆破的发生.

1 引 言

趋化是环境中化学物质影响物种运动的一种生物现象，可以驱动细菌的定向运动或部分定向运动，也是细胞迁移的重要手段之一[1-3].1970年，Keller和Segel[4,5]根据这种运动提出了如下模型:

(1)

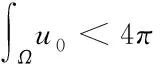
考虑到很多情况下化学物质的扩散速度要比细胞扩散速度快得多，方程组(1)可简化为如下抛物-椭圆模型:

(2)

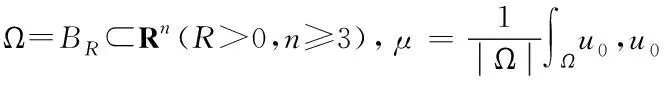
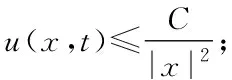
(ii)如果

|∇v(xj,tj)|→∞，其中(xj,tj)→

(x0,T),j≥0}，

r∈(0,R)

(3)

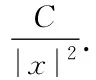
令Ω=Rn，μ=0，u0为径向对称的非负函数.关于方程组(2)的柯西问题有，如下结果[12,13]:

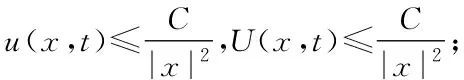
由细胞动力学理论，在大时间情况下细胞的增殖与死亡也应该被考虑.因此我们有如下的具有logistic增长项的模型:

其中f(u)=λu-μuk，λ≥0，μ≥0，χ>0，k>1， Ω⊂Rn(n≥1)是具有光滑边界的有界区域.关于方程组(4)的齐次Neumann初边值问题的主要结果如下:

(i) 如果n=2，k≥1，初始时刻质量大于8π，则方程组的解在有限时间爆破[14];

如果将第二个方程变为vt=Δv-uv，k=2，则方程组存在整体有界经典解[18].

本文研究如下模型:

(5)

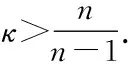
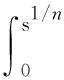
t∈[0,Tmax)，

这里w(s,t)相当于一种质量的转换.这种方法基于ODI分析[20]，该方法已经被证明可以用于有限时间爆破的证明[16,17]. 为了后面方便计算，记

(6)

本文主要结果如下：

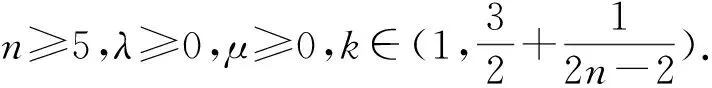
2 预备知识

2.1 解的局部存在性、正性

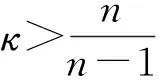
(7)

引理2.2方程组(5)的解(u,v)对所有t∈(0,Tmax)满足u(x,t)>0，v(x,t)>0.

证明 令截断函数ξ∈C∞(R)，

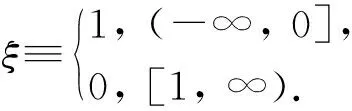
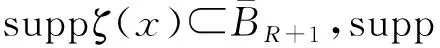
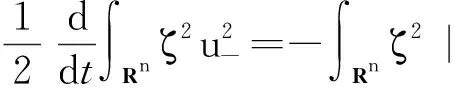
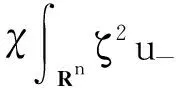
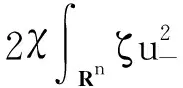
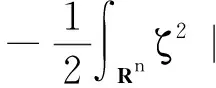
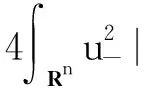
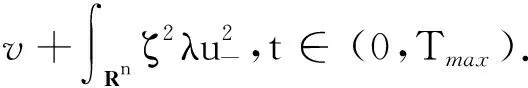
因∇v∈L∞((0,Tmax);Lq(Rn))，由Gagliardo-Nirenberg不等式和Hölder不等式可知，存在C1>0和C2>0使得

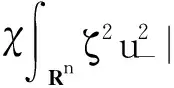
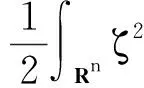
由截断函数的定义可知，存在C3>0和C4>0满足

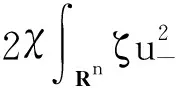
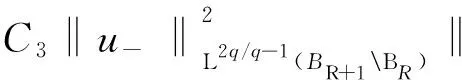
定义

则yR(t)满足

对于p∈(1,∞),有

根据引理2.1，当R→∞时有

因此，对任意的t∈(0,Tmax)，当R→∞时有yR(t)→0. 再根据强极值原理可知u为正. 又因为

所以可以直接得到v>0.证毕.

引理2.3假设λ≥0，μ≥0，对任意t∈(0,Tmax)，则m(t)≤m0eλt.

证明 由Hölder不等式和Hardy-Littlewood-Sobolev不等式可知，存在常数A>0满足

‖u(·,t)∇v(·,t)‖L1(Rn)≤

‖u(·,t)‖L2n/n+1(Rn)·‖∇v(·,t)‖L2n/n-1(Rn)≤

根据引理2.1，当R→∞时有

引用引理2.2中的截断函数ζ(x)，由方程组(5)中第一个方程可知

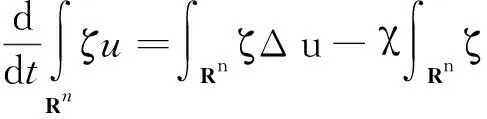
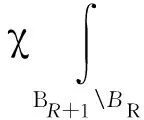
所以存在常数c1,c2>0满足

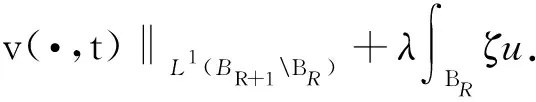
由常数变易法可知

c2‖u(·,t)∇v(·,t)‖L1(BR+1BR))ds.

再由引理2.1可知u∈C0([0,Tmax);L1(Rn)∩Lκ(Rn)).令R→∞，得

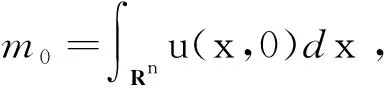
2.2 方程组到单个抛物方程的转换

设u0∈C1(Rn)是径向对称的.由引理2.1知解(u,v)是径向解. 令u=u(r,t)，v=v(r,t)，r=|x|∈[0,∞). 对任意t∈(0,Tmax)，有

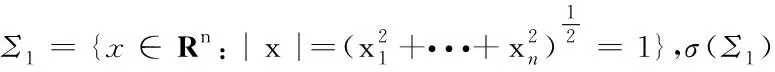
受文献[19]的启发，引入

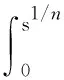
t∈[0,Tmax)

(8)

则

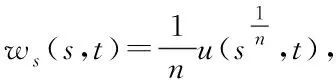
因u非负, 所以ws(s,t)>0在(0,∞)×[0,∞)上，且存在η>1，t∈[0,Tmax)，s∈[0,∞)使得

w(s,t)≤m(t)η

(9)

根据方程组(5)第二个方程有

结合方程组(5)第一个方程可得

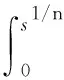
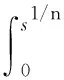
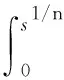
其中f(u)=λu-μuk.从而w满足如下单个抛物方程：

s∈(0,∞),t∈[0,Tmax).

所以，

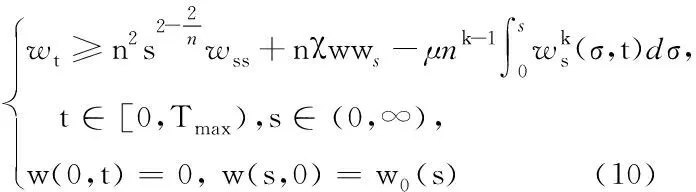
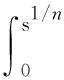
(11)

3 解的懪破

引理3.1假设λ≥0，μ≥0，n>2，u0(x)是径向的，(u,v)为模型(5)在Rn×(0,Tmax)上的解.则对任意α>1，p∈(0,1)，t∈(0,Tmax)有

(12)

其中w0为(11)式中所定义.

证明 将(10)式的第一个不等式两边同乘以e-s(s+ε)-αwp-1(ε>0)，然后在(0,∞)上积分可得

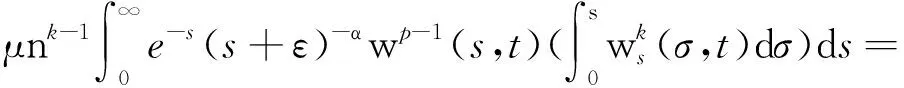
I1+I2+I3,s∈(0,∞).

对I1分部积分，有

根据引理2.2可知u>0.所以

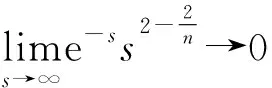
又因为

所以

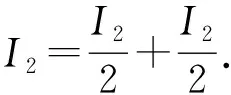
由分部积分可知

根据上述分析得到

对t∈(0,Tmax)成立. 由单调收敛定理，当ε→0时(12)式成立.

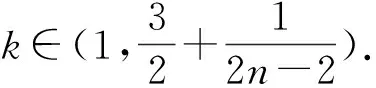
其中w∈C1(0,∞),

证明 根据Fubini定理有

因α>1，p∈(0,1)，故

对任意ε>0，应用Young不等式可知C1>0满足

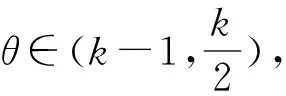
综上，结合引理3.1我们可以找到合适的α>1，p∈(0,1)，使得所需积分不等式成立.证毕.

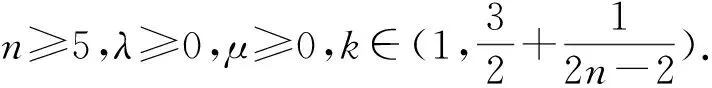
CeΛtt， ∈(0,Tmax)，

其中的w0(s)由(11)式给出.

p∈[0,1]，α≥1

(13)

满足

根据连续性可知，存在α0>1，p0∈(0,1)，使得对任意p∈[p0,1)，α∈(1,α0]有

g(p,α)≥0

(14)

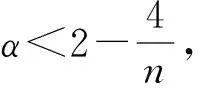
(15)

由引理3.1可知

J1+J2+J3+J4-J5-J6，

其中

由Young不等式，存在C2>0满足

及C3>0满足

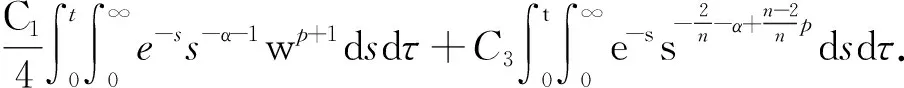
所以有

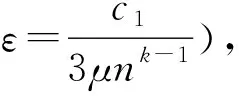
这里的g(p,α)为(13)式所定义.由(14)式可知g(p,α)≥0.由(9)式和引理2.3可知

w(s,τ)≤ηm(τ)≤ηm0eλτ，s∈(0,∞)，

τ∈(0,Tmax).

从而可以找到常数C6>0满足

t∈(0,Tmax).

综上，取Λ=λg(p,α)，则存在C>0满足

其中

因1-α+p>0，所以有

t∈(0,Tmax).

引理得证.

为了更好地运用引理3.3中的积分不等式, 我们首先陈述下面的Gronwall引理：

引理3.4[10]令α>0，δ>0，β>0. 若对某个T>0，使得非负函数y∈C0[0,T]对所有的t∈(0,T)满足

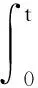
(16)

由引理3.3, 对任意的t∈(0,Tmax)有

且

所以有

令

则φε(s)是非负函数，且当ε→0时φε(s)→m0η对所有的s∈[0,1]成立. 因

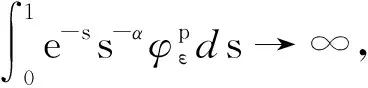
综上，有

令