应用于非精确图匹配的改进DF 模型

李智杰，伊志林，李昌华，张 颉

西安建筑科技大学 信息与控制工程学院，西安 710055

图（graph）在众多的科学领域及工程领域（如计算机、医学、生物、化学、建筑等）具有广泛的应用。作为数据的一种表示形式，能够描述现实世界中复杂的结构数据，如化合物集合、蛋白质结构、社交网络等，图强大而复杂的信息表达能力吸引了诸多学者的深入探索。

图匹配主要分为精确图匹配与非精确图匹配，其算法层出不穷。图匹配问题已被证明是一个非确定性多项式（nondeterministic polynomially，NP）问题，相对比之下非精确图匹配允许算法在一定范围内的容错匹配机制得到了学者的广泛关注，如图嵌入方法、基于约束松弛的方法、图核等诸多的非精确图匹配的方法被研究学者应用到图上，不同程度上为非精确图匹配算法在领域内发展作出重要贡献。目前传统算法在准确率以及有效性等方面难以满足越来越多领域的应用需求。

深度森林（deep forest，DF）是当前深度学习下的新框架，能够对不同领域中存在的问题提供高效而便捷的解决方案。深度森林相对于现有的神经网络具有对超参敏感性小，在数据集的规模上适应范围大，同等条件下模型收敛速度快且高效等优点。利用DeepForest 实现非精确图匹配算法旨在提高目标的分类识别率与精度，从而解决应用研究的需求不足问题。在深度学习研究领域中，文献[6]首次提出了DeepForest 学习模型，模型包含多粒度扫描和级联森林两部分，分别承担不同的责任角色。其中多粒度扫描的功能与文献[14]提出的基于移动块搜索的特征选择随机森林方法的思想不谋而合，在一定程度上提升了样本的多样性以及完整性，但是从图结构信息的整体关联性与对局部信息增强的角度上分析，不能较好地表达图结构信息。对于与非精确图匹配算法的结合，文献[15]针对级联森林深处的决策树的精确概率模型，以实际研究的需求为目标进行了相应的改良或变化，利用Dirichlet 模型的区间值概率替代精确的概率类分布，提出了非精确图匹配的分类模型。文献[16-18]针对决策树叶节点的不同影响因素致使模型精度下降的问题，提出了采用权重方式的不同解决方案。虽然实际问题描述不同，但是问题的目标均为提高模型分类的准确性，采取权值规则方式增强模型的分类效果，提高训练效率与准确性。

上述方法虽然在不同角度对模型进行了局部改良或优化，但在非精确图匹配应用上，由于图结构信息语义复杂的特点以及模型结构自身等因素导致识别率上的差异。为充分利用深度学习高效、快速的优势，本文在DeepForest 模型的基础上改良多粒度扫描算法，同时结合定义的权值策略规则，提出一种改进DF模型（improved DeepForest，IDF），并将其应用于非精确图匹配，达到提升图匹配识别率与精度的目的。文献[6]中的DeepForest在文中称为原生深度森林（DF）。

1 IDF 模型

IDF 模型整体框架主要分为复合多粒度扫描与加权级联森林两个模块。复合多粒度模块在多粒度模块的基础上结合随机采样的方式对模块的采样进行改进优化；加权级联森林则定义了集中决策时的权值规则，决策过程中不断降低影响因子小的决策枝对结果的贡献值。

1.1 复合多粒度扫描

复合多粒度扫描主要是对高维数据进行特征提取。针对图数据结构的复杂性与节点间的信息交互传递的特性，单一滑动窗口获取的样本在样本整体的拟合优势上存在欠缺。按照随机的原则，即保证总体中每一个对象都有已知的、非零的概率被选入作为研究的对象，保证样本的代表性，结合随机窗口采样可以弥补样本特征集的拟合优度与多样性。

设长度为的一维特征向量，使用长度为的窗口进行滑动扫描且每次滑动步距为1 个单位，产生(-+1)个具有维特征向量的数据子集F。每次窗口滑动同时随机捕获相同维度的特征向量数据子集F，进而将两者合并构成(-+1)个具有2维特征向量的数据子集G，如式（1）所示。

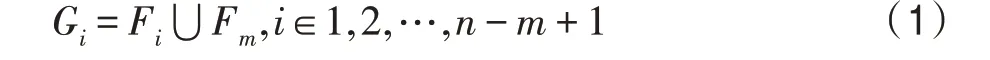
同理，对于一个×的二维数据采取相同的方式获取样本的特征向量数据子集，将两者复合构成新的维度特征向量的数据子集，并作为级联森林的输入。整个复合多粒度扫描算法和结构如算法1 和图1 所示。

复合多粒度扫描算法

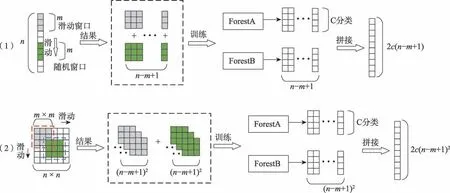
图1 复合多粒度扫描Fig.1 Compound multi-grained scanning

算法1 的时间复杂度虽然仍维持为()，但由于随机窗口采样的随机选择性，在移动扫描的同时对样本的局部或整体给予关注。对于作为级联模块的输入数据，相较单一滑动窗口的数据采样，并非所有特征的特征属性都对其分类研究有真同等重要的地位，复合采样构成的特征数据子集体现了样本的拟合优度，弥补了在特征分类上的不足。

1.2 加权级联森林

加权级联森林作为整个模型的另一核心模块，以复合多粒度扫描模块处理的数据特征子集为输入，以模型最终的分类结果为输出，对模块底层内的决策树采取权值策略规则，降低决策树因等权决策机制对结果产生的决策差异，提高模型的分类准确率。在本模块内单层森林的具体结构如图2 所示。

式中，为数据集的标签分类数，p表示数据被第棵树分为第类的概率。

图2 单层级联森林概率分布Fig.2 Probability distribution of single-level cascade forest

定义函数max()用于计算概率矩阵中列向量的最大概率分量值，即

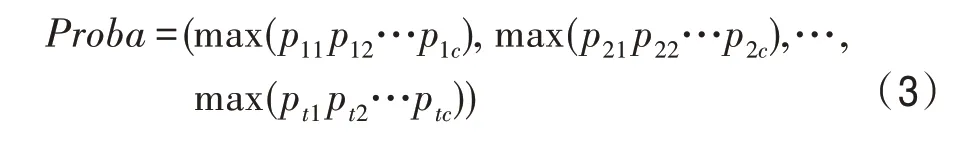
根据图2定义决策树的迭代权值规则，在式（3）中：

（1）当max()所对应分量值的列下标与数据集的真实映射分类标志相同时，取：

（2）其余情况则取：

其中，p为概率分布中列下标与数据集的真实映射分类相同的概率分量；表示当前层当前森林的第棵树。即：

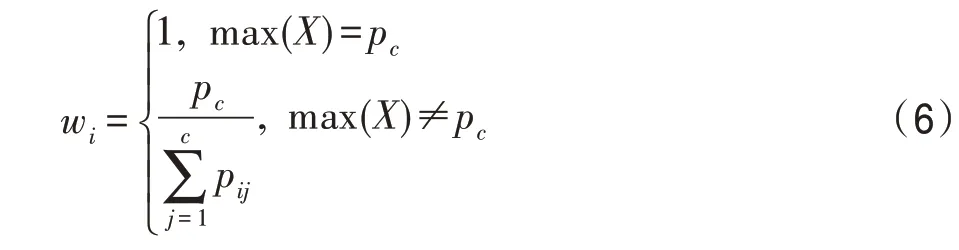
由式（6）得到单层森林的权重概率和为：

当结果不满足模型设定的阈值时，由式(6)计算出本层森林决策树的权重值，对比上一层的权重值，降低训练过程中精度不准确的决策树对决策结果的权重比例，取min(,)作为当前森林中决策树的权重赋值函数，继续深入扩展直至满足模型设定的阈值时停止，输出最终的分类结果。

加权级联森林算法

图2 以及算法2 结合图匹配算法以提升准确率为目标，虽然算法的时间复杂度维持为(×)，但采用权值策略规则对级联森林底层的决策树赋权优化，加速了模型在迭代过程中的收敛速度。通过加权方式降低了森林中各子树在迭代过程中被逐级放大的决策差异与模型结构的深度，提升了模型在图匹配算法应用上的性能。

IDF 算法

算法3 描述了IDF 算法在非精确图匹配上的训练与预测过程，其中步骤5 调用算法1 对实验数据进行复合多粒度扫描，而步骤7 调用算法2 对模型进行训练。算法3 虽然在时间复杂度上没有发生变化，但是算法整体上既兼顾图结构信息特点，又在图匹配算法上的分类准确率及扩展级上体现其优势。

2 实验与分析

在实验部分中，为方便比较模型的实验效果，采取控制单一变量原则构建了实验所涉及到的对比模型：复合多粒度深度森林（compound multi-grained deep forest，CMDF）模型和加权级联深度森林（weighted cascade deep forest，WCDF）模型。其模型的具体结构关系如图3 所示。

为验证模型在非精确图匹配上的实际效果，对多个不同的标准数据集进行了训练和测试。对比实验中所使用的具体模型结构详见图3，针对不同模型分别做了三组对比实验，测试时选取每个数据集中的80%数据用于训练，20%的数据则用于测试。

实验中的评价指标主要为实验数据的分类准确率，其中在IDF 算法的对比中增加了扩展级数的评价指标，绘制实验图表以及采用平均值的方式对不同算法的实验结果列表对比。

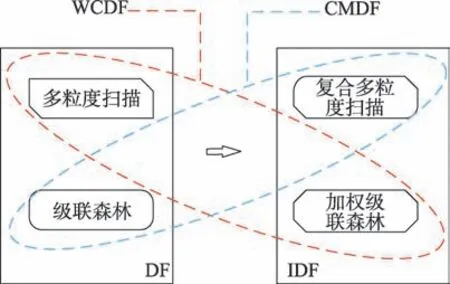
图3 模型结构关系Fig.3 Relationship of model structure

2.1 实验数据集

实验中采用的标准数据集信息如表1 所示。

表1 数据集信息Table 1 Information of dataset

2.2 实验结果与分析

为验证复合多粒度扫描算法，与文献[6]中的DF模型进行对比实验。实验参数采用文献[6]中的参数列表，模型评价以准确率为指标，图的横轴表示实验次数，纵轴表示实验的准确率，实验结果如图4 所示。

实验结果表明，复合多粒度深度森林的平均准确率为MUTAG-92.2%、PTC-72.1%、COX2-91.8%，略高于DF 的MUTAG-91.7%、PTC-71.3%、COX2-90.7%。究其原因，对于图结构数据，采用随机窗口融合移动扫描窗口的取样方式，在一定程度上既关注了图结构的整体信息，也对局部信息给予加强，增加了样本的拟合优度与多样性，提升了模型的分类性能。

为验证加权级联森林算法，与文献[6]中的DF 模型进行对比。图的横轴表示实验次数，纵轴表示实验的准确率，实验结果如图5 所示。

图5 中，在MUTAG、PTC、COX2 数据集的实验结果显示，加权级联深度森林的准确率曲线位于DF之上，平均准确率分别为93.1%vs91.7%(MUTAG)、72.5%vs71.3%(PTC)、91.8%vs90.7%(COX2)。究其原因，图的复杂结构特征在经过加权级联森林的决策树分类时，利用算法2 的权值策略规则在迭代过程中不断降低分类效果差的决策树对分类结果的贡献，以此达到提高模型分类准确率的目的。

图4 复合多粒度深度森林准确率Fig.4 Accuracy of compound multi-grained deep forest

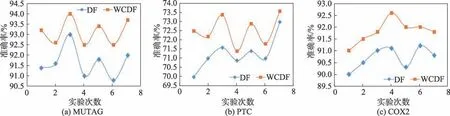
图5 加权级联深度森林准确率Fig.5 Accuracy of weighted cascade deep forest

图6 三个数据集上两种算法的准确率Fig.6 Accuracy of two algorithms on three datasets

为验证IDF 算法的整体分类效果，实验分别采用在数据集上的准确率与级联结构所生成的扩展级数作为评价指标。扩展层级的对比实验采用传统深度学习的栈式自动编码机（stacked autoencoder，SAE），图的横轴表示实验次数，纵轴表示实验的准确率，具体实验数据如图6 及表2 所示。

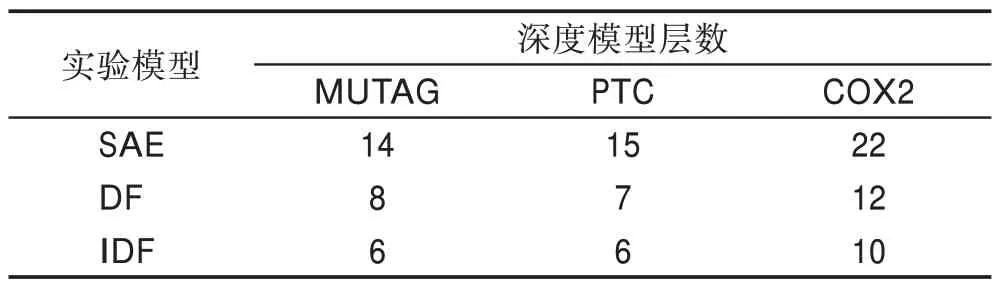
表2 深度模型层数Table 2 The number of layers in depth model

由图4～图6及文献[12]得到的在不同模型下针对相同数据集测试的平均准确率对比结果如表3 所示。

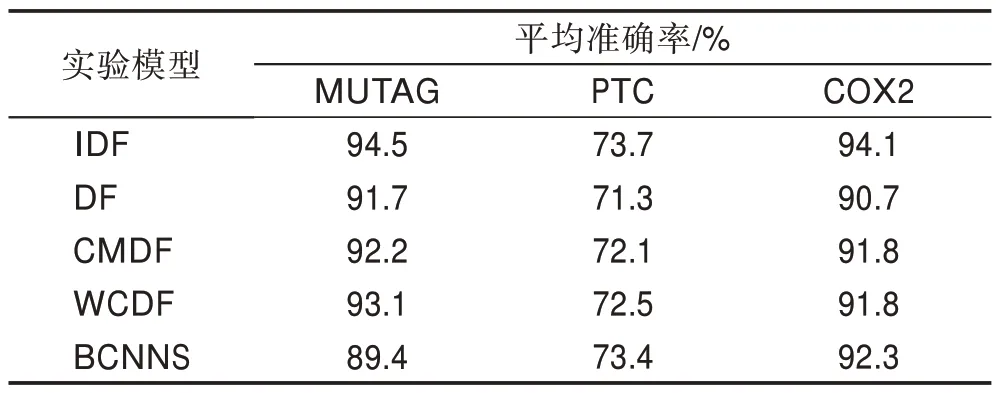
表3 数据集的平均准确率Table 3 Average accuracy of dataset

结合图6、表2、表3 可以得到在数据集MUTAG、PTC、COX2 上，IDF 模型取得的平均准确率分别为94.5%、73.7%、94.1%，相较于现有的DF 算法，部分优化的CMDF、WCDF 算法，以及结合神经网络的BCNNS 算法，实验结果有明显的提升。相较于传统的深度学习方法，深度森林减少了超参数的同时，对不同规模的数据适应性强，能够迅速收敛，提升算法的效率及准确性。对于改进的模型，IDF较DF算法在扩展层数的图上略显优势，降低了1至2个单位的扩展层数。

现有的DF算法相较于神经网络算法，避免了数据规模小的困窘，同样的参数下模型迅速得到极佳的性能。IDF算法在原先深度学习的优势下，继承了CMDF算法通过随机窗口对图结构数据在局部与全局的关注，以及WCDF算法利用权值加速模型收敛减小决策误差的优势，实现了IDF算法整体上的性能提升。

3 结束语

深度森林是一种基于树的集成学习方法，它通过对树构成的森林进行集成并串联以达到让分类器进行表征学习的目的，能够在同样的超参条件下迅速达到极佳的性能。IDF 模型针对图数据的结构复杂、节点间信息交互的特点，通过复合多粒度扫描增强了样本特征的拟合优度与多样性，结合加权级联森林的权值策略规则对各子树间的差异给予充分的重视，在一定程度上降低了模型的复杂度且提高了模型分类准确率。相对于DF，实验表明IDF 模型在用于非精确图匹配算法上取得了较好的分类效果。但在扫描选取特征的合理性校检存在不足，在特征的重要程度上如何从重而轻选取，后期会针对相应的问题进一步开展研究。