不平衡数据的Takagi-Sugeno-Kang 模糊分类集成模型

张 壮，王士同

江南大学 人工智能与计算机学院，江苏 无锡 214122

TSK 模型是由Takagi、Sugeno 和Kang 提出的一种模糊模型，它将复杂的非线性问题转化为在不同小线段上的线性问题，使用多个线性子系统拟合一个非线性系统。它由一组if-then 模糊规则来描述，每个规则代表一个子系统，其形式为“ifis，then=()”，其中()是的线性函数。TSK 模糊模型是众多模糊模型之中最具影响力且应用最广泛的一种，它具有高可解释性和强大的逼近能力，已经在很多领域得到了成功的应用。但是，在实践中，模糊模型的性能取决于可用数据的数量和质量，需要充分的训练才能获得较好的泛化能力，而集成学习为构建模型提供了一种有效的方法，它通过结合多个学习器来完成学习任务，通常可以获得比个体学习器更加优越的泛化性能。集成学习可大致分为两类：必须串行生成的Boosting和可以同时并行生成的Bagging与随机森林。在本文中使用Boosting 族算法中最著名的代表AdaBoost，将AdaBoost方法与TSK 模糊模型结合，先从原始数据中训练出一个子模糊模型，再根据子模糊模型的训练效果对训练样本分布进行调整，使得之前子模糊模型训练效果差的样本在接下来的工作中受到更多关注，然后重复进行这一步骤，直到子模糊模型的数量达到预先设置的值，最终将这个子模型结合。AdaBoost 算法可以使TSK 模糊模型得到大量的算法训练，但是如果数据不平衡会导致系统的训练精度下降，泛化能力差。由于少数类样本数量太少，导致模型的准确率更加偏向于多数类，然而现实中存在大量不平衡的数据，如故障检测、疾病诊断等，这些数据训练错误的代价往往是巨大的，因此提高少数类的训练精度至关重要。Chawla 等人提出了合成少数类过采样技术（synthetic minority oversampling technique，SMOTE）方法，它通过添加人工构造的少数类样本来改变原本不平衡数据集的数据分布，减少数据失衡的程度，SMOTE 方法与随机过采样方法的复制样本不同，它通过线性插值的方法合成新样本，对数据集的处理更加有效，缓解了随机过采样引起的过拟合问题，提高了模型在测试集上的泛化性能。

本文通过利用SMOTE 方法处理不平衡的数据集，使类别分布相对均衡，再引入针对TSK 模型的集成方法，形成了训练不平衡数据的集成TSK 模糊模型，不断重复迭代训练获得更好的结果，并且通过改变规则数、模型数量等参数研究模型的性能，提高预测精度。一阶TSK 模糊模型是应用最广泛的模糊模型，为了进一步提高模型的逼近精度，在本文中还将加入二阶模糊模型进行实验。

1 TSK 模糊分类器

TSK 模糊模型是一种以局部线性化为基础，通过模糊推理实现在全局上的非线性的方法，它通过if-then 规则给出非线性系统的局部线性表示，每一条规则代表一个局部线性子系统，一个多输入单输出（multiple input single output，MISO）TSK 模糊模型由条规则组成，其规则如下表示：

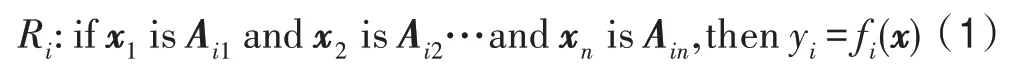
其中，=1,2,…,，是规则数目，R表示模糊模型的第条规则，每一条规则都有与之对应的维输入向量，=[,,…,x]，y是系统输出，A()是规则前件模糊集合，它是输入向量所对应的第条规则的模糊子集，f()为线性函数，采用多项式的形式表示。当f()为一阶线性函数时，对应的模糊模型为一阶模糊模型，如式（2）所示，当f()为二阶线性函数时，对应的模糊模型为二阶模糊模型，如式（3）所示，其中α,α,…,α为规则后件线性参数。

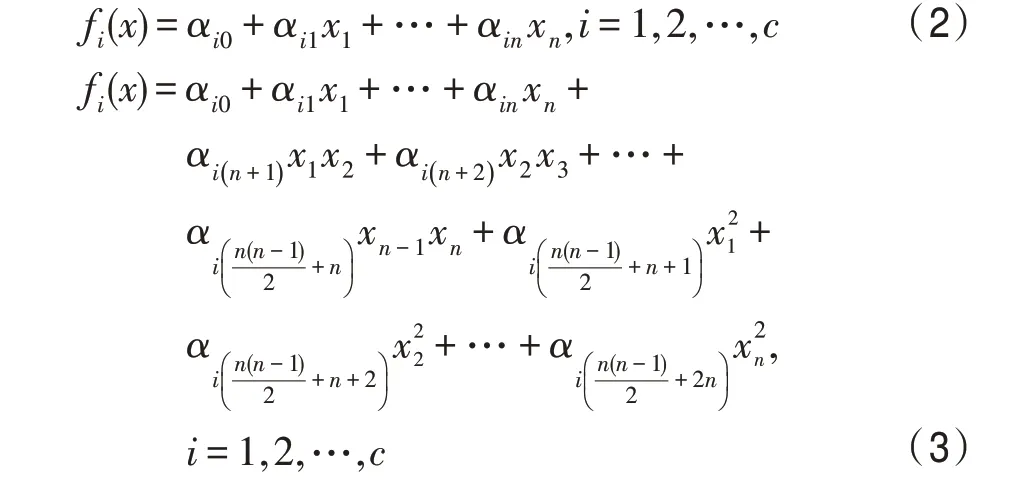
由式（1）可以看到，在TSK 模糊模型中，if-then 规则可以分为两部分：规则前件和规则后件。规则前件对应输入变量在各个子空间的隶属度函数，规则后件则是每个局部子空间的线性函数，TSK 模糊模型的主要任务就是对规则前件参数学习和规则后件参数学习两方面进行研究，下面分别介绍二者的辨识方法。

对规则前件的辨识就是将模糊模型的输入空间划分成一系列的模糊子空间，子空间的划分方法有模糊聚类、模糊搜索树和模糊网格等，最常用的为模糊聚类法。模糊聚类在模糊模型中起着非常重要的作用，通过模糊聚类不仅能得到数据的详细结构，还可以细化模型的功能模块，一般情况下使用模糊C 均值（fuzzy C-means，FCM）算法。FCM 通过优化目标函数，计算每个样本到每个聚类中心的隶属度，再根据隶属度计算聚类中心，不断迭代从而决定一个样本归属于哪个聚类中心。迭代结束后，生成聚类中心，按照式（4）计算规则前件部分的隶属度函数：

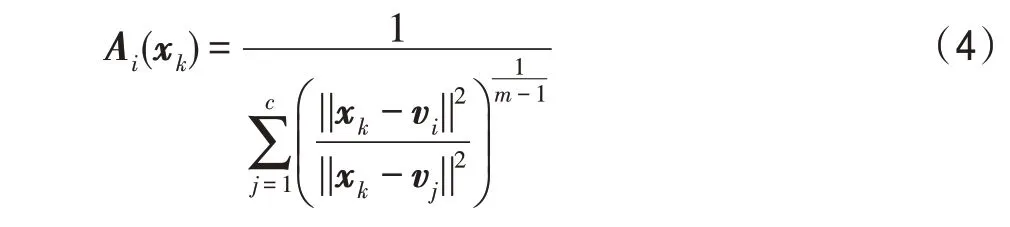
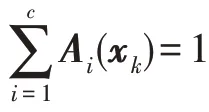
再将式（2）和式（3）代入之后可以得到一阶模型和二阶模型的输出分别为式（6）和式（7）。

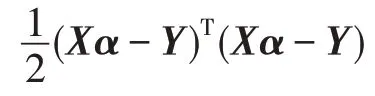
整理之后得：

根据式（9）即可优化得到。

本文将使用TSK 模糊模型处理分类问题，根据训练结果估计某种事物的可能性。例如，对于二分类（0 或1）问题，根据结果更接近0 还是更接近1，判断它属于0 或1 的程度，从而将结果分类。

2 不平衡数据的集成TSK 模糊模型

2.1 模型建立

在基于规则的TSK 模糊模型中，模型的性能取决于可用数据的质量和数量，它需要大量的训练才能获得更好的结果。在这种情况下，集成学习提供了有效的解决办法，使用集成学习构建模型，通过结合不同模型的输出，使得到的模型更加可靠。集成学习结合一组基本学习器，可以将弱小的学习器转化为一个更强大的学习器，预期的模型可能比所有单个模型都要好。在本实验中，使用TSK 模糊模型作为集成学习的基本学习器，根据TSK 模糊模型的表现对样本分布进行调整，重复这一步骤达到预先设定的值。但当集成TSK 模糊模型直接用于不平衡数据集时，其学习性能很容易受到数据集不平衡性的影响，导致集成模型训练精度下降，而在实际应用中，少数类样本的正确识别与多数类样本相比更加具有意义，也通常是研究的重点对象。因此，针对这一问题，本节设计了训练不平衡数据的集成TSK 模糊模型，使用线性插值的方法在两个少数类样本之间人工合成新的样本，以此来降低数据集的不平衡度，降低过拟合的可能性，并通过结合多个学习器来获得更好的性能，提高模型在各种应用场景下的训练效果。

首先，用过采样方法对不平衡数据集预处理，在本研究中采用的过采样方法的思想为：依次取所有少数类样本，搜索其最近邻的个样本（这个近邻都属于少数类样本,一般是奇数，如=5），从这个近邻中随机选择若干个样本作为合成新样本的辅助样本，使用原样本与这些辅助样本进行线性插值，取原样本与其辅助样本的差值，为了确保样本点尽可能得多样化，将这个差值乘以0 到1 之间的随机数，最终可以生成与辅助样本相同数量的合成样本。例如，如果过采样量为原样本的倍，则从个近邻中选择个邻居，每个邻居都可以和原样本一起生成一个新样本。这样，对每一个样本，都生成了个相对应的新样本。若原样本与辅助样本均处于少数类区域，则使用这种方法合成的新样本就是合理的，如果辅助样本属于多数类，则新样本就有可能也属于多数区域，此时的新样本就属于噪声数据影响结果。这种方法是基于随机过采样方法的一种改进算法，随机过采样采取的是简单复制样本的策略，会使得模型学习到的信息过于特别而产生过拟合的问题。而过采样算法是在特征空间中采样的，由于特征空间上邻近的点其特征都是相似的，使用这种方法产生新样本的质量高于传统的随机过采样方法，准确率也更高。

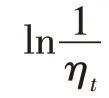
2.2 算法构造

由上节中建立模型的方法可以得到算法结构如图1 所示，先使用过采样算法处理不平衡数据集，再用集成学习训练TSK 模糊模型，算法的步骤如下：

（1）从少数类样本中依次选取每个样本，每次取得的样本记为，计算该样本到少数类样本中其他样本的欧几里德距离，得到样本的个近邻。

（2）设置采样倍率，从的个近邻中随机抽取个样本，将抽取的样本记为x，=1,2,…,。取决于数据的不平衡程度。

（3）将x中的样本分别与原样本进行线性插值操作构建新的样本，构建方式如式（10）所示。其中为新产生的样本，表示0 到1 之间的随机数。

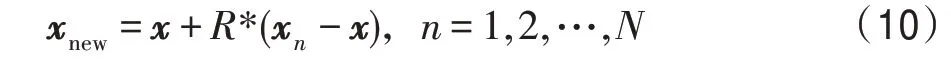
（4）使用新合成的样本与原样本一起组成新的平衡数据集，新数据集的样本个数为。

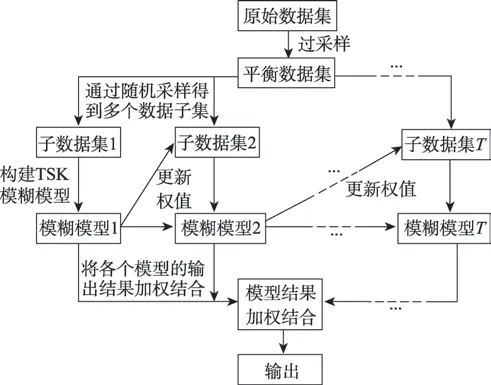
图1 不平衡数据的集成TSK 模糊模型的构建流程Fig.1 Steps of ensemble TSK fuzzy models for imbalanced data

（5）初始化新数据集中所有样本的权值，用表示，=[,,…,w]，初始值全部设置为1/。设置阈值(0 ＜＜1)，设置集成学习中的模型数量和当前迭代次数=1。

（6）根据权值分布对数据集随机采样，组成数据集。

（7）在数据集上使用FCM 算法生成聚类。

（8）在生成的模糊聚类的基础上构建模糊模型作为集成学习的第个子模型，并按照式（6）和式（7）计算模型的预测值Y()。

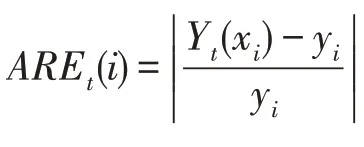
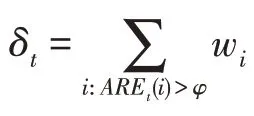
（12）判断是否满足停止条件：若＜，令=+1，并转到步骤（6），否则结束迭代。

（13）计算集成模型的最终输出：

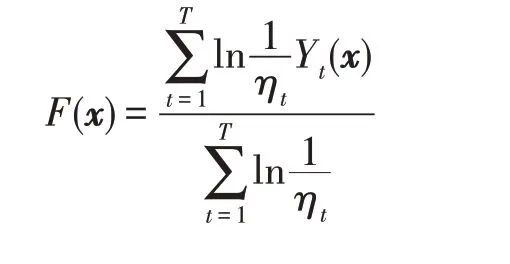
2.3 时间复杂度

算法的时间复杂度主要分为两步，分别对应于算法过程的过采样过程与集成学习两部分。过采样时，若少数类样本数量为，特征数为，采样倍率为，由算法步骤（2）到（3）知，对于每一个样本，都要生成个新样本，且每个新样本都有个特征，需要进行三种循环，每次迭代的复杂度依次为()、()、()，则总的时间复杂度为()。在集成模型中，由步骤（5）知模糊模型数量为，则每次迭代的复杂度依次为()。由步骤（7）和（8）知每次迭代中都要在模糊聚类的基础上构建模糊模型，如果样本数量为，聚类数量为，用表示FCM 算法的迭代次数，则FCM 算法的复杂度为()，再按照式（9）计算规则后件参数，使用式（6）计算模型输出，可得一阶模型的时间复杂度为((+1)+(+1)+(+1))，可化简为()，因此一阶TSK 模型的时间复杂度为(+)，一阶集成TSK 模型的时间复杂度为(+)。同样的，由式（7）得二阶TSK 模型复杂度为(+)，二阶集成TSK 模型为(+)。综上，一阶模型算法总时间复杂度为(++)，二阶模型算法总时间复杂度为(++)，改进后的算法在时间复杂度上的影响较小。

3 实验

为了验证所提出模型的总体性能，本章中对提出的算法在KEEL 数据集网站（http://www.keel.es/）和UCI 数据集网站（http://archive.ics.uci.edu/ml）上的不同数据集进行了实验，这些数据集都为二分类数据集，将被用来比较TSK 模糊模型、集成TSK 模糊模型（ensemble TSK fuzzy models，ETSK）、不平衡数据的集成TSK 模糊模型（ensemble TSK fuzzy models for imbalance data，ETSK-ID）三种模型下的效果。数据集的具体信息如表1 所示。实验中的采样倍率根据数据的不平衡度确定，这些数据集的不平衡程度约为3∶1，则将采样倍率设置为2。

为了保证实验结果的真实准确，每个数据集都采用十折交叉验证，将数据集随机分成10 份，轮流将其中的9 份作为训练数据，1 份作为测试数据进行实验，计算10 次结果的平均值和标准差作为对模型精度的最终结果。将算法中的加权指数设置为2，这是聚类中最常用的值。阈值设置为0.01，如果阈值设置得过低，就很难产生足够数量的正确预测；如果阈值设置得过高，就会只有一些异常的离群值被训练。经过本文的实验，这个阈值在这几个数据集上都能取得较好的效果。而2.1 节中提到权值更新参数取2 为宜，过大或过小都会影响性能。以magic数据集为例，取1、2、3 时的ETSK-ID 均方误差分别为0.115 9、0.114 8、0.120 5。

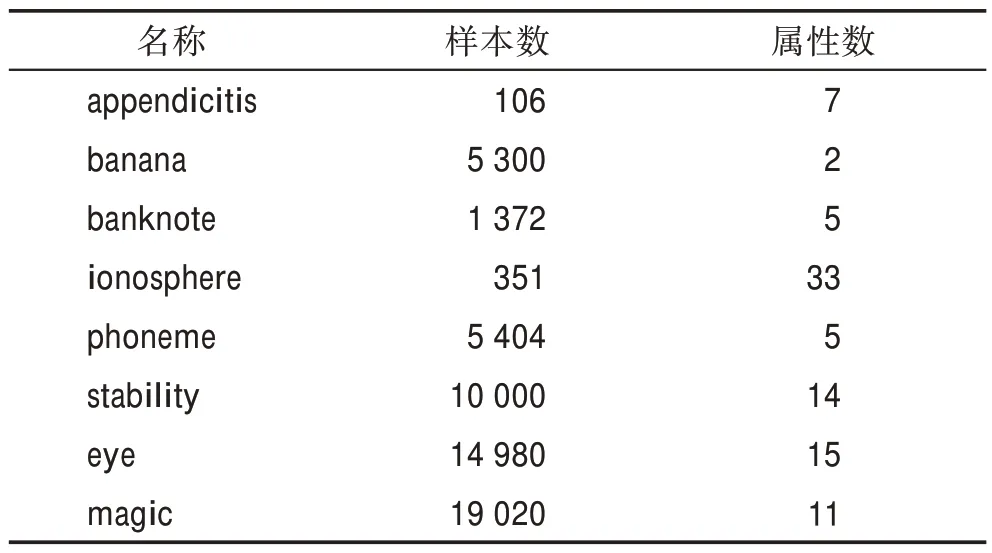
表1 数据集概要Table 1 Summary of datasets

为了说明所提出算法的有效性，在表2 与表3 中分别给出了一阶模型与二阶模型下，TSK、ETSK 和ETSK-ID 三者的均方误差。将规则数量设置为9，使用集成学习时模糊模型的数量选择为6，这样的参数设置下模型通常可以取得足够好的结果，具体的参数设置将在后文中讨论。不仅如此，本文还进一步采用精度作为衡量标准，列举了二阶情况下各模型的对比，结果在表4 中给出。

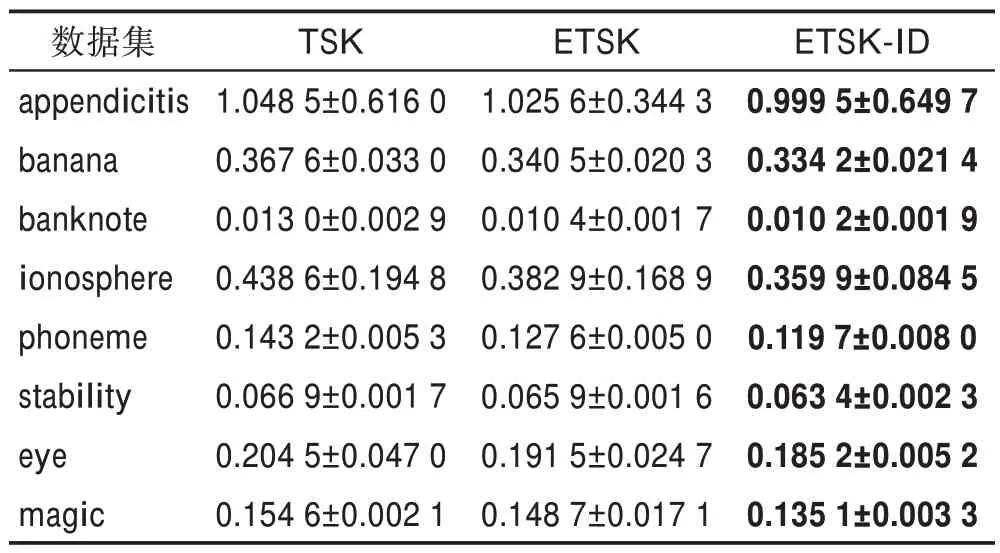
表2 各种一阶模型的均方误差（c=9,T=6）Table 2 MSE obtained for various first-order models (c=9,T=6)

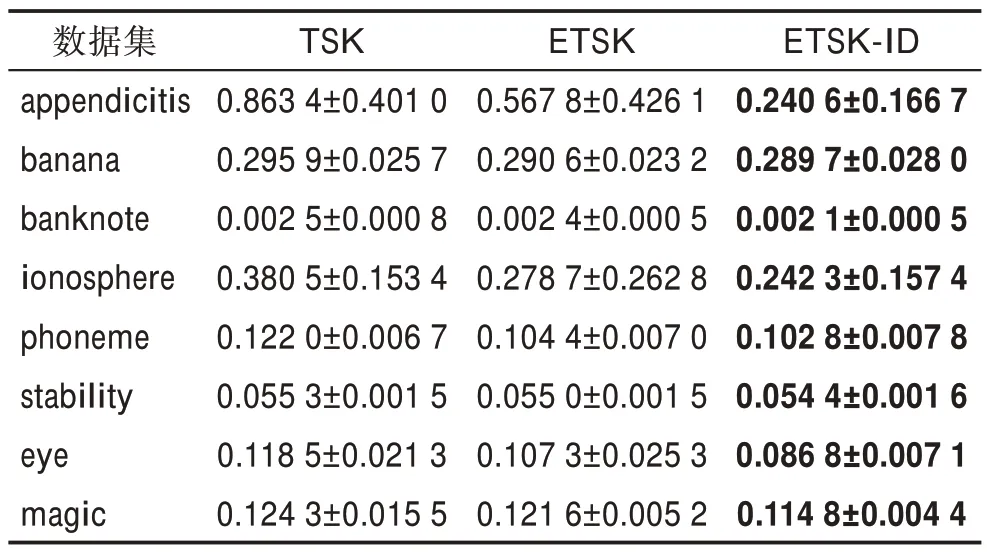
表3 各种二阶模型的均方误差（c=9,T=6）Table 3 MSE obtained for various second-order models(c=9, T=6)

表4 各种二阶模型的精度（c=9,T=6）Table 4 Accuracy obtained for various second-order models (c=9, T=6)%

在图2 中直观展示了使用模型后的提升效果，图左边为一阶模型下TSK、ETSK 和ETSK-ID 的均方误差对比，图右边为二阶模型下TSK、ETSK 和ETSKID 的均方误差对比。可以看到，由于二阶模糊模型中规则后件参数更多，输入属性的数量较多会提升线性函数的性能，使得二阶模糊模型比一阶模糊模型精度更高，且无论是使用一阶模型还是二阶模型，ETSK 都比TSK 性能更好，因为集成学习将多个TSK模糊模型相结合，通常可以获得比单一TSK 模糊模型更加优越的泛化性能，而ETSK-ID 的性能还能进一步提升，这是因为扩充了少数类样本之后，使模型增加了对少数类的偏向，这证明了本文算法在不平衡数据集上的有效性。但banana、banknote 等数据集在二阶模型下过采样之后的性能提升较小，这可能是因为数据集已经得到了比较充分的训练，因此与一阶模型相比波动更小。

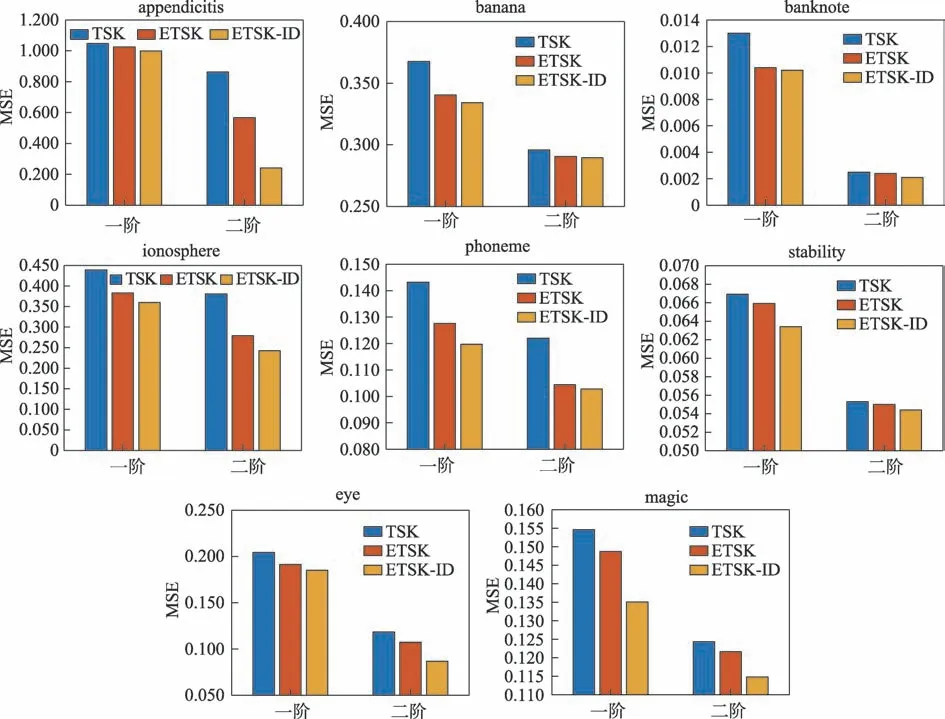
图2 在不同数据集上的模型MSE 值Fig.2 MSE of models on different datasets

模糊模型的优化与FCM 算法中的主要参数有关，即模糊系数和聚类中心，聚类中心与模型中的规则数量相同。一般认为，聚类中心数量越大，模型的准确率越高，但数量太高会导致模型复杂度过高，而在集成学习中，模型数量对模型的性能有最直接的影响。因此，本文将针对规则数和模型数分析二者对模型的影响。

对于ETSK-ID 模型，针对不同数量的子模型寻找最优的结果。由于二阶ETSK-ID 模型的预测精度更高，将详细展示二阶ETSK-ID 模型下参数设置对输出结果的影响。在合适的规则数量（如=9）的前提下，使用不同数量的模糊模型，分别计算它们的均方误差，结果在图3 中给出。在图4 中，再探究规则数对性能的影响，当模型数量设置适当（如=6）时，通过改变规则数量观察它对均方误差大小的影响。

从图3 中可以看到，ETSK-ID 模型中模糊模型的数量较少时，模糊模型的数量对模型性能的影响更加显著，通常模糊模型数量越多，模型性能越好，当模型增加到一定数量之后，模型的均方误差的变化减小，这是因为集成模糊模型随着训练的增加，系统已经较为稳定。再继续提升模型数量，系统性能反而会下降，因为对于加权投票制的集成模型，并不是模型数量越多预测越准确，在本文使用的这些数据集中，最佳的模型数量大约为6 到8。

图4 中的数据表示，一般情况下，ETSK-ID 模型规则数（聚类数）越多，模型精度越高，这是因为聚类越多，聚类的过程就更有能力捕获数据的详细结构。但在一些数据集上，聚类数太大也会导致模型精度降低，因为聚类越多会导致模型越复杂，也会导致规则库的可读性降低。

图3 在不同数据集上模型数量对性能的影响Fig.3 Impact of the number of models on performance on different datasets

图4 在不同数据集上规则数量对性能的影响Fig.4 Impact of the number of rules on performance on different datasets

总之，本文比较了不平衡数据集与过采样之后的平衡数据集在集成模糊模型上的总体性能。首先，采用AdaBoost 集成方法，结合不同的模糊模型来降低单个模型预测的方差，使得模型具有更高的准确性与稳定性。然后，加入SMOTE 过采样算法，让模型更加关注少数类，提高模型在不平衡数据集的精度。实验结果表明，所提出的算法能实现比原始模型更好的性能，平衡的数据集预测效果比不平衡数据集更好，且在一定范围内，随着集成学习中模型数量和TSK 模糊模型中规则数量的增加，模型性能随之提高。这是一个普遍趋势，但这二者过大也会导致预测效果变差，对于模型数量与规则数量，并没有一个确切的数值使系统性能一定会更好，因为性能取决于数据。

4 结束语

本研究使用SMOTE 方法来形成平衡的数据集，再使用针对TSK 模型的集成方法，形成了训练不平衡数据的集成TSK 模糊模型，并报告了一系列实验结果。主要结果表明，对不平衡数据的TSK 模糊集成模型可以获得更好的性能。未来的工作中，仍然有一些问题有待研究，应建立一些其他类型的模糊模型、集成方法和过采样算法，或寻找最优的规则数、模型数和阈值，并在其他的一些领域实施这些模型。