重塑黄土核磁共振T2谱的定量分析与应用

曹雪梅 詹永康 袁磊 舒中潘 张军

摘要：核磁共振技术（NMR）凭借其便捷性、低成本、无损伤的优势被广泛应用于黄土孔隙空间研究领域中。但目前对于重塑黄土核磁共振T2谱的分析应用成果过于单一，从而造成了一定程度上的数据浪费。有鉴于此，基于核磁共振技术，利用数学分析手段对不同干密度重塑黄土的T2谱开展了定量分析;将分析得到的数学参数应用于石油领域中的SDR模型，并构建了重塑黄土的渗透率计算模型。结果表明：① 不同干密度重塑黄土的核磁共振T2谱在数学分析参数（均值、几何均值、标准差以及峰度）中存在不同程度的差异，反映到物理意义上，则是重塑黄土干密度会对土体内部孔隙大小、分布及分选特征产生影响。相比传统的方法仅获取土体孔隙体积，数学统计方法获得的数学参数对孔隙的描述更全面也更精确。② 借助于构建的重塑黄土的SDR模型，求解了试验黄土的渗透率，计算的最小渗透率约为0.3 mD，计算结果与前人总结的规律接近。③ 干密度会影响多个土体微观空间特征，从而引起土体渗透特性的改变。④ 从相关关系方面的分析来看，T2谱的均值和几何均值对土体渗透率影响较大。研究成果在一定程度上可为核磁共振技术在黄土领域中的应用提供新的思路，可为黄土渗透性的预测提供新的方法，也可为了解土体渗透机制提供新的思考。

关 键 词：重塑黄土; 孔隙空间; 核磁共振技术（NMR）; 微观特征; 定量参数

中图法分类号： P66

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.05.033

0 引 言

在中国西北地区，黄土极为重要，分布面积达63万km2，主要分布在山西、陕西、甘肃和宁夏地区[1]。典型黄土是一种具有开放和亚稳定结构的风沙沉积[2]。一些黄土表现出水敏性，在湿润[3]时，由于内部结构塌陷趋于不可控沉降，黄土地基塌陷等岩土工程问题与压实黄土的水分渗流特性密切相关，而作为流体在压实黄土中的流动通道，孔隙空间起着至关重要的作用[4-6]。因此，研究重塑黄土微观孔隙特征，是了解工程中黄土宏观渗透表现的基础。

核磁共振技术（NMR）凭借其便捷性、低成本、无损伤的优势，被广泛应用于研究分析岩土体孔隙空间结构的岩土工程领域，其精确性与稳定性均得到了研究人员的验证。田慧会等[7]利用自由水与结合水冰点不同的特性获取了T2截止值，通过T2截止值得到了T2谱代表的结合水含量。Yuan等[8]通过核磁共振T2谱，研究了不同干密度和干湿循环条件下压实黄土的渗透特性及结构演化。还有大量学者通过核磁共振技术研究了不同岩土体的孔隙特征，进而分析了土体某些宏观表现行为，获得了许多科研成果，效果良好[9-11]。

T2谱作为核磁共振技术的重要成果，可以反映土体内孔隙分布、组成等特点，通过对试样T2谱的特征进行定性与定量分析，可进一步了解重塑黄土孔隙的空间结构。有学者将T2谱与压汞试验相结合，从而提出了非饱和土的渗透系数的预測方法[12];还有学者对T2谱进行了数学分析，将数学参数应用于石油开采率上，从新的角度了解了砂岩储油层中孔隙空间特征[11]。

针对黄土的孔隙结构空间，已有部分学者利用核磁共振技术对其开展了较多的研究[13-14]，但对于T2谱的应用往往仅局限于获取土体孔隙直径大小的分布上，并未对T2谱本身所含有的其他空间信息进行进一步提取，更未进行定量分析，成果应用过于单一，这就使得核磁共振T2谱在黄土领域中的应用不够充分，而且在一定程度上也造成了数据的浪费。

本文基于核磁共振技术获取了不同干密度重塑黄土的T2谱，并利用数学分析手段对其开展了定量分析，并将定量分析得到的数学参数应用到求取不同干密度重塑黄土的渗透率计算模型的构建中。该方法在一定程度上可为核磁共振技术在黄土领域中的应用提供一个新的思路，也可为黄土渗透性的计算提供新的方法;同时，也有助于了解土体的渗透机制。

1 NMR技术原理

核磁共振（NMR）技术是基于H原子的自旋磁性和外加磁场之间的相互作用对舱内试样中的水进行检测的。信号大小与氢原子的个数成正比，与横向磁化矢量的衰减成正比。核磁共振弛豫时间与试样的孔隙半径成正比，这是因为大孔中储水量大，而微孔中储水量小。核磁共振是指在外部磁场作用下能级之间的共振跃迁[15]。在这种磁场下，可以得到偏转后的质子数和质子自转轴恢复到初始平衡态所需要的时间（T2）[16]。

多孔介质的孔隙内部结构、孔隙中的分子运动及其与黄土的反应过程是多孔介质研究领域的重要课题。对于土壤孔隙中的流体，存在3种类型的弛豫机制，即表面流体和自由流体的弛豫、分子的自扩散。因此，孔隙流体流动的弛豫时间T2可表示如下[17]：

1T2=1T2f+1T2s+1T2d（1）

式中：T2为核磁共振横向弛豫时间，ms;T2f为大容器中孔隙流体的弛豫时间，ms;T2s和T2d分别为表面流体弛豫引起的孔隙流体弛豫时间和磁场梯度（ms）扩散引起的孔隙流体弛豫时间。

1T2s=ρ2（SV）（2）

式中：ρ2是横向弛豫系数，取决于土壤性质[17];S/V是孔隙表面积与流体体积的比值。

当只考虑饱和流体时，自由弛豫可以忽略不计，其值比表面弛豫小得多。同时，当磁场均匀且回波时间间隔足够短时，扩散弛豫也可以忽略不计。因此，流体的松弛主要来源于土壤颗粒的表面松弛，式（2） 可近似为[18]

1T2=ρ2（SV）=Fsρ2R（3）

当孔隙为球形时，T2与孔隙半径有关，Fs为孔隙形状因子（当孔隙为圆柱形时Fs=3）。因此，通过式（3）可知核磁共振T2谱线能够反演出土体内部的孔隙空间结构与大小分布特征[13]。

2 试验过程

2.1 试样准备

本次试验所用黄土取自陕西省延安市某挖方边坡，其基本物理性质如表1所列。

依据GB/T 50123-2019《土工试验方法标准》，将土样在108 ℃下烘干24 h，然后碾细后过2 mm筛备用。正如表1所列，试验所用黄土最大干密度为1.8 g/cm3，最优含水量为16.3%，据此本文设置了5种不同干密度（1.80，1.74，1.68，1.62，1.56 g/cm3）的重塑黄土样，为了减少试验偶然误差，另设置1组平行试验。重塑黄土试样含水量均为最优含水量：16.3%。

试样配制时，为了控制制样均匀，首先，将定量散状筛后黄土与相應的蒸馏水混合搅拌均匀，控制含水量为16.3%，用保鲜膜密封静置24 h，待土中水分分布均匀。然后，根据目标干密度计算得到单个试样所需的湿土质量，先后分3层击实进入环刀内，每层土间刮毛防止分层现象。由于核磁共振中磁场较强，传统钢制环刀对其影响较大，本试验中所用环刀为特制聚四氟乙烯材质环刀，聚四氟乙烯可有效消除金属对NMR信号的干扰。按照上述步骤，依次完成了2组5个干密度重塑黄土试样。

2.2 试验过程

采用核磁共振扫描法测量重塑黄土的T2图谱，所用核磁共振仪器型号为MacroMR12-150H-I。该核磁共振仪永久磁铁磁场强度为（0.3±0.05）T，射频发射功率的峰值输出大于300 W，最大线性失真小于0.5%。本次试验所用到的线圈探头的直径为60 mm。

在核磁共振中，要得到能完整反映土体空间结构的T2谱线，试样内孔隙必须要先饱水。所以，首先对聚四氟乙烯内的土样进行饱和，将试样两端用透水石封住，防止土体孔隙在饱和过程中发生改变，也可使饱和过程更加均匀。然后将试样置于真空饱和器中，抽取真空2 h后再进行真空饱和12 h，饱和后立刻进行NMR常温扫描，以获取2组不同干密度重塑黄土的T2图谱。图1为饱和中的试样。

3 核磁共振T2谱图形分布特征

在核磁共振对土体的测试中，首先对试样施加磁场，让土体孔隙中的水的H原子产生共振，然后撤销磁场。由于H原子从共振的状态恢复到激发前的状态时会发出一定的电信号，孔隙越大，恢复到激发前状态的横向弛豫时间也就越久。同一个孔径大小的孔隙越多，体积就越多，产生的电信号也就越强。利用传感器收集这些电信号，然后经过数学反演就得到了T2谱线，横坐标为弛豫时间，其物理意义是孔径大小，弛豫时间越大，代表的孔隙越大。纵坐标是信号强度，某个大小的孔隙越多，其信号强度越强，其物理意义为某个大小孔隙的体积。

接下来，再将纵坐标的信号强度进行归一化，即用单个弛豫时间下的信号强度去除所有弛豫时间下的信号强度的总和，这样就将信号强度转化为了孔隙度分量。最大孔隙度分量约为3%。

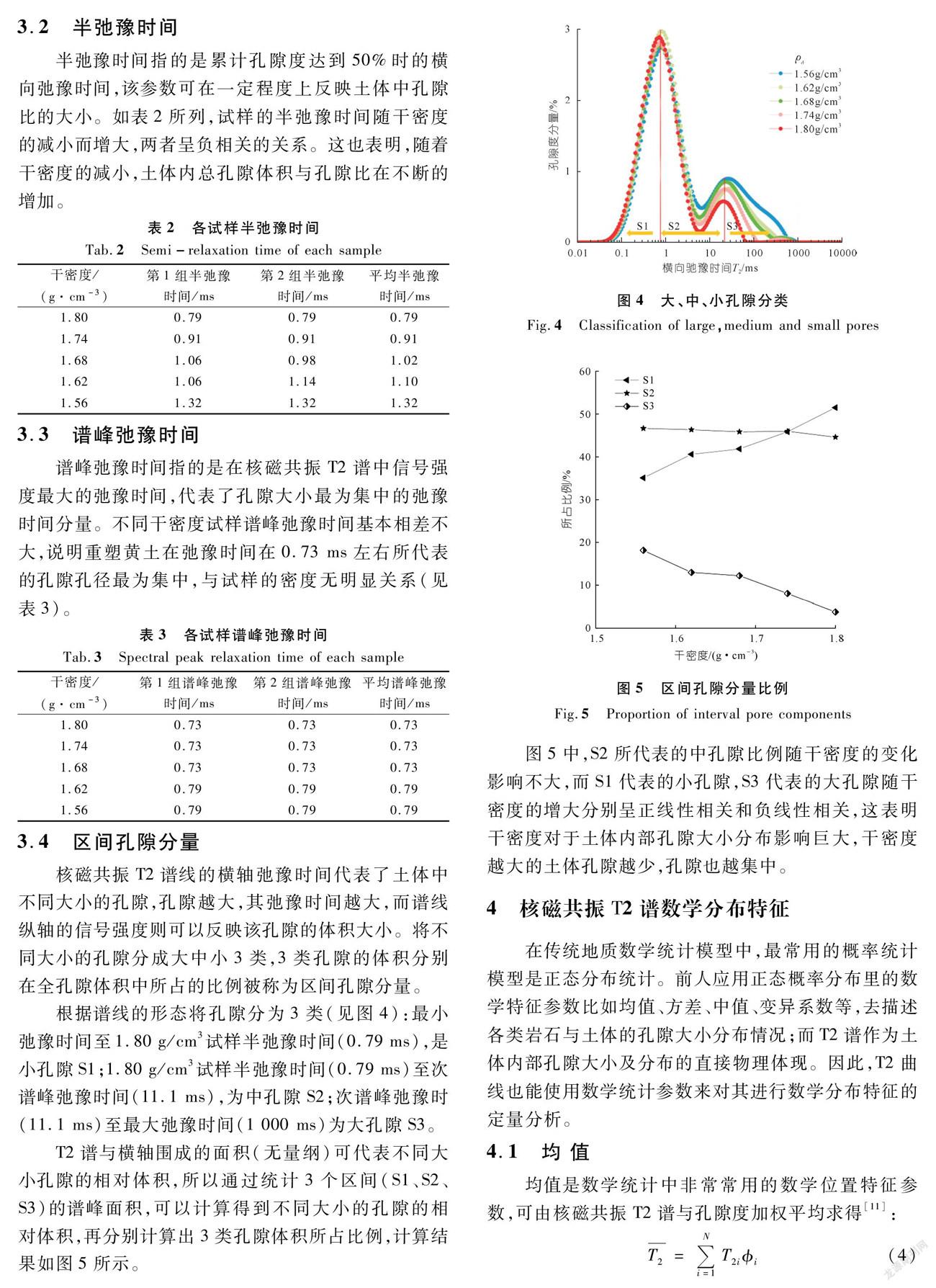
在核磁共振试验中，不同干密度样品的横向弛豫时间T2分布曲线均为双峰分布（见图2），弛豫时间短则代表了小孔隙，弛豫时间长则代表了大孔隙。双峰峰型分布表明重塑黄土体内孔隙具有宏观、中、微观的特征。

根据T2谱的特征可分为图形分布特征与数学分布特征，图形分布特征可用：最大最小弛豫时间、谱峰弛豫时间、区间孔隙分量、最大孔隙度分量和歪度这几个特征参数进行描述，下面依次分析其图形主要特征。

由于2组试样为平行试验，以下参数分析均取这2组试验的平均值。

3.1 最大最小弛豫时间

T2谱中的弛豫时间越大，其代表的孔隙也就越大，因此，最大最小弛豫时间代表了重塑黄土内部最大与最小的孔隙。由图2可知：不同干密度的重塑黄土最小弛豫时间基本一致，为0.01 ms，这是由于仪器本身的限制，所以最小弛豫时间没有对比意义。最大弛豫时间随干密度的增大而减小（见图3），呈现出非线性的趋势。

3.2 半弛豫时间

半弛豫时间指的是累计孔隙度达到50%时的横向弛豫时间，该参数可在一定程度上反映土体中孔隙比的大小。如表2所列，试样的半弛豫时间随干密度的减小而增大，两者呈负相关的关系。这也表明，随着干密度的减小，土体内总孔隙体积与孔隙比在不断的增加。

3.3 谱峰弛豫时间

谱峰弛豫时间指的是在核磁共振T2谱中信号强度最大的弛豫时间，代表了孔隙大小最为集中的弛豫时间分量。不同干密度试样谱峰弛豫时间基本相差不大，说明重塑黄土在弛豫时间在0.73 ms左右所代表的孔隙孔径最为集中，与试样的密度无明显关系（见表3）。

3.4 区间孔隙分量

核磁共振T2谱线的横轴弛豫时间代表了土体中不同大小的孔隙，孔隙越大，其弛豫时间越大，而谱线纵轴的信号强度则可以反映该孔隙的体积大小。将不同大小的孔隙分成大中小3类，3类孔隙的体积分别在全孔隙体积中所占的比例被称为区间孔隙分量。

根据谱线的形态将孔隙分为3类（见图4）：最小弛豫时间至1.80 g/cm3试样半弛豫时间（0.79 ms），是小孔隙S1;1.80 g/cm3试样半弛豫时间（0.79 ms）至次谱峰弛豫时间（11.1 ms），为中孔隙S2;次谱峰弛豫时（11.1 ms）至最大弛豫时间（1 000 ms）为大孔隙S3。

T2谱与横轴围成的面积（无量纲）可代表不同大小孔隙的相对体积，所以通过统计3个区间（S1、S2、S3）的谱峰面积，可以计算得到不同大小的孔隙的相对体积，再分别计算出3类孔隙体积所占比例，计算结果如图5所示。

图5中，S2所代表的中孔隙比例随干密度的变化影响不大，而S1代表的小孔隙，S3代表的大孔隙随干密度的增大分别呈正线性相关和负线性相关，这表明干密度对于土体内部孔隙大小分布影响巨大，干密度越大的土体孔隙越少，孔隙也越集中。

4 核磁共振T2谱数学分布特征

在传统地质数学统计模型中，最常用的概率统计模型是正态分布统计。前人应用正态概率分布里的数学特征参数比如均值、方差、中值、变异系数等，去描述各类岩石与土体的孔隙大小分布情况;而T2谱作为土体内部孔隙大小及分布的直接物理体现。因此，T2曲线也能使用数学统计参数来对其进行数学分布特征的定量分析。

4.1 均 值

均值是数学统计中非常常用的数学位置特征参数，可由核磁共振T2谱与孔隙度加权平均求得[11]：

T2=Ni=1T2ii（4）

式中：i为第i个弛豫时间对应的核磁共振孔隙度分量;

T2i为第i个弛豫时间，ms。

由式（4）可求得各重塑黄土试样的T2谱的均值，能反映全孔隙中的平均孔隙大小。由表4可以看出：试样T2谱均值随干密度的减小而增大，呈负线性相关关系。

4.2 幾何均值

几何均值和均值都是求一组数据中平均值的方法[19]，而几何均值则更多用于数据的平均增长率的研究中。几何均值可由下式定义[20]：

T2gm=（∏Ni=1T2i）i（5）

式中：T2gm为T2的几何均值;

i为第i个弛豫时间对应的核磁共振孔隙度分量;

T2i为第i个弛豫时间，ms。

按式（5）求得每组试样的几何均值。各试样T2谱几何均值如表5所列。

几何均值随干密度的增大而减小，呈负相关关系，表明重塑黄土的干密度越大，T2曲线的平均增长率越小。

4.3 标准差

标准差是描述离均差平方的算术平均数。在孔隙系统中，可用于描述孔隙体积大小的分选性，标准差越小，说明孔隙大小的分选性越好，孔隙大小越集中。可由下式计算：

σ=（iT2i-T2）2（6）

式中：σ为标准差;

i为第i个弛豫时间对应的核磁共振孔隙度分量;

T2i为第i个弛豫时间，ms;

T2为均值;

为均值对应的孔隙度分量。

按式（6）求得每组试样的标准差。各试样T2谱标准差如表6所列。

标准差随干密度的增大而减小，呈负相关关系，表明干密度越大的重塑黄土，其内部孔隙分选性越好，孔隙大小越集中在某个孔径区间。

4.4 变异系数

标准差与均值的比值被称为变异系数，是对数据值相对变化的体现。变异系数越小，孔隙结构、分选性也就越好。其计算式为

C=σ/T2（7）

按式（7）求得每组试样的变异系数。各试样T2谱变异系数如表7所列。

从表7可以得知：不同干密度试样核磁共振T2谱的变异系数基本一致，说明干密度的大小并不会影响重塑黄土内部变异系数。

4.5 峰 度

峰度在核磁共振中是用来衡量T2谱曲线的陡峭程度，可以反映重塑黄土内部不同大小孔隙的集中程度，是用来评价孔隙结构很好的一个定量参数，计算公式如下：

KG=（2iT2i-T2）4σ4（8）

按式（8）求得每组试样的峰度。各试样T2谱峰度如表8所列。

由表8可以看出：峰度大致随干密度增大而增大，表明干密度越大，T2曲线越陡，孔隙越集中。

5 定量参数分析与应用

5.1 定量参数分析

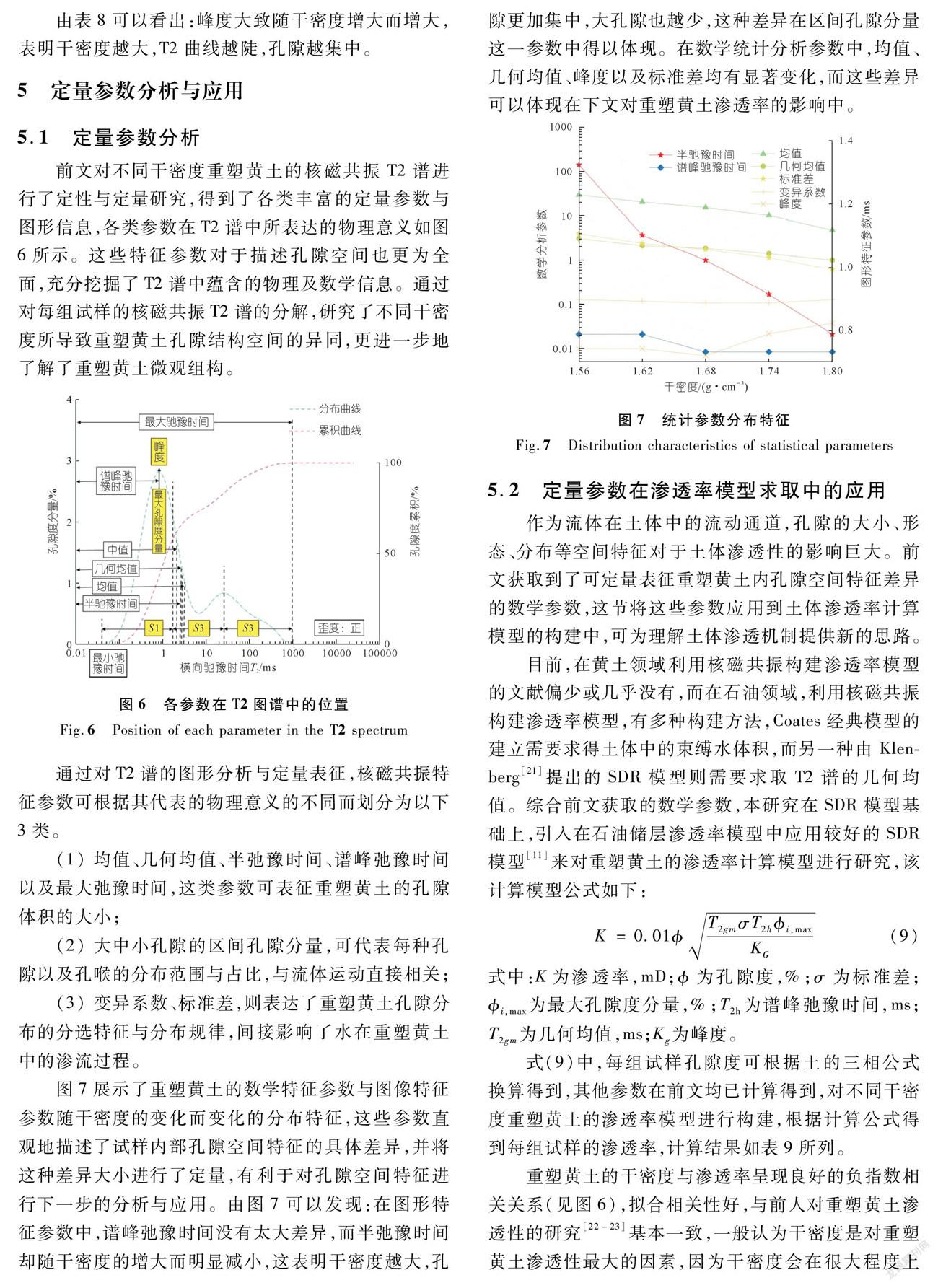
前文对不同干密度重塑黄土的核磁共振T2谱进行了定性与定量研究，得到了各类丰富的定量参数与图形信息，各类参数在T2谱中所表达的物理意义如图6所示。这些特征参数对于描述孔隙空间也更为全面，充分挖掘了T2谱中蕴含的物理及数学信息。通过对每组试样的核磁共振T2谱的分解，研究了不同干密度所导致重塑黄土孔隙结构空间的异同，更进一步地了解了重塑黄土微观组构。

通过对T2谱的图形分析与定量表征，核磁共振特征参数可根据其代表的物理意义的不同而划分为以下3类。

（1） 均值、几何均值、半弛豫时间、谱峰弛豫时间以及最大弛豫时间，这类参数可表征重塑黄土的孔隙体积的大小;

（2） 大中小孔隙的区间孔隙分量，可代表每种孔隙以及孔喉的分布范围与占比，与流体运动直接相关;

（3） 变异系数、标准差，则表达了重塑黄土孔隙分布的分选特征与分布规律，间接影响了水在重塑黄土中的渗流过程。

图7展示了重塑黄土的数学特征参数与图像特征参数随干密度的变化而变化的分布特征，这些参数直观地描述了试样内部孔隙空间特征的具体差异，并将这种差异大小进行了定量，有利于对孔隙空间特征进行下一步的分析与应用。由图7可以发现：在图形特征参数中，谱峰弛豫时间没有太大差异，而半弛豫时间却随干密度的增大而明显减小，这表明干密度越大，孔隙更加集中，大孔隙也越少，这种差异在区间孔隙分量这一参数中得以体现。在数学统计分析参数中，均值、几何均值、峰度以及标准差均有显著变化，而这些差异可以体现在下文对重塑黄土渗透率的影响中。

5.2 定量参数在渗透率模型求取中的应用

作为流体在土体中的流动通道，孔隙的大小、形态、分布等空间特征对于土体渗透性的影响巨大。前文获取到了可定量表征重塑黄土内孔隙空间特征差异的数学参数，这节将这些参数应用到土体渗透率计算模型的构建中，可为理解土体渗透机制提供新的思路。

目前，在黄土领域利用核磁共振构建渗透率模型的文献偏少或几乎没有，而在石油领域，利用核磁共振构建渗透率模型，有多种构建方法，Coates经典模型的建立需要求得土体中的束缚水体积，而另一种由Klenberg[21]提出的SDR模型则需要求取T2谱的几何均值。综合前文获取的数学参数，本研究在SDR模型基础上，引入在石油储层渗透率模型中应用较好的SDR模型[11]来对重塑黄土的渗透率计算模型进行研究，该计算模型公式如下：

K=0.01T2gmσT2hi，maxKG（9）

式中：K为渗透率，mD;

为孔隙度，%;

σ为标准差;

i，max为最大孔隙度分量，%;

T2h为谱峰弛豫时间，ms;

T2gm为几何均值，ms;

Kg为峰度。

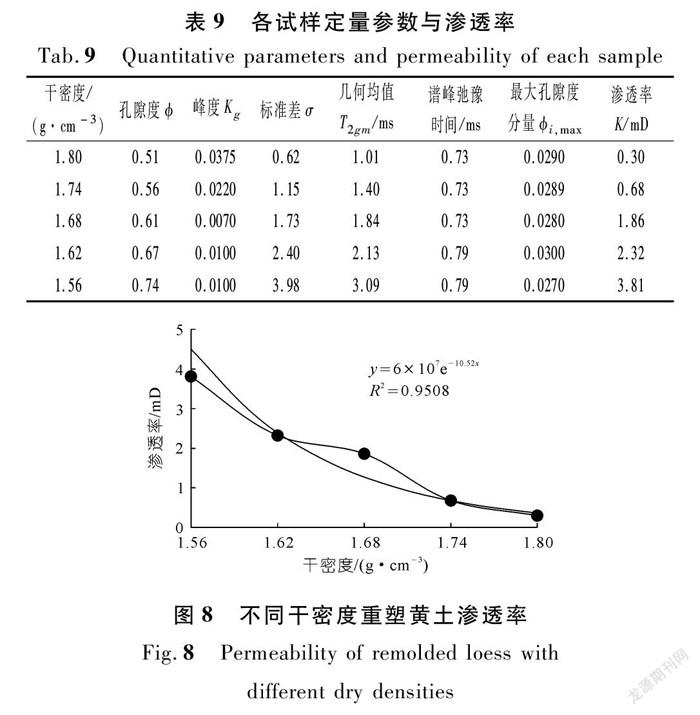
式（9）中，每组试样孔隙度可根据土的三相公式换算得到，其他参数在前文均已计算得到，对不同干密度重塑黄土的渗透率模型进行构建，根据计算公式得到每组试样的渗透率，计算结果如表9所列。

重塑黄土的干密度与渗透率呈现良好的负指数相关关系（见图6），拟合相关性好，与前人对重塑黄土渗透性的研究[22-23]基本一致，一般认为干密度是对重塑黄土渗透性最大的因素，因为干密度会在很大程度上改变土体内部孔隙空间结构，导致流体在流动通道内的运动过程发生改变，从而引起渗透特性的变化。

6 结 论

基于核磁共振技术，获取了不同干密度重塑黄土的T2谱;并利用数学分析手段对其进行定量分析，将定量分析得到的数学参数应用于构建重塑黄土的渗透率计算模型中，探索了一套T2谱在黄土孔隙空间分析中应用的新思路。可以得出以下主要结论。

（1） 利用数学统计手段对核磁共振T2谱进行定量分析，可以更直观与更精确地分析不同试样间的孔隙空间差异。不同干密度重塑黄土的核磁共振T2谱在数学统计参数中存在不同程度的差异，这些差异反映到物理意义上则是：重塑黄土干密度不同会对土体内部孔隙大小、分布及分选特征产生影响，这些影响的大小则均可通过参数的数值差异进行更为准确的定量表达。相比传统仅获取土体孔隙体积，数学统计方法获得的数学参数对孔隙的描述更全面与精确。

（2） 将石油领域中SDR模型引入到了重塑黄土的渗透率模型的构建中，得到了重塑黄土的渗透率模型;并根据模型求取了不同干密度重塑黄土的渗透率。根据模型计算得到试样黄土的渗透率为0.30～3.81 mD。其次，干密度会导致土体渗透特性的改变：干密度越大，渗透率越低，且呈负指数的相关关系。另外，模型还反映了不同微观孔隙特征参数对土体渗透率的贡献大小，进一步理解了干密度变化导致土体渗透率变化的微观因素。模型计算结果与前人获得规律相似度高，这表明本文研究方法可信度较高，可行性较好。

本文研究成果在一定程度上可为核磁共振在黄土领域中的应用提供新的思路，可为黄土渗透性的预测提供新的方法，更可为了解土体渗透机制提供新的思考，具有较高的理论创新性与应用实用性。

参考文献：

[1] 王数.地质学与地貌学[M].北京：中国农业大学出版社，2013.

[2] ROLLINS K M，ROGERS G M.Mitigation measures for small structures on collapsible alluvial soils[J].Journal of Geotechnical Engineering，1994，120（9）：1533-1553.

[3] ASSALLAY A M，ROGERS C D F，SMALLEY I J.Formation and collapse of metastable particle packings and open structures in loess deposits[J].Engineering Geology，1997，48（1-2）：101-115.

[4] SIRVITHAYAPAKORN S，KELLER A.Transport of colloids in saturated porous media：A pore-scaleobservation of the size exclusion effect and colloid acceleration[J].Water Resources Resarch，2003，39（4）：1109-1120.

[5] 李鹏举，谷宇峰.核磁共振T2谱转换伪毛管压力曲线的矩阵方法[J].天然气地球科学，2015，26（4）：700-705.

[6] 刘勇健，李彰明，郭凌峰，等.基于核磁共振技术的软土三轴剪切微观孔隙特征研究[J].岩石力学与工程学报，2018，37（8）：1924-1932.

[7] 田慧会，韦昌富.基于核磁共振技术的土体吸附水含量测试与分析[J].中国科学：技术科学，2014，44（3）：295-305.

[8] YUAN K Z，LU X F，WANG X J.Permeability characteristics and structural evolution of compacted loess under different dry densities and wetting-drying cycles[J].PLoS ONE，2021，16（6）：e0253508.

[9] 運华云，赵文杰，刘兵开，等.利用T2分布进行岩石孔隙结构研究[J].测井技术，2002，26（1）：18-21，89.

[10] 李海波，朱巨义，郭和坤.核磁共振T2谱换算孔隙半径分布方法研究[J].波谱学杂志，2008，25（2）：273-280.

[11] 白松涛，程道解，万金彬，等.砂岩岩石核磁共振 T2谱定量表征[J].石油学报，2016，37（3）：282-391.

[12] 陈银.基于核磁共振技术的非饱和土渗透系数预测方法[D].武汉：湖北工业大学，2019.

[13] 何攀，许强，刘佳良，等.基于核磁共振技术的结合水含量对重塑黄土抗剪强度影响试验研究[J].山地学报，2020，38（4）：571-580.

[14] 杨更社尤，吴迪.冻融环境下原状黄土孔径分布与其力学特性关系的试验研究[J].煤炭工程，2019，51（3）：107-112.

[15] SCHAUMANN G E.Proton nuclear magnetic resonance（NMR）relaxometry in soil science[J].Encyclopedia of Agrophysics，2011：543-669.

[16] CONTE P，STEFANO C D，FERRO V，et al.Assessing hydrological connectivityinside a soil by fast-fieldcycling nuclear magnetic resonance relaxometry and its link to sediment delivery processes[J].Environ.Earth Sci.，2017，76：526.

[17] XU J，LI Y，REN C，et al.Damage of saline intact loess after dry-wet and its interpretation based on SEM and NMR[J].Soils and Foundations，2020，60（4）：911-928.

[18] 何雨丹，毛志強，肖立志.核磁共振T2分布评价岩石孔径分布的改进方法[J].地球物理学报，2005，48（2）：373-378.

[19] 何更生，唐海.油层物理[M].2 版.北京：石油工业出版社，2011.

[20] 杨正明，李治硕，王学武，等.特低渗透油田相对渗透率曲线测试新方法[J].石油学报，2010，31（4）：629-632.

[21] KLEINBERG R L.Utility of NMR T2 distributions，connection with capillary pressure，clay effect，and determination of the surface relaxivity parameter ρ2[J].Magnetic Resonance Imaging，1996，14（7-8）：761-767.

[22] 高燕燕.重塑黄土的渗透特性研究[D].西安：长安大学，2016.

[23] 高文静.细粒土渗透特性的影响因素试验研究[D].西安：西安理工大学，2018.

（编辑：赵秋云）

Quantitative analysis on NMR T2 spectrum in remolded loess and application

CAO Xuemei1，ZHAN Yongkang2，YUAN Lei3，SHU Zhongpan4，ZHANG Jun4

（1.Sichuan Vocational and Technical College of Communications，Chengdu 611130，China; 2.Sichuan Aba Traffic Construction Investment Co.，Ltd.，Aba 624000，China; 3.Transportation Bureau of Aba Tibetan and Qiang Autonomous Prefecture，Aba 624000 ，China; 4.Sichuan Institute of Geological Engineering Investigation Group Co.，Ltd.，Chengdu 610072 ，China）

Abstract：

Nuclear Magnetic Resonance （NMR） is widely used in the analysis of pore space characteristics of loess due to its convenience，low cost，and no damage.However，the previous analysis and application of remolded loess T2 spectrum were limited to obtaining the distribution of pore size，and other spatial information contained in the T2 spectrum was not further extracted，which made the application results of the NMR T2 spectrum too single，resulting in a certain degree of data waste.Based on this，we used mathematical analysis method to quantitatively analyze the T2 spectrum of remolded loess with different dry densities，and applied the mathematical parameters obtained by quantitative analysis to the SDR model，so as to construct a permeability calculation model for remodeled loess.The main conclusions were as follows：（1） There are various differences in the statistical analysis parameters （mean，geometric mean，standard deviation and kurtosis） of the NMR T2 spectrum of loess remolded with different dry densities，which has physical meanings：different dry densities of remolded loess will affect the size，distribution and sorting characteristics of pores in the soil.Compared with the traditional method to obtain the pore volume of soil，the mathematical parameters obtained by numerical statistics method can describe the empty pores more comprehensively and accurately.（2） The permeability of each remolded loess was calculated by constructing the SDR model of the remolded loess，the minimum permeability was about 0.3 mD，and the calculated results were close to the previous experimental results.（3） Dry density affected micro-spatial characteristics of soil，and causing the change of soil permeability characteristics.（4） From the correlation analysis，the mean and geometric mean of T2 spectrum had great influence on soil permeability.To a certain extent，the research results can provide new ideas for the application of NMR in the loess study field，new methods for predicting the permeability of loess，and new thinking for understanding the mechanism of soil permeability.

Key words：

remolded loess;pore space;Nuclear Magnetic Resonance （NMR）;microscopic characteristics;quantitative parameters