一类三维结合代数的分类*

李 军，温永琪

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

在信息、控制、工程等应用领域中,会出现大量的行、列或对角线的对称图像(矩阵).邹红星等在研究谱线增强[1]时发现,利用短时Fourier变换的对称性可以显著减少矩阵的奇异值分解所需的计算量及存储量.进而,他提出了行(或列)对称矩阵的概念,并讨论了它们的奇异值分解等问题(见文献[2-3]).随后,袁晖坪等人研究了行(或列)及行列对称矩阵的相应性质及相关的矩阵分解(见文献[4-8]).本文首先证明了实数域上的n阶行列对称矩阵全体构成一个半单的结合代数.而对于低维结合代数的分类问题,一直是研究者们广泛关注的一个课题(见文献[9-16]).本文利用Kobayashi.Y等人给出的实数域上三维结合代数的具体分类[9],用5阶行列对称矩阵形式给出了实数域上由行列对称矩阵构成的含单位元的三维结合代数的分类结果.

1 记号和预备知识

定义1设A是实数域上的线性空间,在A中定义了乘法运算,称A为实数域上的结合代数,当A满足∀a,b,c∈A,k∈,有

如果存在元素e∈A,∀a∈A,ea=ae=a,则e是A的单位元,A叫做含单位元的结合代数.设b∈A,记CA(b)={a∈A∣ab=ba},称为A中关于b的中心化子.令Mn()为实数域上的n阶矩阵全体构成的结合代数.令

为单位反对角矩阵,En为n阶单位矩阵.

定义2[4]设a=(aij)∈Mn()，称

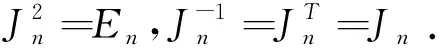
引理1[9]设U为实数域上含单位元e的三维结合代数,令e,a,b为U的一组基,则在同构意义下,结合代数U仅有以下6种情形：

2 行列对称矩阵构成的结合代数

定理1设RCSn()为实数域上的n阶行列对称矩阵全体构成的结合代数,则RCSn()是一个半单代数.特别地,

证明RCSn()={a∈Mn()∣aJn=Jna}=CMn()(Jn),而Jn为实数域上的对称矩阵,因此存在实数域上的n阶可逆矩阵t使得t-1Jnt为实对角矩阵,令Λ=t-1Jnt.由可知,Λ2=En.可得t-1RCSn()t=t-1CMn()(Jn)t=CMn()(Λ).令则f2=f为幂等元.易证对于任意a∈Mn(),aΛ=Λa当且仅当af=fa.因此,CMn()(Λ)=CMn()(f).这里,若n=2k(k∈)为偶数时,则此时,从而RCSn()作为结合代数同构于若n=2k+1(k∈)为奇数时,则有因此RCSn()作为结合代数同构于得证.

由定理1可知,RCSn()有一个直和分解,当n=2k(k∈)为偶数时,RCSn()≅Mk()⊕Mk();当n=2k+1(k∈)为奇数时,RCSn()≅Mk+1()⊕Mk().特别地,当n=5时,RCS5()≅M3()⊕M2().

定理2设A为实数域上由行列对称矩阵构成的含单位元的三维结合代数,则在同构意义下,结合代数A仅有以下6种情形：

证明设三维结合代数A的一组基为e,a,b,其中e为A的单位元.容易验证A0,A1,A2,A3,A4,A5为由行列对称矩阵构成的含单位元的三维结合代数.对于结合代数A0,取e为5阶单位矩阵,

由e,a,b共同构成了三维结合代数A0的一组基.通过计算可得a2=a,b2=b,ab=ba=0.由其乘法表可知A0≅U0.类似地,通过在A1,A2,A3,A4,A5中容易找到合适的一组基e,a,b,由结合代数的乘法表可同理证得,A1≅U1,A2≅U2,A3≅U3,A4≅U4,A5≅U5.而在同构意义下,由引理1可知,实数域上的含单位元的三维结合代数有且仅有这6种情形,得证.