林芝市公路地质灾害易发性区划及气象预报模型

陶星宇, 柳锦宝, 黄志刚, 巴 桑, 卓 玛, 陈 军, 肖 斌, 高瑜莲, 费晓燕

(1.成都信息工程大学 资源环境学院, 四川 成都 610225; 2.福建省气象服务中心,福建 福州 350001; 3.西藏高原大气环境科学研究所, 西藏 拉萨 850000; 4.西藏自治区气候中心,西藏 拉萨 850000; 5.北京师范大学 地理学部, 北京 100875; 6.四川公众项目咨询管理有限公司, 四川 成都 610051)

林芝市境内主要公路大多分布于河流两侧的阶地上，使得因强降水引起的地质灾害的威胁以冲毁公路为主，其中，降水诱发的滑坡、崩塌、泥石流是林芝市地质灾害中威胁、损失最大的灾种[1]。截止到2019年，通过市县地质灾害调查与区划查明的地质灾害点约152处，隐患点约1 213处，而由降水诱发的地质灾害占全市各类地质灾害总数的80%，几乎每年都会发生几十次不同程度、不同规模的地质灾害，造成重大损失。近年来，地质灾害的发生愈加频繁，造成的经济损失越来越重，2016年10月11日，林芝市易贡茶场白龙沟发生大型泥石流地质灾害，造成直接经济损失2 154.59万元；2018年10月17日，雅鲁藏布江林芝市米林县加拉村段发生滑坡地质灾害，造成直接经济损失118 158.94万元。在汛期，林芝市大部分地质条件比较复杂的路段往往会发生滑坡、崩塌、泥石流等严重的地质灾害，对沿线交通设施、群众的生命安全构成严重的威胁。因此，加强林芝市公路沿线地质灾害防治及气象预报工作具有重要意义。

预报模型是成功开展地质灾害气象预报的基础，近年来，地质灾害气象预报模型的研究得到了国内外学者及政府的高度重视[2-7]，刘传正等[8]针对三峡库区建立了降水判据模型，提出了地质灾害预报与防治措施，给地质灾害预报研究提供了新方向；Keiko[9]基于多元线性回归法对诱发地质灾害的降水量因子进行了分析[9]，这种只考虑降水量而未考虑到地质灾害背景条件的阈值模型，结果差异很大，实际应用受到限制[10-14]。因此，对地质背景与降水量相结合的预报模型开始了研究，在多因子模型的基础上，浙江、贵州、江苏、广东、四川、广西、甘肃等省开始构建了地质灾害气象预报系统[15-21]；费晓燕、陈宫燕等[22-23]结合降水资料和地质环境特征，基于逻辑回归方法分别对四川省和林芝市进行地质灾害气象预报研究。而现在国内大多研究的是大范围地质灾害气象预报，小范围预报和服务对象等方面考虑较少[24-25]，对于构建小范围公路地质灾害气象预报模型方面的研究更是少之又少。目前，陈洪凯等[26]选取了暴雨、温度、植被覆盖率、灾害体、年均降水量、岩性条件、路基位置、地震烈度、地貌类型、地质构造等10个因子，针对川藏公路提出了地质灾害危险性区划模型；孟兆兴等[27]基于信息量法、逻辑回归模型及空间逻辑回归模型对川藏公路进行了易发性评价。目前，对于公路沿线地质灾害的研究主要集中在易发性评价方面，未结合降水量因子进行分析，无法进行地质灾害预报服务。因此，本研究则在地质灾害易发性评价的基础上，进一步进行地质灾害气象预报模型研究。本研究通过建立林芝市公路沿线15 km缓冲区，对林芝市公路沿线地质灾害易发性区划和降水诱发地质灾害关系进行研究，构建林芝市公路沿线地质灾害气象预报模型，为实施林芝市境内公路地质灾害气象预报提供了依据。

1 研究区概况

本研究以林芝市公路沿线15 km缓冲区为研究区，林芝市位于西藏自治区的东南部喜马拉雅山脉中段，南靠冈底斯山脉，北傍念青唐古拉山，地处雅鲁藏布江中下游，属高山峡谷区，山高谷深，土质基本为沙壤结构，森林覆盖率为46%，是中国第三大林区。研究区内主要为山地地貌与河谷、山间盆地侵蚀堆积地貌区，地形完整性差，地形起伏大，平均海拔3 000 m，最低点海拔155 m，是陆地垂直地貌落差最大的地区。同时，该区域是强烈的构造隆起区与不同的地质构造区的交汇地带[28]，该研究区属于藏东南地区强烈的挤压带，包括喜马拉雅板片、雅鲁藏布江缝合带、冈底斯—念青唐古拉板块、班公错—怒江缝合带、羌塘—三江复合板块、金沙江缝合带[29-30]。研究区内均发育有各个时代的地层，岩石类型分布复杂，主要有泥盆系、三叠系的板岩、片岩、片麻岩、大理岩以及侏罗纪的泥岩等[31]。受印度洋暖流与北方寒流的影响，形成了热带、亚热带、温带和寒带并存的复杂气候带，年降水量达到650 mm左右，降水多且集中。对研究区内2010—2019年日降水量数据进行年均月降水量统计分析，由于2015年气象站点数据较少，不具备典型性，则将其剔除，剔除后发现5—9月(主汛期)的年均月降水量较大，其中，7月最大，年均月降水量达到了4 055 mm。因此，在地形地貌、地质构造、地层岩性和降水等因素的共同作用下使得林芝市成为西藏自治区地质灾害最严重的地区，其中，2010—2019年研究区灾害点及隐患点分布如图1所示。

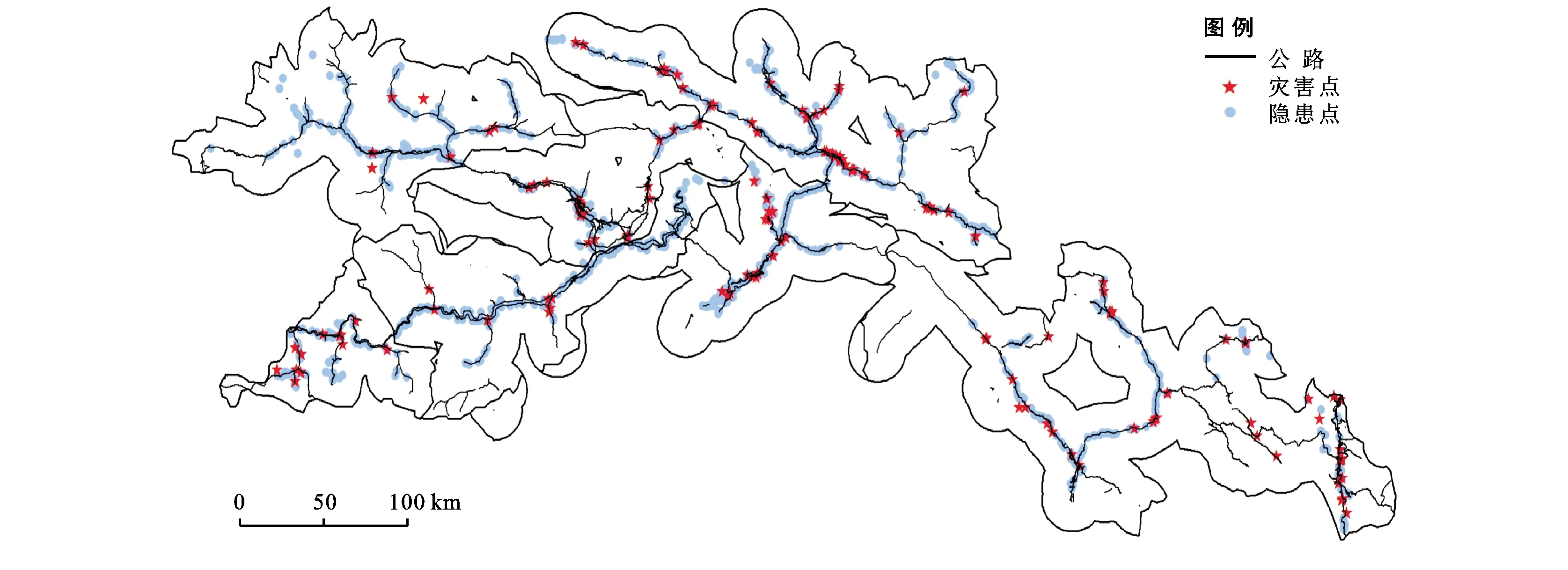
图1 林芝市公路沿线灾害点及隐患点分布

2 研究数据及方法

2.1 数据来源

本研究中使用的数据主要包括Landsat 8影像、DEM数据、土地利用、土壤、降水量、河流、道路、断层、地质灾害点及隐患点等数据。其中，Landsat 8影像源于美国地质勘探局官网USGS(https:∥earthexplorer.usgs.gov/)；DEM数据源于NASA官网(https:∥www.nasa.gov/)SRTM1 30 m数字高程数据；土地利用数据源于NASA官网2018年MOD12Q1产品数据；土壤类型数据源于《1∶100万中华人民共和国土壤图》；河流、道路数据源于Open Street Map官网(https://www.openstreetmap.org/)；断层数据源于全国地质信息资料网(http://www.drc.cgs.gov.cn)全国1∶250万地质数据；降水量、地质灾害点及隐患点数据由林芝市气象局及自然资源局提供，时间段为2010—2019年；坡度、沟谷密度数据是基于DEM数据在ArcGIS软件中提取得到；裸岩率数据是基于Landsat8影像提取得到，时间为2019年11月29日。

2.2 研究方法

(1) 逻辑回归方法。逻辑回归方法在解决地质灾害问题中，具有计算方法简单、能自动筛选影响因子等优点。可将对地质灾害发生产生影响的区划因子作为自变量，将地质灾害是否发生作为因变量(1代表发生，0代表未发生)[32]。考虑到各因子为非连续变量，本研究使用二元逻辑回归方法进行分析[33]，计算公式为：

(1)

式中：P为地质灾害发生的概率值； (1-P)为未发生地质灾害的概率值；X1，X2，…，Xn为区划因子；B1，B2，…，Bn为各区划因子对应的逻辑回归系数。

(2) 单因子信息量方法。由于各区划因子有不同标准的数据类型和数据量级，不能直接对其进行分析。所以，在使用逻辑回归方法之前需要将各区划因子进行异质数据同化。信息量法在本质上是一种数据驱动的定量统计方法，2001年信息量法被用于地质灾害易发性分级中。信息量法的主要思路为：根据历史灾害点，对各区划因子进行分级，将各区划因子的真实值转化为反映该研究区区划因子等级的信息量值，再根据信息量值来评判各区划因子与地质灾害的相关性。本研究即采用信息量法用于逻辑回归模型的异质数据同化。

对于单一评价因素的信息量i，计算公式为：

(2)

式中：S为研究区内评价单元的总面积；N为评价单元内发生地质灾害的总数量；Si为评价单元内特定类别的面积；Ni为分布在评价单元内特定类别的地质灾害的数量。

3 地质灾害易发性区划研究

3.1 地质灾害易发性区划因子选取

通过前期对林芝市公路沿线15 km缓冲区内的地形地貌、地质环境和生态环境的研究，发现其与地质灾害的分布紧密相关，同时，在中外地质灾害易发性区划模型的研究中，多数使用了坡度、断层、降水量等因子作为区划因子。因此，本研究最终选定8个区划因子作为地质灾害易发性区划模型的评价指标，包括断层密度、土地利用类型、土壤类型、坡度、沟谷密度、年均降水量、裸岩率和距河流的距离。再根据文献调研、实际经验和地质灾害点及隐患点分布规律对8个区划因子进行重分类(图2)。

3.1.1 地形地貌指标

(1) 坡度。坡度与气象水文条件、地表状况等因素紧密相关，是评价地质灾害的重要因素之一。一般情况下，坡度较大的地方会为地质灾害的发生提供大量物质来源。但坡度增大到一定限度后，发生地质灾害的概率将不会增大。本研究将坡度划分为0°～10°，10°～20°，20°～30°，30°～40°，>40°共5级。

(2) 沟谷密度。沟谷密度是气候、地形地貌、地层岩性、植被等因素综合影响的反映，沟谷密度与地面破碎程度成正比，地面越破碎，地表物质的稳定性越低，地质灾害的发生概率越高。本研究基于自然断点法将沟谷密度分为0～0.12，0.12～0.22，0.22～0.32，>0.32 km/km2共4级。

(3) 裸岩率。裸岩率是划分石漠化等级的重要参数，有些位居山地陡坡、土层较薄地带极易发展为裸露或裸岩地，从而引发地质灾害。本研究依据相等间隔法将裸岩率分为<0，0～0.2，0.2～0.4，0.4～0.6，0.6～0.8，0.8～1。

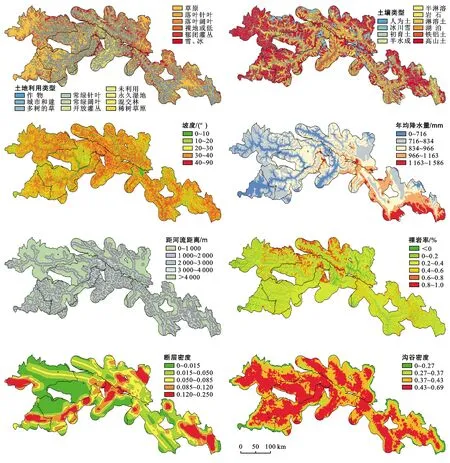
图2 林芝市公路沿线各区划因子分布

3.1.2 地质环境指标

(1) 断层密度。断层是影响地质灾害发生的重要因素之一，总体上距离断层越远，地质灾害点的分布密度越小，地质灾害的强发育区是在断层两侧的10 km范围内[34]。一般采用距断层的距离或断层密度来判断断层对地质灾害的影响程度。本研究选用断层密度作为评价指标，基于自然断点法将其分为0～0.015，0.015～0.05，0.05～0.085，0.085～0.12，>0.12 km/km2共5级。

(2) 距河流的距离。河流作为水文地质因素，其对地质岩层的影响十分显著，由此引发的地质灾害较为常见。水流反复流经会引起岩层塌陷，从而增加地质灾害的发生概率。本研究根据研究区实际情况，基于ArcGIS多环缓冲区工具将距河流的距离分为0～1 000，1 000～2 000，2 000～3 000，3 000～4 000，>4 000 m共5级。

3.1.3 生态环境指标

(1) 土地利用类型。土地利用类型可体现地表植被覆盖的状况和人类工程活动的强度。其中，植被覆盖状况与地质灾害发生密切相关，同时，人类工程活动(道路、房屋)也加剧了地质灾害的发生。本研究基于MOD12Q1土地利用产品数据的类型说明表进行分类。

(2) 土壤类型。不同土壤的特性会对地质灾害造成不同程度的影响，如土壤保水性能、渗水速率和含沙量等都会影响地质灾害的发生。本研究基于1∶100万中国土壤数据库中的土类进行分类。

(3) 年均降水量。降水条件对地质灾害的发生非常重要，降水下渗、洪水掏蚀河岸、水位变化等均会诱发地质灾害，根据前期对林芝市公路沿线降水特征分析，绝大多数地质灾害是由强降水诱发的。本研究基于自然断点法将年均降水量分为462～716，716～834，834～966，966～1 163，>1 163 mm共5级。

为了避免各区划因子数据类型和数据量级的不同而对结果产生影响，本研究基于单因子信息量方法对重分类后的8个指标进行异质数据同化，计算结果见表1。因子信息量值越大，表明地质灾害易发性概率越大。

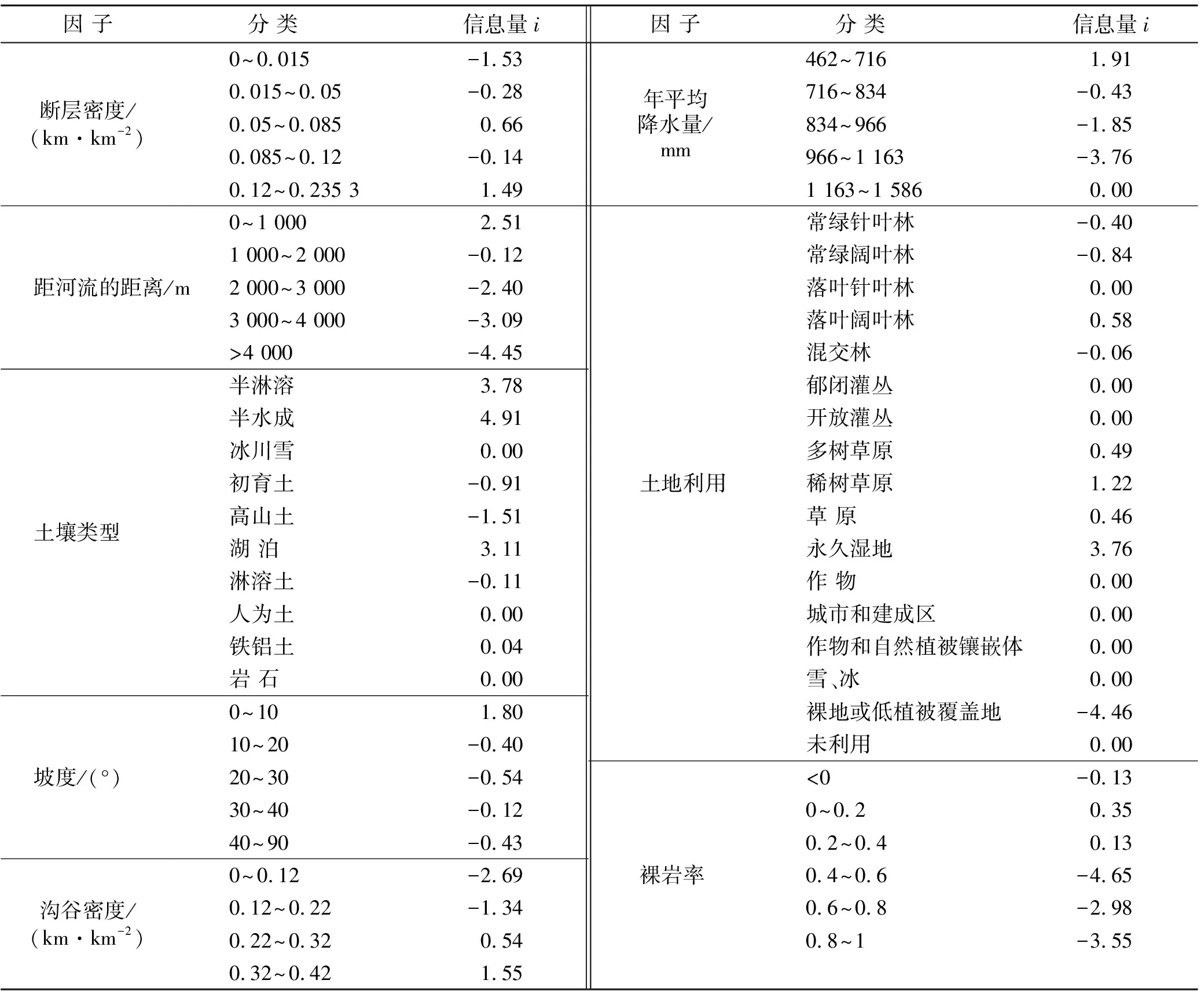
表1 单因子信息量计算结果

3.2 地质灾害易发性区划模型建立

本研究基于逻辑回归方法建立地质灾害易发性区划模型，以1 213个有效隐患点作为建模数据，152个有效灾害点作为模型验证数据(图1)。同时，为了使得二元逻辑回归分析更具有科学性，本研究基于张锡涛、常鸣等人[35-36]的研究，在以隐患点为中心的3 km缓冲区外随机选取对应数量的无灾害发生样本点。使用ArcGIS软件提取隐患点样本和无灾害发生样本的区划因子信息量值。将地质灾害是否发生作为因变量，断层密度、土地利用、土壤类型、坡度、沟谷密度、年降水量、裸岩率和距河流的距离信息量值作为自变量，在SPSS软件中构建二元逻辑回归模型。为了减少无灾害发生样本数据对模型产生的影响，多次进行无灾害发生样本的选取并循环建模，最优结果的Nagelkerke方差可达到0.769，Cox & SnellR方差可达到0.577。表2为区划因子逻辑回归结果，其中，B为系数，S.E为标准差，Wald统计量越大表示该因子的重要性越强，从表2可以看出，各区划因子重要性依次为：河流、坡度、土壤类型、断层密度、年降水量、土地利用、沟谷密度、裸岩率，8个区划因子的显著性均小于0.05，显著性较高，具有统计学意义。

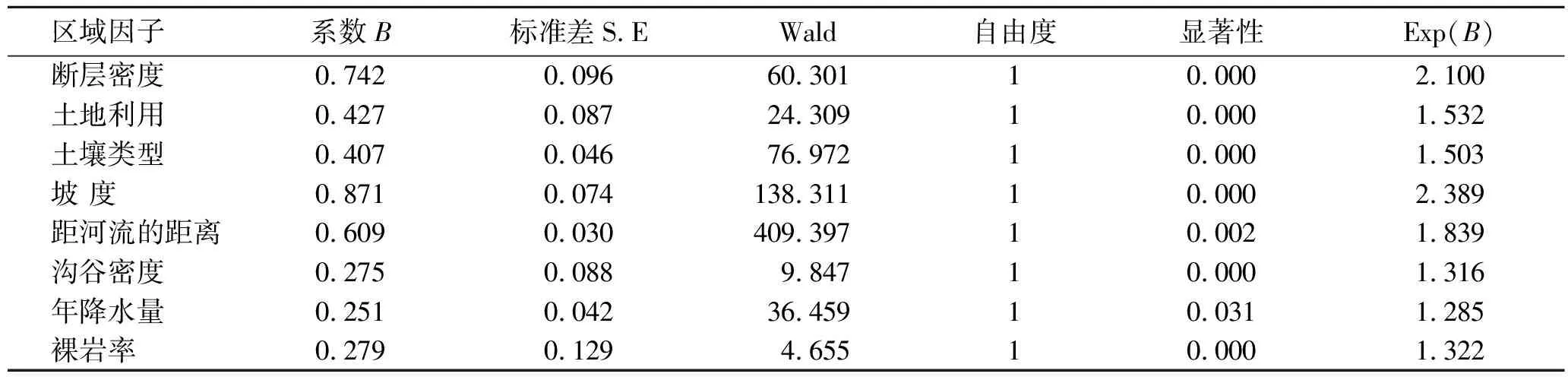
表2 研究区区划因子逻辑回归方程

将表2中各因子系数代入公式中计算地质灾害易发性概率值，计算公式为：

(3)

式中：H为地质灾害易发性概率值；X1—X8分别为断层密度、土壤类型、坡度、沟谷密度、年降水量、土地利用、裸岩率、距河流的距离信息量值。

将8个区划因子的信息量值和系数代入公式(3)计算出地质灾害易发性概率值，用ArcGIS软件进行加权叠加分析得出林芝市公路地质灾害易发性概率值，然后进行易发性分区，形成分区图(图3)。以0.1为间隔，将林芝市公路地质灾害易发性概率分为10级。从图3可知，林芝市公路地质灾害易发性概率超过0.8的主体区域主要分布在朗县中部、林芝县东部、墨脱县境内扎墨公路、察隅县东部的察佐公路及察丙路附近；工布江县、波密县大部分区域易发性概率小于0.4，不易发生灾害。总体趋势是离道路越近，易发性概率越大。

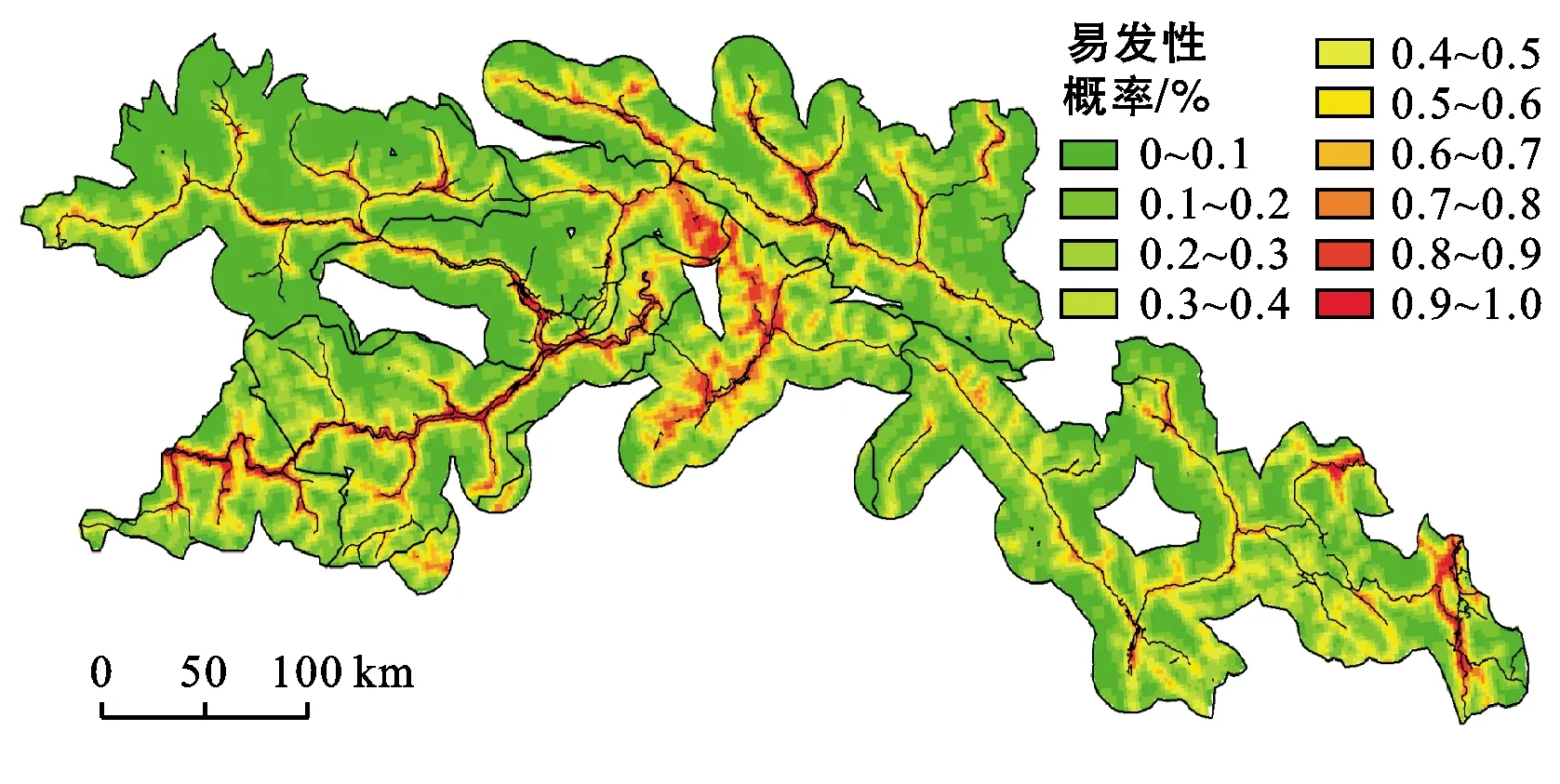
图3 林芝市公路沿线地质灾害易发性区划

4 地质灾害气象预报模型研究

4.1 地质灾害与降水诱发灾害概率关系研究

本研究基于前期整理的2010—2019年地质灾害资料和降水资料，将地质灾害是否发生作为因变量，日降水量作为自变量，以逻辑回归方法作为耦合手段分析地质灾害与降水诱发灾害概率关系。林芝市截止至2019年约有66个气象站点的日降水数据，由于2010—2019年增加或弃用的气象站点较多，则利用ArcGIS邻域分析工具，分别提取2010—2019年距历史灾害点最近雨量站的日降水量平均值作为灾害点的降水量。相比于降水量空间插值的方式，此方法保证了灾害发生当日及前期降水量的准确性。样本点选择方式是选择历史地质灾害点中有准确降水量的样本点152个，并加入同等数量的无灾害发生样本点，其中，无灾害发生样本点的日期选择方式是选取2010—2019年汛期(5—9月)较长时间无灾害发生的日期，并随机分配给无灾害发生样本点。

基于灾害点样本、无灾害发生样本和前6日的日降水数据，构建逻辑回归模型。拟合发现，前4日、前5日和前6日降水量未通过显著性检验。剔除后重新建模，最优结果的Nagelkerke方差可达到0.516，Cox & Snell R方差可达到0.387，各建模因子均通过显著性检验(表3)。

降水诱发地质灾害概率的公式为：

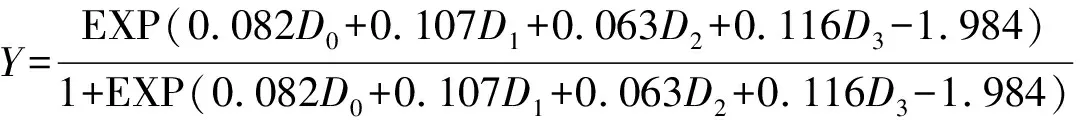
(4)

式中：Y为降水诱发地质灾害概率值；D0，D1，D2，D3分别为灾害发生当日、前1日、前2日、前3日降水量。

表3 研究区建模因子逻辑回归方程

4.2 地质灾害气象预报模型建立

根据刘传正等人对国内外地质灾害气象预报模型原理的总结[37]，本研究选取显式统计预报模型的方法，基于逻辑回归方法，对地质灾害易发性概率H值与降水诱发地质灾害概率Y值进行分析，最终得到研究区内地质灾害发生的概率值[38]，其计算公式为：

T=a·H+b·Y

(5)

式中：T为地质灾害发生概率值；H为地质灾害易发性概率值，是地质要素对地质灾害发生的综合体现；Y为降水诱发地质灾害概率值；a为易发性区划占地质灾害发生概率权重系数；b为降水因素占地质灾害发生概率权重系数。

经拟合，T模型逻辑回归结果的Nagelkerke方差可达到0.681，Cox & SnellR方差可达到0.51，模型拟合度较高，通过了显著性检验，获得最终的系数详见表4。由于模型最终结果是概率值，因此，本研究将表4中的系数归一化至0～1之内，系数四舍五入后得到a=0.373，b=0.627。

表4 研究区T模型逻辑回归方程

4.3 地质灾害气象预报模型检验

为了确保模型的可操作性，本研究选取部分历史地质灾害点对模型进行精度验证，将日降水量数据和地质灾害易发性概率H值放入地质灾害气象预报T模型中，计算出地质灾害发生概率T值。再结合统计分析及专家经验，确定T值超过0.4发布黄色预警，超过0.6发布橙色预警，超过0.8发布红色预警。

4.3.1 模型预测准确率计算 选取49个未参与建模的灾害点数据作为模型的检验数据。将49个灾害点对应的当日、前1日、前2日和前3日降水量数据和地质灾害易发性概率H值放入地质灾害气象预报T模型中计算，得到不同预报等级的灾害点个数，预报结果详见表5。从表5来看，预报区85.71%的灾害点达到黄色预报级别，14.29%的灾害点达到橙色预报级别，14.29%的灾害点达到红色预报级别。所以，该模型的预报准确率为85.71%，模型的漏报率为14.29%。

表5 研究区地质灾害模型预报效果等级分布

4.3.2 模型个例检验 本研究以2020年7月11日318国道林芝县至波密县路段多处发生的地质灾害为例，验证地质灾害气象预报模型的应用效果。7月8—11日连续4日318国道林芝县至波密县路段有强降水，7月8—11日降水量最大值分别为23.0，35.6，77.3和78.5 mm，将这4日降水量数据带入地质灾害气象预报模型计算得到2020年7月11日地质灾害预报结果(图4)。据统计，2020年7月11日318国道林芝县至波密县路段发生的地质灾害点有3个，均达到了橙色预报级别，其中，达到了红色预报级别的灾害点有2个。至此，本研究认为该模型的预报准确性较高，可以为林芝市境内公路沿线地质灾害气象预报提供一定的依据。

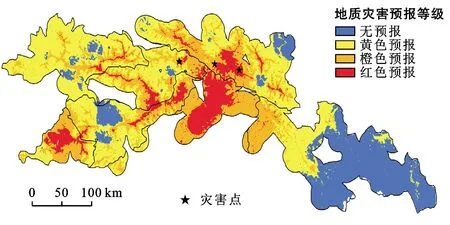
图4 研究区2020年7月11日地质灾害预报结果

5 结 论

(1) 针对林芝市公路沿线的地质特性，选取了断层密度、土地利用、土壤类型、坡度、沟谷密度、年降水量、裸岩率和距河流的距离8个地质灾害易发性区划因子，并通过信息量及逻辑回归方法确定各区划因子的系数，系数分别为0.742，0.407，0.871，0.275，0.251，0.427，0.279，0.609。根据林芝市公路地质灾害易发性区划结果图可以看出，地质灾害易发性概率超过0.8的主体区域主要分布在墨脱县境内扎墨公路、察隅县东部的察佐公路及察丙路附近；大部分区域易发性概率小于0.4，总体趋势是离道路越近，易发性概率越大。

(2) 基于地质灾害易发性概率值和灾害发生当日、前1日、前2日和前3日的日降水数据，通过逻辑回归方法构建了林芝市公路地质灾害气象预报模型。通过对模型进行检验发现，模型预报准确率为85.71%，漏报率为14.29%。

(3) 受林芝市公路沿线地形地貌影响，气象站点分布不均匀，高海拔地区站点少，地质灾害发生地的实际降水与降水资料有偏差。同时，历史地质灾害点信息监测及采集困难，存在错报及漏报情况。所以，本研究的预报结果可能与实际情况有一定的偏差，但能反映基本趋势。在未来的研究中，研究人员可通过灾害数据筛选、气象预报模型优化等方式降低模型漏报率，保证实际运行时的预报准确度。