高超声速钝前缘乘波构型优化设计研究1)

郭帅旗 *, 刘 文 *, 张陈安 * 王发民 *

* (中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190)

† (中国科学院大学工程科学学院,北京 100049)

引言

对于近空间远程机动高超声速飞行器来说,升阻比决定着其航程和横向机动距离.然而,传统构型在高超声速条件下会面临“升阻比屏障”[1].目前,乘波体是最有潜力打破这一屏障的布局之一.乘波体的设计原理由Nonweiler[2]提出,其以绕楔形体的流场为基准流场,在流场激波面上任意定义一条曲线作为前缘线,从前缘出发的所有流线构成的流面作为乘波体下表面,以自由来流平面作为上表面,生成了最初的“Λ”型乘波体.在设计工况下,激波附着于乘波体的整个尖前缘上,从而将高压气体限制在激波和下表面之间,避免了下表面的流动上溢,这一特征使得乘波体在高超声速条件下具备极高的气动效率.Moore 等[3-4]使用圆锥形流场作为基准流场,从前缘线出发进行流线追踪生成了锥导乘波体,由于圆锥激波后流线更接近激波,因而锥导乘波体比“Λ”型乘波体的容积更大,更接近工程应用.Takashima和Lewis[5]提出了在楔-锥组合非轴对称三维流场中生成乘波体的方法.Sobieczky 等[6]提出了密切锥乘波体设计方法,该方法可以通过给定任意形状的激波来生成乘波体,使得生成的乘波体外形更加灵活.Rodi[7]进一步将此类方法扩展到密切流场法.文献[8-10]发展了密切内锥和密切曲面锥的乘波体设计方法,使得乘波体具有更好的容积特性和流动压缩能力.Zheng 等[11]提出了局部偏转密切乘波设计理论,进一步拓展了密切乘波体设计空间.刘传振等[12]基于定后掠乘波体研究,提出了双后掠乘波体的概念,为宽速域高超声速飞行器设计提供了新思路.此外,近年来国内外学者又相继提出了多种乘波体设计方法[13-20].文献[21-22]对国内外各类乘波体的发展方法进行了详细总结.

在实际工程应用中,为了满足防热要求,需要对乘波体前缘进行钝化处理.Gillum 和Lewis[23]关于钝化乘波体的实验结果表明,钝化会造成阻力增加,升阻比降低.陈小庆等[24]通过CFD 方法研究了不同钝化半径对乘波体气动力、热的影响,结果表明,前缘钝化会显著降低乘波体气动力性能,同时改善气动热,并且钝化半径越大,气动力性能降低越明显.Liu等[25]通过数值模拟和实验对钝化乘波体进行了研究,结果表明,随着钝化半径增加,乘波体气动力性能显著降低,而高热流主要集中分布在靠近头部驻点附近的前缘区域.从上述研究可知,前缘钝化会显著降低乘波体的气动力性能.

目前在乘波体优化过程中,都是针对原始尖前缘构型进行优化.例如,Bowcutt 等[26]在锥导乘波体设计过程中考虑黏性影响得到黏性优化乘波体,李维东等[27]进一步在乘波体优化过程中考虑了强黏性干扰效应影响.根据已有文献分析可知,前缘钝化对乘波体气动特性会产生显著影响.此外,由于不同乘波体前缘线分布特征不同,前缘钝化对不同构型的影响也必然存在差异.可以推断,原始尖前缘最优乘波体并不能保证钝化后仍为最优构型.因此,开展直接考虑前缘钝化效应影响的乘波体优化研究是很有必要的.

针对上述问题,本文首先以三个典型乘波体为例,研究了前缘钝化对不同乘波体升阻特性的影响程度和影响机理;在此基础上,提出了一种高效评估钝前缘乘波体气动力的方法,并结合遗传算法,开展直接考虑前缘钝化影响的乘波构型优化设计研究,获得了具备更高升阻比的钝前缘乘波构型.

1 乘波体生成和数值模拟方法

1.1 乘波体生成方法

本文以锥导乘波体为研究对象,在锥形流场确定后,乘波体外形由前缘线形状决定.一般先在底面上定义一条样条线,再将其沿来流方向投影至激波面,所获得的交线即为乘波体的前缘线,如图1 所示,图中X轴从尾部指向头部,Y轴在水平面上指向右侧,Z轴根据右手定则确定,即在铅垂平面指向下方.此处采用如下形式的三次多项式定义基准平面上的基准曲线

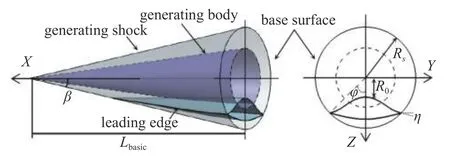
图1 锥导乘波体生成过程Fig.1 Generation of cone-derived waverider

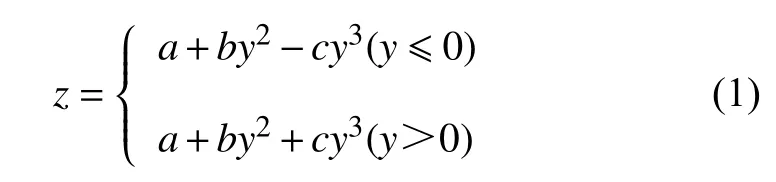
为了更清晰直观地描述该曲线,设激波圆半径为Rs,基准曲线Z截距为R0,方位角为φ,令曲线与激波圆交点位置处的切线与Y轴的夹角为η,并令参数kw=R0/Rs.参数kw,φ和η确定后,可得到式(1)的系数

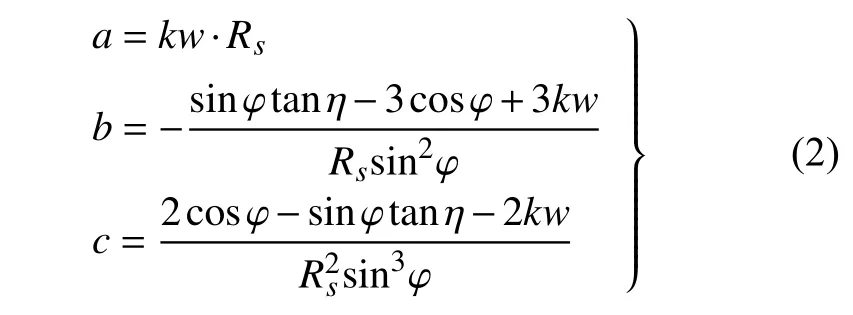
令基准圆锥的长度Lbasic=1,由激波角即可求得Rs,再给定设计参数kw,φ和η的值,即可完全确定基准曲线,进而确定乘波体前缘线.之后,从前缘出发在激波后流场进行流线追踪即可生成下表面,上表面沿自由来流生成.获得乘波体上、下表面之后,将其等比例放缩至所需长度即可确定最终的乘波体构型.

本文以如图2 所示三个典型乘波体为例,研究钝化对乘波体气动性能的影响,其设计工况均为:来流马赫数M∞=15,激波角β=8.5°,长度L=4 m,设计参数kw=0.4,η=20°,从左至右φ分别为40°,50°,60°.从图2 可以看到,从左至右乘波体宽度逐渐增加.

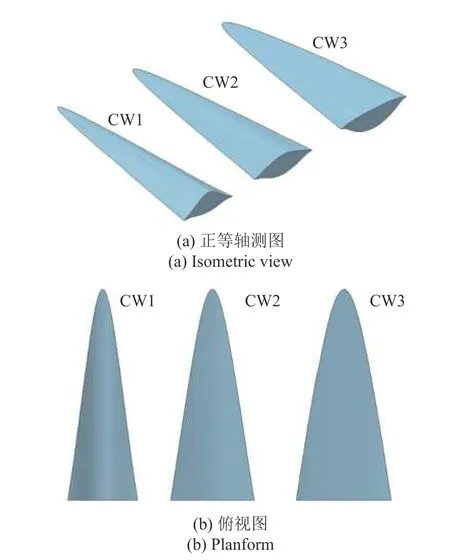
图2 典型乘波体对比Fig.2 Comparison of typical waveriders

为了保持乘波体前缘线和升力面形状不变,本文采用Tincher 和Burnett[28]建议的“加材料”方法对乘波体进行前缘钝化,如图3 所示.

图3 乘波体前缘钝化示意图Fig.3 The waverider with blunted leading edge

1.2 数值模拟方法

本文通过CFD 来评估钝化前后乘波体的气动特性.采用格心格式有限体积法求解N-S 方程,空间离散采用AUSM+格式,时间离散采用隐式LUSGS 方法.上述数值模拟方法在强黏性干扰飞行条件下的精度验证见文献[29-30],其中数值计算得到的航天飞机OV-102 的轴向力系数和升阻比与ADDB 手册给出的结果十分接近,证明了该数值模拟方法的可靠性.由于本文研究的高空高马赫数飞行条件(M∞=15,飞行高度H≥ 40 km)和较小的乘波体长度(L=4 m),雷诺数较低,因此在计算摩阻时,都采用层流模型.

1.3 网格无关性验证

由于外形的对称性,此处采用半模计算网格对钝前缘乘波体进行数值模拟,如图4 所示.采用三种不同数量网格进行网格无关性验证,网格数量分别约为307 万(coarse)、611 万(medium)和1364 万(fine),第一层网格的高度为1 × 10-4m.在计算工况:M∞=15,H=50 km,α=0°,不同网格气动力对比如表1 所示.可以看到,不同网格结果差异很小,medium 和fine 的各项气动力结果相差均不超过1%,满足网格无关性要求.为了提高计算效率,本文采用medium 网格来进行CFD 计算.

图4 半模计算网格(约611 万)Fig.4 Half-model grid used in numerical simulations (approximately 6 110 000 cells)

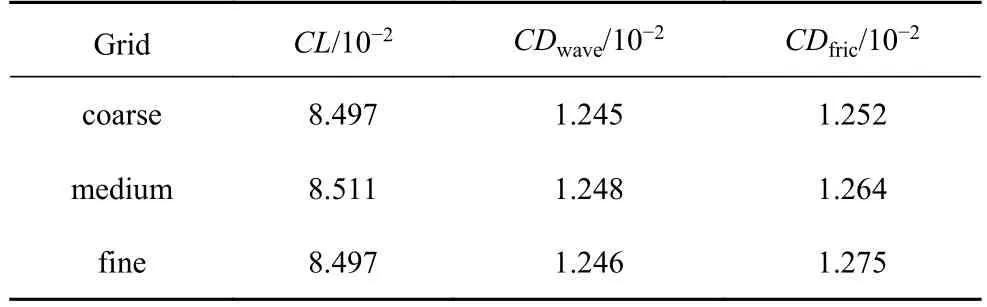
表1 不同网格气动力对比Table 1 Comparison of force coefficients at the condition:M∞=15,H=50 km,α=0°

2 钝化影响

2.1 不同钝化半径对升阻比的影响

以CW1 乘波体为例,研究不同钝化半径对气动性能的影响,钝化半径依次为10 mm,15 mm,20 mm.钝化前后乘波体升阻比随攻角变化的对比如图5 所示.从图中可知,钝化后乘波体升阻比显著降低,且钝化半径越大,升阻比越低.图6 和图7 分别对比了钝化前后的升力、阻力及其增量相对原始尖前缘乘波体升力、阻力的比值.从图中可知,钝化造成升力小幅度降低、阻力显著增加,并且钝化半径越大,阻力增量越大.当钝化半径R=20 mm 时,升力最大降低6.41%,阻力最大增加24.05%.因此,钝化后阻力的增加在升阻比降低中起主要作用.

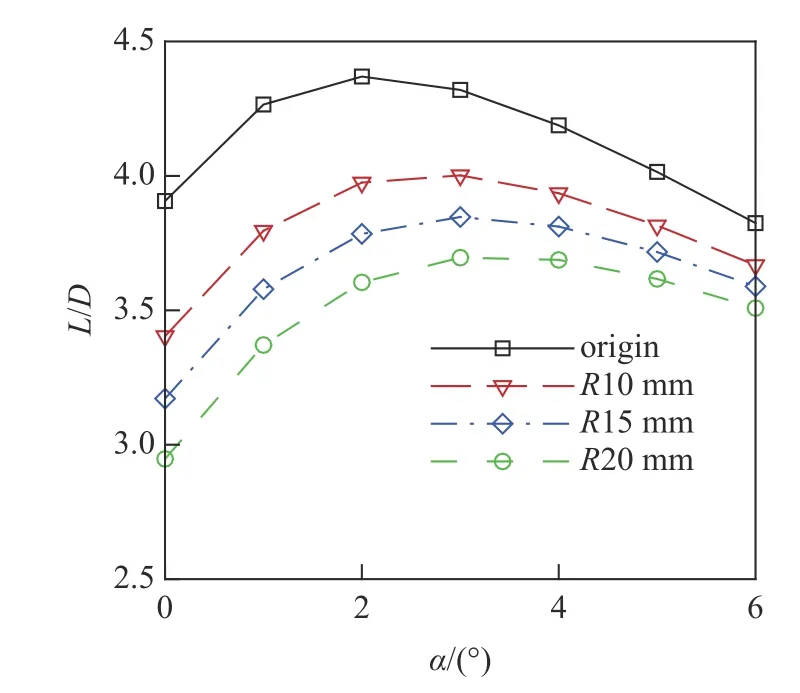
图5 钝化前后升阻比对比Fig.5 The L/D at the different blunt radii

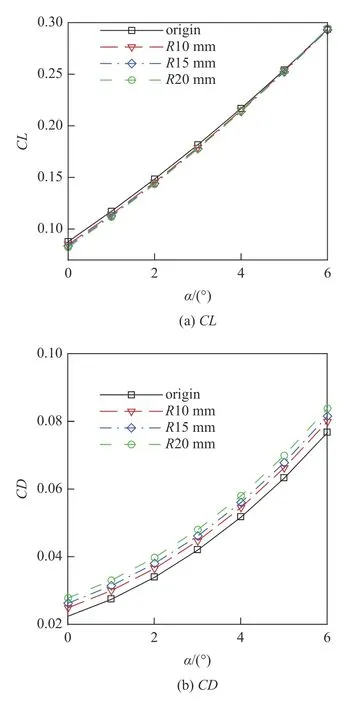
图6 钝化前后乘波体升阻特性对比Fig.6 The lift and drag coefficient at different blunt radii

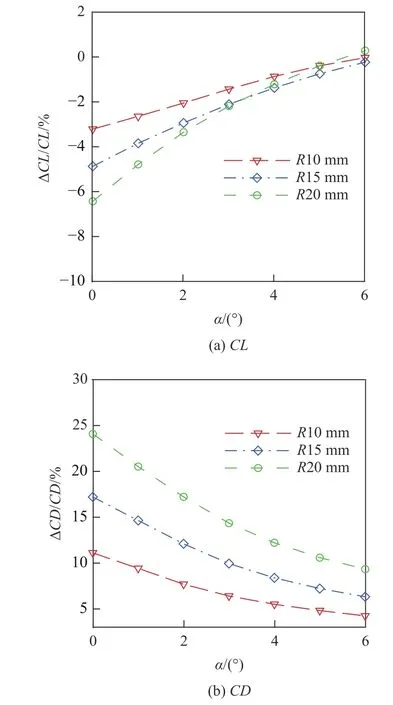
图7 钝化前后升力、阻力系数相对增量对比Fig.7 The lift and drag coefficient increment at different blunt radii

2.2 前缘钝化对升阻比的影响

乘波体钝化对升阻特性的影响主要分为两部分:(1)钝前缘本身的升力及阻力;(2)钝前缘产生的脱体激波对上、下表面升阻特性的影响.以钝化半径R=10 mm 的CW1 为例,研究前缘钝化对乘波体升阻特性的影响.

图8 给出了CW1 钝化后各部分升力增量占原始尖前缘乘波体总升力比值的对比,其中total_R10 mm 表示总升力、leading-edge 表示钝前缘本身、upper+lower 表示上下表面.从图中可知,钝前缘本身带来的升力增量最大为1.96%,脱体激波造成的上下表面升力降低量最大为5.16%,在二者共同作用下,造成总升力最大降低3.20% (α=0°).

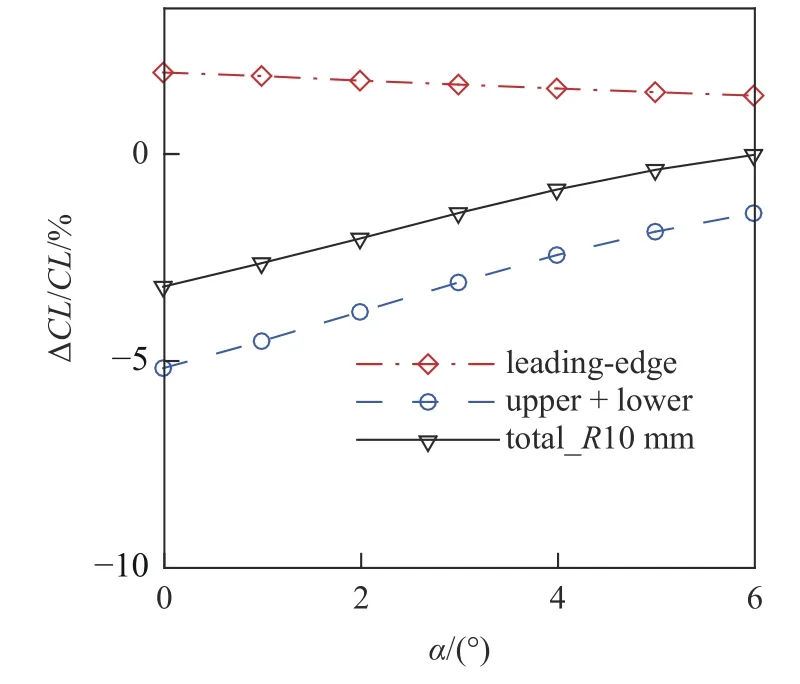
图8 钝化前后乘波体升力增量对比Fig.8 Comparison of the lift coefficient increment

图9(a)对比了CW1 钝化后各部分波阻增量占原始尖前缘乘波体总阻力的比值.从图中可知,钝前缘带来的波阻增量最大为11.41%,前缘钝化造成上下表面波阻降低,最大为2.01%.钝前缘本身的波阻在总波阻增量中起主导作用,使得总波阻最大增加9.40% (α=0°).图9(b)对比了CW1 钝化后各部分摩阻增量相对原始尖前缘乘波体总阻力的比值.可以看出,钝前缘带来的摩阻增量最大为12.56%,前缘钝化导致上下表面摩阻降低,最大为10.87%.在二者共同影响下,总摩阻增加,但最大增量仅为1.69%(α=0°).

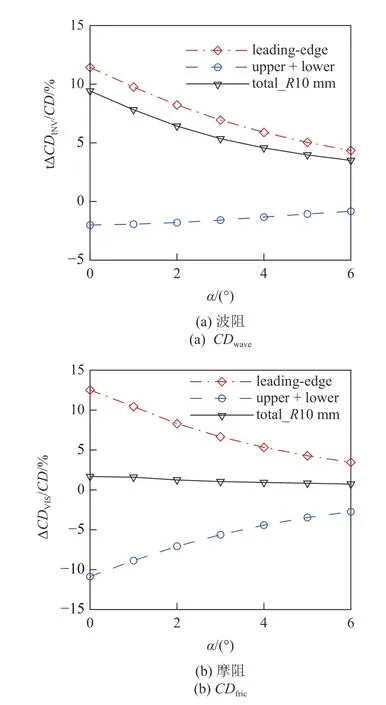
图9 钝化前后乘波体阻力相对增量对比Fig.9 Comparison of the drag coefficient increment of different parts

根据上述分析可知,钝化后钝前缘本身的波阻增量在总阻力增量中起主导作用.

2.3 脱体激波对物面影响的机理

仍以钝化半径R=10 mm 的CW1 乘波体为例,分析脱体激波对上下表面升阻特性的影响机理.图10(a)对比了零攻角时钝化前后乘波体中心线压力分布.可以看到,钝化后下表面靠近头部的压力明显高于钝化之前,然而,头部下游压力会逐渐降低到低于尖前缘压力,之后,压力又逐渐恢复到与尖前缘压力相当的水平,这种现象被称为“压力过膨胀效应”[31].原因从图10(b)可以看出:钝前缘产生的膨胀波一部分与声速线相交,一部分与脱体激波相交.与声速线相交的膨胀波被反射为压缩波,与脱体激波相交的膨胀波被反射为膨胀波.在钝前缘产生的膨胀波与反射出的压缩波、膨胀波的作用下,造成压力会先降低到低于钝化前的压力,之后又逐渐恢复到与钝化前压力相当的水平.图10(c)对比了不同攻角下钝化前后下表面中心线压力分布.可以看到,攻角越大,下表面的压力过膨胀效应越显著,且钝化后压力最小值的位置越靠前.

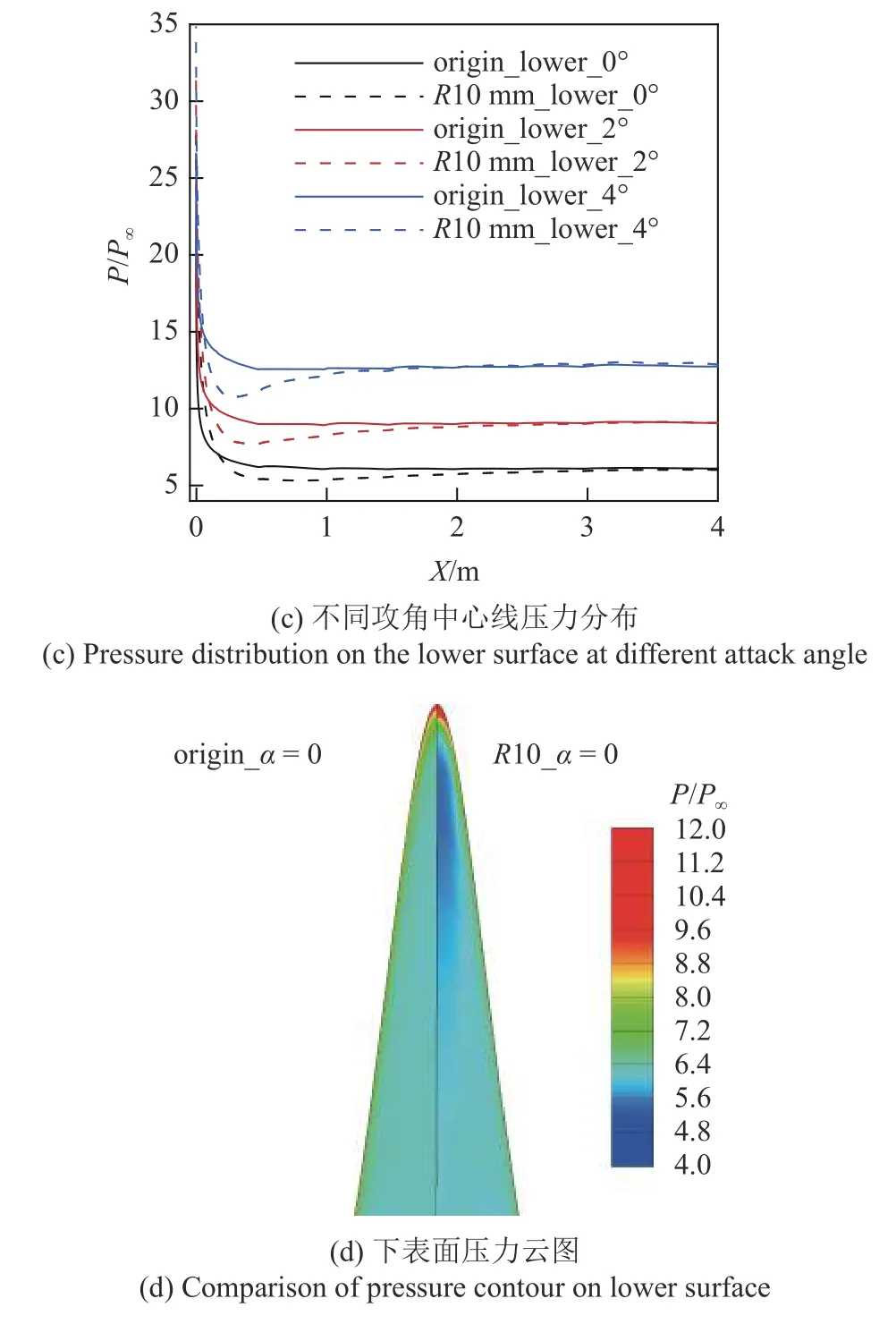
图10 钝化前后压力分布对比Fig.10 Comparison of pressure distribution

根据上述分析可知,钝化后靠近头部区域物面压力显著增大,下表面对称面附近大部分区域压力会小幅降低,如图10(d)所示,图中左右两侧分别对应原始尖前缘乘波体和钝化乘波体.压力分布的改变导致下表面升力和波阻均降低,但由于压力降低幅度较小,钝化造成的物面升力和波阻降低量均较小.

图11 和图12 分别对比了钝化前后不同截面处物面附近无量纲速度云图和对称面速度型.从图中可知,钝化后边界层厚度显著增加,导致边界层内速度梯度显著降低,从而使得上、下表面的摩阻明显降低,如图9(b)所示.

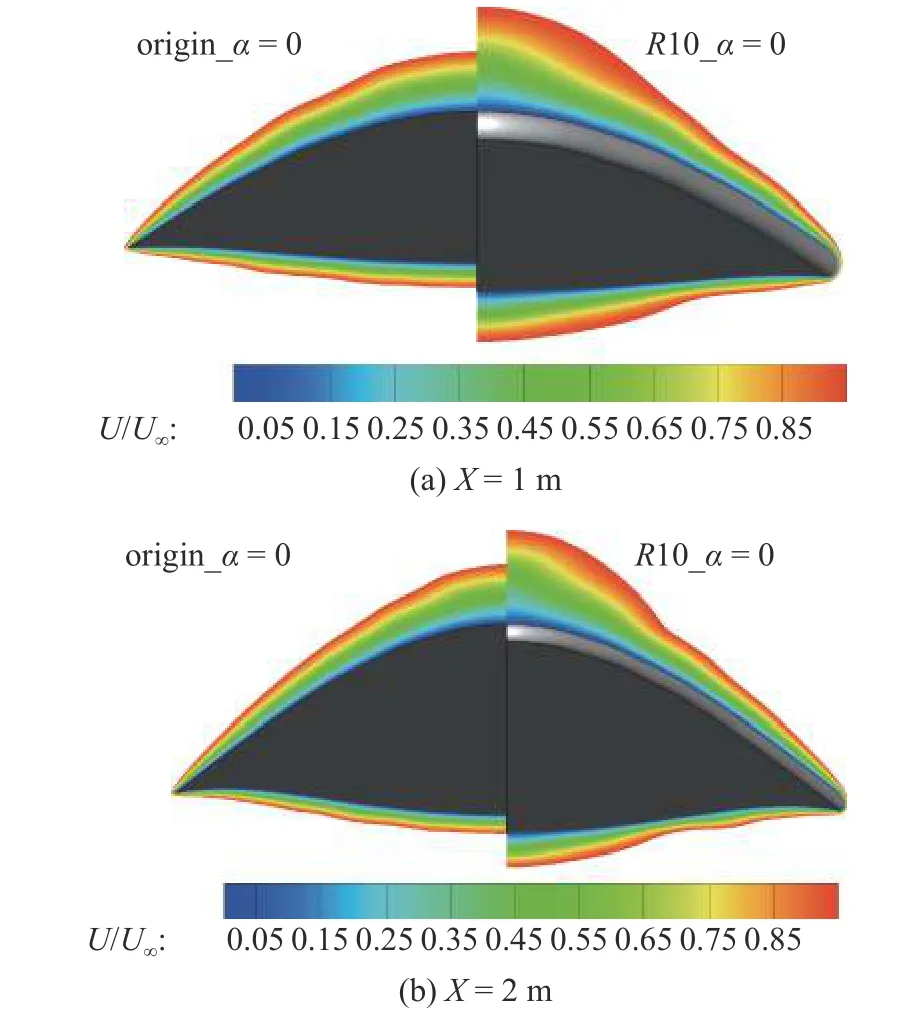
图11 钝化前后无量纲速度云图Fig.11 Comparison of velocity contour

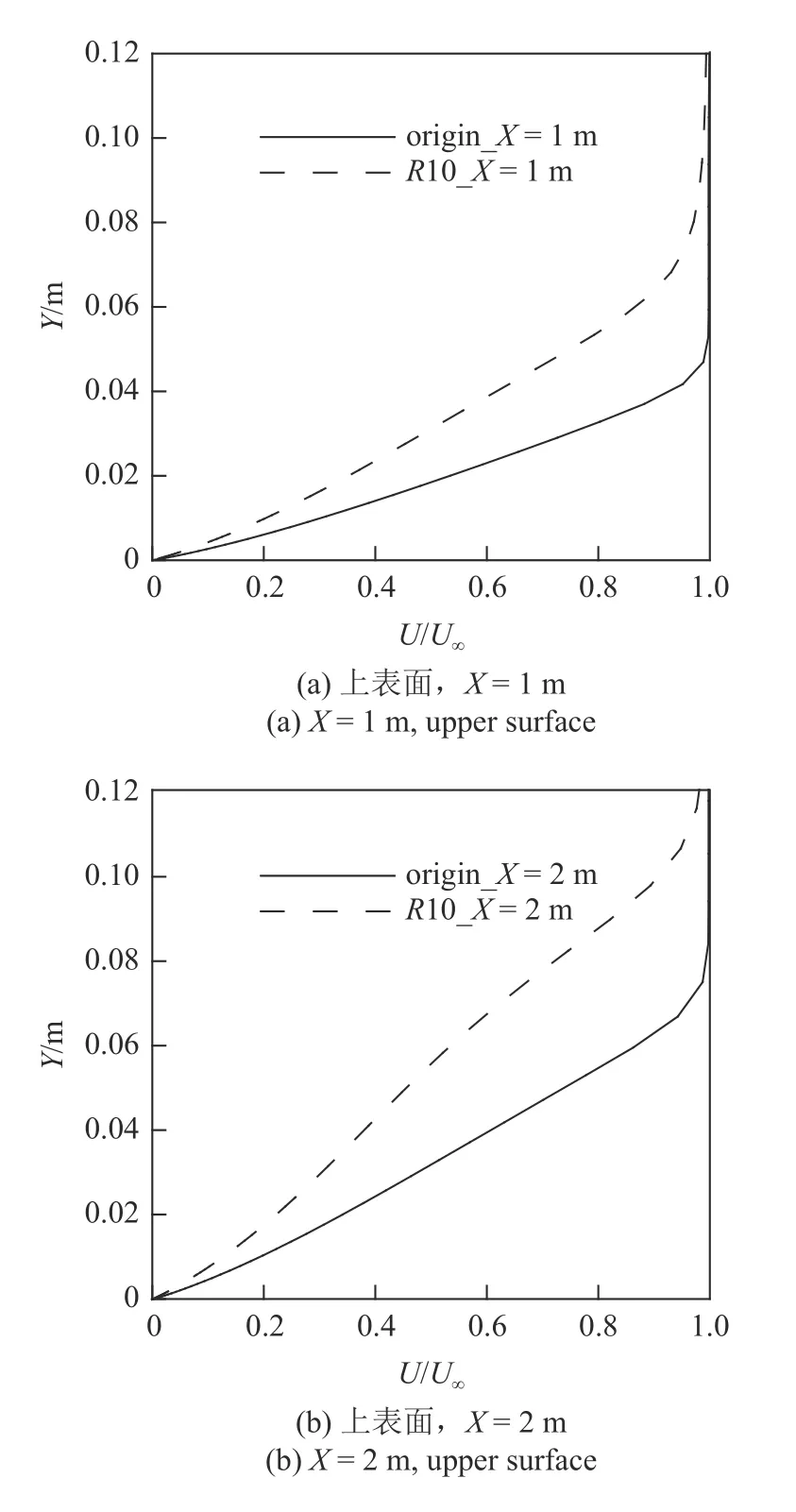
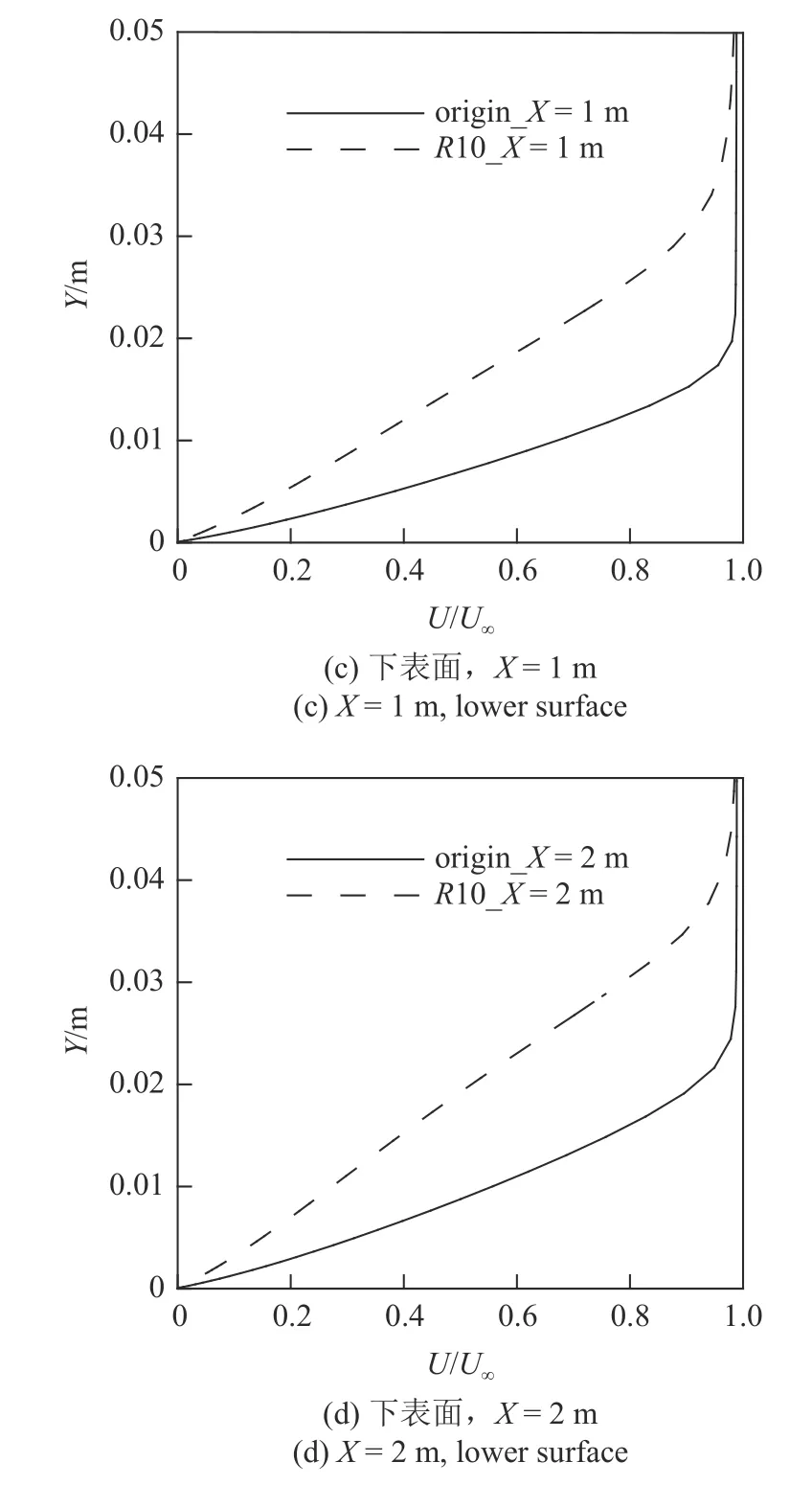
图12 上下表面中心线不同位置速度型对比Fig.12 Comparison of velocity profiles of symmetry plane

根据上述分析可知,脱体激波对物面升阻特性的主要影响是显著降低摩阻.由于传统的高超声速气动力模型捕捉不到前缘钝化造成的“压力过膨胀效应”,因此难以准确获得钝化后乘波体上下表面的压力分布;而传统的高超声速摩阻公式(式(11))需要已知当地压力,显然其难以有效评估脱体激波造成的摩阻降低效应.然而,上述前缘钝化对升阻特性影响的分析结果为钝前缘乘波体气动力评估提出了一个新思路.由于钝化后乘波体总摩阻变化较小,因此可认为钝前缘本身的摩阻增加量和上下表面的摩阻降低量相互抵消,即可忽略钝化对乘波体总摩阻的影响.其次,相比于钝前缘本身的波阻增量,上下表面的波阻降低量较小,同样可以忽略上下表面的波阻变化.此外,由于前缘钝化造成的乘波体升力变化量较小,可忽略其影响.

因此,对于本文所研究的锥导乘波体以及所关注的飞行工况,只需要在原始尖前缘乘波体气动力的基础上增加钝前缘本身的波阻影响即可以有效的评估钝化乘波体的气动力.

为了进一步验证上述假设的合理性,图13～图15 给出了不同钝化半径、不同工况和不同外形的阻力增量占原始尖前缘总阻力比值的对比,其中“total”表示总阻力,“INV”表示总波阻,“VIS”表示总摩阻,LE-INV 表示钝前缘本身波阻.从图中可知,不同条件下钝化后总的摩阻增量都较小(最大不超过3%),且总阻力增量和钝前缘本身波阻之间相差均较小.

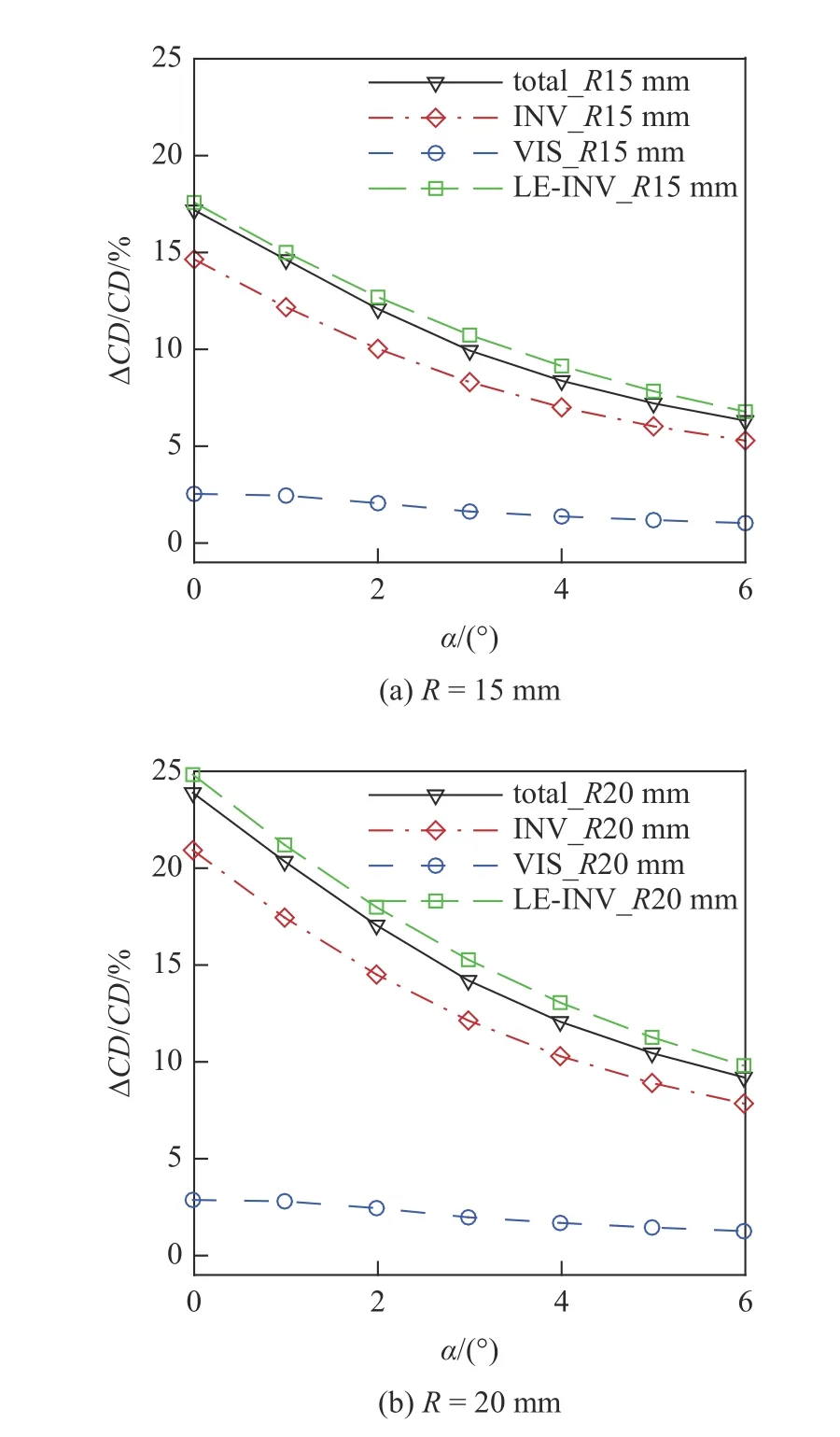
图13 不同钝化半径下阻力分量变化量对比Fig.13 The drag coefficient of the waverider with different blunt radii

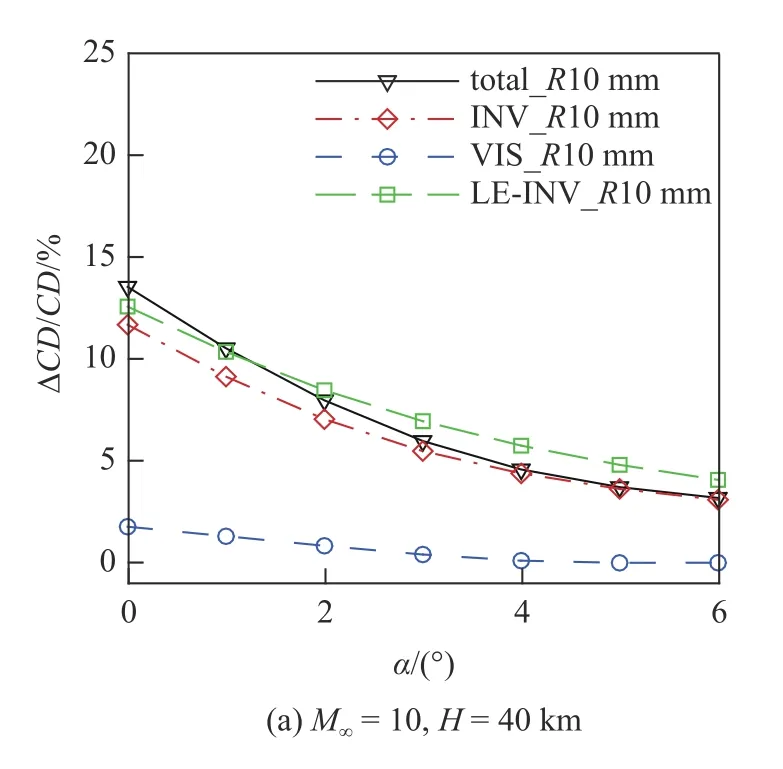
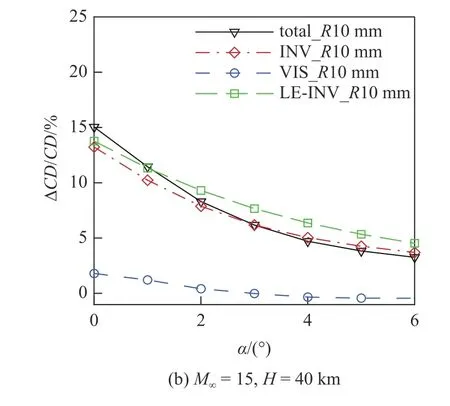
图14 不同工况下阻力分量变化量对比Fig.14 The drag coefficient at different flight conditions

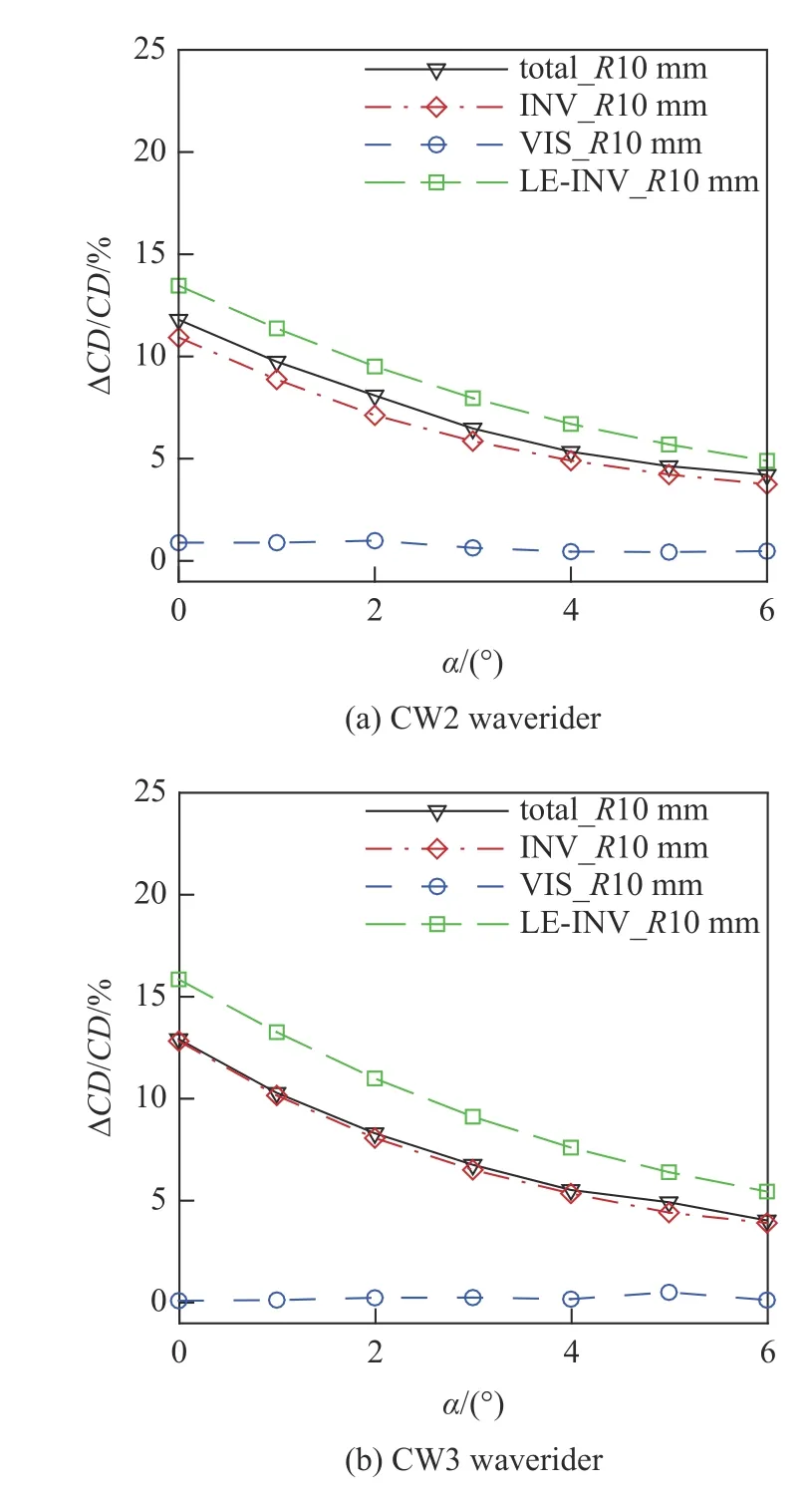
图15 不同乘波体构型阻力分量变化量对比Fig.15 The drag coefficient of different waveriders

3 研究方法

基于上述分析结果,本文提出一种评估钝前缘乘波体气动力的近似方法,即以钝前缘本身的波阻增量作为钝化造成的总阻力变化量,并忽略钝化对乘波体升力的影响.利用该气动力评估方法,在乘波体优化设计过程中直接考虑钝化影响,可优化得到钝前缘最优乘波体.

3.1 气动力工程算法

在飞行器初始优化设计阶段需要对气动特性进行快速准确的评估.CFD 技术巨大的计算量使得其难以满足飞行器初始设计过程中的快速迭代需求,在优化过程中需要借助高效的工程模型来快速计算气动力.优化结果的可靠性很大程度上取决于气动力模型的精度.因此,参照文献[32],本文采用一种改进的切锥法来快速预测迎风面压力分布[33];对于膨胀区域,采用膨胀波关系式计算[34],具体表达式为

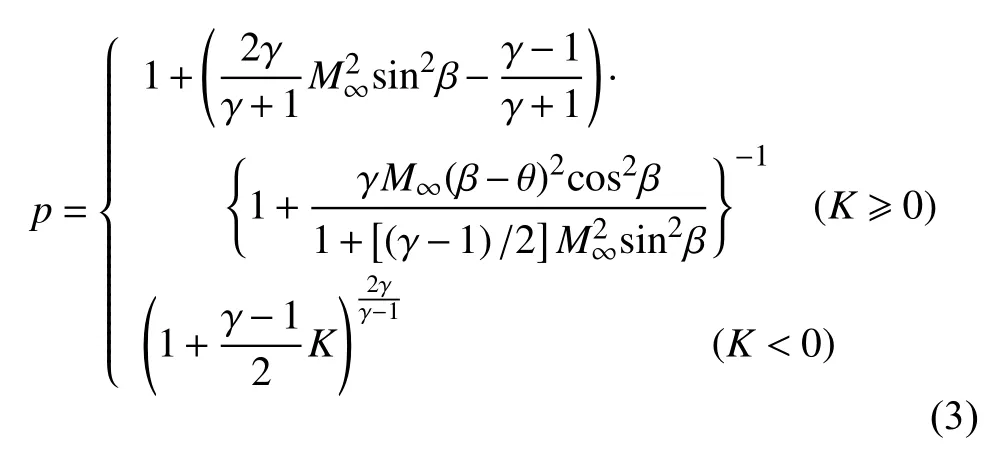
其中p=pw/p∞,高超声速相似参数K=M∞θ,θ为物面与来流方向夹角,比热比γ=1.4.对于给定的来流马赫数M∞和物面倾角θ,激波角β可由下式确定[34]

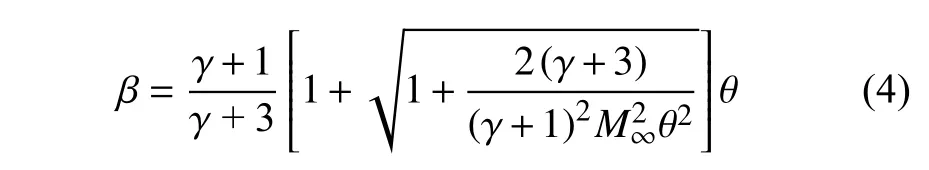
本文采用Bertram[34]提出的半经验方法来快速计算物面边界层位移厚度,具体表达式为

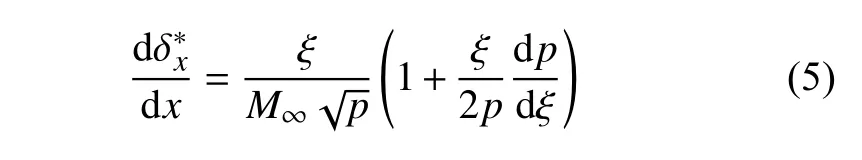
式中

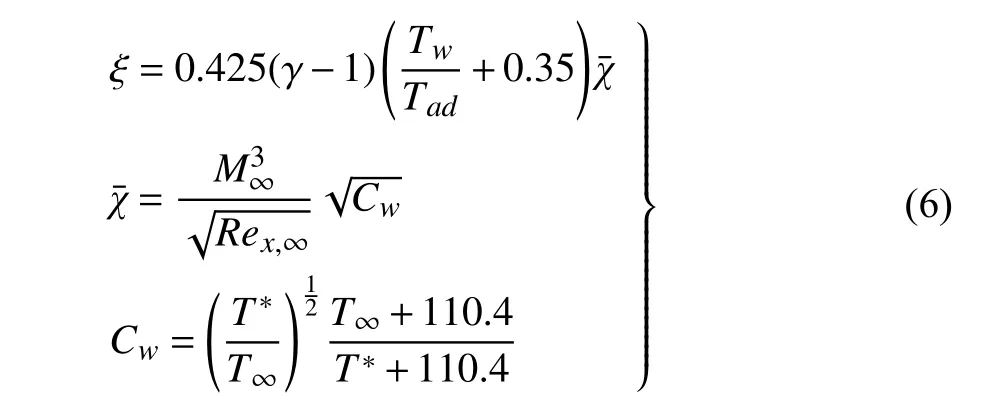
下标为∞和w的量分别表示来流和物面处的物理量;Tad表示绝热壁温,T*为参考温度.

本文采用的参考温度计算公式为[35]

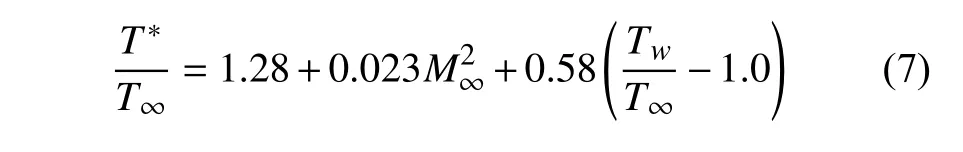
绝热壁温计算公式为

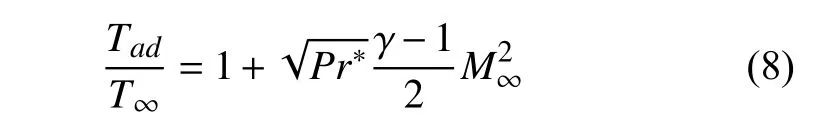
其中Pr*=0.72,本文采用的壁面温度Tw=1000 K.

钝前缘本身的压力采用修正的牛顿理论[36]进行计算,具体表达式为

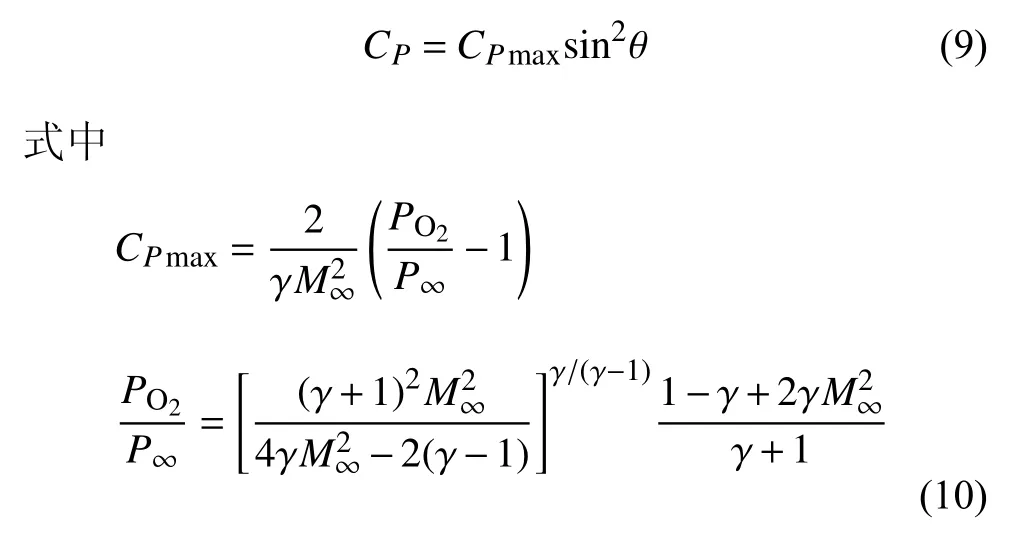
具体的气动力计算步骤如下:

(1)根据式(3)计算原物面压力分布;

(2)根据式(6)～ 式(8)计算物面边界层中的黏性干扰参数和ξ;

(3)联立式(3)和式(5)得到关于dp/dξ的常微分方程,结合初值条件=0,p=pw,0/p∞(pw,0为原物面压力),逆着来流方向沿截面型线采用隐式龙格-库塔法积分该微分方程可得最终的“有效外形”和压力分布pw(x),详细的求解过程可参考文献[34];

(4)在计算摩阻时,采用White[37]给出的考虑强黏性干扰效应的层流摩阻系数计算公式

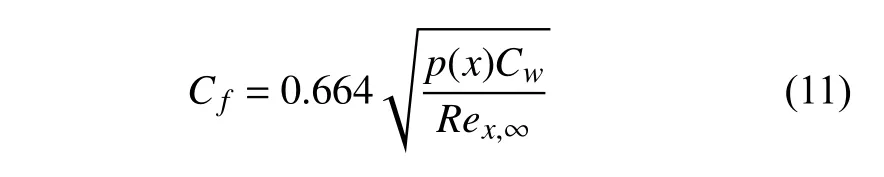
(5)底部压力用来流压力计算;

(6)根据式(9)计算钝前缘表面压力分布;

(7)在求得压力系数和摩阻系数后,通过积分即可获得飞行器的气动力特性,包括升力、阻力和升阻比,其中钝前缘积分只考虑阻力.

3.2 遗传算法

本文参考文献[32]采用标准遗传算法,以参数kw,φ,η为优化变量,以最大升阻比或给定升力下的升阻比为优化目标,进行钝前缘乘波构型优化设计研究,使用轮盘赌的比例选择策略、单点交叉和基本位变异算子.群体规模为30,代数为500,交叉率为0.8,变异率为0.3.此处采用较大的杂交率、变异率和较多的代数以使其尽可能收敛于全局最优解.详细的优化过程见图16.

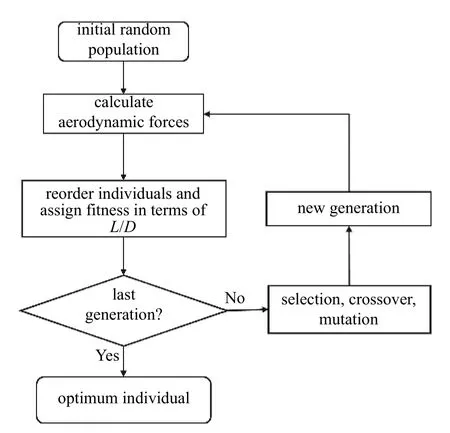
图16 钝前缘乘波构型遗传算法优化过程Fig.16 GA optimization framework of the waverider with blunted leading-edge

3.3 气动力模型验证

在M∞=15,H=50 km 工况下,以升力系数CL=0.2 和钝化半径R=10 mm 约束下的钝前缘最优构型为例,图17 给出了小攻角范围内通过本文采用的简化气动力模型(aero model)和CFD 计算所得的气动力结果对比.从图中可知,与CFD 结果对比,气动力模型低估了升力和阻力,在小攻角范围内气动力模型计算的升力系数、阻力系数和升阻比的最大相对误差分别为5.42%,4.65% 和1.28%,其中2°攻角时升阻比相对误差最大,其原因是:在2°攻角时,简化模型和CFD 求得的升力系数分别为0.161 187和0.166 696,简化模型低估了升力,相对误差为3.31%;简化模型和CFD 求得的阻力系数分别为0.039 629 7 和0.041 510 1,简化模型低估了阻力,相对误差为4.53%,在二者共同作用下,在2°攻角时升阻比相对误差最大,但不超过2%.根据上述对比结果可知,本文采用的工程算法有着较高精度,在飞行器初步优化设计中可以用于快速评估钝前缘乘波体的升阻特性.

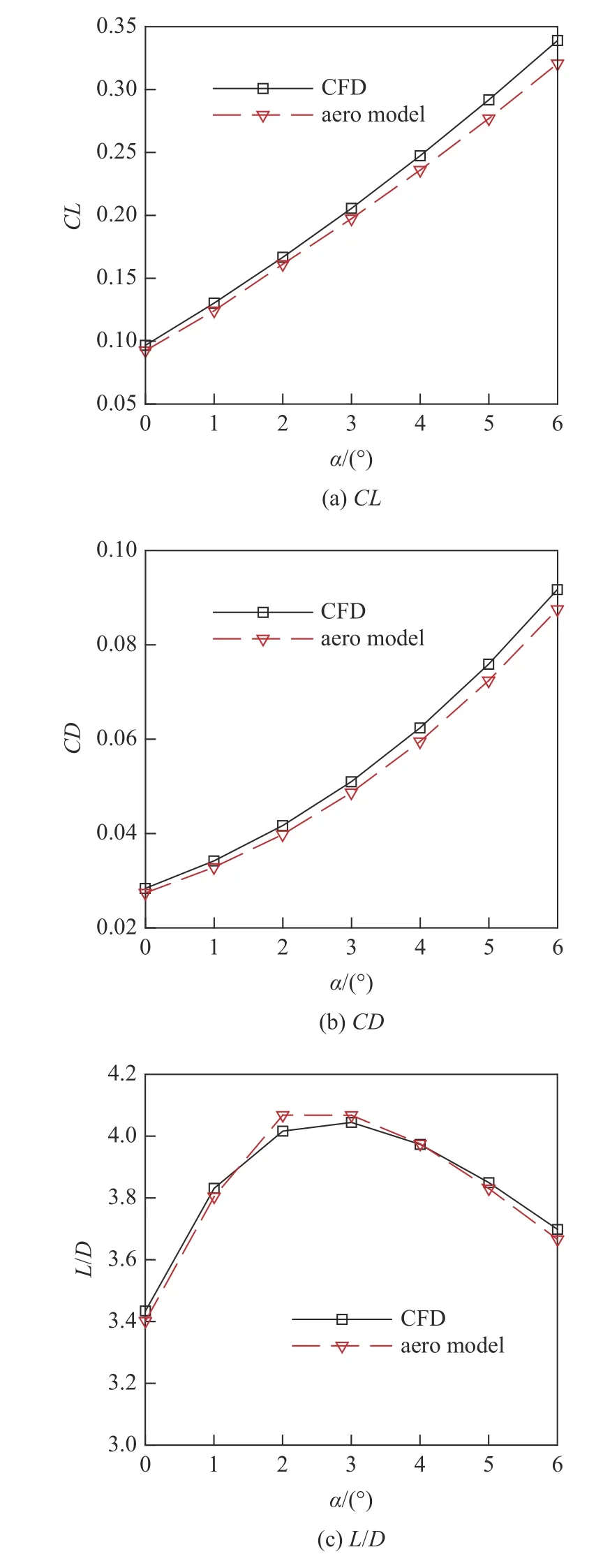
图17 气动力模型与CFD 结果对比Fig.17 Comparison of results calculated by CFD and aerodynamic model

4 结果与讨论

以M∞=15 设计条件为例,优化得到了不同飞行高度、不同升力和不同钝化半径约束下的最优构型.

4.1 最优构型

在M∞=15,H=50 km 设计条件下,以最大升阻比为目标,优化得到尖前缘最优构型和钝化半径R=10 mm,20 mm 的钝前缘最优构型.图18 对比了尖前缘最优构型和不同钝化半径的钝前缘最优构型俯视图和前缘后掠角.从图中可知,尖前缘最优构型(origin-opt)与钝前缘最优构型外形差异较大,钝化半径越大,最优构型越窄,相同纵向位置处的前缘后掠角越大.图19 对比了尖前缘最优构型和不同钝化半径约束下钝前缘最优构型钝化后的升阻比.从图19(a)可知,钝化半径R=10 mm 的钝前缘最优构型(R10-opt)最大升阻比为4.02,相比于origin-opt(3.80)提升5.79%,且钝化半径越大,升阻比提升越显著,在钝化半径R=20 mm 时,钝前缘最优构型(R20-opt)最大升阻比提升高达13.33%.这是因为:由于前缘后掠角分布的差异,钝化后尖前缘最优构型的前缘阻力比重较大,而钝前缘最优构型的前缘阻力比重显著降低,如图20 所示(图中对比了最优构型钝化后钝前缘本身波阻占总阻力的比值),因此升阻比显著提升.

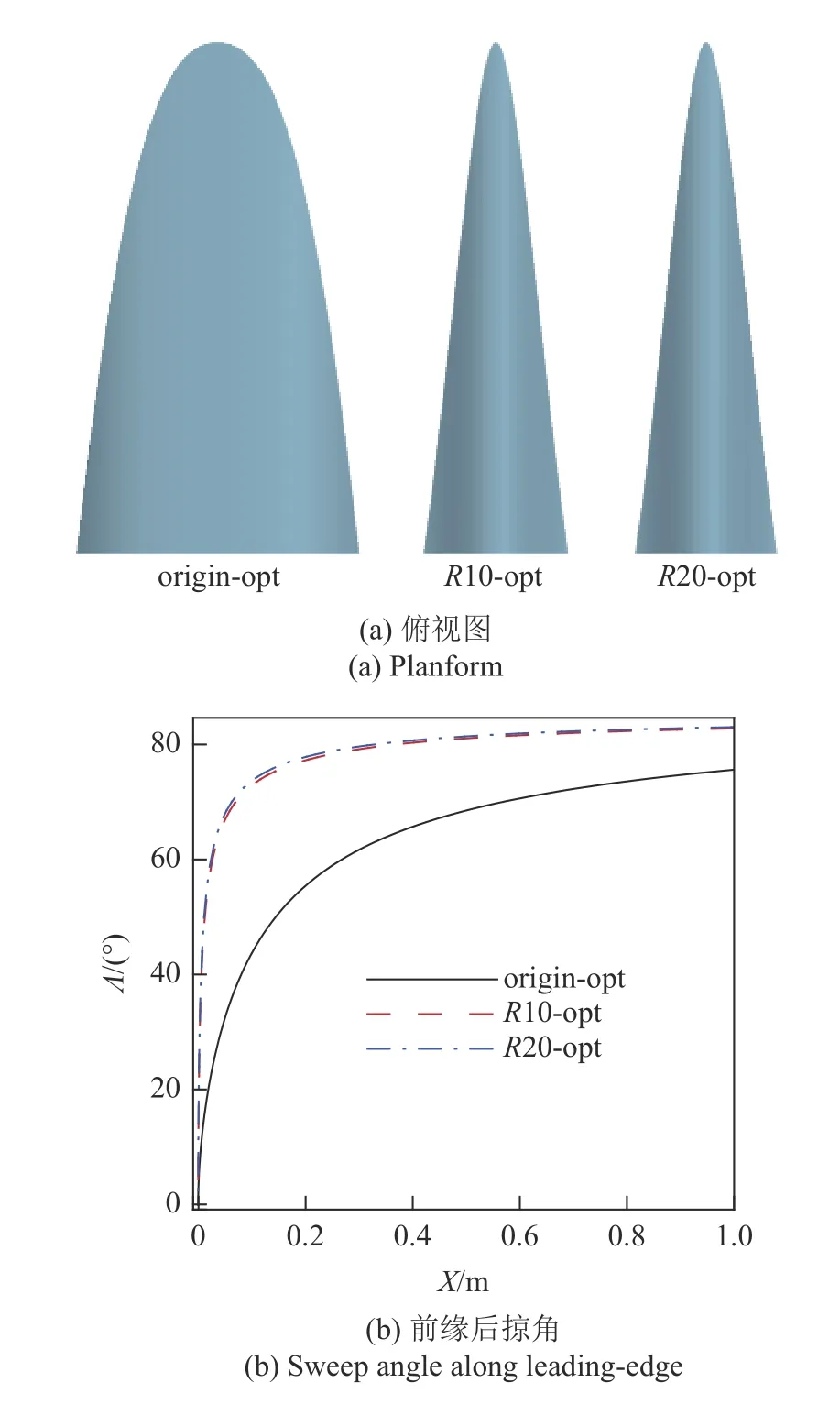
图18 不同钝化半径最优构型几何对比Fig.18 Comparison of optimum configurations

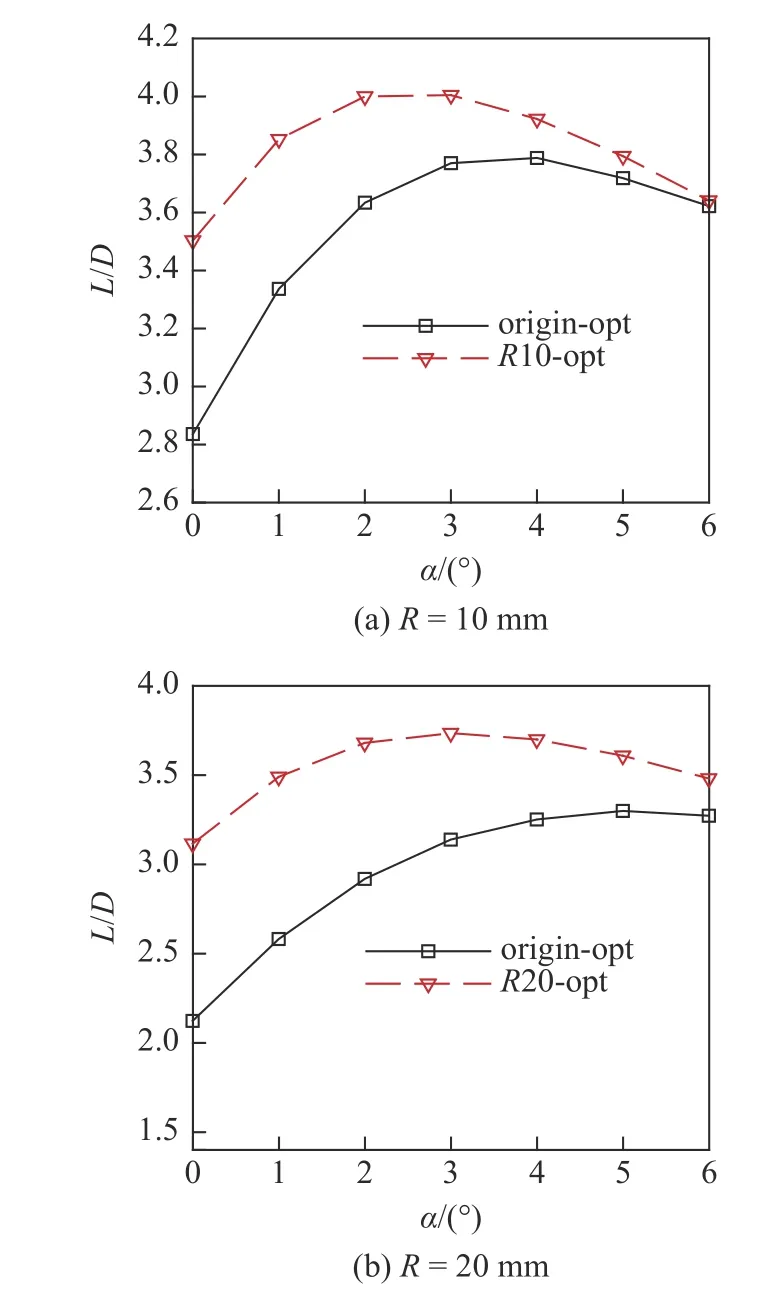
图19 不同钝化半径最优构型升阻比对比Fig.19 Comparison of L/D of optimum configurations

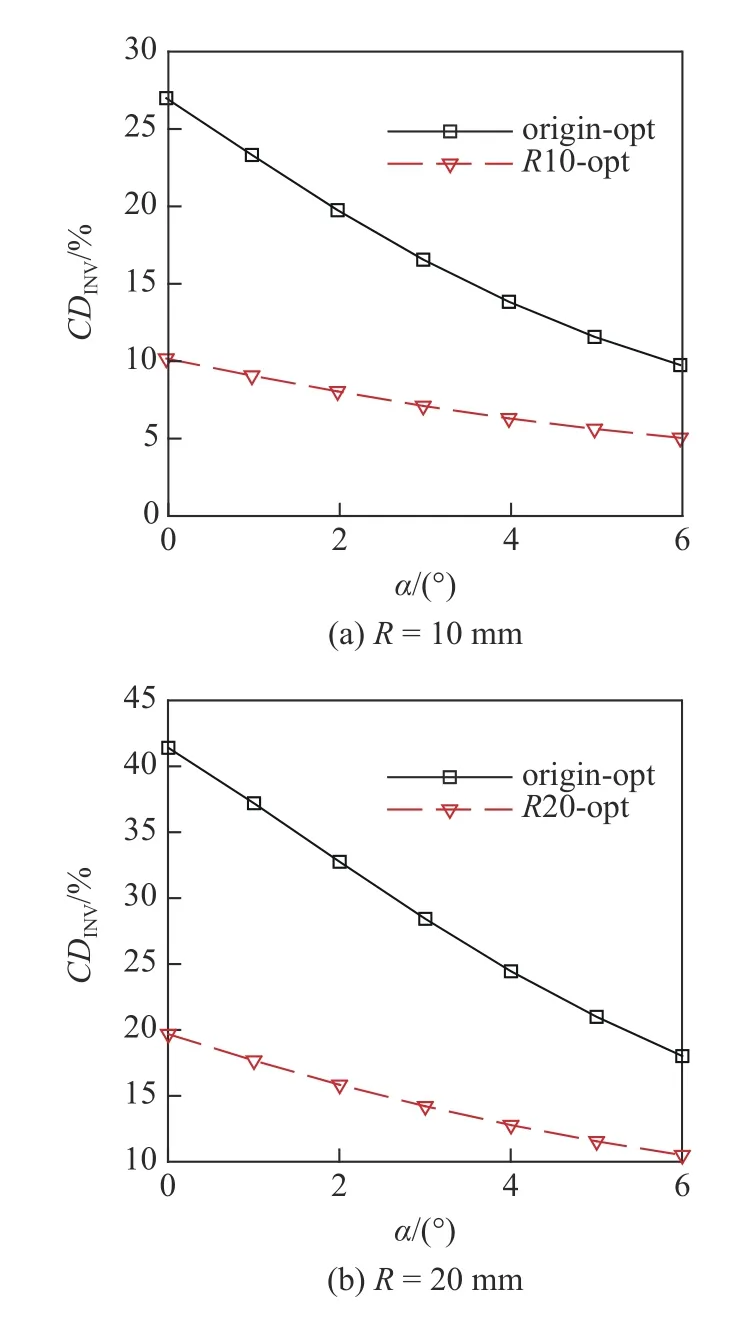
图20 最优构型钝前缘波阻对比Fig.20 Comparison of wave drag of optimum configurations

4.2 不同升力约束最优构型

在实际工程应用中,为满足升重平衡条件,往往需要以给定升力下升阻比为目标开展优化.因此,在M∞=15,H=50 km 设计条件下,首先以CL=0.3 为约束分别优化得到尖前缘最优构型和钝化半径R=10 mm 的钝前缘最优构型,外形对比如图21 所示.图22 对比了origin-opt 和R10-opt 乘波体钝化后的升阻比.从图中可知,在CL=0.3 (设计点)时,R10-opt 升阻比为3.99,相比于origin-opt (3.65) 提升9.32%.

图21 最优构型对比,CL=0.3Fig.21 Comparison of optimum configurations at the condition:CL=0.3

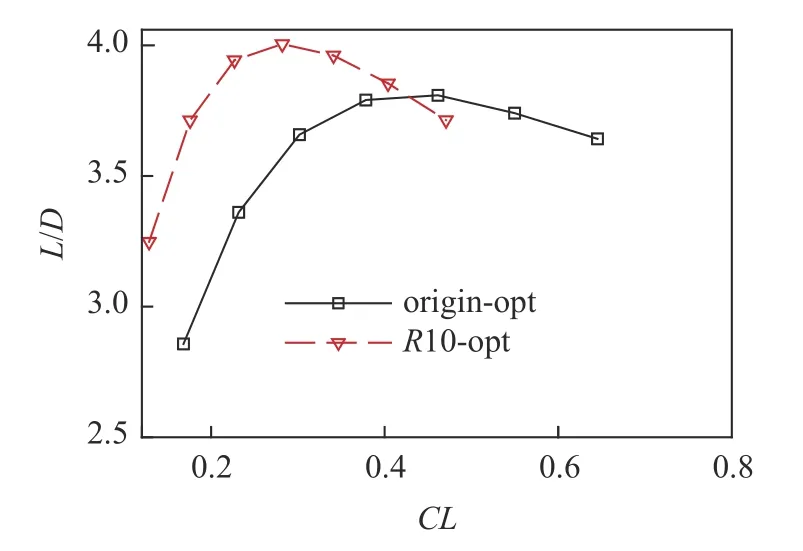
图22 最优构型升阻比对比Fig.22 Comparison of L/D of optimum configurations

图23 和图24 分别对比了不同升力约束下尖前缘和钝前缘优化结果的升阻比和外形.从图23 可知,相同升力约束下,在优化中直接考虑前缘钝化的影响,可以显著提升最优构型钝化后的设计点升阻比,且升力约束或钝化半径越大,升阻比提升越明显.其原因从图24 可知(图中从上至下钝化半径约束依次增加,从左至右升力约束逐渐增大):升力约束或钝化半径越大,尖前缘最优构型与钝前缘最优构型前缘线之间特征差异越大,因此设计点升阻比提升越显著.

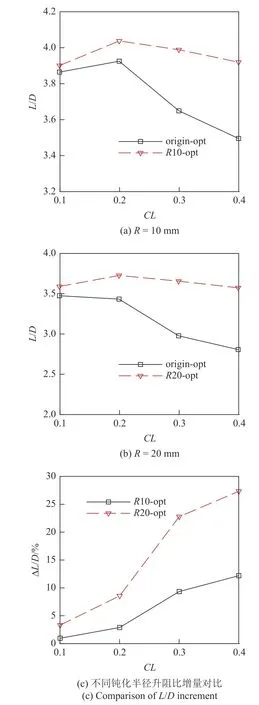
图23 最优构型升阻比对比Fig.23 Comparison of L/D of optimum configurations

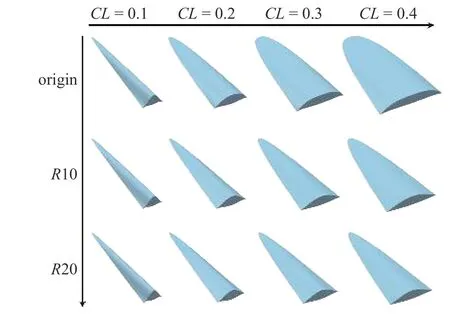
图24 不同升力和钝化半径约束最优构型对比,M15 H50Fig.24 Comparison of optimum configurations at the constraint of different lift and blunt radii,M15 H50

4.3 不同飞行高度最优构型

在M∞=15,H=40 km 设计条件下,以不同升力为约束优化得到尖前缘最优构型和钝化半径R=10 mm 的钝前缘最优构型.图25 对比了originopt 和R10-opt 乘波体钝化后的设计点升阻比.从图中可知,与H=50 km 优化结果一致,升力约束越大,钝前缘最优构型升阻比提升越明显.以CL=0.3 为例,R10-opt 升阻比为4.72,相比于origin-opt(4.04) 提升16.83%.图26 对比了飞行高度H=40 km,50 km 时钝化半径R=10 mm 的钝前缘最优构型设计点升阻比提升量.从图26 可知,当设计马赫数和升力约束相同时,飞行高度越低,钝前缘最优构型升阻比提升越显著.从图27 可以看出,设计马赫数和升力约束相同时,高度越低,摩阻比重越小,尖前缘最优构型越宽,使得其与钝前缘最优构型前缘线特征差异越大,因此钝前缘最优构型升阻比提升越显著.

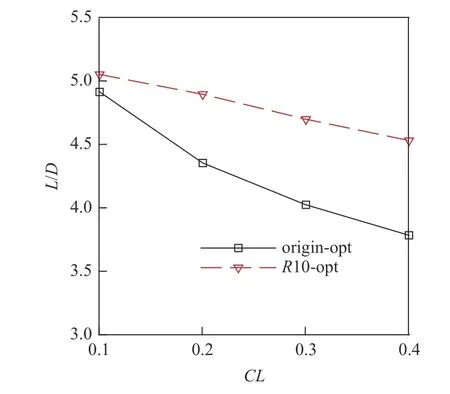
图25 M15 H40 最优构型升阻比对比Fig.25 Comparison of L/D of optimum configurations M15 H40

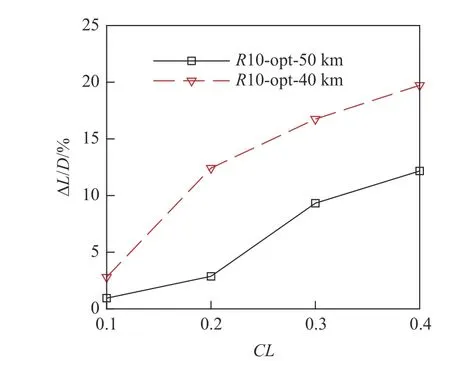
图26 不同飞行高度最优构型升阻比增量对比Fig.26 Comparison of L/D increment at different flight altitudes

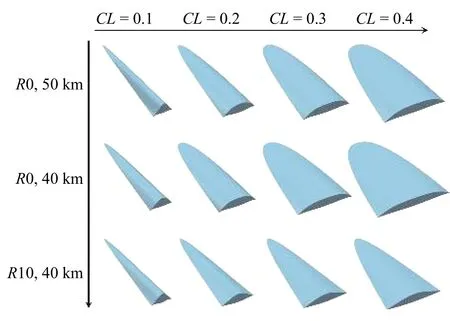
图27 不同飞行高度最优构型对比Fig.27 Comparison of optimum configurations at different flight altitudes

5 结论

本文深入研究了前缘钝化对乘波体升阻特性的影响机理,并以此为基础开展了钝前缘乘波构型优化设计研究,主要内容和结果如下.

(1)前缘钝化引起的乘波体升力降低量较小,阻力显著增加,其中钝前缘本身的波阻在总波阻变化中起主导作用.此外,钝化产生的脱体激波使得乘波体边界层厚度显著增加,边界层内速度梯度显著降低,从而导致上下表面摩阻明显降低,但其摩阻降低量与钝前缘本身的摩阻增加量接近,使得钝化前后乘波体总摩阻增量较小(最大不超过3%).

(2)提出了一种评估钝前缘乘波体气动力的近似方法,即在评估钝前缘乘波体气动力时,采用修正的牛顿理论计算的钝前缘本身的波阻作为总阻力变化量,并忽略钝化对乘波体升力的影响.根据该方法,结合遗传算法优化得到了钝前缘乘波体最优构型.

(3)在M∞=15,H=50 km 设计条件下,无升力约束下优化得到尖前缘最优构型和钝化半径分别为10 mm,20 mm 的钝前缘最优构型.R=10 mm 时,钝前缘最优构型最大升阻比提升可达5.79%,且钝化半径越大,钝前缘最优构型与尖前缘最优构型差异越大,最大升阻比提升越显著.

(4)在M∞=15,H=50 km 设计条件下,以不同升力为约束优化得到尖前缘最优构型和不同钝化半径的钝前缘最优构型.当CL=0.3 时,钝化半径R=10 mm 的钝前缘最优构型相比于尖前缘最优构型简单钝化的升阻比提升量可达9.32%;且升力约束或钝化半径越大,钝前缘最优构型设计点升阻比提升越明显.

(5)在M∞=15,H=40 km 设计条件下,以不同升力为约束优化得到尖前缘最优构型和钝化半径R=10 mm 的钝前缘最优构型.在CL=0.3 时,钝前缘最优构型升阻比提高16.83%;对比H=50 km 优化结果可知,飞行高度越低,钝前缘优化结果的升阻比提升量越大.

在未来的研究中,可以在优化过程中定量考虑前缘钝化对乘波体上、下表面压力分布的影响,并引入配平及稳定性等约束条件,得到更接近工程应用需求的钝前缘最优乘波构型.