AGV车体减振机构稳定性研究
2022-06-16张晓燕
张晓燕
(浙江长征职业技术学院,杭州 310023)
0 引言
随着纺织产业结构调整、技术发展以及用工难、用工贵等问题的日益凸显,无人搬运车系统(Automated Guided Vehicle,简称AGV)以其灵活机动、智能精准等特点越来越受纺织企业青睐,也逐渐成为纺织智能工厂的标配。AGV搭载有光学、电磁或智能激光导航系统,能够自动或手动沿着规划路径,进行工位与工位、工位与仓库、仓库和仓库之间的货物搬运及仓储工作。AGV减振系统是车架与车桥之间的弹性连接机构,通过该系统可互相传递车架与车桥之间的力和力矩,缓和载荷冲击,减少车体跳动,使小车平顺安全行驶。
AGV减振系统设计不合理将严重影响其功能的实现。一方面,由于该系统通过伺服电机驱动,电机转速及方向将通过AGV控制器精准计算,若减振系统设计不合理,引起车轮打滑和跳动,将严重影响AGV运行精度。另一方面,AGV通过激光、磁条等方式导航,当路面不平或有障碍物时会引发AGV车体横倾和纵倾的问题,对AGV导航产生较大影响或使车体偏移目标路线,严重情况下甚至发生碰撞等危险情况。因此,AGV减振机构设计需遵循以下原则:① 轮系同地性,须保证所有驱动轮共同接触地面,防止驱动轮打滑;② 驱动轮产生的驱动力应大于其运行阻力;③ 减振机构在保证尺寸的条件下,应加大驱动轮纵向伸缩范围,以适用于各种复杂路面,且应具有吸振、防侧翻功能。较为合理的减振系统,是AGV设计的重点。
1 AGV减振系统模型
鉴于AGV减振系统对其运行稳定性有严重影响,相关研究者对此做了大量的工作。如:韩乐列举了各类不同AGV减振浮动机构,并提出该机构的设计需求[1];方春富通过比较有、无悬架减振机构移动机器人的振动情况,结果表明悬架结构具有良好的隔振效果,垂直振动加速度减少约80%[2];周益林等为保证AGV运行可靠性,通过ADAMS软件建立AGV受力模型,最终验证所设计AGV减振机构的合理性[3]。下文笔者将基于Matlab对目前较为普遍的2种AGV减振机构进行设计,并在不同路面激励下建立多自由度振动系统,以计算、比较车体在不同系统中的振动情况,为AGV的悬架设计提供技术引导。
图1为目前较为普遍的2种AGV减振方式,两者均为六轮结构,中轴放置驱动轮,车体前后各放置2组万向轮。
在如图1a)所示的杠杆原理减振机构中,前后轮通过杠杆相连,支点与车身相连,该结构可保证驱动轮时刻触地,且驱动轮所受压力可随车身质量等比增加,防止出现打滑,复杂路况下可减少车辆跳动;缺点为前后轮振动会互相影响,且结构较为复杂。
图1b)所示的六轮独立减振机构,优点是振动互不干涉;缺点为驱动轮与地面摩擦力仅受车身弹簧影响,AGV在满载时驱动力不能随负载增加而增加,存在空转的可能性。

a) 杠杆原理减振 b) 六轮独立减振图1 2种AGV减振方式
由于车体振动机制主要由悬架方式及各减振单元性能决定,合理设计并选择各系统参数,将对提高AGV行驶平顺性至关重要。张军等人设计分析如图1b)所示的悬挂系统[4],并通过结构分析和实验验证其稳定可靠性,发现当AGV行驶速度相对较小且处于低频振动时,振动位移将清晰反映振动强度的大小。
2 减振机构振动模型
路面信息为该AGV振动主要激励输入,笔者利用功率谱密度Gq(n)(也称路面不平整系数)构建路面信息。 则:
(1)
式中:
n——空间频率;
n0——参考空间频率;
W——频率系数。
通过模型进行整体振动研究,需进行如下假设:在AGV小车振动模型中,前后万向轮与车体之间均具有减振弹簧,且都具有摩擦阻尼;万向轮和驱动轮均近似为无阻尼弹簧;AGV车体与减振机构及车轮均为刚性连接;AGV左右结构对称,车体质心位于对称轴上,且两侧的前、中、后轮均位于同一直线;杠杆原理减振和六轮独立减振机构均为九自由度振动系统,即4个万向轮和2个驱动轮竖直跳动,以及车体的竖直、俯仰和倾斜振动。
2.1 杠杆原理减振机构中车轮对车体的作用力
2.1.1根据刚体转动原理,计算杠杆原理减振机构各车轮对车体的作用力为:
F2=CRQ×(US2-U2)
F5=CRQ×(US5-U5)
式中:
CR——万向轮与车体之间弹簧弹性系数;
R1~R6——分别为车体左前、左中、左后、右前、右中和右后位置;
UR1~UR6——车轮与车体连接处的运动位移;
RR——万向轮与车体之间弹簧阻尼系数;
U1~U6——各车轮的位移;
CRQ——驱动轮弹性系数;
S2,S5——杠杆原理减振机构中左右两侧的杠杆支点;
US2,US5——左、右驱动轮在杠杆支点处的位移。
2.1.2杠杆原理减振机构的竖直振动、俯仰和倾斜以及杠杆转动的微分运动方程为:
MA·ÜA=F1+F2+F3+F4+F5+F6
(F4+F5+F6)
L1·(F5+F6)
式中:
MA——车体总质量;
UA——车体运动位移;
θ,Jθ——车辆倾斜角度及其转动惯量;
φ,Jφ——车辆俯仰角度及其转动惯量;
γ,Jγ——右侧杠杆转动角度及其转动惯量;
β,Jβ——左侧杠杆转动角度及其转动惯量;
L1~L5——车体质心与车轮的距离,见图1。
2.1.3杠杆原理减振机构内前万向轮与驱动轮位于杠杆两端,其相对于车体位移方向相反,AGV各车轮位移方程为:
U1=UA-L5·sinθ-L1·sinφ+L3·sinγ
U2=UA-L5·sinθ-L1·sinφ-L4·sinγ
U3=UA-L5·sinθ+L2·sinφ
U4=UA+L5·sinθ-L1·sinφ+L3·sinβ
U5=UA+L5·sinθ-L1·sinφ-L4·sinβ
U6=UA+L5·sinθ+L2·sinφ
2.2 六轮独立减振机构中车轮对车体的作用力
2.2.1六轮独立减振机构中车轮对车体的作用力计算公式为:
式中,RRQ为驱动轮阻尼系数;其余同前。
2.2.2六轮独立减振机构中各轮为独立振动,其侧倾、俯仰微分运动方程为:
MA·ÜA=F1+F2+F3+F4+F5+F6
(F4+F5+F6)
(F5+F6)
2.2.3六轮独立减振机构中各车轮位移方程为:
U1=UA-L5·sinθ-(L1+L3)·sinφ
U2=UA-L5·sinθ-(L1-L4)·sinφ
U3=UA-L5·sinθ+L2·sinφ
U4=UA+L5·sinθ-(L1+L3)·sinφ
U5=UA+L5·sinθ-(L1-L4)·sinφ
U6=UA+L5·sinθ+L2·sinφ
分别将车轮受力、位移等方程带入受力方程中,即可得到AGV不同减振机构的多体振动方程。
3 结果分析
在AGV行驶方向的右侧轮行驶于较为平整的路面时,其最大幅值为2.8 mm、长度为10 m,AGV的行驶速度为1 m/s;在AGV车体所行驶的左侧路面较差时,其最大幅值为15 mm。设AGV总质量为200 kg,笔者通过Matlab进行模拟计算,利用精度较高的ode45方程进行微分方程的求解,模拟出如图2和图3所示的结果。

图2 AGV车体在不同万向轮弹性系数下的振程

图3 AGV车体在不同万向轮阻尼系数下的振程
比较图2曲线可知,AGV在首次迎接较大路面激励时,具有较小万向轮弹性系数的车体拥有较好的吸振能力,但该车体也因弹簧变软出现剧烈晃动。随着万向轮弹簧系数的合理增加,车体吸振能力减弱,但车体则在随后的振动中表现出较好的稳定性,当弹性系数加大到127 500 N/m时,车体的稳定性急剧变差。因此,万向轮弹性系数过大或过小的选择都将增加车体在运行过程中的不稳定性。观察图3可知,在车体经过较大路面激励后,车体振动随着阻尼系数变小而增加。
AGV杠杆原理减振机构是通过杠杆连接驱动轮与前万向轮,其六轮机构可确保该AGV驱动轮与路面接触,并且随着负载增加,驱动轮与地面摩擦力也随之增加,AGV车体垂直动态性能将由杠杆支点以及后轮振动特性决定,且杠杆支点瞬时振程将受前轮和驱动轮合成影响,因此该类型减振机构将缓和车轮受到的瞬时冲击。此结论也可通过图4得到证明,AGV车体振程在行驶距离为3 m和9 m处,均出现较大波动;相比之下,杠杆减振机构冲击较为缓和,在3 m处杠杆减振机构比六轮独立减振机构的车体振程减少约15%,在9m处有50%以上的减少量,减振效果明显。
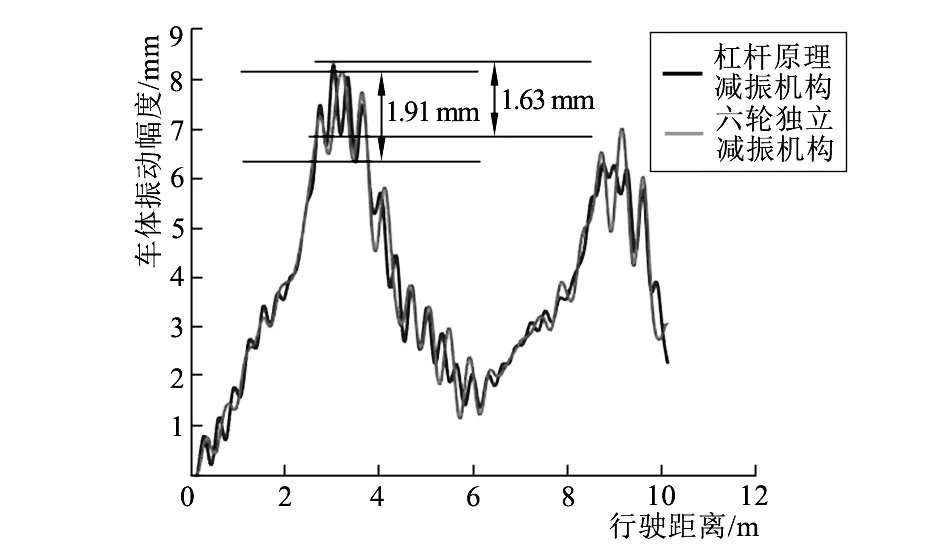
图4 车体在不同减振机构下的振程
4 结论
4.1通过比较AGV的2种不同减振系统,发现利用杠杆原理实现的减振系统比六轮独立减振系统的稳定性更好,车体振动相对较为平缓,且驱动力矩可随负载增加而增强,对今后AGV减振机构设计具有指导意义。
4.2采用万向轮弹性系统对AGV车体具有吸振效果,合理选择弹性系数可提高搬运车行驶的稳定性和平顺性,准确计算弹性系数是设计AGV减振系统的重要环节。
