基于单目机器视觉的实时船舶测距方法及误差修正*

徐 进 陈姚节

（武汉科技大学计算机学院 武汉 430081）

1 引言

视觉测距［1］作为机器视觉［2］领域内的基础技术之一而受到广泛的关注，其广泛应用于机器视觉定位［3］、目标跟踪［4］、视觉避障［5］等。船舶作为水上运输的交通工具，同其他的交通工具比较，不具有很强的灵活性和可控性，需要提前测量与其他船舶和碰撞物之间的距离，并做好规避方案，才能有效地避免碰撞事故的发生。机器视觉的发展为解决海上船舶测量提供了一个新的方向。通过现有船舶上的摄像头来模拟人的视觉功能，对“目标图像”进行数字化，提取相应信息，并通过计算机进行相应处理，来实时获取船舶的位置信息和速度。

传统非机器视觉测量船舶距离的方法主要包括雷达自动识别系统［6～7］、船舶自动识别系统［6］、红外传感器测距方法［8］和超声波测距方法［9］等。雷达自动识别系统和船舶自动识别系统都是保障船舶安全航行，避免碰撞的有效方式，但现有设备昂贵，我国仅在大型船舶上配备，很难大范围普及。红外传感器测距方法是通过发射红外光以及接收的红外光来判断目标船只和本船的距离，在中短距离的判断上具有较大优势。但精度不高，容易同其他红外信号混淆，造成系统失效。超声波测距方法适用于中小型船舶的距离测量系统，但受天气的影响特别大，特别是浓雾天气。

基于机器视觉的测量方法［10］主要包括：单目视觉测量、双目视觉测量、结构光视觉测量等。结构光的应用受到光源的限制［11］，本文无法应用，这里不做介绍。王健等提出一种在AOI 内利用灰度梯度探测物标的方法，但船舶动态摇摆对该方法的测距精度影响较大［12］。杨晨曦等提出一种双目立体视觉测距方法，该方法测距精度高，但可测量距离短［13］。而单目视觉测距方法具有结构简单，操作方便，运行速度快等特点。本文在单目视觉的基础上进行研究。

2 单目视觉测距原理

2.1 系统流程

基于单目机器视觉的实时船舶测距方法及误差修正是通过Visual Studio 2017 平台开发设计、计算机视觉库OpenCV实现功能、SCA200光电云台采集图片并进行重复性试验，采用faster R-CNN 算法和ECO 算法实现对目标的识别与跟踪，并画出矩形框，使用三角几何原理对目标进行测距，并通过误差修正方法对误差进行调整，最后输出测距结果，整个系统的流程如图1所示。

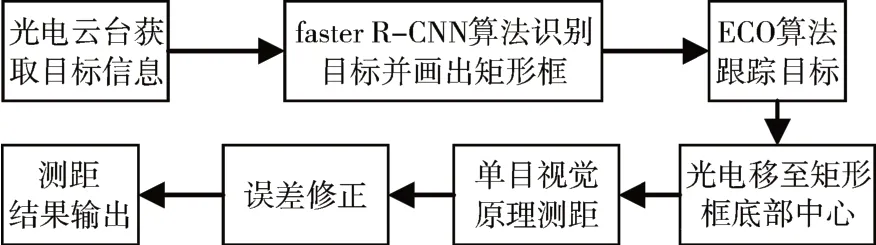
图1 单目测距流程图

2.2 测距原理

光电云台获取目标船舶的二维信息，通过机器视觉faster R-CNN 进行目标检测，提取目标船舶的特征，根据船舶形状框选目标，并将光电中心（即为图像中心）移到目标底部中心，利用三角几何原理计算与目标船舶之间的距离。

点P 为光电云台，线段PF 为光电云台初始水平方位，矩形ABCD为自动船舶的目标框，点S为船舶矩形框底部AB的中心点，h为光电云台距离水平面的安装高度OP，d为本船舶与目标船舶之间的水平距离OS，角α为光电云台的俯仰角，其中f为光电云台的有效焦距。(u0，v0)为光轴与像平面的交点，作为像平面坐标系的原点，取为( 0 ，0 )；(u，v)为目标船舶底部中心点S在像平面上的投影坐标。

图2 单目测距几何模型图

根据几何三角原理，其距离计算公式为

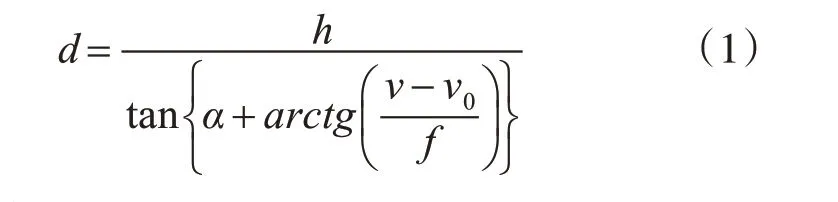
图像坐标系与屏幕坐标之间有如下关系，其中dx，dy 为每一个像素点在x 轴与y 轴方向上的物理尺寸。(u0，v0)为屏幕坐标中心点，为相机的内参，可通过相机标定获取。中心点S 在像平面上的实际投影点与屏幕中心点之间的关系如式（2）。

3 误差分析及误差修正方法

3.1 误差分析

摄像机镜头的几何畸变和船舶摇摆等问题一直是船舶测距中的重难点。本文根据光电云台与船舶位置是否发生偏移将误差分为静态误差和动态误差两种，并分别对误差因素进行分析。静态误差：1）摄像头几何畸变造成目标成像位置的偏移误差；2）光电云台的安装高度误差；3）光电云台在跟踪目标时存在的抖动误差；4）图像处理中的噪声误差以及根据目标轮廓自动检测形成矩形框所造成的误差；动态误差主要是由于船舶摇摆造成的光电云台高度以及初始角度发生的偏移误差。

由式（1）可得，测量距离与相机的安装高度成正比即d=k·x，k⊂R。即可表示为在同一偏转角度，随着光电云台安装高度的增加，所产生的距离误差不变。如图3 所示，相机的安装高度对距离计算误差影响为固定值，因此本文这里不做分析。

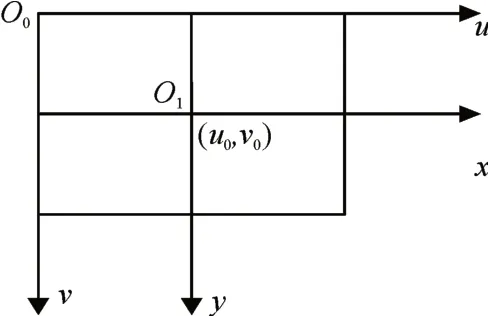
图3 屏幕坐标投影

图4 相机安装高度对距离影响图

3.2 静态测距试验

首先进行静态试验，光电云台安装高度为2.0m，计算3m～20m之间的距离，测量数据为16组。通过光电云台沿着某一方向采集图片，连续采集目标船舶的图片。光电云台在自动跟踪目标时，光电本身存在抖动误差这种误差是客观存在的。假设光电云台抖动误差角度为θ，此时距离计算公式为

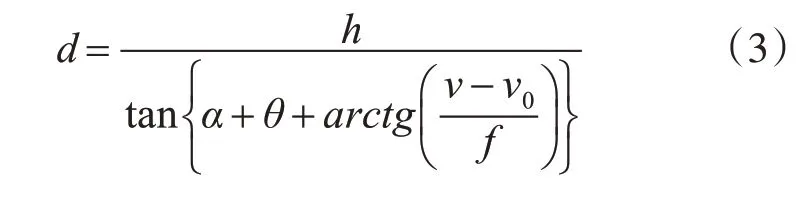
光电云台在跟踪目标时，会随着目标检测的变化在矩形框内上下移动，导致测距的角度也在小范围的变化。本文采取求和计算平均值法来计算距离。具体方法为每隔10 帧计算与目标的距离并求和来消除光电云台抖动误差角度θ，计算距离为这10帧的平均值。

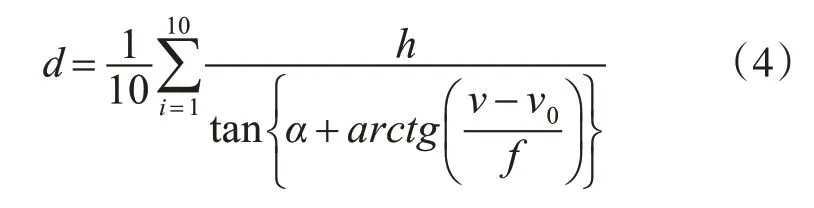
通过静态试验误差分析对数据进行修正，得到的修正后的数据如表1所示。

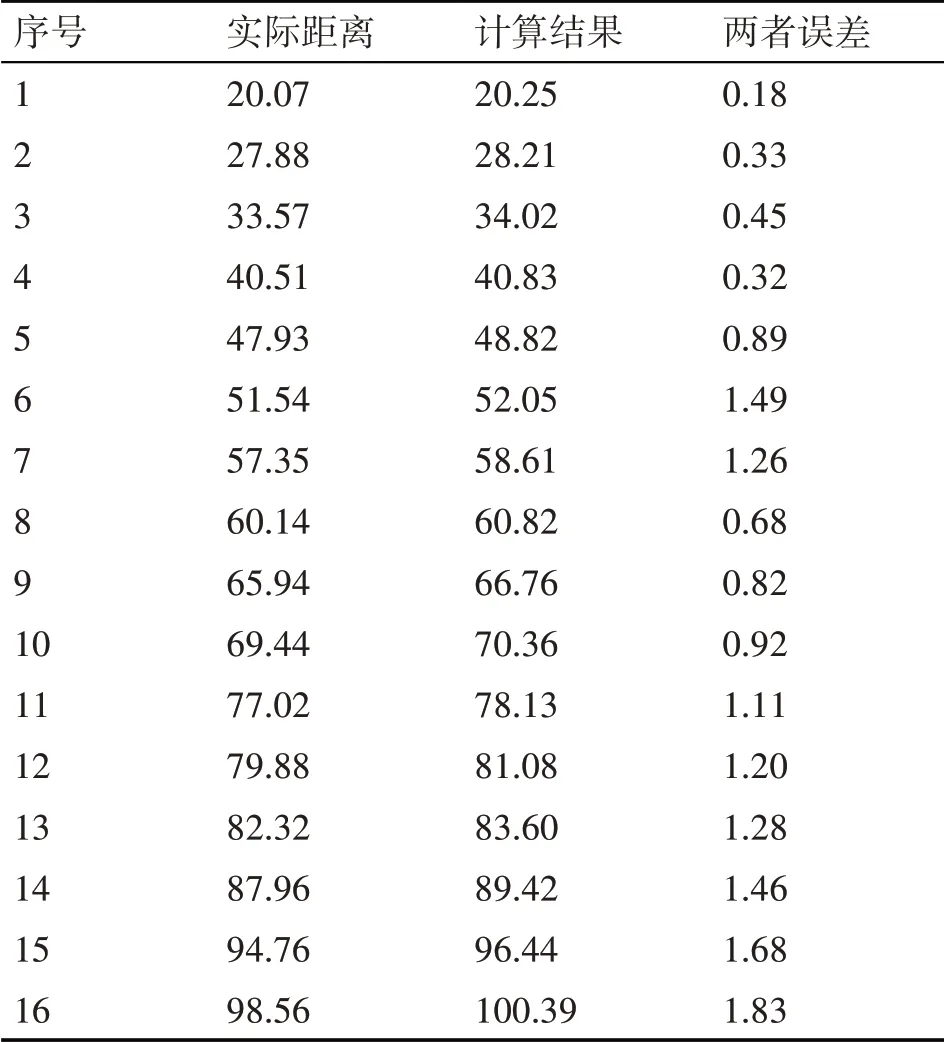
表1 静态测距实验结果（单位：m）

从表1 可以看出，利用本文提出的静态误差修正方法，在100m 内，实际距离与测量误差在2m 之间，在可接受范围内，说明本方法测距具有一定的可行性。

3.3 动态测距试验

当船舶在水面上进行动态运动时，其测量的横倾角会随着船舶摇摆而改变。不同船舶最大横倾角要求不同，这里考虑的船舶横倾角在5°以内。船舶受波浪影响造成前后摇摆，此时会有以下情况：因无法获取目标船舶摇摆角度。由于单目视觉会失去空间角度信息，这里只考虑本船舶摇摆中的前倾而导致光电云台的高度以及俯仰角会发生变化，假设船舶前倾偏转角为γ。通过陀螺仪实时获取船舶前倾角度。则此时光电云台相对于水面高度为

这里假设船舶前倾角度为正，后摇角度为负。此时距离计算公式为

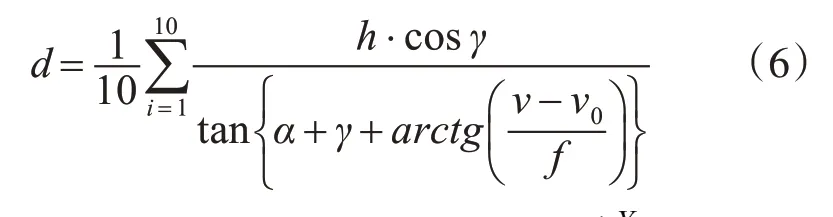
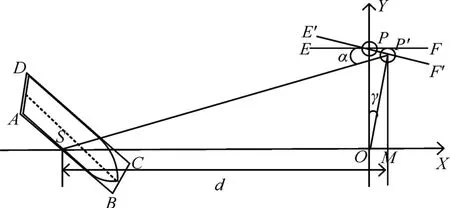
图5 船舶震荡角度变化图

验证实验分为两组，第一组为摇摆状态下物体静止测距实验，即保持目标位置不动，距离不变。第二组为摇摆状态下物体进行在直线移动时动态测距实验，保持物体沿着光电云台正前方移动，同时使光电云台在（-5，5）范围内摇摆。实验对比共有四组：实际距离相同、横倾角不同的两组：27.88m和69.44m；实际距离不同、横倾角相同的两组：-2.9655°和-4.6892°。实验结果表明，本文提出的基于单目视觉测距系统的实时船舶测距方法及误差修正方法能够很好地降低相对误差，且具有很高的可行性。从测量的数据观察，使用本文提出的修正方法测距的相对误差保持在（0.4%～2.7%）之内，修正前相对误差在（16.2%～79.2%）之间。说明本文的修正方法，极大地减少了相对误差，提高了测距精度。且本文的修正方法相对误差整体保持在3%之内，说明该方法效果较稳定，具有很好的可行性。

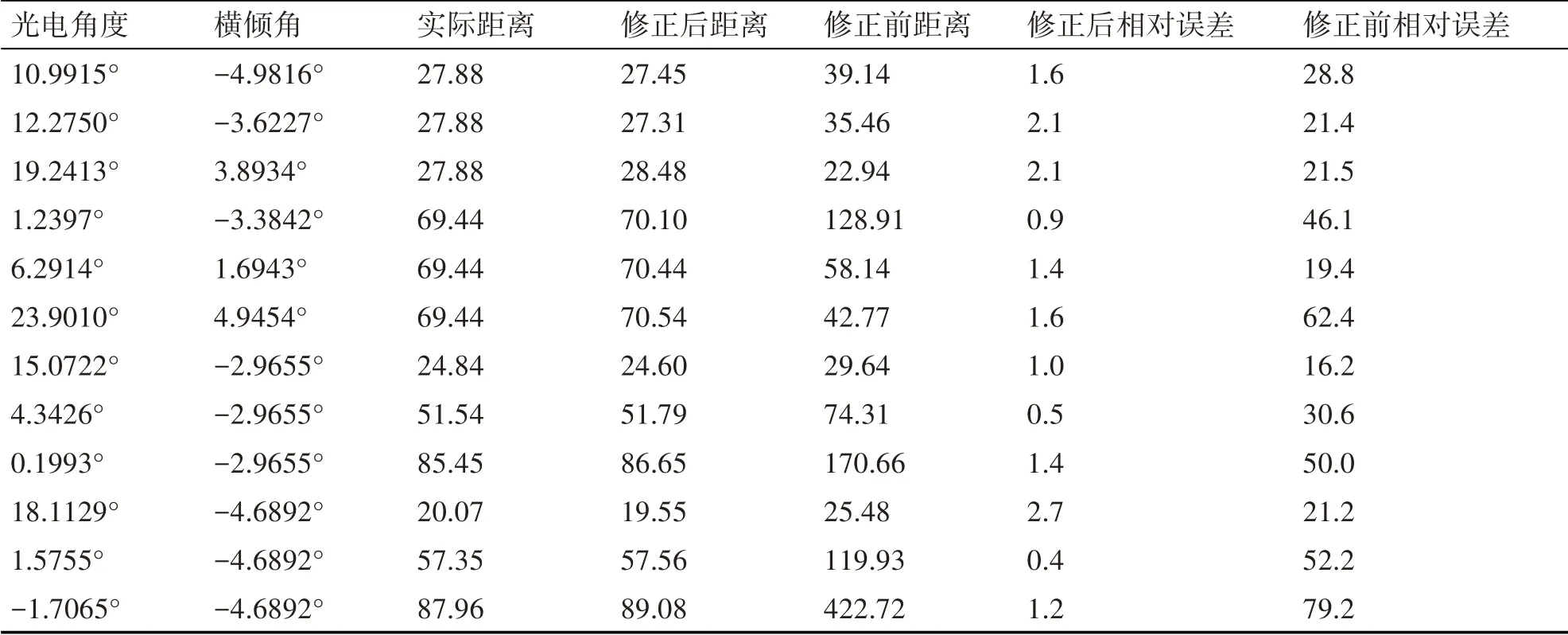
表2 摇摆状态下的动态测距实验结果

4 结语

本文对单目视觉在船舶距离测量领域的应用进行了研究，提出了一种改进方法和误差修正方法。其改进方法是在传统的单目视觉测距基础上，将光电云台光心移至目标矩形框的底部中心处，对目标物体进行测量。并通过误差修正方法对测量结果进行修正，使用修正方法之前，相对误差在（16.2%～79.2%），而本文的修正方法使测距相对误差保持在（0.4%～2.7%）之间，极大地提高了测距精度，具有很好的可行性，可以让船舶工作人更直接地了解前方障碍物距离信息，及时作出应对措施以避免碰撞事故的发生。