用于便携定位装置的逆地理编码算法研究

张 伟，于 静，陈儒敏，张鸿博

（北京科技大学天津学院信息工程系，天津 301830）

关键字：便携定位装置、逆地理编码算法、传统搜索算法、k-d树算法

0 引言

当前，随着移动互联网基建设施的逐步完善和智能手机、平板等终端设备的普及，基于智能终端的APP 应用程序获得爆发式增长，其中绝大部分业务都需要使用设备的地理位置信息。同时，由于国内经济的发展和人民生活水平的提升，私家车驾车出行的比例大幅上升。驾驶员普遍应用高德地图、腾讯地图等移动导航APP 软件。通过使用此类软件，司机往往能够快速知晓车辆所处具体位置，获得其经纬度坐标，并能够进行路径规划等高级操作。

然而，这类应用有一个弊端，即必须在联网的情况下才能使用。目前，在我国通讯基站实施覆盖的平原城市、乡村等地区，实时使用此类软件的问题不大；但在突发或者特定情况下，通信网络的获取比较困难：比如，在地质勘探工作者进入深山和原始森林进行科学考察时，或者突发地质气象灾害时，由于不具备通讯基站等通讯设施，这类导航软件往往不能正常使用。

针对这类无网络情况下的定位需求，本文提出了一种基于k-d 树的逆地理编码算法，此算法应用场景定位于便携式离线定位装置上。同时，编写基于欧氏距离和半正矢公式的两种传统搜索算法代码，作为对照组。通过测试，不仅验证了k-d 树算法的正确性，而且证明在较大测试集的情况下，此算法运行效率比传统算法高出近300倍。

1 逆地理编码算法的研究现状

逆地理编码算法，亦称反地理编码算法，或地址解析算法，是指从已知的经纬度坐标推算出对应的地址描述的转换算法。一般用于根据定位点经纬度来获取该处的位置详细信息，在地质考察、野生动物保护、军事等领域有着大量的应用场景。目前，大部分系统和项目开发中，逆地理编码算法都是通过调用互联网厂商提供的逆地理编码服务接口来实现的。国内市场占有率较高的厂商，例如百度地图和高德地图，均推出了基于开放地图服务的地图API接口。文献［1］中详细阐述了如何通过编写JavaScript 脚本程序调用高德开放地图接口，输入经纬度得出地理信息的过程。国外的诸多网站，如PickPoint、GeoNames、MapQuest等服务商也提供类似的服务。

然而，在上述提到的某些应用场景中，离线逆地理编码算法的实现又是不可回避的要求。目前，国内外对逆地理编码具体算法实现及流程的研究很少，大多数只是调用现成的程序接口或者封装好的模块。高德集团的一份专利中，提及了离线的逆地理编码的方法及其装置，不过其侧重于设备端的功能设计及实现，对具体的算法实现流程并未进行深入的阐释，可参考价值有限。文献［3］提出了一种基于GeoHash算法的分层调度方法和区间调度模型，可对共享单车的调度方案进行有效地规划，通过对比已有的分层调度方案，得出了算法收敛速度快、模型时间复杂度低的结论。但是，该文章直接调用封装好的第三方GeoHash计算模块，未对其实现机理做详细研究。针对上述不足，本文将逐步通过问题分析、测试集收集、测试组/对比组代码测试等流程来研究这一问题。

2 问题的分析

离线逆地理编码算法的流程，简单来说，即是在未联网的情况下，从便携式离线定位装置的GPS 接收器获取一个或多个经纬度数据，再由算法与内置数据集进行搜索和比对，得出距离所测数据点最近的内置地址数据，然后将结果数据以地理名称的字符串形式返回。该计算流程涉及两方面关键问题，即：①内置数据集的来源、数据格式和参考点位的数量级；②搜索算法的计算效率和正确性。下文将逐一进行简述。

2.1 内置数据集

本文算法的应用范围先限定为国内区域，数据集采用国家标准行政地理区划中的国内行政区划不同粒度范围地名划分机制，具体信息如表1 所示。

表1 国内行政区划分级划分机制

根据表1定义本文所用的地址数据结构，如表2所示。

表2 地址数据结构

其中，scale_int 取值范围为1～6，表征该条数据的地址级别；lon_f、lat_f，使用浮点数记录地址的经纬度信息；add_1～add_6，记录地址要素的字符串，比如add_3取值街道名称，上限为256个字符。

本文的数据集取自国家统计局2020 年公布的数据，分别获取3/4/5 级行政区划数据用于后续测试。经过清洗后的数据个数如下：3级数据3552 个，4 级 数 据42358 个，5 级 数 据758050个。从3 级数据中随机抽取296 个作为测试数据，以便验证算法的正确性。因此，3级行政区划数据用于内置数据集的个数变为3256 个。下文中，主要应用3 级行政数据验证算法的正确性，4级、5级行政数据测试算法的执行效率。

2.2 基于经纬度数据的距离计算

在计算给定坐标点具体属于哪个地理区划时，最直接的办法是计算此点与内置数据集全部参考数据点的距离，并排序选出最小的点，以此作为所属地理区块划分。当然，考虑到行政区划边界不是严格的与经纬线平行的直线，还需要综合附近多点的计算结果进行判断。本文将问题简化，以距离计算为基本算法进行逆地理编码研究。

图1 中，点是已知点，点是所求点，点是地球球心，、两点间的弧线表示球面距离。

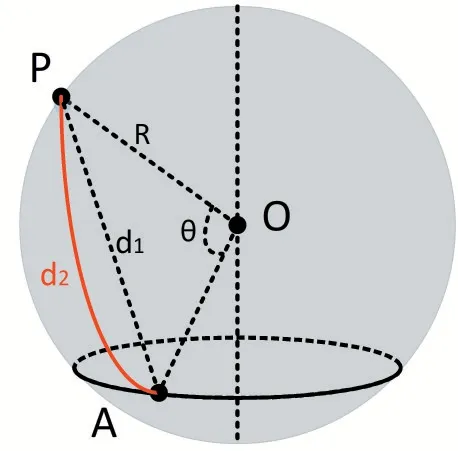
图1 球面两点间距离计算示意图

计算距离的算法有多种，一为欧拉公式（Euclidean Distance），计算与点的直线距离，如公式（1）所示。

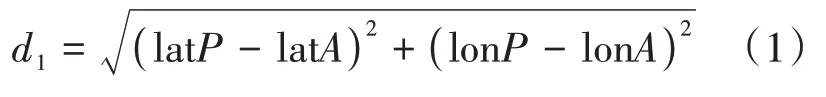
考虑到地球是个球面，第二种采用半正矢公式（Haversine Formula）计算球面上两点间的距离，推导过程如下所示。

对于球面上任意两点，圆心角的半正矢值（）可用公式（2）进行计算。

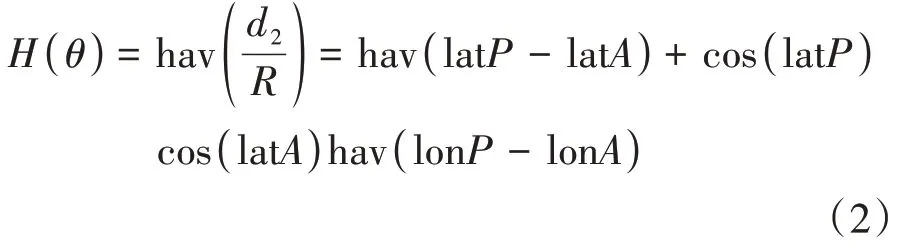
公式（2）中，代表弧度制圆心角；代表地球半径，取值6378 千米；(lon,lat) 和(lon,lat)分别代表球面上任意两点和的弧度制经纬度坐标，其值采用WGS 84 标准GPS 坐标，取自便携式装置中的GPS 定位模块。半正矢公式hav（）的具体计算过程见公式（3）。

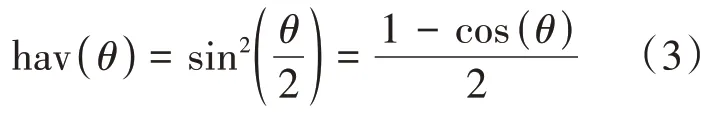
将公式（3）带入公式（2）第二个等号右边式子，得到公式（4）。

反半正矢函数的计算公式如公式（5）所示。

将公式（4）和公式（5）联立，得出距离的计算公式如下。

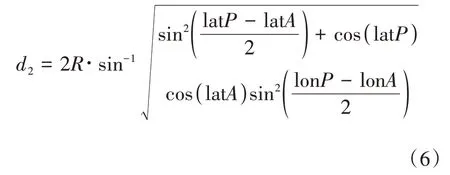
3 两种传统搜索算法

本文采用的传统搜索算法主要通过计算测试点与内置数据集各点的距离，选择数值最小的点作为输出结果。为了加快搜索速度，将经过Euclidean 或Haversine 公式计算后的距离集合进行排序，比较大小时采用传统的二分法进行搜索。详细步骤如下：

（1）算法初始化，将测试数据与内置数据集读入内存；

（2）利用Euclidean 或Haversine 公式计算内置数据集各点与测试数据间的距离，得到距离集合并排序；

（3）采用二分法搜索距离最小的点；

（4）结果返回对应内置数据集，输出地址字符串；

（5）算法结束。

应用5级行政区划数据进行测试。为排除计算过程中的随机影响，每次重复运行100次，取平均计算结果作为记录值。表3 中，传统1 和传统2 分别对应Euclidean 和Haversine 计算公式。传统1 代表采用Euclidean 公式计算单次运行时间，传统2 代表采用Haversine 公式计算方法单次运行时间。

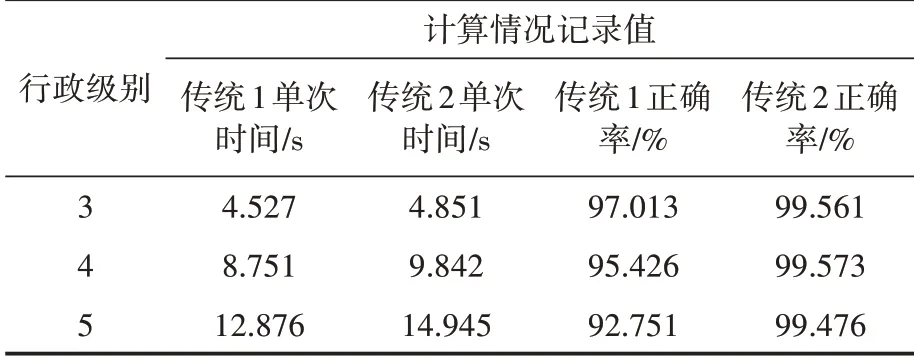
表3 传统算法在不同行政级别数据集情况下的计算情况

从表3可以看出，整体来看，随着内置数据集的增大，两种传统算法的单次计算运行时间逐渐增长。分别来看，采用Euclidean 公式的执行时间稍短，但是正确率低于采用Haversine 公式的传统2 算法。经手动排查后，发现传统1 算法判断失误的测试点与相邻最近的内置数据集点间距离较远，欧拉直线距离与球体表面的圆弧距离相对误差较大。总的来说，采用传统算法执行效率比较低，单个测试点的查询时间在4秒钟以上，因此在多数场景应用中是无法满足时效要求的。鉴于采用Haversine 公式的正确率较高，故选其作为下文的对照组算法。

4 K-d树算法的实现

k-d 树，即k-dimensional tree，常用作空间划分及近邻搜索算法，是二叉空间划分树的一个特例。通常，对于维度为、数据点数为N 的数据集，k-d 树适用于≫2的情形。以采用3级行政区划做内置测试集为例，维度=2，数据点数=3256，满足3256≫4 的应用条件。k-d 树算法可以分为两部分，一是为构建k-d 树本身这种数据结构而建立的算法，即如何把包含大量数据的内置数据集构建成一棵k-d 树；二是如何在建立的k-d 树上进行最邻近查找的算法，即查找k-d树上距离测试数据最近的节点。

构建内测数据集经纬度的k-d 树算法简述如下：循环依序取数据点的经纬度数据作为切分维度，分别取数据点在该维度的经纬度中值作为切分超平面，将中值左、右侧的数据点分别挂在其左子树和右子树。递归处理其子树，直至所有数据点挂载完毕。下面以3级行政区划数据集中的甲～庚共7个数据点为例，只保留其1级行政区划名称及经纬度数据；目标数据点是地处河北省石家庄市桥西区的新百广场商业综合体。具体数据见表4。

表4 简化k-d树算法所需数据点

具体步骤如下：

（1）构建根节点时切分维度为纬度，上述7个数据点按纬度从小到大进行排序，取中值乙点天津（39.14393，117.21081）为根节点；

（2）石家庄、邯郸、邢台三点在根节点的左半子树，北京、唐山、秦皇岛三点在根节点的右半子树；

（3）构建根节点的左子树时，切分维度为经度，中值点邢台（37.06953，114.52048）作为分割平面，邯郸为左子叶、石家庄为右子叶；

（4）根节点的右子树构建方法如上。

至此，k-d 树构建完成，如图2 所示。图中，每个数据点上的“经-N”或“纬-N”代表划分树或子叶时，以本点的经纬度作为切分维度的划分标准。

图2 7个数据点k-d树的构建示意图

上述构建过程结合图3，可以看出，构建一个k-d 树即是将一个二维平面逐步划分的过程。分割所用的超平面即是各个数据点的某一维度值。图3背景中的各条实线，即为分割所用的超平面，为方便辨识，经度线用粗实线标注，纬度线用细实线标注。

图3 k-d树搜索算法的“回溯”计算示意图

k-d树的搜素算法步骤如下：

（1）首先对k-d 树做深度遍历，取出距离最近的点，以图4标注的①→②→③为确定的搜索方向；

（2）为了明确丙叶子节点是否为真正的最邻近点，还需要进行“回溯”操作：具体为算法沿搜索路径反向查找是否有距离查询点更近的数据点；在图4 中，即为反向从③→④→⑤的过程；

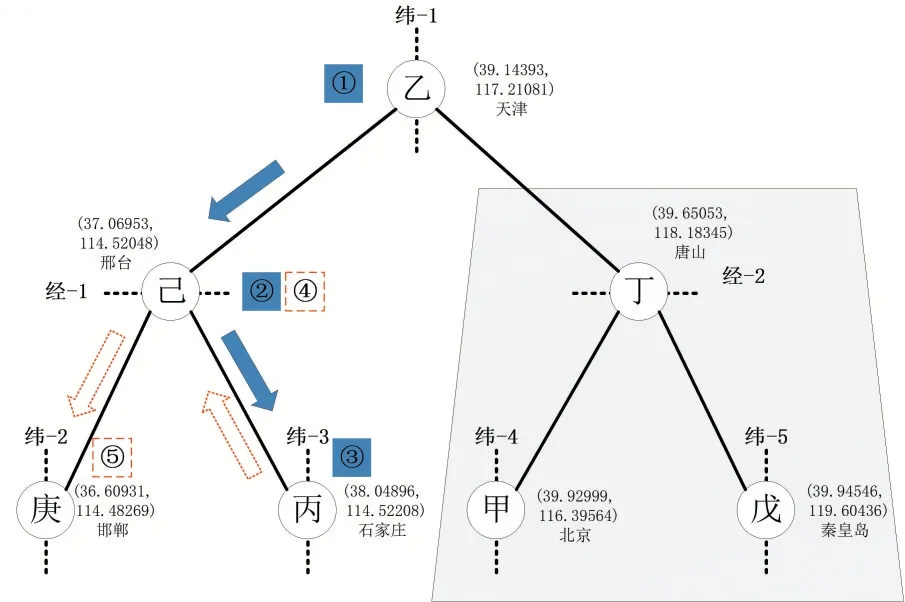
图4 k-d树搜索算法的实现

（3）“回溯”算法实现由图3 所示，图中的左下角实心五角星为需要查询的目标地址。图3中的“经-1/纬-3”分别为在丙点按经度、在己点按纬度做分割用的两个超平面。计算目标地址与丙点间的距离，以目标地址为圆心，距离为半径做圆。可以看到，圆与丙点的上一节点（己点）所确定的“经-1”存在交点，说明己点所在的左半树需要被“回溯”计算，完成过程④。而唐山所处的整棵树的右半树，由于未与所做出的圆出现交点，故不需要被计算，图中用阴影覆盖以示区分。同理，二级回溯完成过程⑤。

（4）再比较己点、庚点和两点与目标点的具体距离，选出距离目标点最短的那个点，k-d树搜索算法完成。得出丙点是所查询地址的结论，即新百广场位置在石家庄。

（5）以上步骤演示的是需要进行“回溯”计算的情况。如图3中右下方，虚线圆圈中的实心三角为目标点的另外一种情况：当目标点与最近的内置数据点之间所作的圆，与其他超平面无交点时，则不必进行“回溯”操作。

应用上述的k-d 树算法编写测试程序，在其他软硬件测试条件与第4节一致的情况下，得到的测试结果如图5所示。图中横坐标刻度值为log 值，测试集数量在第一个测试点为296 个，随后每次增加10 倍，最后一个测试点的数量达到2.96*10个。折线图每个点附近的数值代表其算法执行时间。

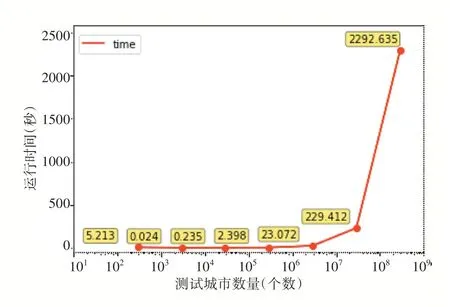
图5 k-d树算法在5级行政区划下的计算结果

在第一个测试点，同样输入296个测试数据和5 级行政数据的情况下，k-d 树算法的执行时间仅为5.213 秒，换算成单点计算时间为0.017611 秒，相比于表2 中的传统2 算法4.851秒，算法效率提升了274.45 倍。同时，算法正确率达到100%。

5 结语

针对离线逆地理编码算法的研究，本文首先采用两种传统搜索算法进行测试，并对由半正矢公式进行球面距离计算的过程进行详细推导，通过计算得到了传统算法时效性低的结论。然后，通过搭建7个数据点的简单k-d 树模型与算法演示，阐述了k-d 树算法的基本原理与计算步骤。测试结果表明k-d 树算法能够大幅提高计算效率和准确率。