网络异常检测技术的研究与应用

顾惠超

（安阳师范学院，河南 安阳 455000）

0 引言

计算机网络异常检测技术是入侵检测研究的重要内容，与基于规则（签名）的入侵检测相比，其最大的优点是能够检测到未知的脆弱性和零攻击（Zero-Day Attack）。一般的异常检测技术主要包括基于统计方法的异常检测和基于专家知识的异常检测。但是，由于误报率高、攻击范围不全面、检测效率不满足高速网络的实时检测需求等，这些异常检测技术在实际环境中没有被大规模应用。

因而，基于机器学习的异常检测技术逐渐成为研究的热点。通过机器学习的方法，首先比较待检测的数据与正常数据的轮廓，当达到一定偏移量时会发生检测到异常，再进行报警，这就是基于正常特征的数据用于检测网络异常的方法。当前，用于检测网络攻击行为的最佳数据源是网络数据流，因此，基于网络的异常侵入检测系统可以研究和应用最广泛的检测技术。

1 基于支持向量机分类的网络异常检测技术

分类器是通过对一组带标签的样本进行学习而产生的模型，之后用这个模型对测试样本分类。用分类器检测网络异常，一般分成两个阶段：

（1）训练阶段，在该阶段，分类器对训练集样本学习分类；

（2）测试阶段，在该阶段，用训练好的分类模型对测试集样本分类。

支持向量机（Support Vector Machine，SVM）在处理非线性分类问题上的操作是，首先把输入空间映射到高维的特征空间，然后用大间隔因子在高维特征空间中寻找最大间隔超平面。由于高维特征空间的超平面与输入空间中的非线性分类面相对应，因此，支持向量机的优化过程是通过线性核、多项式核和高斯核等核函数把高维特征空间中的内积运算转化为原始空间中核函数的运算。

首先假设，在给定的特征空间中，一个SVM 分类器可以对正常类和异常类进行有效区别。几种常用的基于SVM 的网络异常分类检测技术原理如下。

1.1 核支持向量机模型

核支持向量机模型（Kernelized SVM）利用不同的核函数，可使SVM 具备非线性分类和回归能力[1]。SVM 技术需要结合使用不同核函数对网络异常进行分类，其中几种常用的核函数如下所示。

高斯核函数：

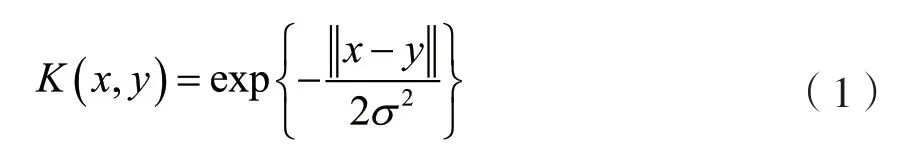
式中：y是核函数中心，σ是函数的宽度参数，控制函数的径向作用范围。

多项式核函数：

式中：参数d是正整数，表示最高项次数，a是正实数，c是非负实数。

线性核函数：

1.2 单类支持向量机模型

如果在数据集中出现未标记的训练数据集，通常采用（One-Class Support Vector Machine，One-Class SVM）[2]的方法来对网络异常数据进行检测分类。其表达式如式（4）、式（5）所示。

式中：函数Φ(xi)表示训练数据集合X映射到点积空间F时的特征图谱，此时Φ(x)可以用一些简单的核函数表示，如高斯核函数等。当ξi松弛变量被目标函数惩罚时，w和ρ是该目标函数中针对该问题而设置的初始参数。此时，正则项||w||取最小值时，f(x)=(w·Φ(xi))≥ρ-ξi对训练集中的样本x正相关。v为异常值的分数设置了一个上限（训练数据集里面被认为是异常的）。l是一个正整数，表示训练数据集的数目。

作为无监督学习方法，该方法被广泛地应用于检测无标记的数据。但是就目前的检测准确率而言，相比于有监督的学习方法，该方法还需要进一步发展改进来提高检查精度。

1.3 SVM 与其它机器学习技术结合

基于SVM 的异常检测方法非常适合小样本检测，原因是其异常检测速度快、效率高、检测精度高，因此成为当前的研究热点。如今，学术界经常用将SVM 与其他算法结合的方法来检测异常。利用SVM 和蚁群算法相结合，并将数据集从高维通过特征选取方法降为低维（如将41 维输入向量降低为19 维），实现了检测精度的提高[3]。使用SVM来进行分类，使用动态增长的自组织树来进行聚类并确定边界数据的方法来解决大样本数据训练速度过慢的问题[4]，将SVM 与决策树（Decision Tree，DT）和模拟退火算法（Simulated Annealing，SA）结合来解决维度灾害问题[5]。

基于SVM 检测技术的方法通常需要比较干净的数据，而实际流量数据通常包含了大量的噪声数据，因此，检测结果的误报率高，检测精度不足。由于有监督的机器学习检测方法需要人工标记大量数据，面临大量的困难，基于半监督或无监督的SVM 检测技术逐渐引起了学者重视。

2 基于神经网络的网络异常检测技术

2.1 自组织映射神经网络

利用自组织映射神经网络（Self-Organizing Map，SOM），可以使数据成为无监视学习集群。SOM 是“无监督学习”模型中的一种。ANN（MLP）模型与SOM 模型在结构上相似，不同的是，SOM可以将高维的Input 数据显示在低次元空间，也可以应用于数据可视化和集群。

SOM刚开始被用于误用检测（Misuse Detection）的方法上。从本质来看，其中的神经网络只包含了两个层级，一个是隐藏层，另外一个是输入层[6]。隐藏层中的每一个节点对应的是需要进行集合的类，具体的训练选择的方法是冲突学习。对于其中每一个输入事例进行分析可以发现，每一个隐藏层都有对应的匹配节点，这个节点属于活动节点。其中“winning neuron”可以针对已经激活的每一个节点参数进行修改，使用的方法是随机梯度下降，另外这些节点附近的点也会根据与活动节点之间的距离大小来改变和调整对应的数据。

SOM 的隐藏层的节点之间存在拓扑关系。需要确定这个关系，将隐藏节点连成一条线，就形成了一维模型；二维拓扑关系是平面，其二维拓扑关系如图1 所示。

图1 SOM 结构图

隐藏层的拓扑关系允许SOM 模型将任意维度输入离散到一维或二维（更高维度的非一般）离散空间。Cmaptation layer 中的节点与Input layer 的节点完全连接。其计算过程如下。

初始化：所有的节点都将自身的参数数据进行初始化设置，每一个节点的参数个数将会与Input数据的维度保持一致。

所有的输入数据都可以找到对应的节点来进行匹配。如果在输入时假定X={xi,i=1,2,…,D}为D维，则判别函数可以为输入向量X和权重向量wi,j的欧几里德距离：

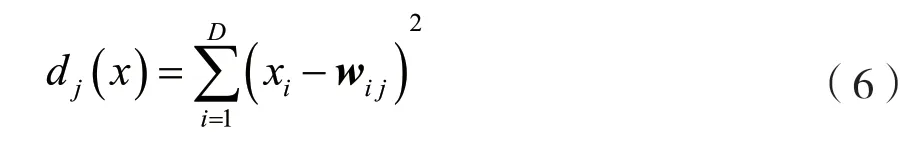
如果其中存在活动节点I(x)，那么就应该进一步针对其附近的节点进行更新。在所有神经元网格上，Sij表示任意两个神经元i和j的横向距离。这个距离数据直接决定了活动节点的分配更新权重。

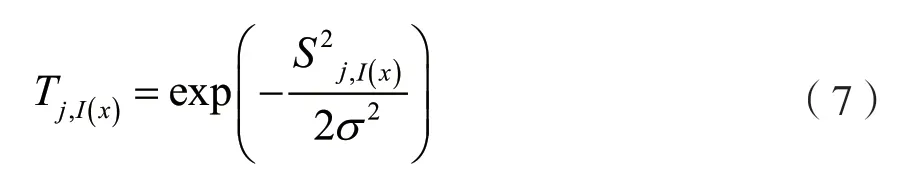
在SOM 中，σ是一个特殊的特征，表示邻域大小，其随着迭代次数而减小。

下一步需要对节点参数进行更新，具体的操作是基于梯度下降法进行的：

进行迭代，直到收敛。式（8）中：公式η(t)=η0exp(-t/τn)表示一个依赖次数t的学习速率。还需要在初始状态开始，选择合适的初始参数η0和τn。

2.2 自生长分层自组织映射神经网络

随着研究的深入，SOM 的弊端逐渐表现出来：必须预先确定网络大小和架构，固定网格的投影不能直观地表示数据中的分级关系。基于以上SOM算法的缺点，有学者提出了自生长分层自组织映射神经网络（Growing Hierarchy SOM，GHSOM）。该网络将SOM 分为多层网络结构，并基于输入数据进行结构的自适应拟合，其网络结构如图2 所示。

图2 GHSOM 算法结构示意图

2.3 GHSOM 与其他机器学习检测算法结合

为了进一步提高检测精度，不同的研究人员将GHSOM 与其他检测方法或检测思想结合起来使用，如：

（1）GHSOM 与K-means 结合，提出一种半监督的检测方法来提高精度[7]；

（2）GHSOM 与SVM 结合，使用GHSOM 来对网络流量进行聚类及相应的可视化，基于GHSOM的Label 标签，再使用SVM 来进一步进行异常行为分类[8]；

（3）GHSOM 与CSFS（Classifier-specific feature selection，CSFS）结合，该论文的实验结果显示减少了GHSOM 生成的层数，并提高了检测效率与精度[9]。

3 基于聚类的网络异常检测技术

3.1 基于欧式距离的聚类算法

基于欧式距离的聚类（K-means）算法属于硬聚类算法，它也是典型的目标函数聚类方法之一，具体是以模型为基础实现的。其中还需要使用到目的函数来进行优化，具体的优化过程必须测量数据点到圆形之间的距离大小。使用其中的计算函数极值方法，就可以分析得到迭代计算过程中的调整规则。

德国图宾根大学的GERHARD MUNZ 等在入侵检测中首次引入该算法，采用了流量的统计数据作为特征，在判断时将分类器（Classification）和异常点检测（Outlier Detection）结合进行检测，如图3所示。

图3 K-means 入侵检测示意图

步骤如下所示：

（1）随机在图中取K个种子点；

（2）对于图中的所有点，确定到K种点的距离，并且当Pi最接近种子点Si时，Pi属于Si类；

（3）确定组的平均值，并将新的种子点作为类的中心；

（4）重复第（2）步和第（3）步，直到种子点未移动。

YU G 等提出了Y-means 聚类方法用于异常检测，该方法基于K-means，克服了K-means 方法对集群的依赖等问题。

RANJAN R 等提出了K-Medios 算法，计算集群中每个样本点距离的绝对误差（K-Manas 是集群中所有点的平均值）最小的点，作为新的中心点。

步骤如下所示：

（1）随机在图中取K个种子点；

（2）对于图中的所有点确定到K种点的距离，并且当Pi最接近种子点Si时，Pi属于Si类；

（3）计算集群中每个样本点距离的绝对误差（K-means 是集群中所有点的平均值）最小的点，作为新的中心点；

（4）重复第（2）步和第（3）步，直到种子点未移动。

K-SMedios 方法的优点是对噪声不敏感，并且远离组的点对分割的结果偏差不太大，并且少数数据不产生大的影响。算法使相异的综合最小化，所得簇相当紧凑，簇与簇之间分隔明显。缺点是它是对K-means的改进，但由于是由中心点选择的方案，所以算法的时间复杂度也比K-means 上升，计算量更大，一般只适合中小数据量。

3.2 K-近邻算法

K-近邻（K-Nearest Neighboors，KNN）算法从训练集中发现最接近新数据的k条记录，并根据它们的主要分类确定新数据的类别。

LIN W C，KE S W，TSAI C F 等在入侵检测中引入KNN 算法，结合聚类算法的中心点来构造新的特征进行分类。

算法步骤如下：

（1）训练数据集聚类，聚类中心点C={Cu1,Cu2,…,Cum}；

（2）找到每个数据点的最近邻；

（3）针对步骤（1）和步骤（2）的结果构建新特征，已知数据点集合A=(a1,a2,a3,…,an) 和B=(b1,b2,b3,…,bn)，则可以用以下公式求A，B数据点集合的欧式距离。

基于以上公式，可进一步计算出数据点集合D和中心点C的距离和数据点集合D与最近邻点集合N的距离。

（4）针对新的特征（一维）进行k-NN 算法分类，算法框架如图4～图6 所示。

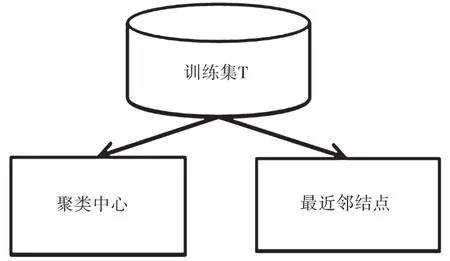
图4 提取聚类中心和最近临近点

图5 形成新的数据集

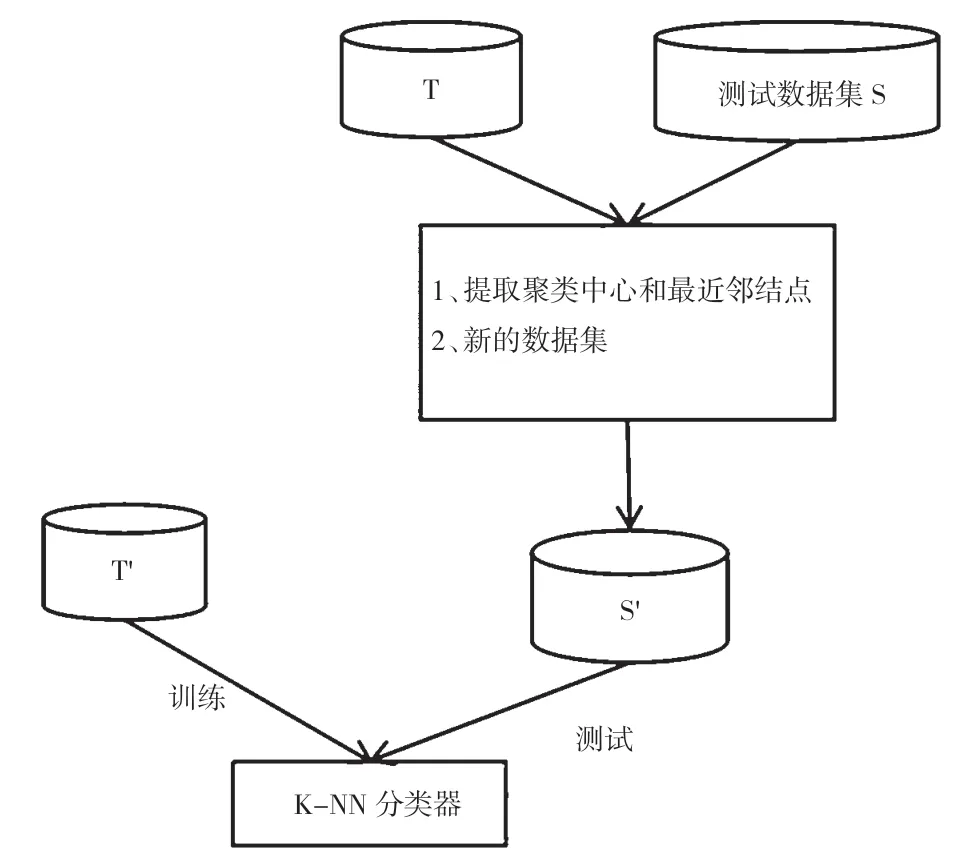
图6 形成K-NN 分类器

该算法的优势有：实现简单，重新训练的代价较低，按训练集的规模线性计算时间和空间。KNN法主要依赖于周边有限的邻近样本，算法适用于样本容量大的类域的自动分类，但是那些样本容量小的类域如果采用该算法，容易发生误差。

该算法的不足有：KNN 算法是散漫的学习方法，积极学习的算法非常快，类别评分不是规格化的，输出的可解释性不强，训练有更高的要求。如果样品不平衡，例如，一个类的样品容量大，而其他类的样品容量很小，当输入新样本时，与该样本的K个相邻的大容量类的样本占多数。另外，该算法的计算量较大，现在经常使用的解决方法是，事先将已知的样本点剪切，除去对分类没什么效果的样品，或者使用kd 树削减计算量。

4 结语

以上几种算法是检查网络异常的常用的、可靠的方法，能够检测出当前网络中存在的异常问题和安全问题。但是在检测过程中仍然存在一些问题，主要体现在以下几个方面。

（1）检测的快速实时性。针对高速网络动辄千兆、万兆带宽的实时流量，对检测模型及相关算法处理数据的实时性要求很高，同时在保证实时性的前提下，需要尽量降低误报率和漏报率。

（2）高误报率（False Positive）和高泄漏率（False Negative）。目前异常检测面临的问题主要是高误报率及高漏报率，使得异常检测的实际应用受到限制。安全分析员被淹没在大量的假报警中，而真正的报警又没有被检测出来。

（3）警报过滤（Alarm Filtering）。传统的异常检测通常认为恶意行为表现一定异常、而善意行为表现正常。在实际复杂的环境中，恶意行为通常通过伪装自己从而表现正常，而善意行为在特定条件下有时也会表现得异常。针对这部分可疑警报，需要被增强过滤或增强转发至二次检测，以提高检测精度。

（4）数据训练模型的自适应性。传统的训练模式通常采用离线训练、在线运行的方式。线下与线上环境的差异，以及线上环境的实时动态变化，导致检测效果不理想。更新训练通常在线进行，缺乏适应能力。

因此，综合这些问题，网络异常检测不再仅仅局限于方法的操作。一个形成体系的完整检测框架，是进一步需要研究的热点方向。