基于协同学的区域综合交通系统客运生成研究

周 凡 ，华雪东 ，谢文杰

（1.东南大学交通学院，江苏 南京 210096；2.东南大学江苏省城市智能交通重点实验室，江苏 南京 210096；3.东南大学现代城市交通技术江苏高校协同创新中心，江苏 南京 210096；4.中铁第四勘察设计院集团有限公司，湖北 武汉 430063）

引 言

作为城市交通规划的基础和交通需求预测的首要步骤，客运生成的精度直接影响了城市道路交通规划建设的合理性及科学性［1］。国内外交通领域专家和学者对客运生成预测进行了长期研究，产出大量研究成果，形成了一套相对完整的理论体系。常用的客运生成预测方法主要有增长率法、交叉分类法、函数法和回归分析法等。由于土地利用强度会对出行生成造成重要影响，曲同庆等［2］基于该认识，以各个交通小区之间的出行阻抗作为可达性指标，研究了交通可达性对出行生成的影响。近年来，综合交通网络基础设施日趋成熟，加之大数据技术迅速发展，交通需求分析的研究开始与深度学习、大数据分析理论等结合，逐渐诞生了一系列具有创造性的理论研究成果［3-5］。李雪琪［6］基于高德地图和百度地图爬取了POI数据，通过多源数据融合技术将两种来源的数据进行融合，并基于融合后的POI数据进行交通生成的预测。李帅等［7］通过电子警察系统得到大量卡口数据，建立了逐步回归分析模型，并通过与灰色预测模型的耦合实现对回归模型中人口、就业岗位等灰色变量的预测。

通过对已有研究的总结可以看出，当前的客运生成研究主要存在以下三方面不足待完善：一是区域层面的客运交通生成预测相对缺乏。现有的生成预测研究理论一般应用于城市交通需求预测，服务于城市交通规划，而综合交通方面的生成分析研究则聚焦于区域层面，区域与城市在规模、网络复杂程度、交通运输方式类型、交通系统影响要素等均存在较大差异，经典城市客运生成理论可能不完全适用于区域交通，因此需要针对综合交通特性展开特定客运生成分析。二是区域层面数据积累不足。综合交通系统理论的研究和实践起步较晚，对于区域交通的研究也较少，交通基础数据积累不足，导致可供分析用的数据体量受限，无法满足大数据分析、深度学习等新理论方法对数据的要求。三是交通生成的影响因素考虑不够全面。传统的交通生成预测方法主要是依据土地利用、社会经济发展水平、居民个人及家庭属性等指标来进行预测分析。对于交通需求的研究，主要考虑以交通影响因子作为自变量，交通需求作为因变量，建立映射关系求解，而实际的交通系统环境中，系统间各要素相互影响，互相作用，不能割裂系统展开研究，需要协同考虑，分析要素间的连锁效应。

事实上，区域综合交通系统是一个复杂开放的大系统，并隶属于社会经济体系，其运转受到社会经济系统中其他子系统的影响与制约，如城市形态、土地人口、土地开发、区域城镇的布局与城镇经济的发展［8］等。此外，在区域综合交通系统内部，其又是由包括公路、铁路、水运、航空等很多复杂子系统构成，各个子系统之间同样相互影响与制约。例如，如果公路客运价格下调，必然会对铁路、航空等其他客运产生影响，并可能导致其他客运方式的价格下调。

作为这样一个复杂开放系统，区域综合交通系统不断与外界环境进行物质、能源、信息等的交换；而区域综合交通系统内部的运输方式间，也同样进行着运输资源、运输能力与消耗的交换。这种区域综合交通系统的交互影响关系，恰好与经典的协同学理论非常相似：即，通过系统内各要素的协同作用，自发地形成具有一定结构的有序状态［9-11］。如若能够借助经典协同学理论，在相对较少的数据体量下，把握综合交通系统的协同作用机理，提升综合交通系统客运生成的分析精度，显然具有理论与实践层面的重要意义。

本文基于协同学理论，依托统计年鉴数据建立了精度更高的区域多方式客运系统协同竞争模型，对区域综合交通系统的客运生成进行预测研究，思路如下：在梳理经典协同学理论的基础上，提出区域综合交通系统的协同学分析原理，并针对区域综合交通系统的自演化发展过程，以及系统间的协同竞争关系，分别构建自演化模型与协同竞争模型，最后以江苏省的综合交通系统为案例，测试本文研究提出模型的生成预测效果。

1 协同理论

1.1 协同理论简介

协同学是研究不同事物之间的共性及其协同机理，同时结合了系统论、信息论、控制论、突变论等现代科学最新成果的一门新型综合性学科［9］。协同学认为客观世界存在各种各样的系统，这些系统看似完全不同，其实存在着很多的相似之处，各个系统之间相互影响、相互合作。企业系统就是一个典型的协同系统，企业系统是一个复杂开放的大系统，企业的运转需要各子系统之间协同发展，以产生整体涌现效应的运作机理与工作方式［12］，如图1所示。

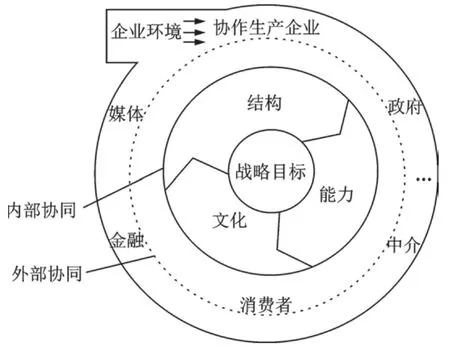
图1 企业战略协同机制［12］

协同理论通过类比对从无序到有序的现象建立了一整套数学模型和处理方案［13-14］，该理论已经广泛应用于很多领域，近些年来逐渐应用与交通领域。Miyamoto等［15］展开了交通运输系统与环境协同发展的研究。Olemskoi等［16］运用协同学理论分析交通流自组织现象。卞凤兰［17］基于协同学理论，分别建立了公路网规模与经济发展、交通需求、土地资源的适应性评价模型，经过模型分析发现公路网规模与经济发展、交通需求和土地资源之间均是互相影响、互为因果关系的。

1.2 区域综合交通系统的协同原理

区域综合交通系统的协同是系统内部各子系统之间的协同，简称系统协同。区域综合交通系统是由公路子系统、铁路子系统、航空子系统、水运子系统和管道子系统构成的一个复杂的大系统，各子系统在自组织演化的同时又相互影响，相互联系，促成区域交综合通系统的整体发展，即区域综合交通系统的协同是建立在各子系统相互独立、配合和整体发展同向的要求基础上的。因此，系统协同发展机理可以应用于区域综合交通系统的宏观调控。作为一个开放系统，区域综合交通系统与外界环境不断发生物质、信息和能量的互换，系统内部各载运方式都独立承担运输任务，自成一体地提供运输服务，满足客货物运输需求，同时每种载运方式也会受到其它载运方式的作用与影响，存在载运方式间的协同互动。

在初始阶段，公路子系统发展迅速，铁路子系统、航空子系统、水运子系统发展相对较慢。这一阶段中，上述各子系统各自为政、缺乏协调。随着交通技术的发展，运需、运价及运速等也在逐渐变化，各子系统之间的联系逐渐加强，方式之间竞争越来越大，各子系统之间分享市场的同时相互抢夺客源，形成了子系统之间的竞争。这一阶段中，子系统的客运生成量及旅客周转量在各子系统的发展和竞争的过程中起到主导作用，依照协同学原理，上述两个变量被称为慢弛豫参量［18］，即序参量。随着交通系统进一步发展与变化，各子系统无法单独承载交通需求，此时各子系统开始寻求合作，子系统之间的联系不断增强，协同作用日益强烈，子系统之间同时存在竞争与协同，区域综合交通系统进入稳定发展状态。

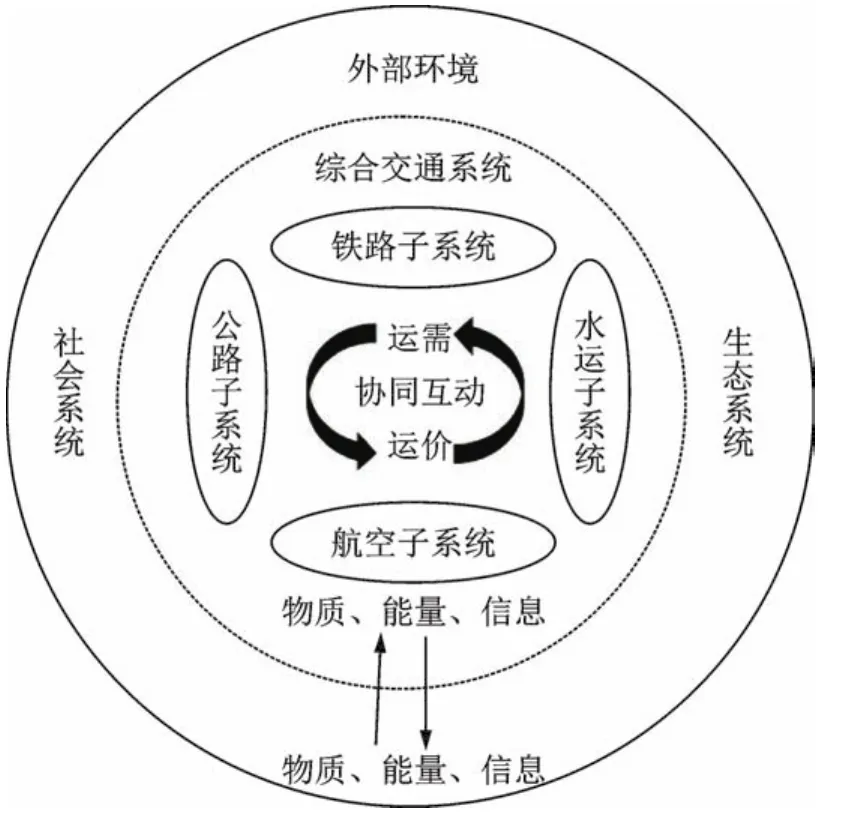
图2 区域综合交通系统的协同原理

2 区域多方式客运系统协同竞争模型

区域多方式客运系统指的是区域综合交通系统客运相关部分，其发展与区域综合交通系统内部各子系统的自演化发展及子系统间的协同作用密切相关。下面依次对区域多方式客运系统的自演化发展过程以及系统间的协同竞争进行建模分析。

2.1 自演化发展模型

自演化发展过程中，事物从无序的、混乱的状态向有序状态发展，或者是从有序状态发展成新的有序状态。区域综合交通系统的演化是公路、铁路、航空和水运等子系统在系统各组成部分间重新分布的结果。

自演化发展模型是描述区域综合交通系统内部各子系统序参量自组织演化发展的模型。设ci为旅客周转量；qi为客运生成量；的变化由自身的增长、自身增长的抑制、客运生成量对其的吸引三者共同作用决定［19］，即：

式中δi为旅客周转量的增长率；φi(ci)表示旅客周转量发展的自抑制项，即旅客周转量发展到一定的阶段发展速度会下降，为自身增长的抑制；φi(qi)表示客运生成量对旅客周转量的吸引作用。

客运生成量的增长会对旅客周转量具有吸引作用，旅客周转量又会反过来刺激客运生成量的增长，由此实现子系统的自演化发展。因此，对于客运生成量存在：

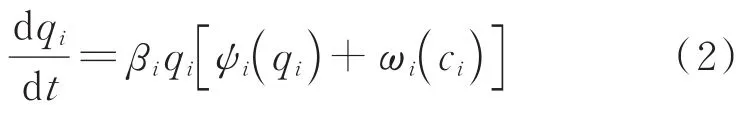
式中βi为客运生成量自身的增长率，ψi(qi)为客运生成量的自抑制项，ωi(qi)为旅客周转量对于客运生成量发展的刺激作用。

综上，子系统的自演化发展模型可以写成：

式中i=1，2，3，4，其中，1代表铁路，2代表公路，3代表航空，4代表水运。目前管道运输只用于货物运输，本文不予考虑。

2.2 协同竞争模型

铁路子系统、公路子系统、航空子系统和水运子系统之间互相竞争，这种竞争，不是“此长彼消”的“战争”，而是各方式客运系统在竞争中不断发展形成的良好的协同竞争。各方式在竞争综合交通客运生成总量分担率的过程中，不断提高各自旅客运输周转量，进一步促进各方式客运生成量的增长，各自客运生成量的增长又进一步刺激各方式旅客运输周转量的提高。竞争促进了发展，发展进一步优化了竞争。

协同竞争模型就是自演化发展模型上，引入协同竞争关系的修正模型。它同时考虑了各子系统序参量的自演化发展以及不同子系统之间的协同竞争。

假设铁路旅客运输能力受到其他系统参量对其协同竞争作用为U1（c2，c3，c4，q2，q3，q4），U1（c2，c3，c4，q2，q3，q4）即为铁路旅客运输能力的协同项，其他同理。铁路客运生成量受到其他系统参量对其的协同竞争作用为G1（c2，c3，c4，q2，q3，q4），公路旅客运输能力受到其他系统参量对其协同竞争作用为U2（c1，c3，c4，q1，q3，q4），公路客运生成量受到其他系统参量对其协同竞争作用为G2（c1，c3，c4，q1，q3，q4），航空旅客运输能力受到其他系统参量对其协同竞争作用为U3（c1，c2，c4，q1，q2，q4），航空客运生成量受到其他系统参量对其协同竞争作用为G3（c1，c2，c4，q1，q2，q4），水运旅客运输能力受到其他系统参量对其协同竞争作用为U4（c1，c2，c3，q1，q2，q3），水运客运生成量受到其他系统参量对其协同竞争作用为G4（c1，c2，c3，q1，q2，q3）。

因此同时考虑各方式客运系统自演化发展与系统之间协同作用，使用绝热消去原理［11］化简后的自相关项的分方式客运系统协同竞争模型为：

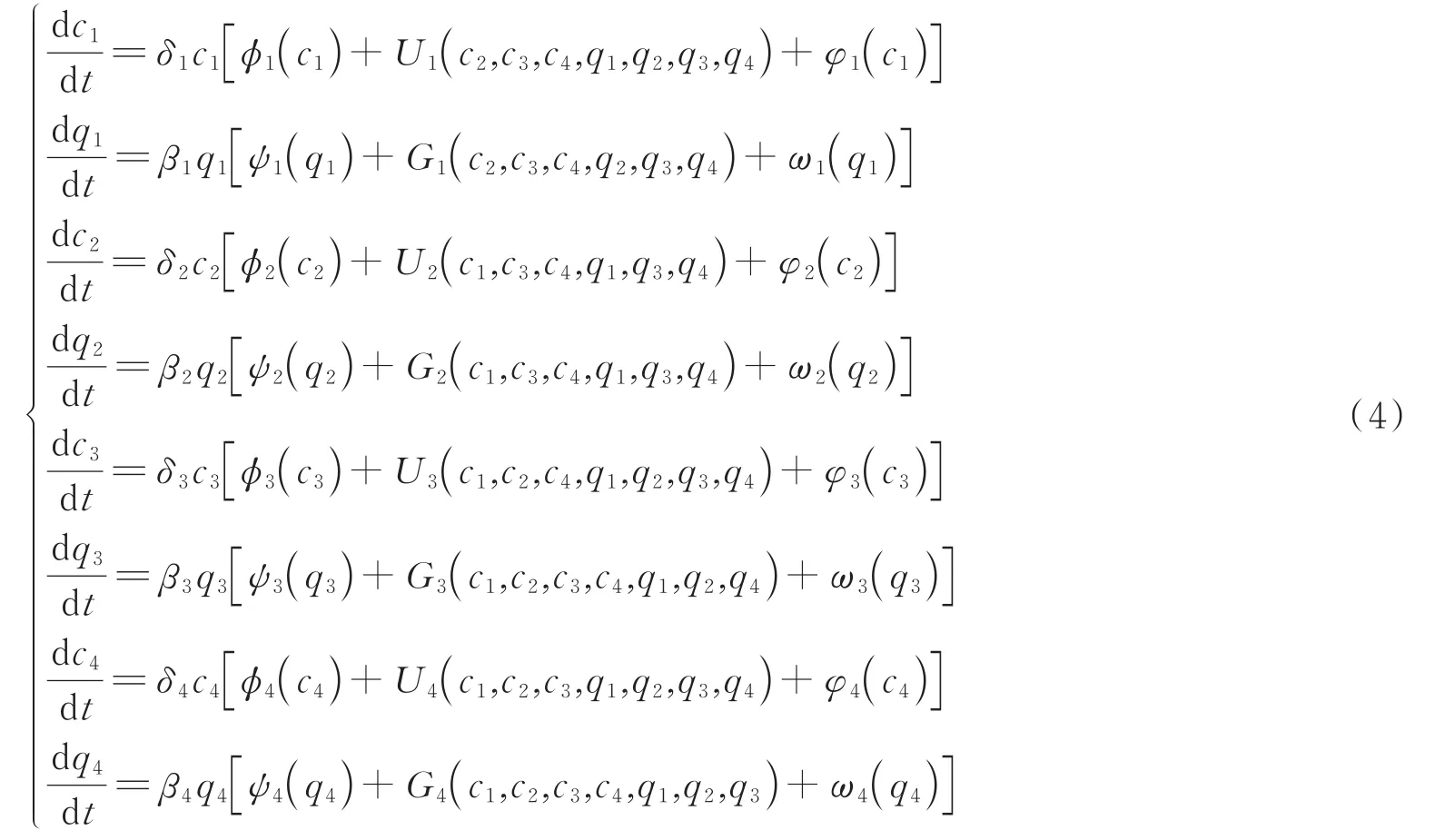
3 案例分析

作为国内第二经济强省，江苏省拥有完整的交通运输体系，故本文以江苏省综合交通系统为例，基于本文提出的区域多方式客运系统协同竞争模型对江苏省的公路客运生成量进行预测。表1是1990～2019年江苏省铁路客运生成量/旅客周转量与公路客运生成量/旅客周转量数据表（数据来源于《中国统计年鉴》［20］）。图3为1990～2019年江苏省公路客运生成量。从图中可以看出，1990～2012年江苏省的客运生成量总体上呈增长的趋势，由1990年的不到五亿增长到2012年的二十五亿，增长了四倍之多，但是在2013年江苏省公路生成量急剧缩减。查找资料后（https：//www.zhihu.com/question/37790547）得知，2013年由于统计口径调整，剔除公交车等大运量、短距离的公路运输，导致公路客运生成量暴跌。考虑到统计数据的一致性，本文仅使用1990～2012年的数据开展案例分析。其中，1990～2004年的数据用于协同竞争模型的标定，2005～2012年的数据用于对协同竞争模型预测结果的评价。

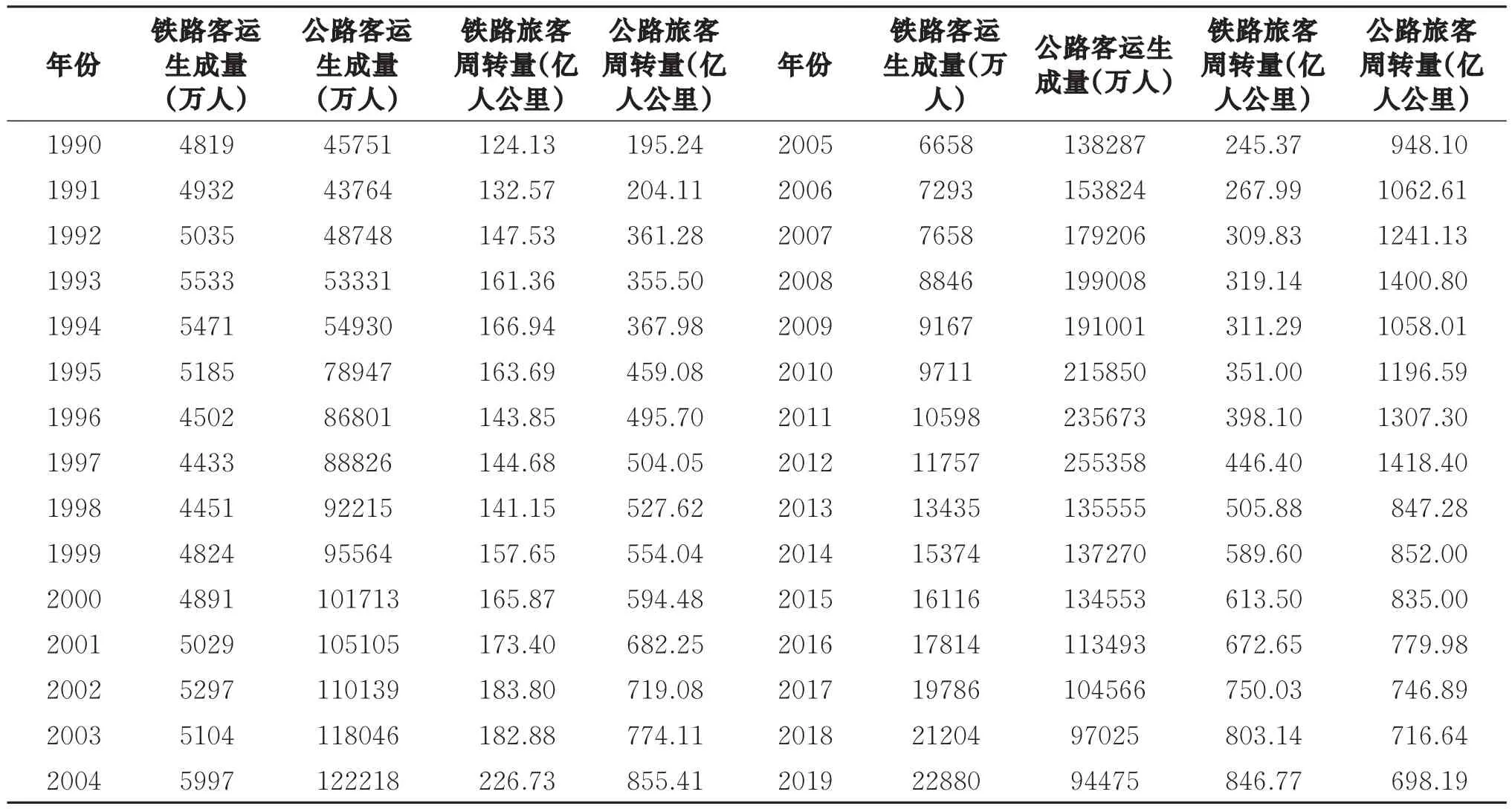
表1 1990-2019年江苏省铁路子系统和公路子系统相关序参量数据表

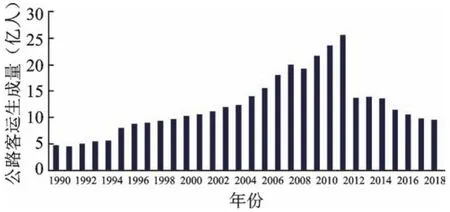
图3 1990～2019年江苏省公路客运生成量

1990～2012年江苏省客运总量为2974759万人，其中公路客运总量为2810404万人，占总量的94.5%，铁路客运总量为147160，占总量的4.9%，公路和铁路客运量占总客运量的99.4%（数据来源于《中国统计年鉴》［20］）。从历史数据容易看出，江苏省综合交通系统的公路、铁路承载了超过99%的区域交通出行需求。这一过程中，区域多方式间的协同发展与竞争在公路和铁路之间最为明显：相较于长距离的航空出行与服务旅游为主的水运出行，公路和铁路的优势运输距离重叠最大，两者间的竞争和协作最多。本文从简化分析建模的角度出发，在算例部分仅保留公路和铁路两种方式，开展区域交通系统协同竞争发展分析。

本节中，首先确定了江苏省公路/铁路客运生成量、公路/铁路旅客周转量的增长率，然后应用最小二乘法对协同竞争模型的系数进行标定与拟合分析；通过模型的迭代计算对2005～2012年的客运生成量和旅客周转量进行了预测，并将模型预测的结果和多项式预测的结果进行比较。

3.1 确定序参量增长率

图4为铁路及公路客运生成量增长率变化，从图中可以看出，1991～1997年公路客运生成量增长率起伏不定，尤其是1995年公路客运生成量急剧增加，达到了峰值，1997年之后增长较为平稳。图5为铁路及公路旅客周转量增长率变化。从图中可以看出，1993年公路旅客周转量大幅增加，增长率达到最大值，之后除了1995年和2001年增长率出现了一点小波动，整体增长比较平稳。为了减少宏观偶然事件及极端非稳定数据对未来预测的不利影响，更好地反映公路客运生成量、公路旅客周转量预测年的增长趋势，更准确地预测各序参量的发展变化，这里选取剔除特殊值后其他年份的平均增长率作为各序参量的增长率。因此，公路客运生成量、公路旅客周转量的增长率分别为：

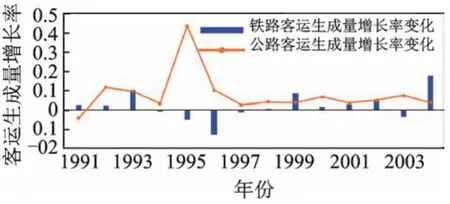
图4 铁路及公路客运生成量增长率变化

图5 铁路及公路旅客周转量增长率变化

3.2 模型形式的选择

2.2中建立的多方式客运协同竞争模型，可用于描述综合交通系统具有协同学基本特征的子系统及子系统之间的发展。模型中自抑制项、协同项、自相关项采用不同的函数形式，预测的结果也会有一定差异。

观察图3～5可以发现，除了极个别年份外，客运生成量和旅客周转量的增长率整体稳定，即客运生成量和旅客周转量当年的基数越大，其第二年其增量也越大。这种正相关的关系一般可以用多项式来表达。考虑到式（4）实际上为多项式，为了让构建的多方式客运协同竞争模型更具有一般性，本文选择了幂函数作为自抑制项、协同项、自相关项的函数形式，所构建的多方式客运协同竞争模型如下式所示：

3.3 参数标定

基于表1中1990～2004年的数据，使用MATLAB（R2019a）对上面多方式客运系统协同竞争模型的参数做非线性最小二乘拟合。得到标定后的多方式客运系统协同竞争模型如下：

将表1中1990～2004年的数据代入标定后的模型中，用迭代法对模型中得到的公路客运生成量及公路旅客周转量进行仿真，将两个参量的拟合值与真实值进行比较，可得基于多方式客运系统协同竞争模型的公路子系统序参量拟合分析图如6，7所示。

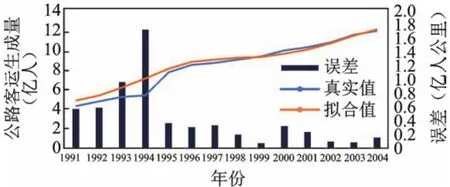
图6 公路客运生成量协同竞争拟合分析图

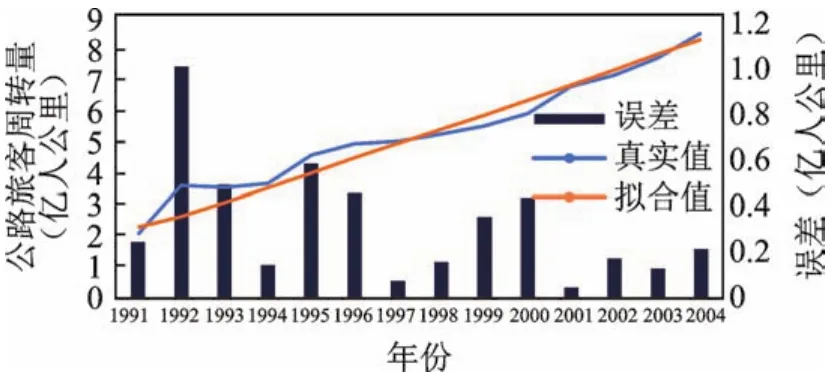
图7 公路旅客周转量协同竞争拟合分析图

由图6，7可见，公路客运生成量拟合曲线的确定系数为94.26%，平均绝对误差MAPE1=7.1%，拟合优度高，拟合误差小，准确描述了公路客运生成量的增长过程。公路旅客周转量拟合曲线的确定系数为95.08%，平均绝对误差MAPE2=7.36%，拟合优度及平均误差百分比均与公路客运生成量拟合曲线相近，同样具有较好的拟合效果。

3.4 预测结果及误差分析

本文对2005～2012年江苏省的公路客运生成量和公路旅客周转量的参量值进行预测。将2004年各参量数值作为初始数据带入标定后的协同竞争模型，得到2005年各参量预测值，然后将得到的2005年各参量预测值继续带入上述模型，求得2006年各参量预测值，重复以上步骤，在几次迭代后得到2012年各参量预测值。为验证模型预测效果，同时采用多项式模型进行了预测，将两种模型预测的结果进行比较如表2所示。其中，多项式预测采用具有代表性的三次样条方法。

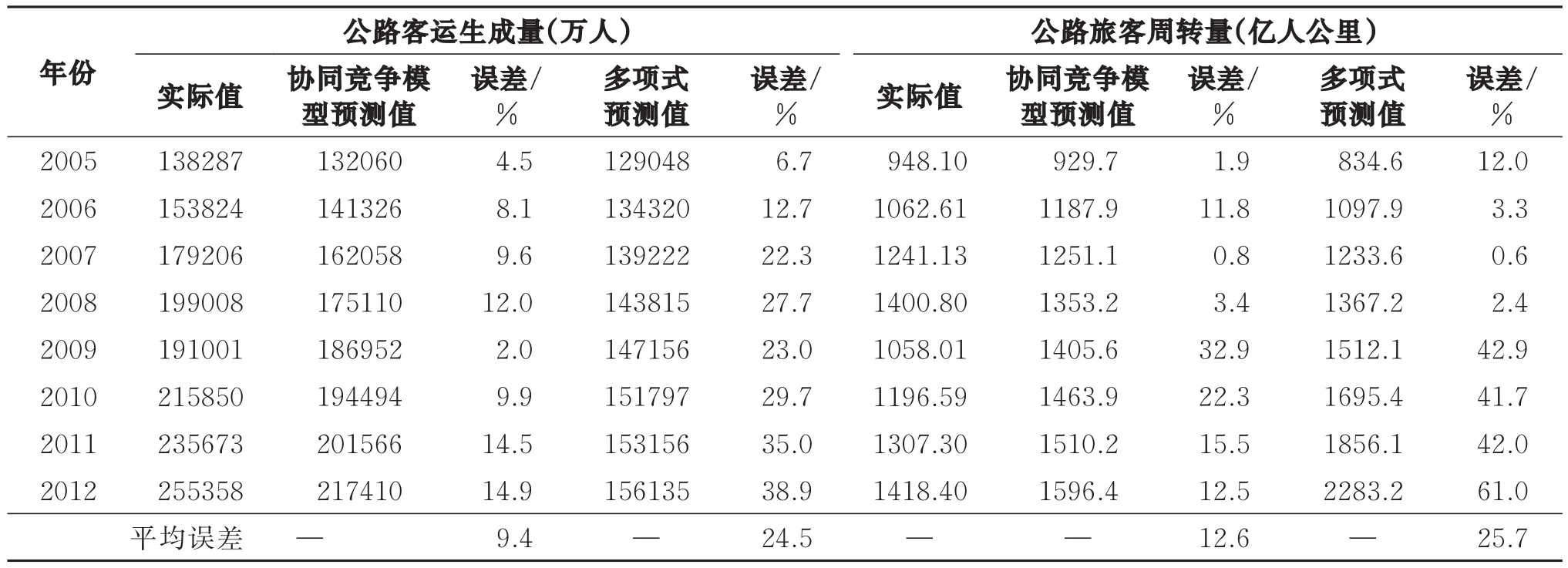
表2 两种模型预测值与真实值对比

从表2可以看出，区域多方式协同竞争模型对于公路客运生成量和公路旅客周转量的预测结果与真实值相差不大，平均误差分别为9.4%和12.6%，属于可接受范围。多项式预测的误差相比于协同竞争模型误差较大，且随着预测时间越来越长，误差越来越大，预测结果不太理想。由此可见协同竞争模型准确率较高，比常用的一些预测模型更适合于区域客运生成的预测。

4 总 结

1）针对传统区域客运生成预测模型无法表达交通系统间协同与竞争关系的问题，本文引入了经典协同学理论，提出了区域综合交通系统的协同原理，建立了区域多方式客运系统自演化发展模型与协同竞争模型，并通过江苏省公路的客运生成量与旅客周转量为例开展了案例分析，验证了本文模型的有效性。

2）案例分析的结果显示，区域多方式协同竞争模型可以高效与高精度的分析预测区域多方式客运系统生成量与周转量，预测结果更加准确：对于两者预测的平均误差为9.4%和12.6%，相比多项式模型预测的误差降低了63%和51%。

3）在本文案例分析的部分，多方式协同竞争模型中仅考虑了江苏省的公路、铁路两个主要的交通子系统，且模型的函数形式全部选择了幂函数。后续的研究需要进一步扩大研究的范围，测试与验证国内外更多的区域及交通系统，并测试包括对数函数、指数函数等更多的函数形式及其组合，以保证本文研究的普适性。