基于定数截尾样本的高档数控机床可靠性评估

许嘉莉，张权

基于定数截尾样本的高档数控机床可靠性评估

许嘉莉，张权＊

（齐齐哈尔大学 理学院，黑龙江 齐齐哈尔 161006）

在对某一高档数控机床进行可靠性评估时，当得到的数据为不完全的定数截尾样本，最好的建模方法就是威布尔分布，通过参数估计中的最好线性无偏估计得到威布尔模型的两参数值。并根据可靠性指标，失效率函数和平均无故障时间来对模型进行可靠性评估，从而得到该机床正处于偶然失效期，且该机床发生故障的频率稍高。

定数截尾样本；参数估计；失效率；平均无故障时间

每个产品在设计时，都需要先对它的寿命进行一定的考量，因为在应用到具体的环境或者场合时会有许多的变数，对于可修的大型机器在投入市场前进行可靠性评估更是重中之重。高档数控机床作为一种大型复杂的可修系统，历年来国内外研究学者对其进行可靠性评估的方法也层出不穷。以往的学者在对不完全数据进行选取时，通常采用定时截尾试验的方法，而对少样本数据的分析通常采用贝叶斯方法。宫雷等[1]采用定时截尾试验获得数据，通过Bayes方法对数控机床进行可靠性分析。Abu-Zinadah[2]对寿命问题的定时截尾样本数据进行了寿命竞争风险分析。李晨光等[3]为五轴联动数控机床引入多层贝叶斯进行建模，解决了先验参数的选择问题。龙沁怡等[4]在处理定时双截尾样本时，证明了EM算法具有良好的收敛性。本文采取定数截尾的寿命试验的方法，得到少样本数据，并采用威布尔分布进行可靠性建模，通过最好线性无偏估计对两参数值进行参数估计，最后根据失效率函数和平均无故障时间对数控机床进行可靠性评估。

1 威布尔分布

首先建立威布尔模型。对于数控机床这种可修性产品，其寿命分布基本服从威布尔分布。设某数控机床的故障时间服从威布尔分布[5]，则其寿命密度函数公式和分布函数公式为

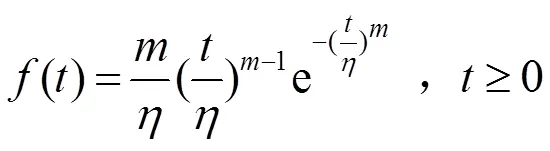
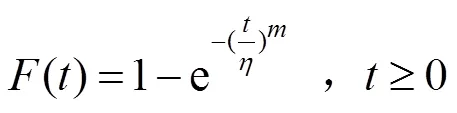
2 参数估计

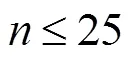
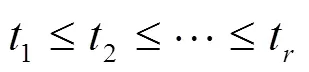
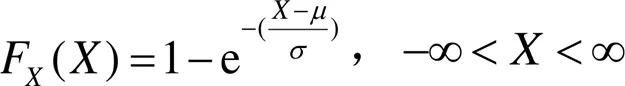
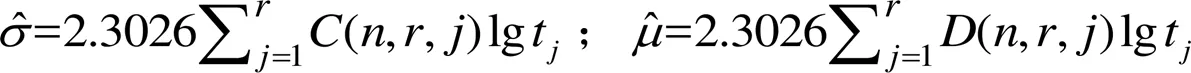
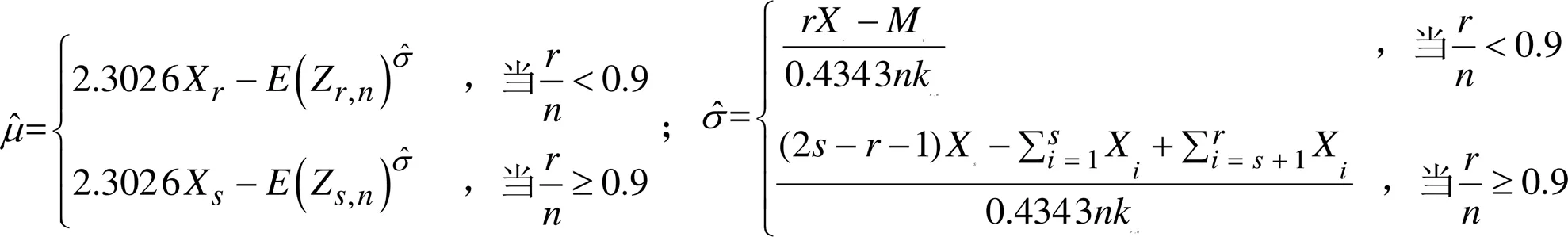
通过极值分布计算威布尔分布形参和尺参的公式为

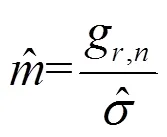
3 数控机床的寿命评估

数控机床寿命是指其从开始工作到发生故障前的一段时间。理论上所有产品都需要做寿命评估。故障率函数即规定时间和条件时，机床丧失规定的功能的概率[6]。通过故障率函数对机床寿命进行评估，故障率函数公式如下：

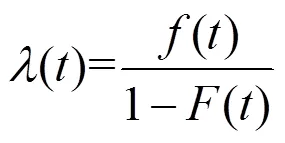
参考典型的浴盆曲线，绘制相应的故障率函数曲线。进一步判断该机床当前所处的失效期，以达到寿命评估的目的。

4 可靠性指标的状态评估

可靠性即规定使用条件和时间时，数控机床完成规定功能的能力。在这里，为了使状态评估结果数值化，用可靠性的指标之一：平均故障间隔时间（MTBF），来评估数控机床的可靠状态，公式如下：

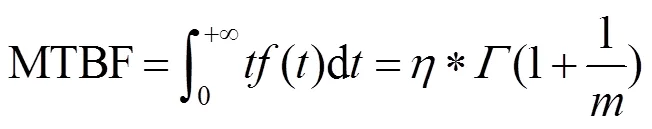
计算得到的平均故障间隔时间结果与查表得到的标准可靠性值作对比，以判断此机床所处的状态好坏。

5 实例分析

某数控机床故障时间服从威布尔分布[8]，对其故障时间进行定数截尾的寿命试验：从总体中抽取20个样本，试验到第15个样本失效时结束，记录故障时间数据如表1所示的第二列数据。

5.1 可靠性建模

已知样本数=20,故障数=15。由于样本数<25，在这里对威布尔两参数进行估计时，采用最好线性无偏估计的方法。线性无偏估计中各个系数的值，如表1所示。将相应系数直接代入式(4)和(6)，计算威布尔分布的形状参数和尺度参数：，。

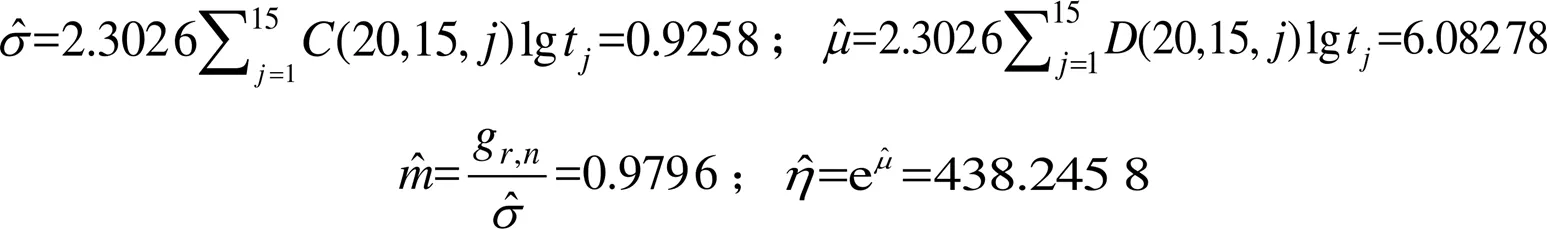
进而得到威布尔模型故障时间的密度函数和分布函数：

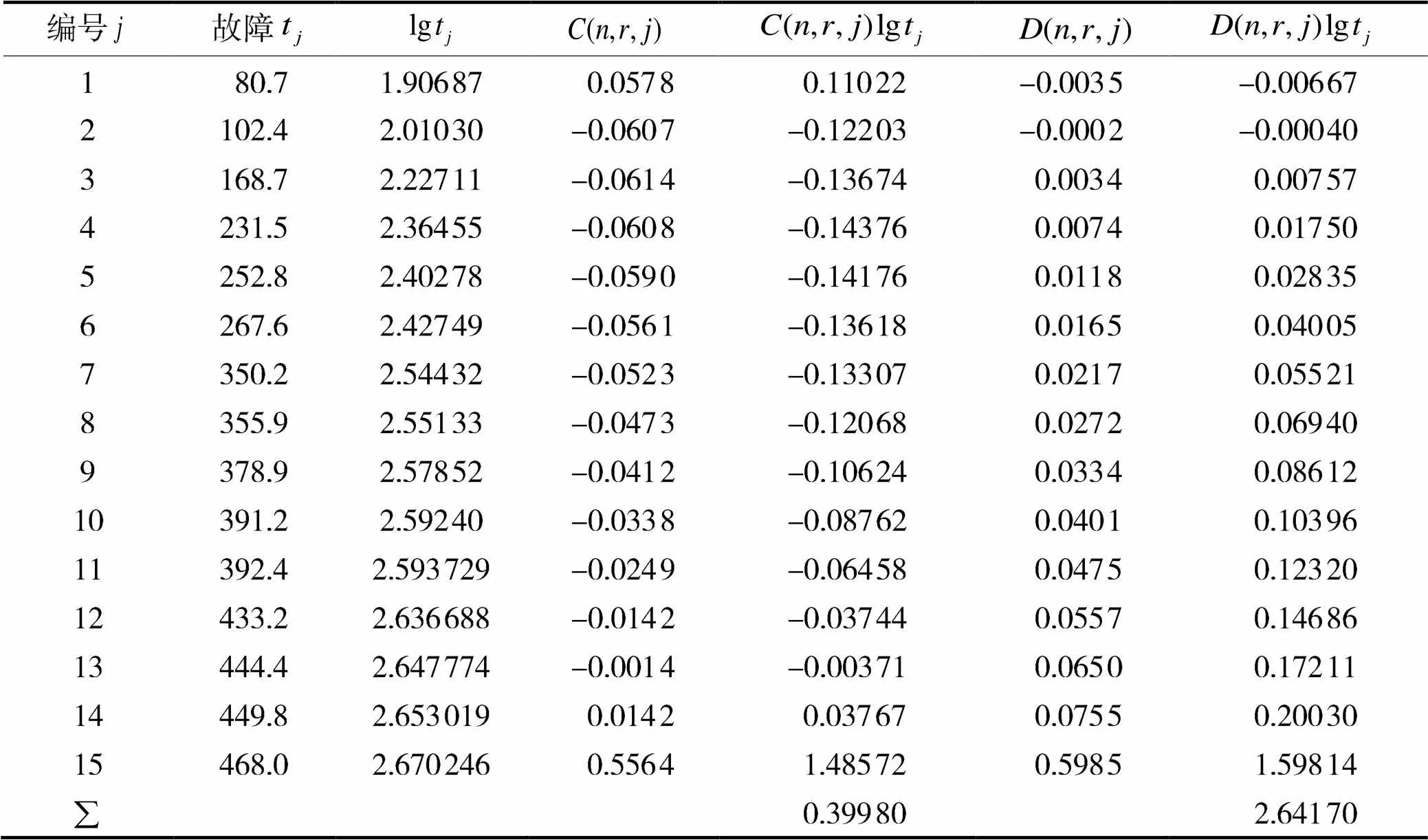
表1 故障时间及无偏估计系数值j

5.2 寿命评估

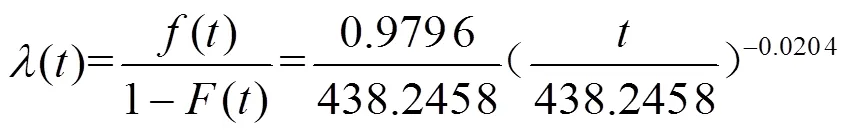
通过R语言绘制的故障函数的曲线如图1所示。

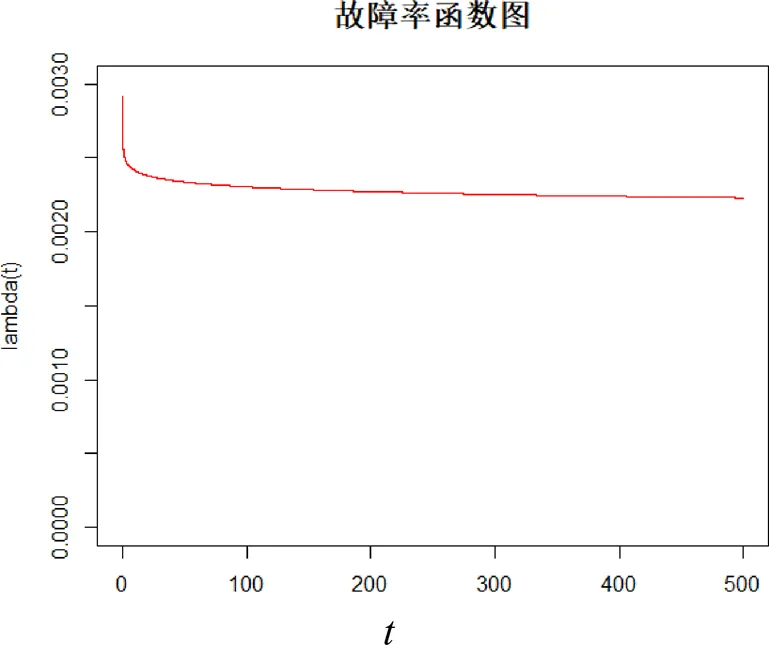
图1 故障曲线

与浴盆曲线相比，可知该机床处于早期故障期到偶然失效期的故障时期，偶然失效期是该机床最佳的工作阶段，即该机床已经生产使用多时。

5.3 状态评估

平均无故障时间计算结果如下：

已知标准靠性阈值MTBF的等级[9]如表2所示。

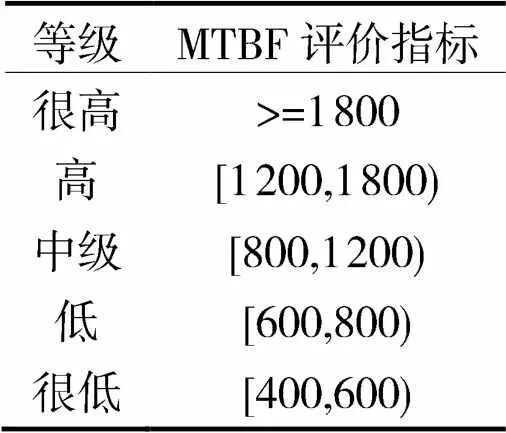
表2 标准MTBF阈值表

由表2可知，该数控机床的平均无故障时间值在[400, 600)之间，处于很低的水平，因此可以判断该机床在工作时发生故障的频率稍高。

6 结论

本文对一高档数控机床采用定数截尾的寿命试验获得的少样本数据，对其进行可靠性分析评估，建立威布尔模型，通过最好线性无偏估计的方法得到两参数值，并且得到该数控机床此时处于偶然失效期的工作状态，虽然此时是该机床的最佳工作时期，但是其平均无故障时间却处于很低的水平，从而得到该机床的性能并不是很好。根据历来研究学者的启发，对于少样本数据进行估计还可以参考贝叶斯的方法，下一步我们将对此进行着重研究。

[1] 宫雷，许世蒙. 定时截尾样本下某型数控机床可靠性的Bayes分析[J]. 信息系统工程，2018(07): 84-85, 87.

[2] ABU-ZINADAH H H. Lifetime competing risks data from Lomax distribution in the presence of accelerates life-testing model with Type-I censoring[J]. Journal of Intelligent and Fuzzy Systems, 2020, 38(3): 2873-2883.

[3] 李晨光，王红军，李连玉，等. 高档数控装备多层贝叶斯可靠性评估模型研究[J]. 组合机床与自动化加工技术，2020(04): 79-82, 87.

[4] 龙沁怡，唐俊. Ⅰ型双删失样本下Lomax分布形状参数的估计[J]. 云南民族大学学报（自然科学版），2018, 27(05): 408-412.

[5] 曹晋华，程侃. 可靠性数学引论[M]. 北京：高等教育出版社，2006: 15-17.

[6] 杜盼. 基于威布尔分布的数控机床可靠性评估方案[J]. 科技视界，2015(08): 118, 152.

[7] 梁米，李云飞. 双参数指数分布异常数据的检验[J]. 西华师范大学学报（自然科学版），2021(7): 1-3.

[8] 杜盼. 基于参数分布面向数控机床的威布尔分布期望的研究[D]. 天津：天津职业技术师范大学，2014: 24-26.

[9] 倪文凯，朴成道. 国外高档数控车床的可靠性综合评价[J]. 机床与液压，2016, 44(01): 198-201.

Evaluation of the reliability of high-grade CNC machine tool based on Type II censored sample

XU Jia-li，ZHANG Quan＊

(College of Science, Qiqihar University, Heilongjiang Qiqihar 161000, China)

In the reliability evaluation of a high-grade CNC machine tool, the best modeling method is Weibull distribution, and the data we get are incomplete Type II censored samples. The two parameter values of Weibull model are obtained by BLUE in parameter estimation. And according to the reliability index: failure rate function and MTBF to evaluate the reliability of the model, so that the machine tool is in the accidental failure period, and the frequency of the machine tool failure is slightly higher.

Type II censored sample；parameter estimation；failure rate；MTBF

2021-09-23

黑龙江省教育厅项目（135509127）

许嘉莉（1996-），女，河南周口人，硕士，主要从事应用统计研究，2794108675@qq.com。

张权（1978-），男，黑龙江齐齐哈尔人，副教授，博士，主要从事应用统计研究，zhangquan122400@163.com。

O213.9

A

1007-984X(2022)03-0091-04