复杂噪声条件下配电网鲁棒状态估计研究
2022-06-15施雅媛胡金峰孙帅
施雅媛 胡金峰 孙帅

摘 要:随着社会经济发展,配电网规模不断扩大,大量分布式电源的接入导致配电网的拓扑结构越来越复杂,进一步加大了对配电网稳定运行的分析难度。为了给电网调度提供准确实时的配电网运行状态,首先应具备足够数量的量测数据,然后通过实时量测数据进行计算分析,估算出全网的运行状态,这便是配电网状态估计的意义所在。然而,实时的量测数据往往受多方面因素影响,给状态估计带来了诸多复杂噪声的干扰。针对上述问题,提出了一种基于加權最小绝对值的配电网鲁棒状态估计方法,该方法考虑了多种噪声下的量测数据状况,提升了系统的鲁棒性,对配电网安全稳定运行分析有着非常重要的意义。
关键词:配电网;状态估计;鲁棒性
中图分类号:TM732 文献标志码:A 文章编号:1671-0797(2022)11-0016-03
DOI:10.19514/j.cnki.cn32-1628/tm.2022.11.005
0 引言
配电系统的快速发展也对其安全稳定运行带来了一定的挑战。近年来,随着配电系统的结构日趋复杂化,其监视系统也在稳步发展。但受限于量测误差和系统传输误差等因素,直接获取的量测数据往往存在着准确度较低的问题,同时为了降低成本,量测数据并不能直接反映配电系统的运行状态,而是需要通过状态估计进行分析,从而获得全网的精确运行状态数据[1]。状态估计以提高数据的精度为目标,能够筛除错误数据,并降低随机噪声的影响,对判断配电系统的运行状态有着非常重要的作用[2]。
为了进一步提升状态估计算法的精度,提高其应对多种复杂噪声情况的能力,已有相关研究提出了多种抗差状态估计、鲁棒状态估计方法。文献[3]针对预测—校正内点法加权最小绝对值状态估计可能发生校正方向指向错误方向的不足,提出了一种基于多预测—校正内点法的WLAV抗差状态估计算法,提高了算法的收敛速度及抗差能力。文献[4]基于已有电力系统的精确线性化量测方程,提出了一种基于加权最小绝对值的双线性抗差状态估计方法。文献[5]提出了一种抗差容积卡尔曼滤波算法,在不同量测噪声且量测量存在不良数据的复杂情况下仍具有较好的估计精度,并能消除不良数据带来的影响。随着配电系统的运行环境日趋复杂,传统的鲁棒状态估计算法需要面临更多复杂噪声情况,本文着重考虑了多重噪声条件,提出了一种改进鲁棒状态估计方法,以进一步提高配电网状态估计的精度,综合提升大电网运行的安全稳定性。
1 基于加权最小绝对值的鲁棒状态估计方法
1.1 加权最小绝对值估计
电力系统状态估计的量测方程为:
式中:z为m(m>0)维量测向量;h(x)为非线性函数向量;x为n维状态向量;ε为量测误差向量。
传统WLS状态估计无抗差能力,本文应用目前广泛使用的WLAV抗差估计器,其数学模型为:
式中:w为量测量z的m维权重向量。
添加松弛变量l和u,消除目标函数中的绝对值量,WLAV抗差估计模型为[6]:
构造式(3)的拉格朗日函数:
式中:η、α、β为拉格朗日乘子。
当L最小时,对式(4)的KKT条件泰勒展开,获得修正方程为:
式中:Lx=?坠L/?坠x,其他依次类推;μ为任一正数;A、B、L、U分别为以α、β、l、u为对角元素的对角阵。
将式(11)代入式(5)和式(8)降维后得到修正方程的矩阵形式为:
迭代求解式(11)和式(12)直至满足收敛条件,即可获得状态量的WLAV估计结果。
1.2 噪声参数设置
1.2.1 高斯噪声
本文所采取的高斯噪声模型为:
式中:μ为随机量l的平均值;σ为l的标准差。
本文针对功率噪声的标准差设为0.01,电压幅值的噪声标准差设为0.001。
1.2.2 非高斯噪声
由于噪声的随机性较强,在本文非高斯噪声条件的测试环境下,设置了-10δ~10δ倍的随机误差数据用于模拟不良数据,进一步测试本文方法的鲁棒性,其中δ为标准差。
2 WLAV状态估计流程
在配电网标准算例潮流计算的基础上,本文通过对功率及电压数据添加噪声来模拟实际量测数据,具体鲁棒状态估计过程如下:
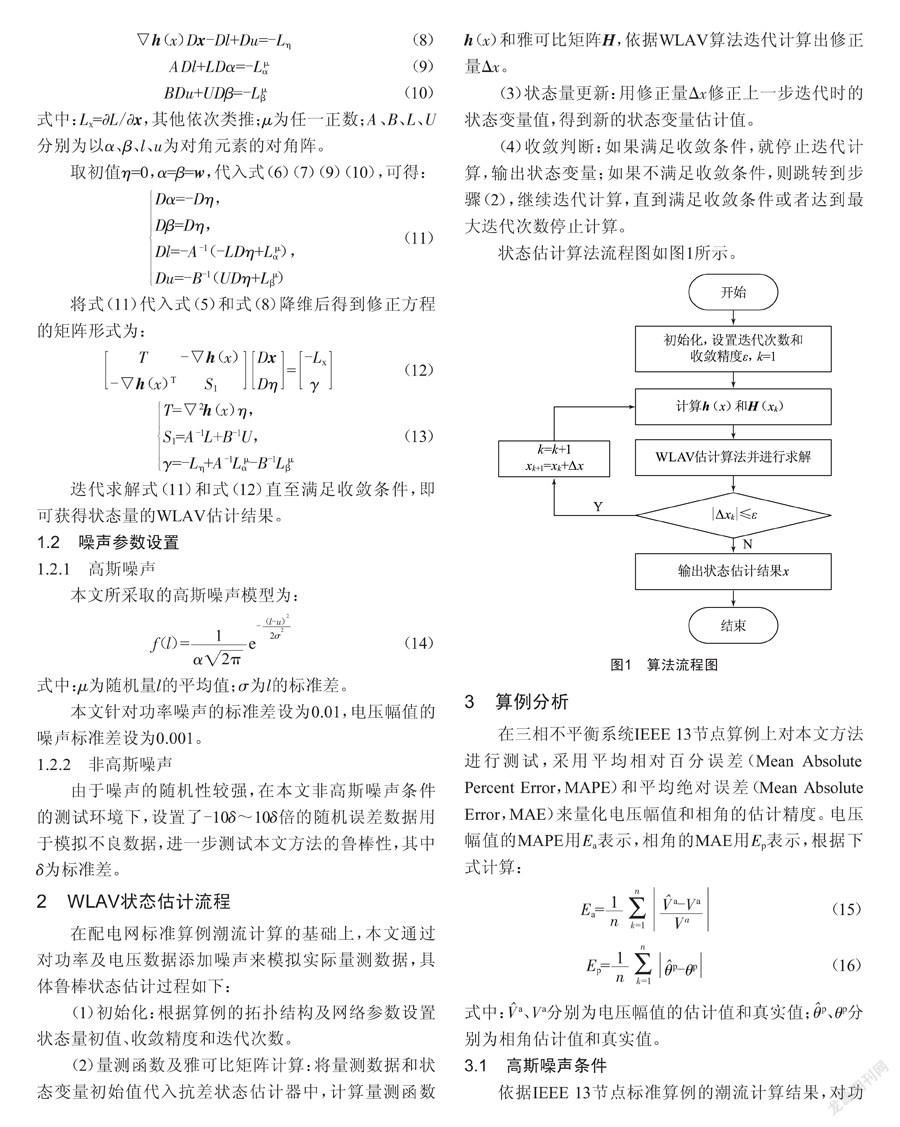
(1)初始化:根据算例的拓扑结构及网络参数设置状态量初值、收敛精度和迭代次数。
(2)量测函数及雅可比矩阵计算:将量测数据和状态变量初始值代入抗差状态估计器中,计算量测函数h(x)和雅可比矩阵H,依据WLAV算法迭代计算出修正量Δx。
(3)状态量更新:用修正量Δx修正上一步迭代时的状态变量值,得到新的状态变量估计值。
(4)收敛判断:如果满足收敛条件,就停止迭代计算,输出状态变量;如果不满足收敛条件,则跳转到步骤(2),继续迭代计算,直到满足收敛条件或者达到最大迭代次数停止计算。
状态估计算法流程图如图1所示。
3 算例分析
在三相不平衡系统IEEE 13节点算例上对本文方法进行测试,采用平均相对百分误差(Mean Absolute Percent Error,MAPE)和平均绝对误差(Mean Absolute Error,MAE)来量化电压幅值和相角的估计精度。电压幅值的MAPE用Ea表示,相角的MAE用Ep表示,根据下式计算:
3.1 高斯噪声条件
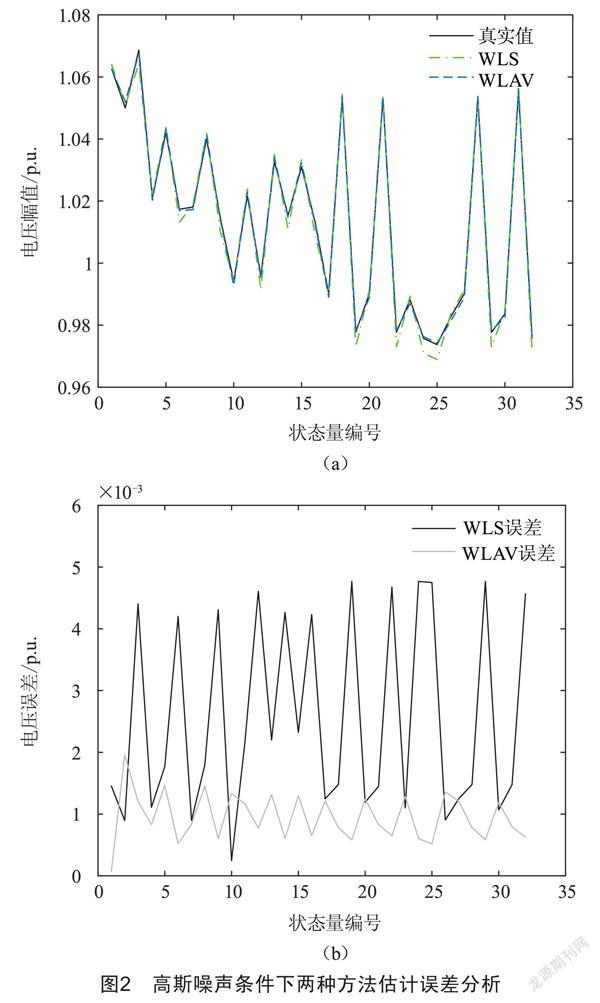
依据IEEE 13节点标准算例的潮流计算结果,对功率量测随机添加均值为0、标准差为0.01的高斯噪声,对电压量测随机添加均值为0、标准差为0.001的高斯噪声。将本文方法与传统最小二乘法进行对比,结果如图2所示。
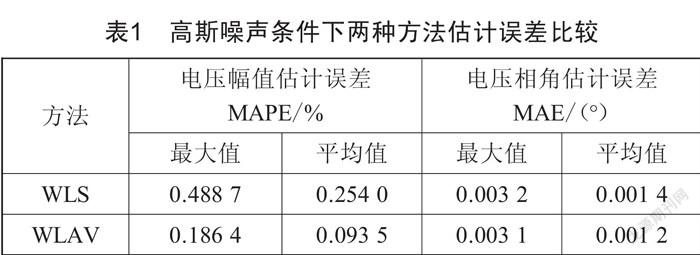
如表1所示,由于传统WLS状态估计无抗差能力,所以在添加随机噪声的情况下,WLAV算法显然具备更高的估计精度。量测系统采集的实时数据要经过多个环节才能传递到主站系统,所以在数据传输的过程中存在的干扰因素非常多,往往需要采用抗差性更强的估计算法来提高计算结果的可信度,从而提高电网调度的准确性。
3.2 非高斯噪声条件
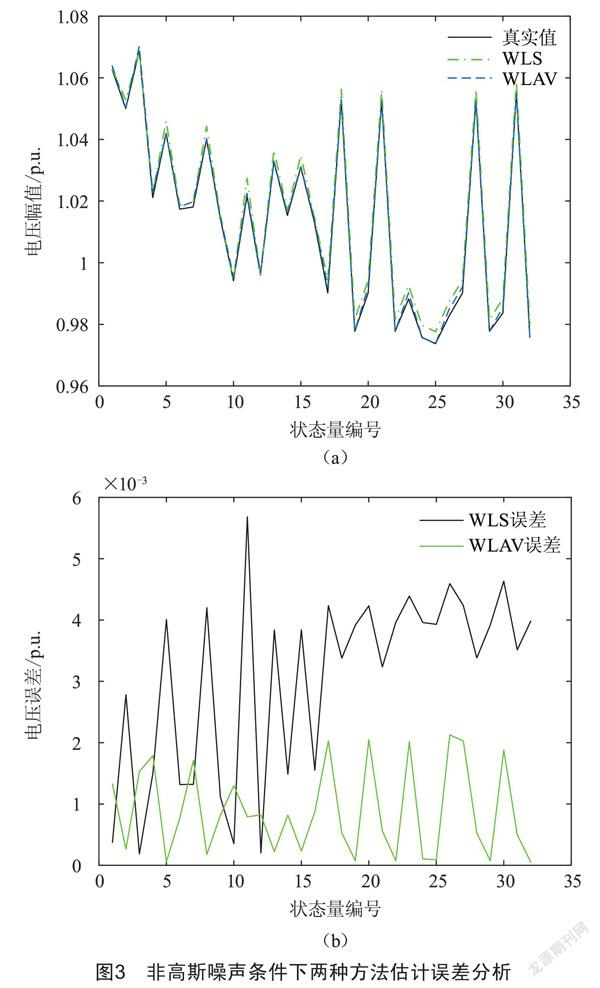
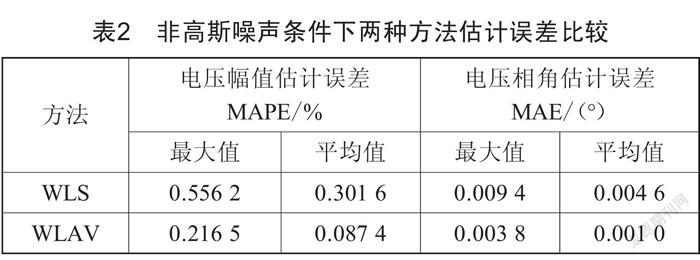
在10%的量测处随机添加-10δ~10δ误差,分析非高斯噪声条件下的估计结果,如图3所示。
如表2所示,传统WLS状态估计在存在较大坏数据时,其估计精度受影响较为严重,在实际配电网的运行过程中,量测系统中可能存在误差较大的不良数据,这些不良数据并不服从高斯分布。在不能将这些不良数据剔除的情况下,WLAV状态估计可以提高估计精度。
4 结语
随着配电网规模的不断发展,调度系统对状态估计的要求也越来越高。实时采集的量测数据往往受到多方面因素的影响,从而影响最终估计的精度,本文测试了多种噪声情况下基于加权最小绝对值的鲁棒状态估计方法,测试结果表明,其相比于传统最小二乘法精度更高,抵御粗差的能力更强。随着大电网的不断发展,不良数据的检测与辨识愈发重要,鲁棒状态估计将在多种场景下具有更加广阔的应用前景,从而为调度系统提供更加准确实时的全网运行状态信息。
[参考文献]
[1] 徐艳春,刘晓明,李振华,等.PMU准实时数据对主动配电网抗差估计的影响[J].电力自动化设备,2020,40(10):15-22.
[2] 郑文迪,聂建雄,邵振国,等.智能配电网状态估计研究现状和展望[J].电力系统及其自动化学报,2021,33(4):8-16.
[3] 颜全椿,卫志农,孙国强,等.基于多预测校正内点法的WLAV抗差状态估计[J].电网技术,2013,37(8):2194-2200.
[4] 鄭顺林,刘进,陈艳波,等.基于加权最小绝对值的电-气综合能源系统双线性抗差状态估计[J].电网技术,2019,43(10):3733-3744.
[5] 李扬,李京,陈亮,等.复杂噪声条件下基于抗差容积卡尔曼滤波的发电机动态状态估计[J].电工技术学报,2019,34(17):3651-3660.
[6] 厉超,卫志农,倪明,等.基于变量代换内点法的加权最小绝对值抗差状态估计[J].电力系统自动化,2015,39(6):48-52.
收稿日期:2022-03-07
作者简介:施雅媛(1988—),女,江苏无锡人,工程师,研究方向:电气工程及其自动化。
