改进系统布置设计法在车间布局设计中的应用
2022-06-14张广泰郭俏君张梅张梦王健
张广泰, 郭俏君, 张梅, 张梦, 王健
(新疆大学建筑工程学院, 乌鲁木齐 830047)
现代化国家中制造业创造了大部分的财政收入,制造车间中零件的搬运可产生大量制造成本,良好的布局设计能减少成本与运营费用,有助于提高制造车间的整体效率。系统布置设计(systematic layout planning, SLP)作为目前应用最广泛的车间布局方法,其综合考量车间设施之间的物流与非物流关系,对物流设施进行合理规划,有效地缩短了生产周期[1]。相关应用研究包括,Shubham等[2]用SLP方法对某车辆制造、维修厂区的布局进行优化,达到减少运输距离和降低搬运成本的目标;Pedro等[3]用SLP方法,对智利圣地亚哥大学的实验场所进行了布局;周佳庆等[4]用SLP方法确定了狭小地铁施工场地的布局方案,为繁华城区地铁施工提供帮助;吕超等[5]结合仿真技术,以SLP方法对混流装配系统布局结构进行了优化。但使用SLP方法过程中,改进布局时需通过反复手工调整,在面对较多的划分区域时将耗用较长时间。为了适应更多的应用场景、满足更高效的布置需求,SLP方法也被不断调整与改进。Phuoc等[6]结合SLP和数学建模的方法,在建筑信息平台对多目标动态临时施工现场平面进行布置;张永强等[7]结合SLP方法和搬运系统分析法,设计了高效的林产品仓储布局方案;张宏斌等[8]对作业单元较多的场景提出自动化排布算法,增强SLP方法的有效性。在研究中学者发现SLP方法主观性较强,往往需要手工调整导致工作量较大,而遗传算法(genetic algorithm, GA)具有全局寻优能力较强、可并行计算、不依赖于梯度信息等特征,故结合GA对其进行优化,为SLP法赋予高效性与合理性,弥补其主观性强、结果不稳定等缺点[9]。Su等[10]通过GA改进SLP方法,对客船船舱进行了优化布局;韩昉等[11]研究得出SLP法与GA结合运用比仅用SLP法的原方案更优;贾佳等[12]以工人劳动强度作为SLP初始布局的重要参考,初步优化SLP法后再将GA与SLP方法结合进行车间布局优化设计。杨涛[13]运用SLP法得到初始布局后,以运输成本与非物流关系为目标函数,运用GA求解,得到优化后的设施布局方案;汪一筇等[14]以总物料搬运成本为目标函数,运用SLP法结合GA求解车间设备布局。
随着研究的深入,发现GA自身存在诸多弊端,如解的易早熟收敛慢、局部搜索能力差与易陷入局部最优等问题[15],仅将GA与SLP法结合应用到车间布局中还存在一定的限制因素,针对该问题,现采用熵权-逼近理想解排序法(entropy weight-technique for order preference by similarity to an ideal solution,ET)组合优化模型对GA中选择算子的计算方式进行改进,此外,在车间布局规划中目标函数大都考虑物流成本为单一约束条件,而在实际的应用中,车间布局需综合考虑物流运输成本、非物流密切程度以及物料搬运时间等因素。因此,将上述三种因素综合考虑提出了多目标规划数学模型,并采用ET-GA算法进行求解,有助于改善GA 的“早熟”问题和SLP的缺陷,最后借助案例说明改方法的有效性。
1 车间布局设计模型
1.1 模型假设
进行车间布局设计时,由于各作业单位形状及面积均不同,考虑布局设计以及软件模拟,在建模时提出以下合理假设:①假设该光伏组件厂各作业单位均在该车间空间范围内,且各作业单位的形状均是矩形,各作业单位的面积均已知;②各作业单位之间的相互距离除了考虑实际情况之外均采用曼哈顿距离。
基于此,车间布局问题作为场景特殊的布局优化问题,在连续空间中满足一定假设前提和约束条件,其拓扑结构图如图1所示。
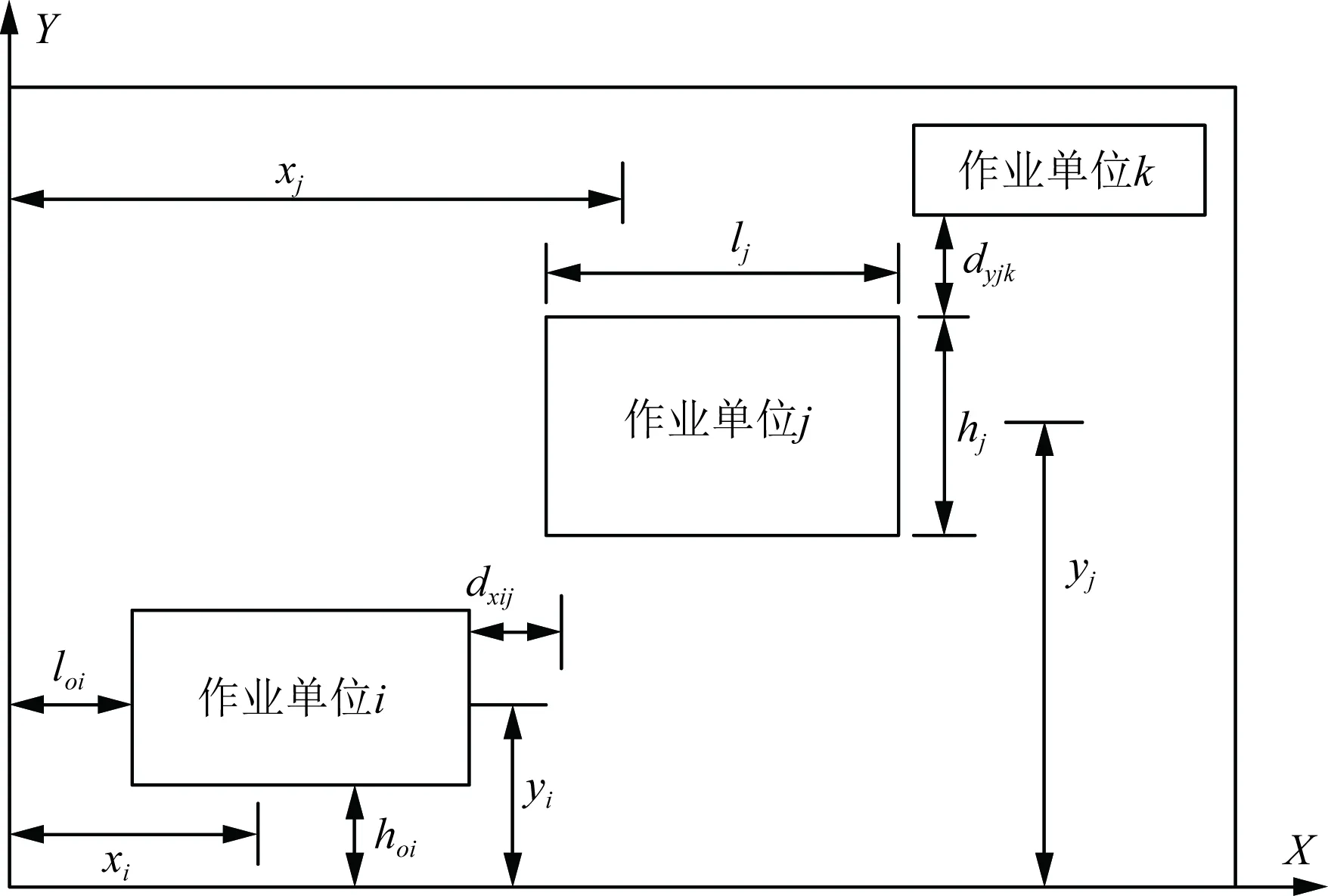
X轴为生产车间的长度方向;Y轴为生产车间的宽度方向;L为生产车间的长度;W为生产车间的宽度;作业单位i,j,k,…,n为车间存在的作业单位;(xi、yi)为作业单位i在X轴、Y轴的中心坐标;lj为作业单位j在X轴方向的长度;hj为作业单位j在Y轴方向的宽度;loi为作业单位Y轴方向上的最小距离;hoi为作业单位X轴方向上的最小距离;dxij为作业单位i与作业单位j在X轴方向上的距离;dyjk为作业单位j与作业单位k在Y轴方向上的距离图1 车间和作业单位的拓扑结构图Fig.1 Topological structure diagram of workshop and operation unit
1.2 目标函数
综合考虑车间实际情况,布局设计目标为使得各作业单位之间物流运输成本(F1)最低、非物流密切程度(F2)最大与物料搬运时间(F3)最小,公式为

(1)
式(1)中:N为作业单位总数;cij为作业单位i到j的搬运成本;qij为作业单位i到j的平均物流量;dij为作业单位i到j的距离,满足dij=|xj-xi|+|yj-yi|;vij为作业单位i至作业单位j的搬运速度;bij为作业单位i与j之间的接近程度;Tij为作业单位i与j之间的非物流关系值,其数值来源于各作业单位密切程度等级量化结果,量化规则见表1。

表1 作业单位相互关系密切程度等级量化表Table 1 The level of closeness of interrelationship between operating units
bij表示作业单位i与j之间的接近程度,即关联因子或关联度,其值由dij实际大小界定获得,bij值的界定方法见表2。
为了简化计算,将式(1)转化为一个单目标函数,引入归一化因子μ1、μ2和μ3统一搬运成本、非物流密切程度和搬运时间的不同量纲;引入权值ω1、ω2和ω3调整F1、F2和F3目标函数的比重,ω1、ω2和ω3的值由专家根据生产车间实际情况打分确定,且ω1+ω2+ω3=1。由此简化得到的单目标函数为
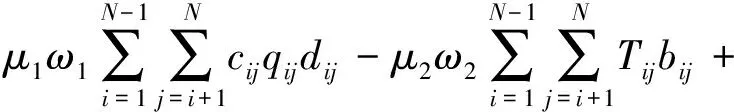
(2)
式(2)中:归一化因子

表2 关联因子的界定Table 2 Definition of correlation factors
1.3 约束条件
根据实际情况,模型的车间设施将多行分布,设计决策变量Zik(i=1,2,…,n;k=1,2,…,m,m为设施排布的总行数),Zik计算方式为

(3)
由于布局过程中同一行、列所布置设施的长度之和、宽度之和不能超过该车间的总长度、总宽度,设施离车间四周还需要保持一定安全距离。故设施定位需满足式(4)和式(5),即

(4)
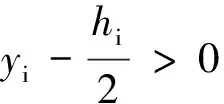
(5)
为保证生产车间各作业单位能进行正常的生产运作,所有的车间设施均不能重叠,且需保持一定的距离d(如图1中dxij和dyjk)。故水平方向上需满足式(6)、垂直方向上需满足式(7),即

(6)
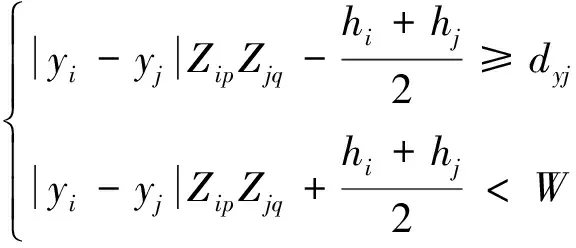
(7)
式中:si为在X轴方向上的长度;sj为在Y轴方向上的长度。
2 改进SLP法
2.1 ET模型
熵权-TOPSIS模型实现了熵权系数评价与TOPSIS决策的集成,原理为先用熵权法求出评估对象各评价指标的权重,再用TOPSIS法计算各评价指标与正、负理想解的相对距离,最终排序方式依据相对距离大小。近年来,ET模型在布局设计中存在相应的应用,徐银凤[16]以长江经济带交通接驳系统为研究对象,用ET模型对37个城市高铁枢纽进行了接驳绩效评价;罗静[17]通过ET模型分析了沥青再生工厂不同布局方式对环保水平的影响。
步骤1收集评估对象相关评价指标的原始资料,则评价体系的原始特征值矩阵形式为

(8)
式(8)中:n为评估对象的个数;m为评价指标的个数;xij为第j个评估方案在第i个评价指标上的评分。
步骤2为了消除量纲,标准化处理特征值矩阵,得到标准化矩阵(yij)m×n形式为

(9)
步骤3由式(10)计算各评价指标的熵值Hi,公式为
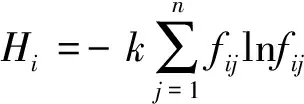
(10)
步骤4由式(11)计算评价指标的熵权。

(11)
步骤5采用欧氏距离公式[式(12)]计算评估目标到正、负理想解的距离
和
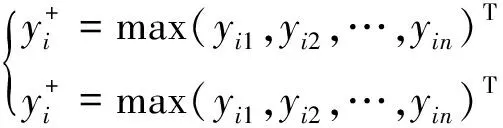
(12)
步骤6由式(13)计算评估对象的优属度uj,进行综合排序,uj越大,排序越高。
(13)
2.2 GA算法
遗传算法(GA)通过模拟生物遗传机理(自然淘汰、交叉、变异等)进行随机搜索与进化,最终寻求近似最优解[18]。较强的全局寻优能力与通用性使得GA逐渐成为处理车间布局问题的重要方法。GA流程图如图2所示,首先通过染色体编码如直接编码、二进制编码或参数化编码将解空间的解数据编码为串结构数据即染色体基因,再初始化种群即随机生成n个可行解,对种群中个体适应度进行评估,若适应度满足终止条件,则解码并作为近似最优解输出,若适应度不满足,用GA规则进行选择、交叉、变异操作产生子代解,直到适应度满足为止。
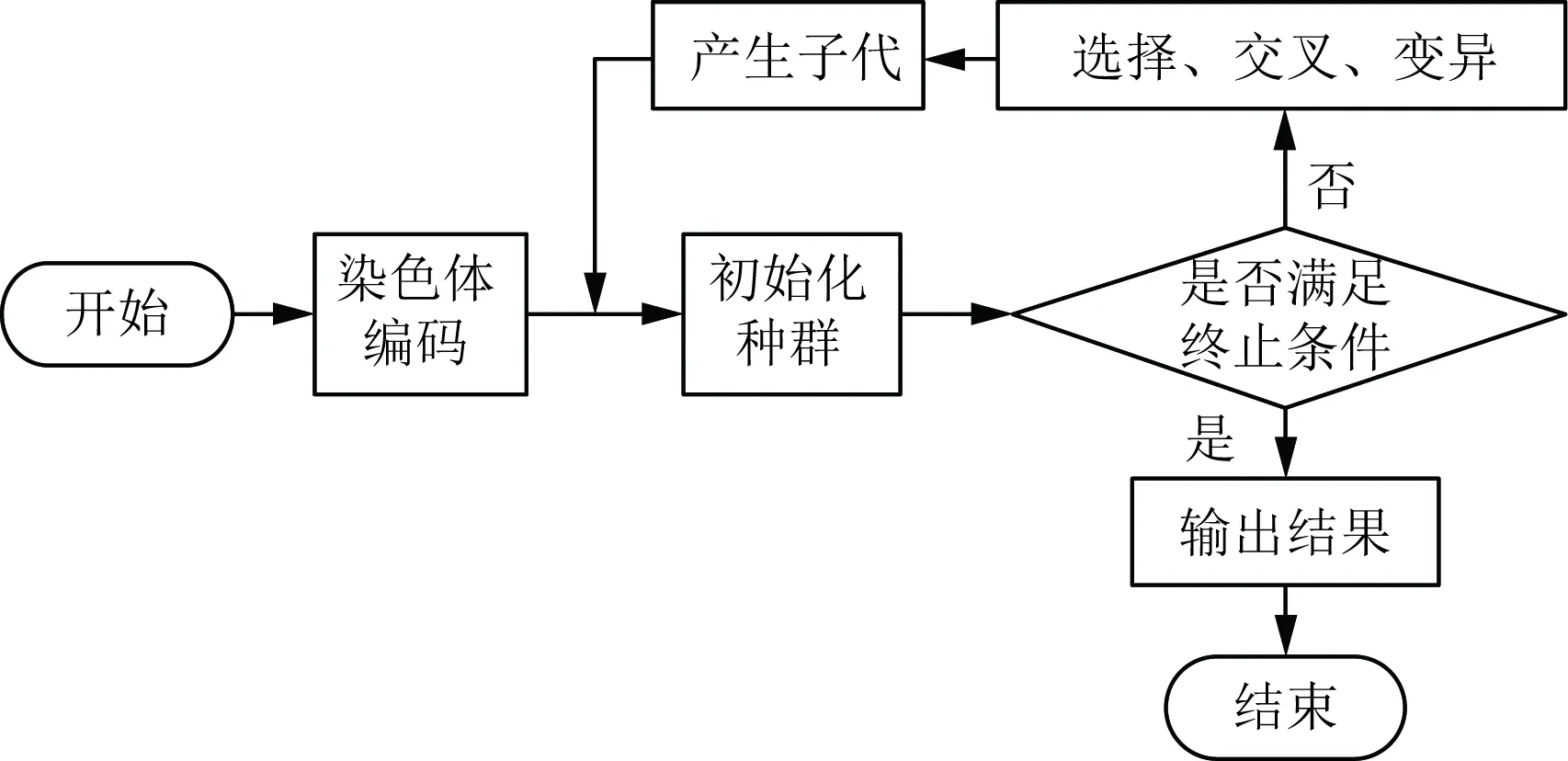
图2 GA流程图Fig.2 Flow chart of genetic algorithm
2.3 ET-GA算法
GA具有较好的全局搜索能力,但易早熟、局部搜索能力不足,在优化较为复杂的问题时容易陷入局部最优,反映到实际问题中则为收敛慢,易陷入局部最优而导致无法有效寻找到最满意解[19-20],针对GA的不足之处,葛晓梅等[21]引入进化逆转操作提高GA局部寻优能力,更好地解决了车间布局问题;张青雷等[22]提出自适应GA,运用精英保留策略使其免于陷入局部最优,有效降低了车间物流费用和时间。郭岳[23]运用换方变换改变GA的编码规则提高了GA的求解能力;陈思远等[24]运用指针网络改进GA初始种群,结果表明优化后算法收敛率与寻优能力显著提高。现有文献对GA的改进较多集中在初始种群优化、交叉与变异等方面,而对GA选择算子的改进研究则不够充分。在前人研究基础上,通过ET模型对GA算法中选择算子优化,形成ET-GA算法。
GA常用适值比例法确定染色体是否发生变异,该方法也称轮盘赌或蒙特卡罗模型,是根据每个染色体适值比例确定其被选中或生产的概率。染色体对应的选择概率pk和累计概率qk,popSize为种群规模(j=1,2,…,popSize),计算公式为
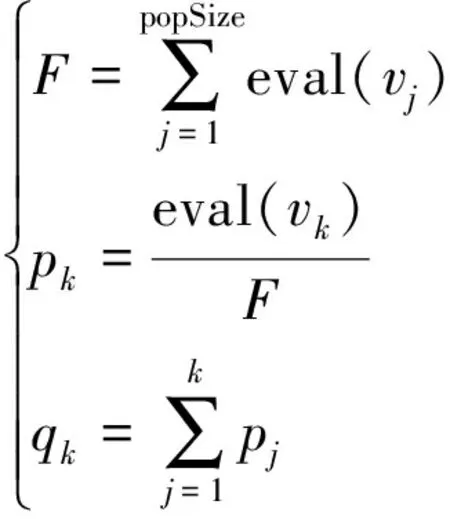
(14)
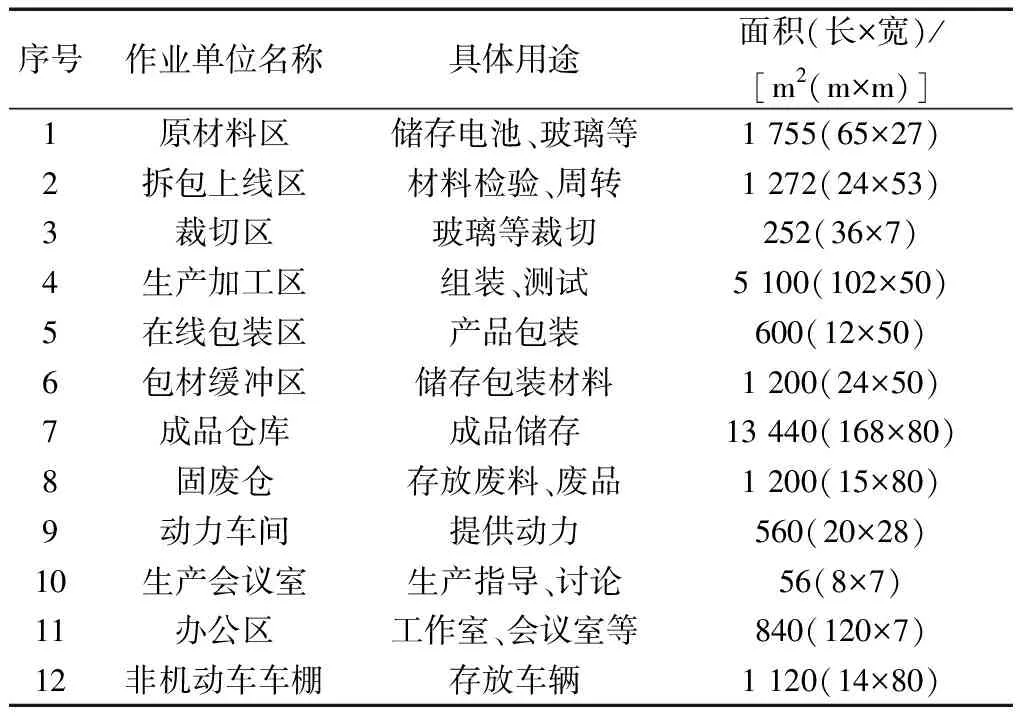
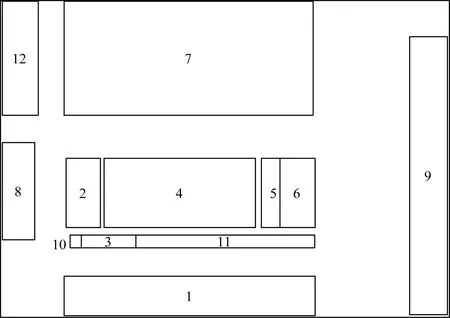
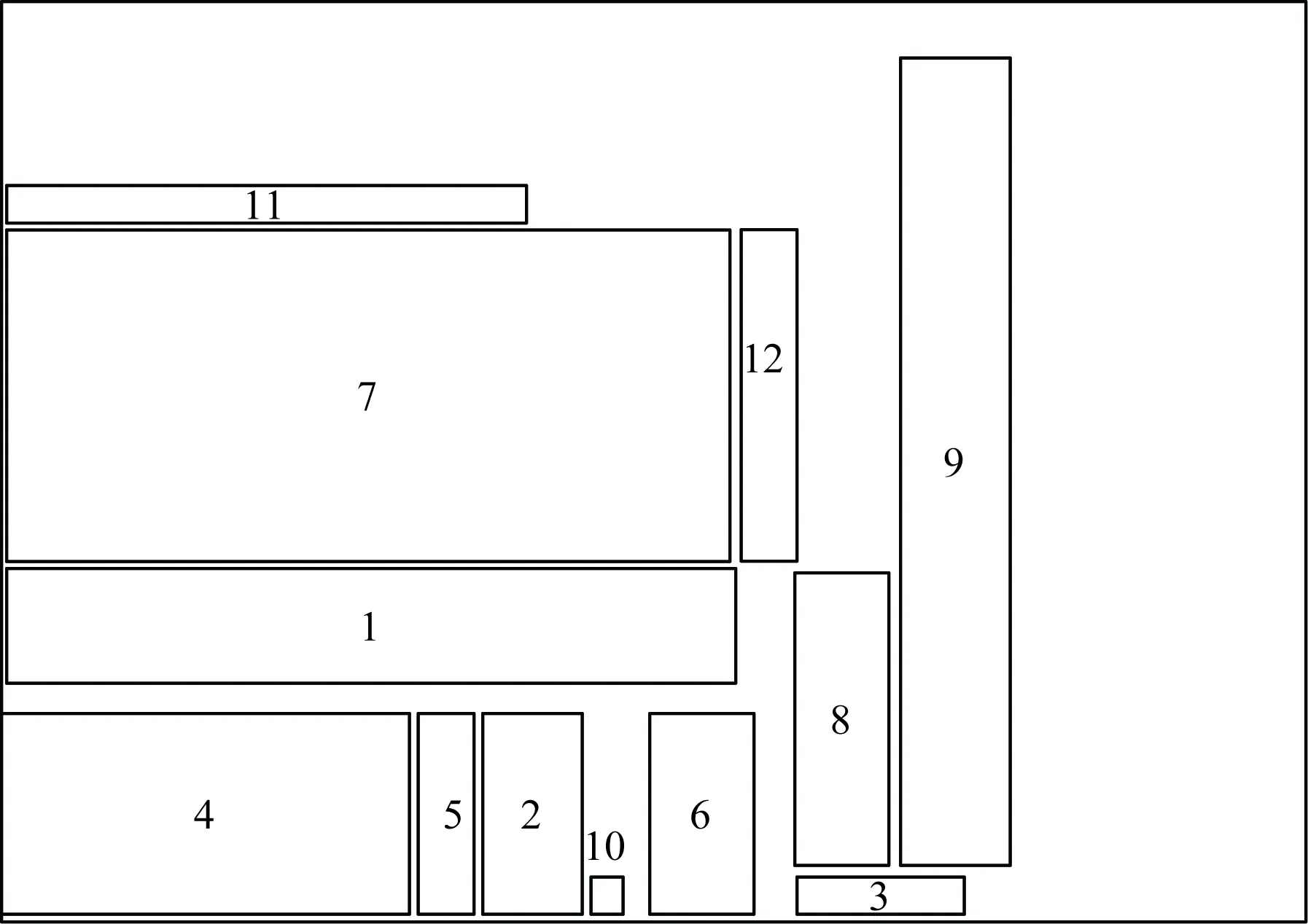
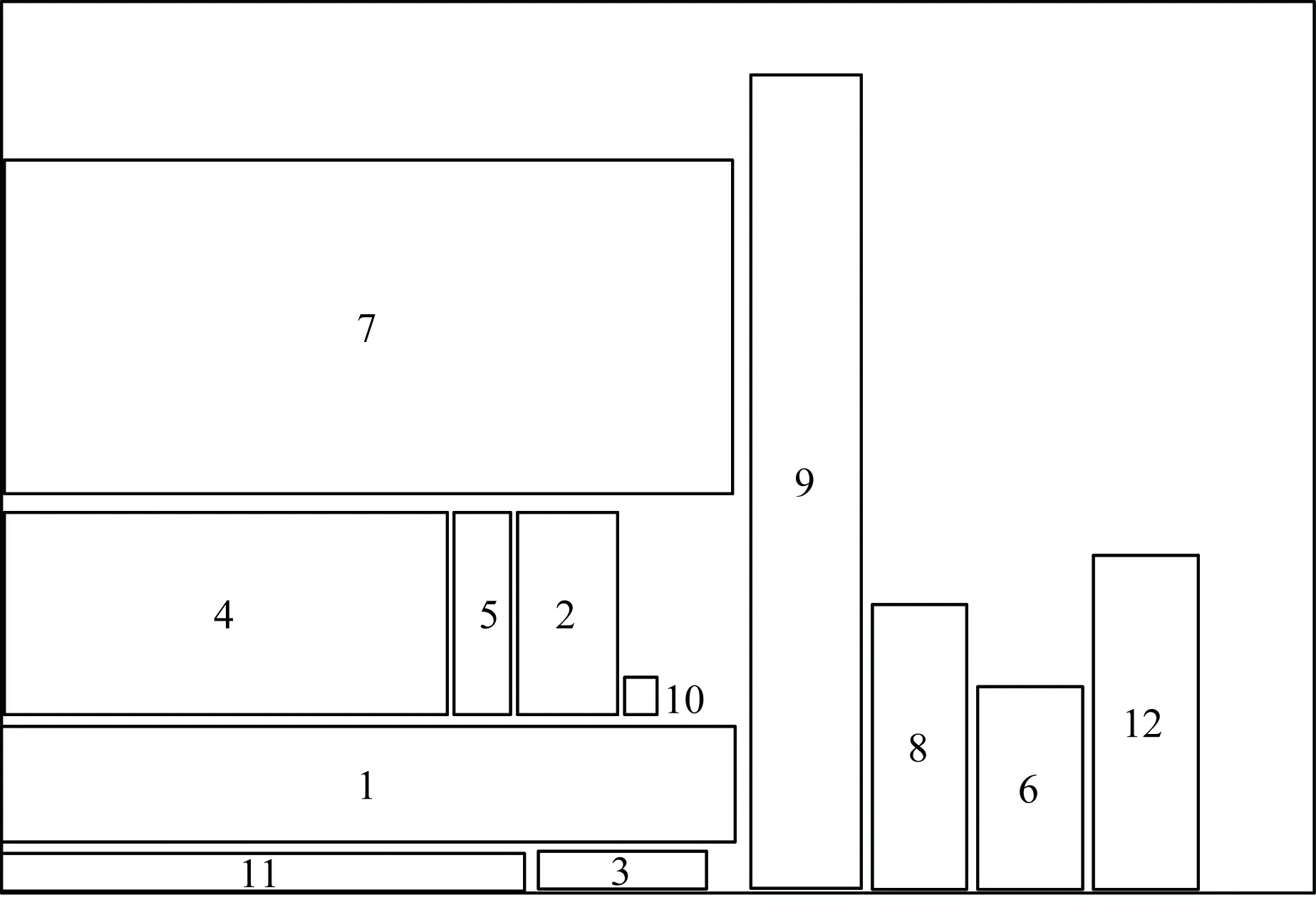
式(14)中:k为染色体的索引号;vk为第k个染色体;eval(vk)为该染色体适应值;F为所有染色体的适应值之和;pk为第k个染色体的选择概率;qk为前k个染色体的累计概率。选择染色体的方式为:在[0,1]内产生一个随机实数rk,当rk﹤q1时,则选择v1作为v′k;当qi-1 GA算法在遗传算子的选择步骤中使用轮盘赌模型存在一定的局限性,特别是在每个个体适应度值相差较小的情况下,其基于概率选择随机性可能将较优的个体在进化中遗弃,种群质量随之降低,这将造成收敛慢与早熟等问题。将ET模型引入GA优化选择算子,有效地将个体适应度进行了区分,最大化地降低了选择算子淘汰染色体时的不确定性,尽可能地保留了适应度较高的个体,使得在种群数量一定的情况下跳出局部最优解进一步提高了算法的收敛效率,具体优化步骤与机理如下。 步骤1对染色体适应值eval(vk)进行式(15)操作得到yk。 (15) 式(15)中:min(eval)为所有染色体中适应度的最小值。 步骤2由式(16)计算每个染色体适应值的熵值Hk。 (16) 步骤3由式(17)计算染色体适应值的熵权wk。 (17) 步骤4由式(18)计算染色体的优属度uk。 (18) 步骤5由式(19)计算染色体累计绩效qk。 (19) 步骤6进行下一代染色体选择。在[0,1]区间内产生一个随机实数rk,当rk﹤q1时,则选择v1作为v′k;当qi-1 采用ET-GA算法对SLP方法进行改进:首先,根据SLP方法确定原始资料的初始条件;其次,建立物料搬运成本、非物流关系与物流搬运时间的多目标优化数学模型;最后,用提出的ET-GA算法进行数学模型求解得到最优布局方案。通过ET-GA算法改进后的SLP方法,不仅具有SLP方法的系统性与逻辑性、GA较好的全局搜索能力,还克服了GA易早熟与收敛慢的弊端。改进SLP方法流程图如图3所示。 SLP法原始资料收集包含的要素含义为:P表示产品、物流与服务;Q表示每种物品的数量;R表示生产工艺路线;S表示辅助服务部门;T表示时间图3 改进SLP方法的车间布局设计流程Fig.3 Workshop layout design process based on improved SLP method 分析对象为一间主要生产太阳能设备的光伏组件厂,作业场地占地面积约为67 500 m2,计算时将其简化为长约300 m、宽约225 m的矩形。根据产品实际生产过程,作业场地内存在12个作业单位,其详细信息如表3所示,初始单位布局如图4所示。 通过对光伏组件厂进行调研及员工访问,结合其生产工艺过程和车间布局现状(图4),发现该厂布局不合理,部分作业单位如原材料与生产加工区之间过远,致使物料搬运需要通过较长的路程,也存在路线往返交叉的现象;办公区与生产区间隔太小,致使产生的噪声、振动等对办公效率有负面影响,且存在一定的安全隐患;生产单位整体布局不够紧密,不利于提高生产效率。 为此,引入改进SLP方法进行车间设施重布局。根据光伏组件厂的实际生产情况,Y轴方向上作业单位的最小距离loi=3 m;X轴方向上作业单位的最小距离hoi=3 m;权重ω1=ω2=ω3=0.4。各作业单位的物流搬运量qij见表4,搬运成本cij为0.007 8元/(托盘·m),搬运速度vij为2.22 m/s。 表3 作业单位信息汇总表Table 3 Job unit information summary table 图4 初始布局图Fig.4 Initial layout diagram 运用ET-GA算法求解目标函数,对车间布局进行优化设计。其参数设置为:种群规模M=100,交叉概率Pc=0.9,变异概率Pm=0.1,迭代次数G=500。最终求解结果得到1~12设施坐标为:(91,75)、(139,29)、(207,11)、(51,25)、(110,25)、(168,24)、(96,128)、(195,47)、(220,103)、(152,2)、(60,162)、(175,128),该车间布局优化方案如图5所示。 根据改进SLP方法的车间布局结果,与初始布局对比后可知,优化的布局更紧凑、生产单位之间距离更小;原材料区处于中心位置,与各生产单位之间的联系将更便捷;固废区、动力车间、非机动车车棚等具有一定噪声或污染的单位被布置在边缘位置,减弱其对整个车间的影响;生产会议室、办公区等也布置在边缘位置,免受生产单位的干扰。综合来看,优化后布局更具科学性、合理性,可进一步激发员工生产效率、保障员工工作环境的健康与安全。 图5 基于ET-GA算法的车间布局优化方案Fig.5 Optimization scheme of workshop layout based on ET-GA algorithm 为了验证ET-GA算法改进SLP方法的有效性,设计只用GA算法优化SLP方法的实验,实验参数同第一次实验,对比两次求解的结果。根据对照实验结果,GA、ET-GA算法目标函数迭代过程如图6所示,GA算法改进SLP方法的车间布局优化方案如图7所示。 图6 两种算法目标函数迭代曲线对比图Fig.6 Comparison of iterative curves of objective function of two algorithms 图7 基于GA算法的车间布局优化方案Fig.7 Optimization of workshop layout based on GA algorithm 表4 作业单位物流/托盘(关系等级)Table 4 Operation unit logistics/pallet (relationship level) 由图6可知,ET-GA算法虽在发现近似最优解的速度方面稍慢于GA,但ET-GA算法拥有更好的近似最优解。这是由于GA局部搜索能力比较差,易出现早熟收敛现象,导致所得到的解可能并非近似最优解。而ET-GA算法优化模型对选择算子进行改进,提高搜索近似最优解的质量、避免早熟现象,在解决车间布局问题中具有良好的效果。对比分析初始布局方案、基于ET-GA算法的SLP方法得到的布局方案、基于GA算法的SLP方法得到的布局方案(图4、图5和图7),从搬运成本、非物流关系和搬运时间3个方面用MATLAB软件进行仿真计算、对比分析,计算结果如表5所示。 表5 方案结果对比分析Table 5 Comparative analysis of the results of schemes 由表5可知,基于ET-GA算法的SLP车间布局方案与原方案、基于GA的SLP布局方案相比,物料搬运成本分别节约了12.50%、5.88%,非物流关系分别提高了3.72%、2.50%,物料搬运时间分别降低了21.02%、14.75%,验证了提出的基于ET-GA的改进SLP方法可以使得车间布局物流搬运成本更低、非物流关系更大及物流搬运时间更小。 采用ET模型对GA中选择算子进行重新计算,形成ET-GA算法改进SLP方法,并通过光伏组件厂实例研究对提出算法的可行性进行验证。验证结果显示ET-GA算法较GA寻优能力更强、近似最优解的质量更好,物料搬运成本、非物流关系、物料搬运时间均得到改善,改进SLP方法得到的布局方案较原布局方案更具科学性、安全性、合理性。本文方法能有效地进行车间布局设计,以提高生产效率、降低生产成本、缩短物料搬运时间,还可为制造企业新建或改扩建生产车间提供布局设计依据。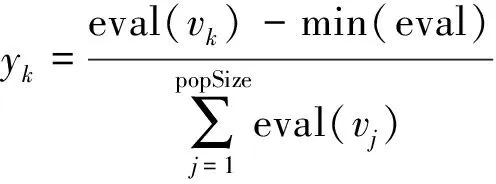
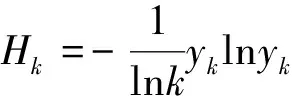

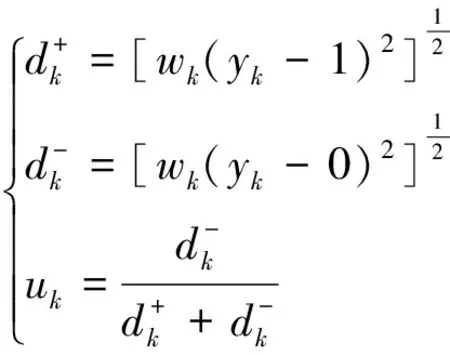
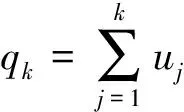

3 案例分析
4 数值分析



5 结论
