基于建筑虚拟储能的分布式能源系统优化调度

叶家盛， 刘青荣*， 阮应君， 钱凡悦， 孟华

(1. 上海电力大学能源与机械工程学院， 上海 200090； 2. 同济大学机械与能源工程学院， 上海 200092)

在环境污染和能源危机的不断加剧情况下，能源结构亟待调整，分布式能源系统具有经济、环境友好、可持续等优点得到国内外普遍关注[1-3]。随着可再生能源技术和分布式能源的推广应用，微电网研究得到快速发展，文献[4]针对可再生能源和负载功率不确定性问题，考虑了多间隔-不确定性约束并对微电网进行了鲁棒调度分析。另外，建筑墙体的隔热作用和空气的蓄热属性使建筑体本身具有较好的热惰性，当电气设备的特征量改变时，室内温度变化存在一定滞后现象[5]。在用户可接受温度范围内调整温度变化曲线可提高冷(热)负荷的灵活性，对优化系统运行成本具有重大意义。针对此类问题，文献[6-7]对空调负荷虚拟储能进行了建模研究，结果表明了虚拟储能策略的优越性和有效性。文献[8]将虚拟储能融合到热电联供综合能源系统中，提出了一种联络线功率波动平抑策略，并通过案例研究表明了该策略的有效性。文献[9]同时建立了电动汽车和建筑虚拟储能模型，并引入区域综合能源系统的优化调度中，建立了以系统日运行费用最小为目标的经济优化调度模型。文献[10]分析了虚拟储能参与电制冷系统和冷热电三联供系统(combined cooling heating and power，CCHP)的优化调度情况。文献[11]考虑了4种不同建筑的混合能源微网，同时基于建筑虚拟储能做了动态经济优化调度和对比分析。

总之，结合虚拟储能的相关研究已经取得一定的成果，在前人的研究基础上，现进一步展开研究，根据热平衡方程建立虚拟储能模型，描述虚拟储能参与系统优化调度的过程。优化调度过程的目标函数兼顾环境成本和综合运行成本，建立以经济性为准则的多目标优化调度模型。通过和不引入虚拟储能的调度情况对比，详细分析虚拟储能对调度结果产生的影响。

1 分布式能源系统数学模型

考虑典型的分布式能源系统，主要包括蓄电池、吸收式制冷机、微型燃气轮机和风机等能量存储和转换设备，其结构示意图如图1所示。

(1)微型燃气轮机模型。

PMT=PfuelηMT

(1)

式(1)中：PMT、Pfuel分别为燃气轮机输出电功率和消耗天然气功率，kW；ηMT为燃气轮机发电效率。

(2)吸收式制冷机模型。

QAR=ηHEλMTPMTCOPAR

(2)

式(2)中：QAR为吸收式制冷机输出功率，kW；ηHE为换热装置效率；λMT为燃气轮机热电比；COPAR为吸收式制冷剂制冷系数。

(3)蓄电池模型。

引入电池荷电状态(state of charge,SOC)，得到模型[12]为

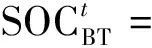
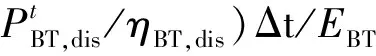
(3)

式(3)中：σBT为电池自放电系数；ηBT,ch、ηBT,dis分别为电池充放电效率；PBT,ch、PBT,dis分别为电池充放电功率；EBT为电池额定容量，kW·h；t为时间。该模型中电池容量为40 kW·h,电池自放电系数取值0.01，充放电效率都取0.95，充电功率和放电功率下限取0 kW，上限取值30 kW。

图1 典型分布式能源系统Fig.1 Typical distributed energy system

(4)建筑虚拟储能模型。

基本描述方程为

ΔQ=CρV(dTin/dt)

(4)

式(4)中：C为空气比热容，J/(kg·℃)；ρ为空气密度，kg/m3；V为建筑体积容量，m3；Tin为室内温度，℃。

考虑影响室内热量的因素主要包括室内外温差造成的温度耗散、室内热源变化、太阳辐射和制冷设备输出功率。将式(4)展开得

(5)

式(5)中:Kwall、Kwin分别为墙、窗传热系数,W/(m2·K)；Swall、Swin分别为墙、窗面积,m2；Tout为室外温度，℃；G为窗外表面的光照强度，kW/m2；Sc为遮阳系数，取值0.3[13]；Qin为室内热源发热功率,kW。

为较好描述虚拟储能，引入虚拟储能充放功率和虚拟荷电状态(state of virtual charge，SOVC)，定义室内温度在最低可接受温度时的虚拟荷电状态为1，在最高可接受温度时为0，虚拟储能模型主要参数如下。

(6)

式(6)中：P为充放功率，kW；E、EB分别为虚拟储能某时刻的容量和额定容量，kW·h；Tin,max、Tin,min分别为室内可接受最大、最小温度，℃；空气比热容取值1 000 J/(kg·℃),空气密度取值1.2 kg/m3。

2 系统优化调度模型

2.1 目标函数

目标函数以日综合成本最低为目标，日综合成本由环境成本和综合运行成本(燃气费用、购售电费用和设备维护费用)构成，目标函数的具体表达式为

F=Ffuel+Fpu+Fom+Fen

(7)

(1)燃气费用。

Ffuel=CfuelPfuel

(8)

式(8)中：Cfuel为天然气价格，元/(kW·h)；取值0.16元/(kW·h)[10]，Pfuel由式(1)确定。

(2)电网交互费用。

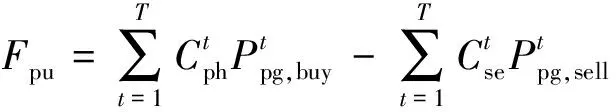
(9)

式(9)中：Cph、Cse为购电、售电价格，元；Ppg,sell、Ppg,buy为售电、购电功率，kW。

(3)设备维护费用。

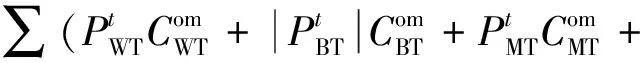
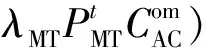
(10)

(4)来源于电网和燃气轮机的环境费用。

Fen=W1C1+W2C2

(11)

式(11)中:W1、W2为电网和微燃机的总购(发)电量，kW·h；C1、C2为电网和微燃机每度电带来的污染气体的总处理费用，元/(kW·h)。

2.2 约束条件

(1)电力平衡约束。

Pex,t+PWT,t+PMT,t+PBT,t=Pel,t

(12)

式(12)中：Pel,t为建筑t时刻电负荷需求,kW；Pex,t为t时刻与电网交互电负荷,kW。

(2)冷负荷平衡约束。

QAR,t=QC,t

(13)

式(13)中：QC,t为建筑t时刻冷负荷，kW。

(3)微型燃气轮机出力约束。

(14)

(4)蓄电池约束。

(15)

(5)建筑热平衡约束。

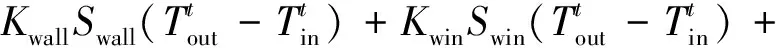
(16)

(6)室内温度约束。

Tin,min≤Tin≤Tin,max

(17)

3 算例

3.1 算例介绍

考虑中国北方寒冷地区办公建筑，以夏季制冷场景为例，引入两种调度模式，模式1考虑建筑虚拟储能，模式2则不考虑建筑虚拟储能。当不考虑虚拟储能时，室内温度在工作阶段(8:00—19:45)为24 ℃并保存不变，当考虑虚拟储能时，室内温度可以在(24±2) ℃范围内波动。该建筑长40 m,宽20 m,每层高3 m，共10层。建筑相关信息如表1所示，其他相关数据信息如图2、图3所示，其中光照强度反映窗户外表面光照情况。燃气轮机容量为100 kW，风电数据参考宁夏某地区2017年夏季风电场数据并结合该建筑规模按比例缩小，工作阶段前一刻室外温度为26.77 ℃。

优化调度过程采用的分时电价[14]如表2所示。基于MATLAB平台构建系统模型，基于Excel制图软件对结果进行图像的绘制，模型的求解主要参考文献[15]所提的帕累托档案多目标粒子群算法。算法的种群大小设置为50，迭代次数为800次，学习因子c1=c2=1.15,初始惯性权重取值0.229 8。在优化调度过程，系统采用以热定电的运行模式并且优先安排风电来满足建筑的电力负荷。

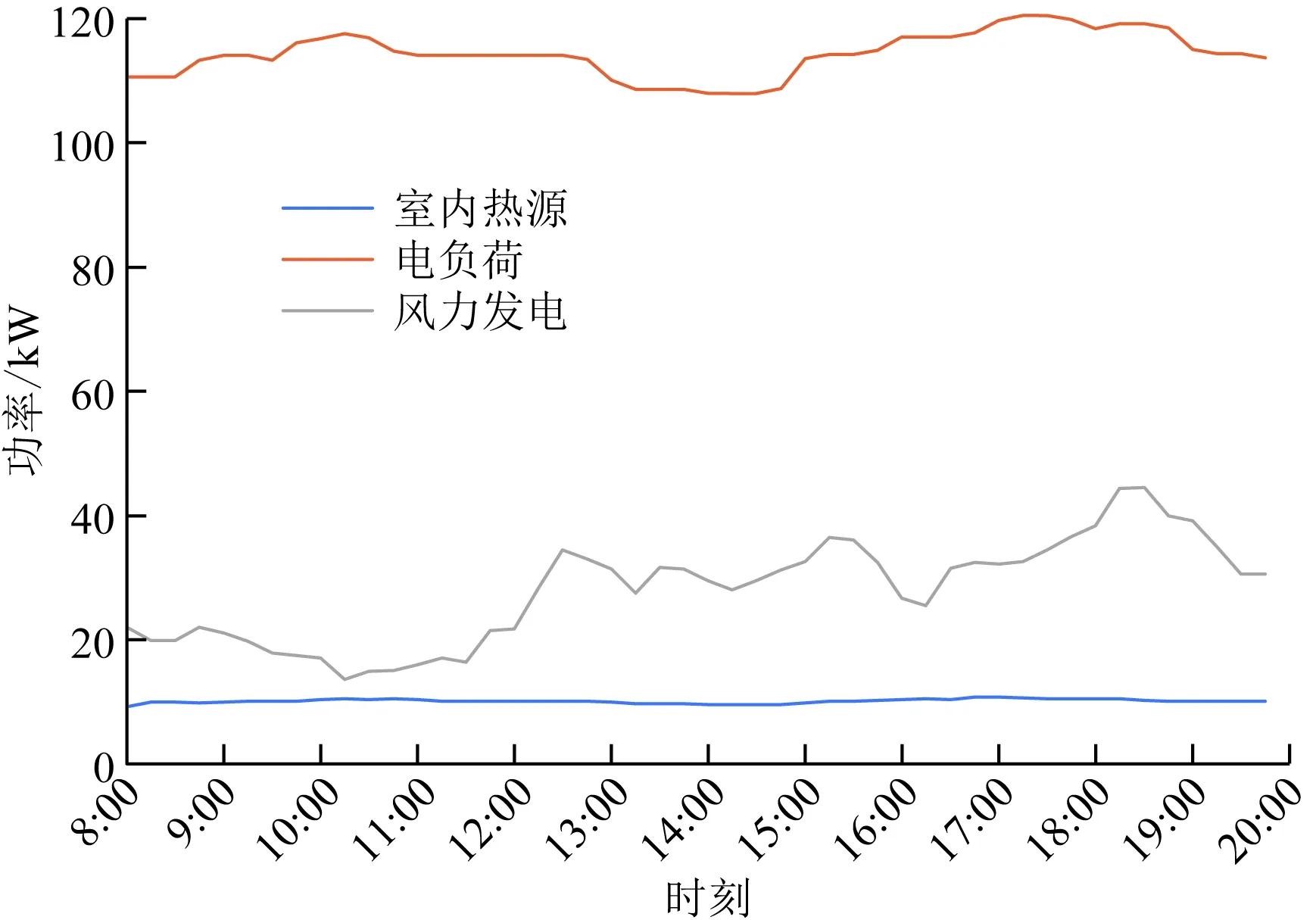
图2 电力负荷、风力发电及室内热源Fig.2 Electric load, wind power generation and indoor heat source

图3 室外温度与光照强度Fig.3 Outdoor temperature and light intensity

表1 建筑参数信息Table 1 Building parameter

表2 分时电价Table 2 Time-of-use electricity price

模型在调度过程考虑的污染物及排放系数主要参考文献[16]，包括二氧化碳[电网的排放系数取值0.889 kg/(kW·h)，燃气轮机取值0.202 kg/(kW·h)]、二氧化硫[电网的排放系数取值为0.001 2 kg/(kW·h)，燃气轮机取值为0]、氮氧化物[电网的排放系数取值为0.001 1 kg/(kW·h)，燃气轮机取值为0]，它们的处理费用分别取值为0.210、14.842、62.964 元/kg。总体表现为电网的环境处理费用C1为0.273 元/(kW·h)，燃气轮机的环境处理费用C2为0.043 元/(kW·h)，其他主要参数的取值如表3所示。

表3 主要参数信息表Table 3 Main parameter information table

3.2 结果及分析

优化调度过程的时间间隔为15 min，图4是两种调度情况下算法求解结果的最优前沿。最优前沿给出了算法搜寻的所有最优解(多目标优化一般不存在唯一最优解，最优解表示的是算法可接受的解)，两种调度结果输出的是前沿中总成本(综合运行成本与环境成本之和)最小的解。

由帕累托前沿可知，单一追求运行费用最小会带来环境成本的增大，所以实际过程考虑环境因素更有实际意义，同时多目标优化过程提供了决策者许多不同的解，决策者可以根据当地环境政策选择最合理的调度方案。

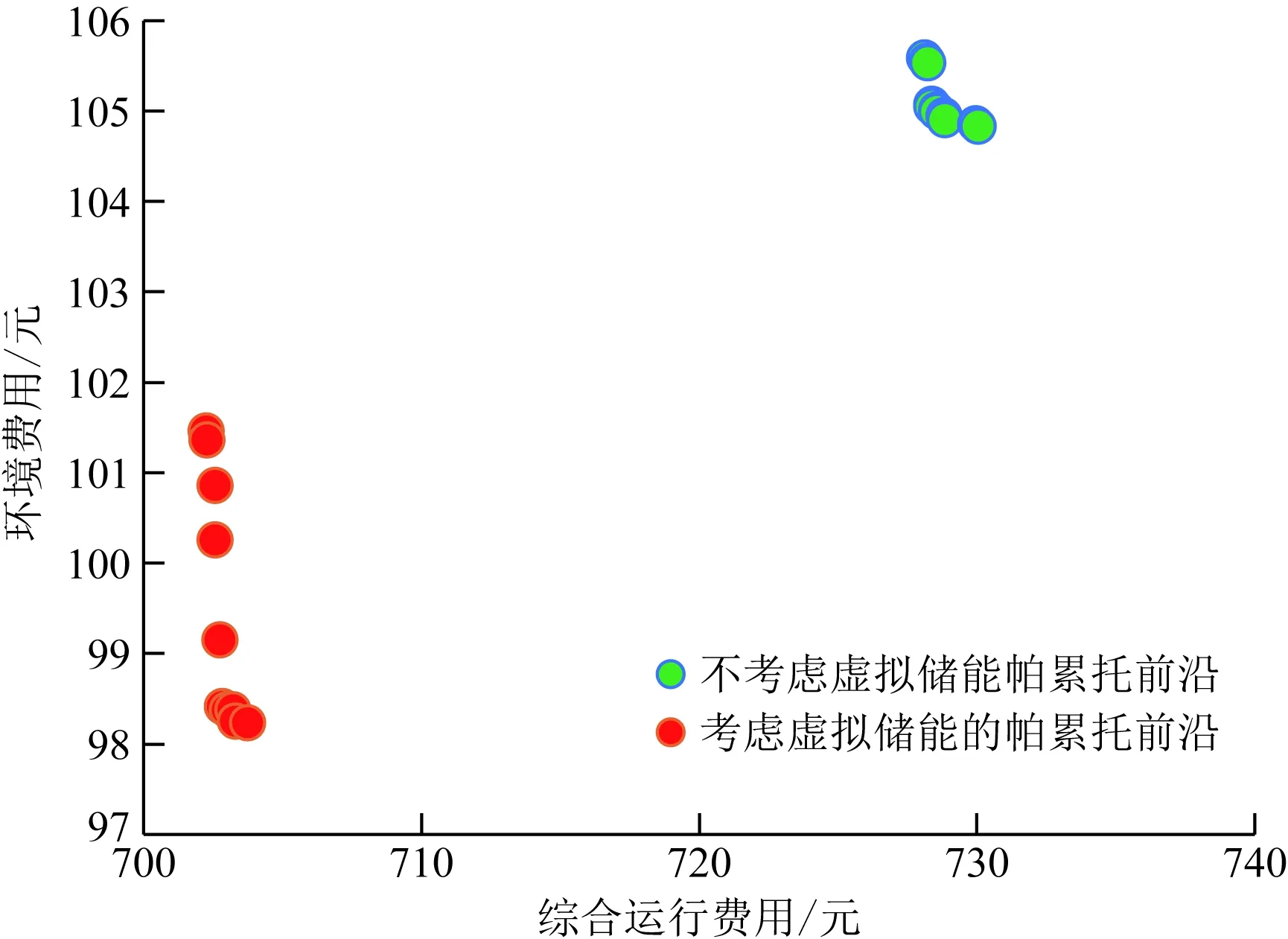
图4 帕累托前沿Fig.4 Pareto frontier

两种情况下的系统优化调度过程如图5～图7所示。

对比两种调度情况，由于室内温度的严格限制，无虚拟储能情况下的燃气发电在系统以热定电的模式下主要随室外温度和光照强度变化。在低电价时期虚拟储能参与调度时为了降低燃气费用燃气轮机出力相对较少，系统在午间的高电价时期，两类系统都会向电网售电获得收益，但是虚拟储能参与调度后可以进一步增加燃气轮机的出力从而获得更大收益，这是由于虚拟储能参与调度时会解除对室内温度的强约束，如图7虚拟储能参与后室温有较大幅度的波动，优化了建筑冷负荷曲线，在晚间的高电价时期由于光照强度的下降，系统冷负荷需求大量减少导致燃气轮机发电量不足，不足部分电力需要向电网购买，虚拟储能参与调度进一步降低了系统在该时间段的购电量，使该时段的购电成本下降。

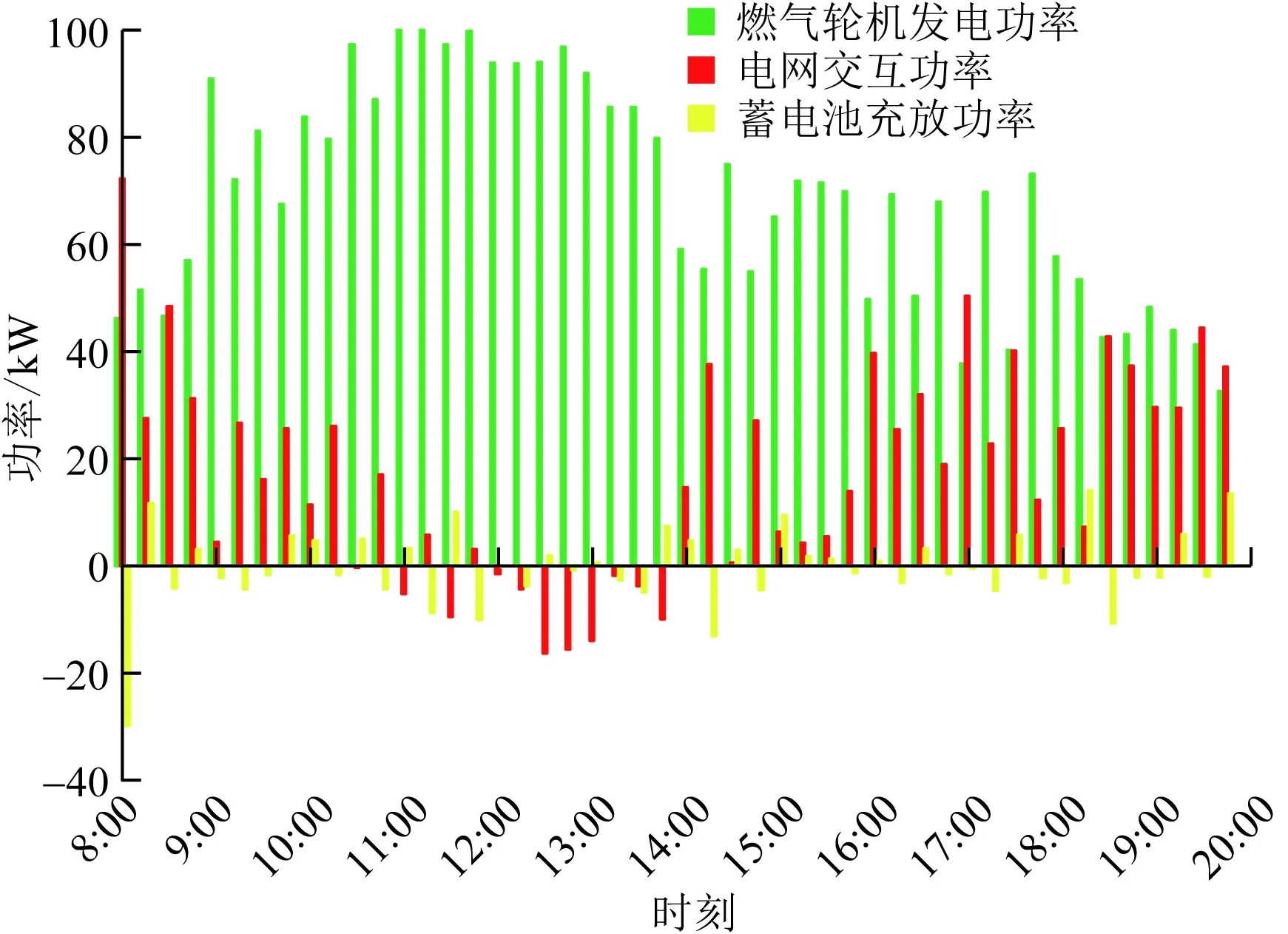
图5 考虑虚拟储能的系统优化调度Fig.5 System optimization scheduling considering virtual energy storage

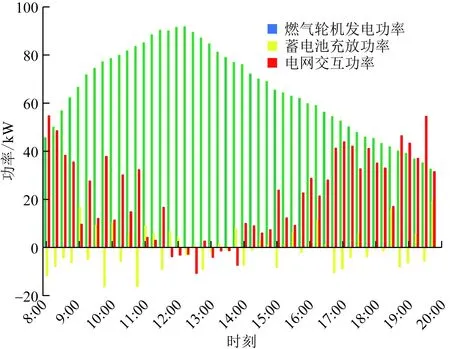
图6 不考虑虚拟储能的系统优化调度Fig.6 System optimization scheduling without virtual energy storage

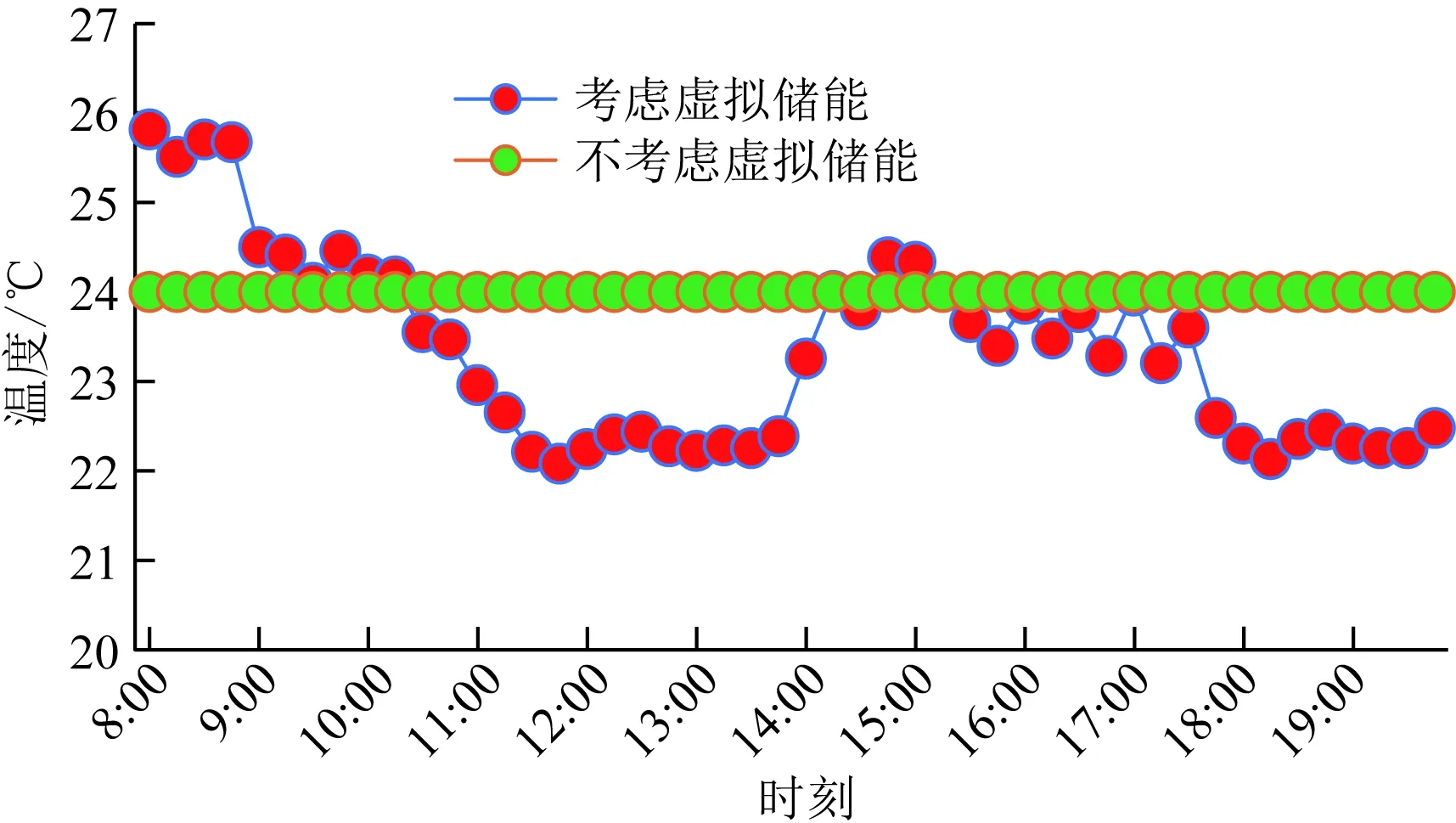
图7 室温曲线Fig.7 Room temperature curve

虚拟储能调度过程如图8所示，可以看出，建筑虚拟储能在低谷电价时期荷电状态总体维持较低水平，在高电价时期荷电状态维持在较高水平，说明了虚拟储能的充放过程可以较好地跟随电价变化来达到降低系统综合成本的目的。

系统购售电及制冷情况如图9和图10所示，可以看出，低电价时期由于购电成本较低所以两种调度情况无明显区别，在整个平价时期，购电量(模式1相比模式2)下降幅度约为13.7%，整个高电价时期购电幅度下降约18.9%，售电情况则主要发生在午间高电价时期，模式1情况下的售电为81.730 kW，模式2情况下售电为34.618 kW,上升幅度约136%。另外，在不考虑建筑虚拟储能时的建筑总冷负荷需求约为4 527.468 kW,考虑时约为4 785.624 kW,即模式1增幅约为5.7%。由数据结果可知虚拟储能参与后建筑冷负荷需求以较小幅度增大，但是对系统购售电情况带来了较大优势，表4则详细统计了两种调度模式下的费用情况。

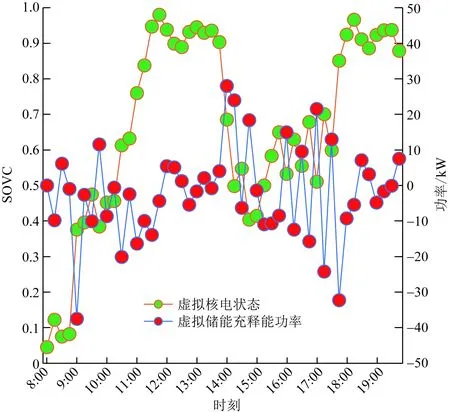
图8 虚拟储能的出力情况Fig.8 The output of virtual energy storage

由表4的费用统计情况可知，在模式1的调度情况下，环境费用相比模式2下降了约6.9%，整个调度过程总费用下降了约3.8%，说明虚拟储能参与调度对降低系统运行费用，控制环境污染具有积极意义。

图9 购售电情况Fig.9 Purchase and sale of electricity

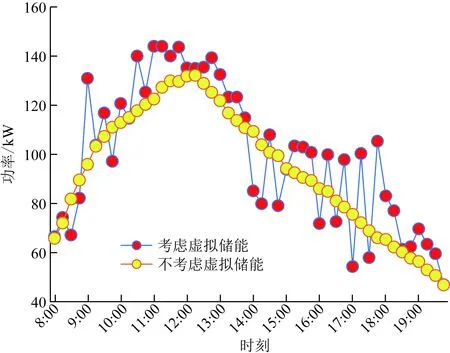
图10 冷负荷需求对比Fig.10 Comparison of cooling load demand

表4 费用统计表Table 4 Fee statistics table

4 结论

建立了建筑虚拟储能模型并引入分布式能源系统优化调度中，通过调度分析说明了虚拟储能策略参与的有效性，所得结论如下。

(1)多目标优化过程说明了单一追求综合运行费用的下降会带来环境费用的增大，所以考虑环境因素的优化调度更有实际意义，同时虚拟储能的引入与调控对于降低污染物的排放和环境保护具有积极作用。

(2)根据购售电情况和燃气轮机调度情况可知，建筑虚拟储能可以提高系统燃气轮机的灵活性，降低系统对电网的依赖程度。

(3)建筑虚拟储能在参与系统优化调度过程中，可以根据电价情况优化建筑的冷负荷曲线，降低系统运行费用，从而提高系统的经济性。