改进BP神经网络的并网逆变器分数阶比例-积分-微分控制策略

吴亚雄， 杨旭红*， 方浩旭， 张苏捷

(1. 上海电力大学自动化工程学院， 上海 200090； 2. 国网上海市浦东供电公司， 上海 200122)

在可再生能源装机容量逐年上升的背景下，并网逆变器是连接电网与可再生能源之间的关键一环，其拓扑结构与控制策略被广泛地研究与探讨。从最初的开环控制策略到现如今的比例谐振(proportional resonance，PR)控制、模型预测控制器(model predictive control，MPC)控制等[1]，控制策略也在不断地完善和改进。在光伏、风电等新能源发电系统中，由于天气等因素无法准确确定，时常存在电网电压严重偏离额定值、电网电压畸变率高等未知因素。因此给逆变器并网带来了很大的问题。如何在现有逆变器拓扑结构下，对逆变器进行实时有效的控制，应对电网突发的扰动问题，提高逆变器的鲁棒性和响应快速性[2]亟待解决。

采用PI控制时，固定的PI参数不能满足系统对于性能的要求[3]，并且其整定方法大多采用以往经验进行调试，对于电网这个大系统而言，其状态模型时刻发生着改变，无法根据状态空间方程得到精确的PI最优解。而智能算法控制对于没有精确模型的被控对象，当有外加扰动出现时，也能够通过自调节控制器参数，维持系统稳定状态，提高系统的抗干扰性能[4]。

文献[5-6]在PID基础上提出了自适应比例谐振微分(proportional resonance differential，PRD)控制方法,实现了对参考信号的零稳态误差跟踪，但由于PR控制引入了频率这一变量，需要结合系统的稳态误差综合考虑其鲁棒性能。文献[7]采用单神经元，通过设置有监督的学习规律整定PID控制参数，能够实现T型三电平逆变器良好的动态响应能力。文献[8]通过BP神经网络在线整定PID参数，实现单相光伏并网逆变器的有效并网。文献[9]通过神经网络算法整定电流环中准PR算法的参数，提升了系统的响应速度和抗干扰性。文献[10]提出了改进型的重复控制算法并应用在内环控制上，将比例积分控制看作被控系统的一部分，在此基础上加入重复控制，实现了对参考电流的快速响应。在系统模型中增加比例积分环节再进行控制，引入了一个在原点处的极点，增加了系统的不稳定性。文献[11]通过串联陷波器增加系统的阻尼，在不增加系统复杂程度的情况下，结合PR控制器，提高并网波形。但串联陷波器需要额外的设备，实现起来复杂。

基于此，现首先对三相并网逆变器控制回路进行设计，采用在滤波器电容端串联虚拟电阻避免谐振的出现，以分数阶PID控制器控制电流外环，使内环输出电流始终稳定在参考值。针对分数阶PID需要整定的参数多并且参数整定困难这一问题，采用改进BP神经网络进行自适应调整参数，以求解得到最优的参数值。通过仿真，与PI控制进行对比，验证该控制算法的适用性和鲁棒性。

1 三相LCL并网逆变器控制系统

三相LCL并网逆变器如图1所示。变换器采用三相电压型逆变器(S1～S6)，滤波环节为LCL输出滤波器(L1、L2)以实现电压的平滑并网。

为了方便设计控制策略，提出两个前提假设：①相电网电压平衡；②电感电容为理想元器件。

低频段LCL滤波器的速率衰减为-20 dB/dec；高频段的速率衰减为-60 dB/dec[12]。采用电容串联型的并网逆变器控制结构[13]，能够避免谐振尖峰的发生。通过控制算法获得一个虚拟电阻代替实际的电阻，在增大整个系统阻尼的同时避免了额外的功率损耗。如图2所示为控制流程图[14]。

检测得到电容端的电流并将其经过微分控制环节后并入逆变器内环的参考输入电流环节上，从而虚拟出一个电阻，此时电流内环参考电流为

(1)

引入了虚拟电阻，在电容端串联的电阻用虚拟电阻来替代以避免系统发生谐振，增强系统的稳定性[15]。图3为系统控制流程图，由此得出双闭环系统的开环传递函数。

Udc为直流电源；C为直流侧滤波电容；S1～S6为三相电压型逆变器；L1、L2为LCL型输出滤波器滤波电感；Cf为滤波电容；i1为逆变侧输出电流；i2为并网电流；ic为滤波电容支路电容;Ug为电网相电压有效值图1 三相LCL并网逆变器拓扑图Fig.1 Topology of three-phase LCL grid-connected inverter

为电流内环的参考电流；Rf为虚拟电阻阻值；s为拉氏变化图2 虚拟电阻滤波器框图Fig.2 Block diagram of virtual resistance filter

为给定的并网电流值；Gpiλdμ(s)为电感电流外环的分数阶PID控制器；Uin为逆变器输出端相电压；Uc为滤波器电容端电压；Gc为电容电流内环的比例控制器；G1(s)、G2(s)、G3(s)分别为滤波器状态空间模型，G1(s)=1/(L1s+R1),G2(s)=1/Cfs，G2(s)=1/(L2s+R2)图3 双闭环逆变器控制原理框图Fig.3 Control principle block diagram of double closed loop inverter

2 分数阶PID控制器

分数阶PID控制器的结构图如图4所示。

r(t)为系统的输入；Kp、Iλ、Dμ分别为比例环节、积分环节、微分环节；e(t)为控制器输出；y(t)为系统输出图4 分数阶PID控制原理框图Fig.4 Principle block diagram of fractional order PID control

分数阶PID引入了分数阶微积分，在控制状态空间中，由原来的4个点扩展到了一个面。当被控系统参数发生变化时，分数阶PID控制器仍然能够对系统进行有效的控制，比传统PID具有更强的鲁棒性更广的适应性[16]。分数阶PID控制的传递函数为

(2)

式(2)中：λ为积分阶次，0<λ；μ为微分阶次，μ<2；Kp、Ki、Kd分别为比例、积分、微分系数；R(s)、E(s)分别为r(t)、e(t)经过拉普拉斯变换后的结果。

针对分数阶微积分方程的求解，采用改进型Oustaloup滤波算法，利用整数阶次微积分对分数阶微分算子进行拟合。改进的Oustaloup滤波器[17]表达式为

(3)

式(3)中：ωh为频率上限；ωb为频率下限；d、b为固定常数；γ为分数阶次。

(4)

离散化分数阶PID控制算法[17]表达式为

u(k)=KpTp+KiTi+KdTd

(5)

式(5)中：Tp为比例环节；Ti为积分环节；Td为微分环节。

(6)

式(6)中：h为仿真步长；aj、bi为每次迭代结果的中间变量，a0=b0=1。

3 改进神经网络分数阶PID控制器

(7)

式(7)可以展开为

(8)

式(7)中：

(9)

(10)

(11)

ψ′(x)=2ψ(x)[1-ψ(x)]

(12)

同理调整隐含层权值的表达式为

(13)

式(13)中:η为学习速率;α为惯性系数。

惯性系数和学习速率的选取对控制对象产生较大的影响，固定惯性系数和学习速率的控制器在控制过程中容易出现超调量大，存在振荡问题。根据误差变化的趋势对惯性系数和学习速率进行整定。当误差Δe(k)>0时，误差曲线存在上升的趋势，说明存在控制器输出超调或输出远离期望等现象，应当减小两个系数的值;当连续误差比值减小时，说明存在响应慢或者输出正在接近被控对象期望值，为进一步保证控制结果不出现急剧变化，需要对学习速率η和惯性系数α做出调整，适当增大两个系数使曲线继续保持这种变化趋势;当Δe(k)=Δe(k-1)=0，说明系统输出已经稳定。

当|Δe(k)/Δe(k-1)|>1时，

(14)

当|Δe(k)/Δe(k-1)|<1时，

(15)

式中：α0、η0为惯性系数系数α和学习速率η的初值，取值为α0=η0=1；系数K0的取值范围一般为[-1,1]，经过多次试验，选取K0=0.5最合适。

4 仿真结果分析

将分数阶PID控制器应用在三相并网逆变器中,用BP神经网络算法对控制器中所含的5个参数进行寻优，仿真模型的参数如表1所示。

将改进BP分数阶PID控制与传统PI控制方法进行对比，在系统的稳态性能和瞬态性能两方面综合考虑评估。在瞬态情况下，使输入端的参考电流从10 A突变至15 A。仿真结果主要由两种控制方法在相同条件下的并网电压、并网电流，两种不同控制方法下的输出相电流与参考电流的波形跟踪及谐波畸变率进行对比得出，结果如图5所示。可以看出，在BP分数阶PID控制作用下，三相并网点电压Uabc为平衡的三相正弦电压，采用BP分数阶PID控制下的并网电压波形情况，三相电压的相位和幅值均保持一致。

表1 LCL并网逆变器参数Table 1 LCL grid connected inverter parameters

由图6可知，开始输入电流为10 A时，系统有功功率振荡峰峰值为42 W，振荡幅度不明显；当输入突变为15 A时，系统振荡现象加剧，有功功率峰峰值为103 W，此时系统仍处于稳定状态。

不同控制下电流突增仿真波形如图7和图8所示。由图7可知，改进BP分数阶PID控制下参考电流在0.1 s从10 A突增至15 A时，经过0.05 s电流恢复稳定，幅值为15 A。由图8可知，传统PI控制下需要0.1 s左右的时间才能够稳定，并且伴随有一定的超调。改进BP分数阶PID控制下电流突变时系统能够更快速地恢复稳定，因此采用改进BP分数阶PID控制器，提高了并网逆变器动态响应。

由图9和图10可知，在改进BP分数阶PID控制下，入网电流总谐波畸变率(total harmonic distortion, THD)为0.76%，与传统PI控制进行对比，下降了约1%，但引入了其他频率的高次谐波。

图5 BP分数阶PID控制下的并网电压Fig.5 Grid connected voltage under BP fractional-order PID control

图6 有功功率仿真结果Fig.6 Active power simulation results

图7 BP分数阶PID控制下的并网电流Fig.7 Grid connected current under BP fractional order PID control

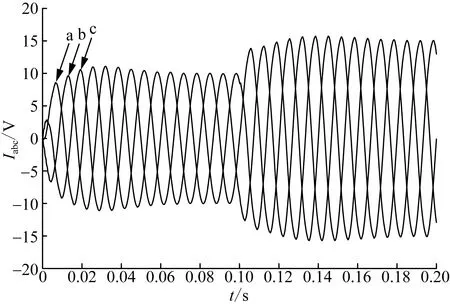
图8 PI控制下的并网电流Fig.8 Grid connected current under PI control

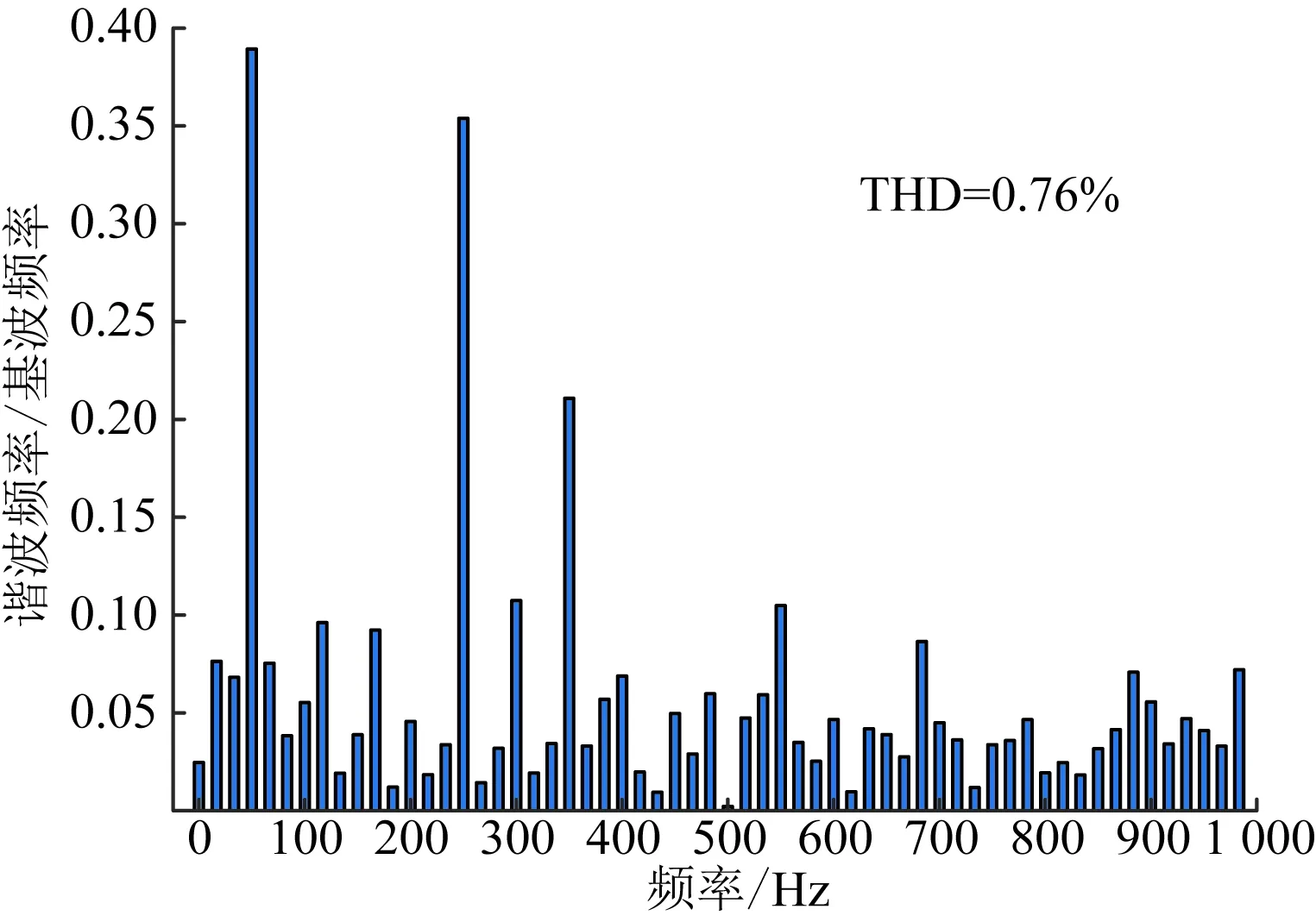
图9 BP分数阶PID控制下的THD值Fig.9 THD value under BP fractional order PID control

图10 PI控制下的THD值Fig.10 THD value under PI control

综上，证明改进的控制能够良好地跟踪参考电流变化，满足并网的要求。

5 RT-LAB硬件在回路仿真

分数阶PID控制的LCL并网逆变器系统在RT-LAB仿真平台进行硬件在回路仿真，系统参数与在Simulink仿真模型中所设置的一致。图11为当指令电流发生突变时三相并网点电流的波形。有功参考电流从10 A突变至15 A时，系统在0.1 s处发生振荡，经过分数阶PID控制使系统重新保持稳定状态。系统重回稳定状态所需时间小，且电流的波形质量高。

由颜宁等[19]通过实验验证证明RT-LAB在电力系统仿真中的可靠性，并指出其能够实时仿真要求较高的微电网系统的控制算法。图12为系统的实物实验图，采用的仿真平台为OP8665型RT-LAB。

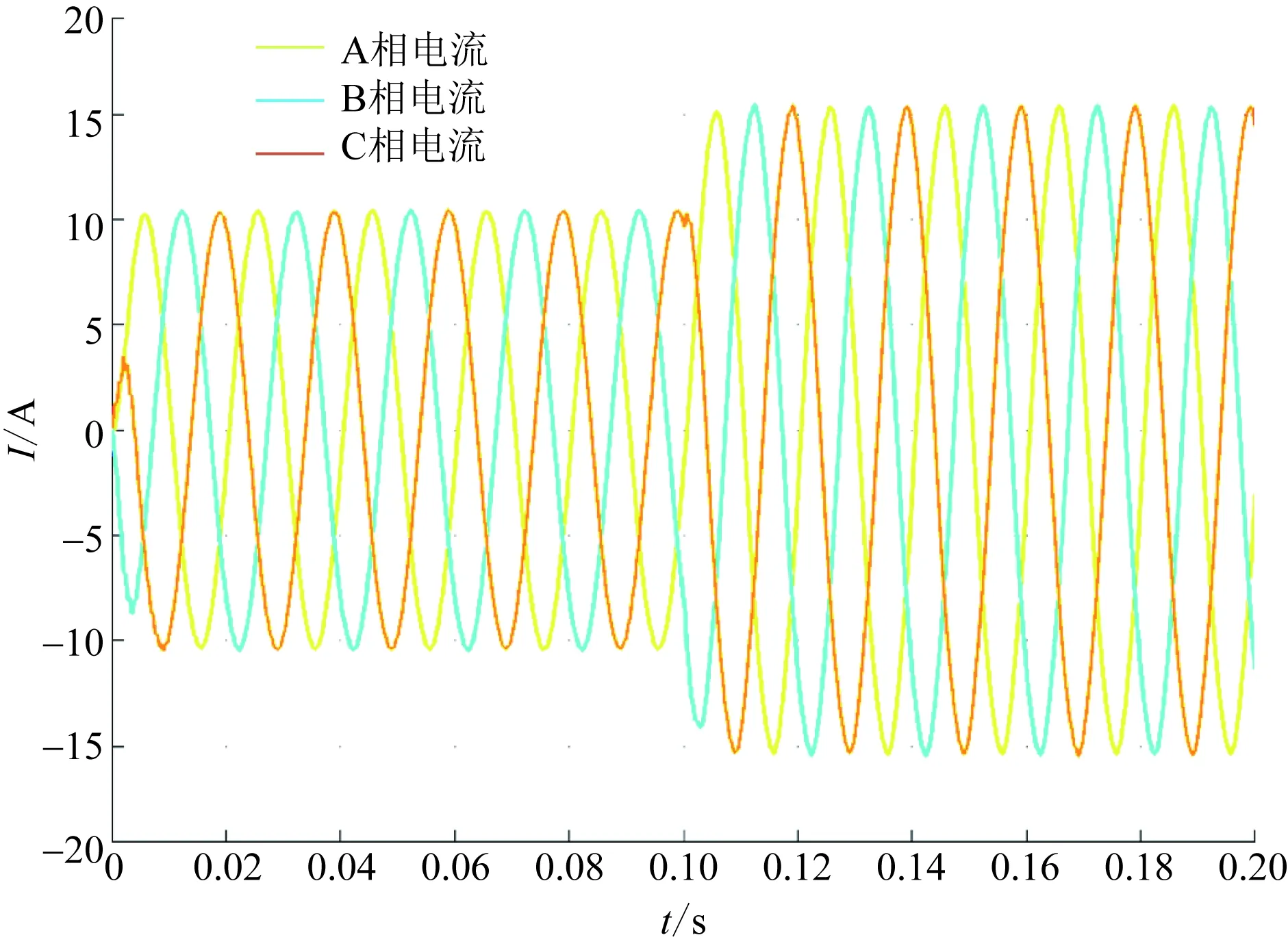
图11 电流突变时并网电流波形Fig.11 Grid connected current waveform in case of sudden current change

图12 系统实物图Fig.12 System physical map

6 结论

对新能源并网三相电压型逆变器双电流闭环控制的问题，设计了分数阶PID控制的双闭环控制策略。详细分析了BP神经网络中采用梯度下降法修改神经网络的权值原理，采用可变的学习速率与惯性系数，对系统的响应速度更快。将改进的BP分数阶PID与并网电流反馈和电容电流反馈双闭环控制相结合，得到以下结论。

(1)该控制方法不仅保留了传统PID控制易于实现和静态性能的良好优点，还可以有效跟踪电流的变化，动态性能良好。

(2)入网电流THD值下降到标准规定的5%以下，且当参考电流输入发生变化时，仍能保持入网电流THD值符合标准，并且响应速度快。

(3)采用改进BP神经网络整定分数阶PID参数的控制方法，具有良好的响应速度和抗干扰能力，仿真结果进一步证明了所提控制策略的优良性能。