地铁车站主体结构地震响应数值模拟分析

2022-06-14高文宪

低温建筑技术 2022年4期

高文宪

（中铁三局集团第四工程有限公司，北京 102300）

0 引言

地震是一种常见的自然灾害，发生时常常会给人们的生命生活，经济财产等带来严重的破坏。近年来，随着我国经济的迅猛发展，生活质量日益提高，为了真正实现可持续发展战略，必须充分利用地下的资源，来为人类造福，达到以人为本。目前地下铁道，地下商城等基础设施已经应运而生，并且呈飞速递增的趋势，确实带来了便利，也节约了土地，尤其在北京、上海、广州等各大城市发展极为显著，未来几年内定会在全国掀起地下空间开发利用的热潮。然而，最近地震的频频出现，也给我们带来了很大的障碍。地下结构投资大，假如一旦遭受破坏，其损失不可估量［1-5］。

谷音等［6］基于某大型地铁车站，利用大型通用有限元ABAQUS软件建立了考虑土-结构动力相互作用的三维有限元整体计算模型。刘晶波等［7］提出一种适用于复杂断面地下结构地震反应分析的整体式反应位移法，结合实际工程与动力时程方法进行对比研究。陈苏等［8］开展了近、远场地震动作用下可液化场地上三拱立柱式地铁地下车站结构大型振动台模型试验。杜修力等［9］基于大开地铁车站三维非线性数值分析模型，系统阐述了大开地铁车站的地震破坏机理和失效模式。

文中以沈阳地铁某车站为工程背景，应用有限元计算软件Midas-GTS，对车站主体结构进行三维数值模拟。研究沈阳地铁某车站在地震作用下，地铁车站结构受到的地震力响应。为沈阳地区地铁车站抗震研究及工程应用提供科学的参考依据。

1 工程概况

沈阳地铁某车站为地下双层三跨矩形钢筋混凝土框架结构岛式站台车站，采用两端盖挖法、中间新型暗挖法施工。根据车站岩土工程详细勘察报告，在具体的有限元建模时，沿深度变化不大的土层或者土层厚度较小的两层或多层土进行简化，各参数取其平均值，土层本构模型采用常见的屈服准则，各土层参数见表1。

表1 土层物理力学参数

车站结构的梁、板、柱、墙单元采用线弹性本构关系，计算中需给定结构弹性模量、泊松比以及重度值，混凝土结构动弹性模量取静弹性模量的1.2倍。表2为梁、柱结构力学参数。

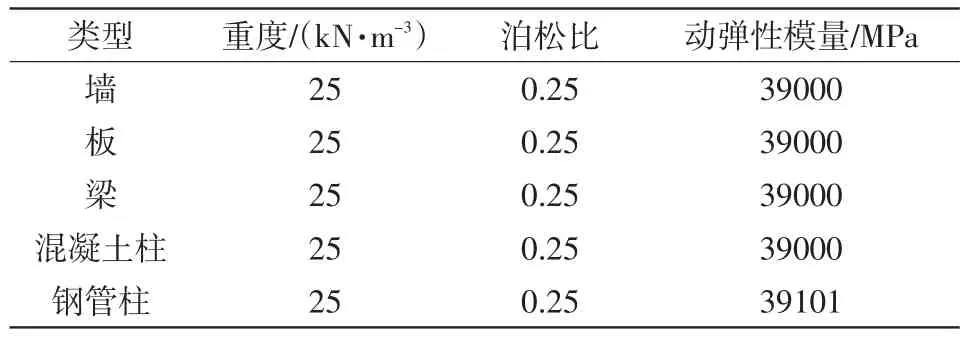
表2 梁、柱结构力学参数

2 有限元数值模拟

2.1 模型动力参数选取

针对沈阳地铁某车站主体结构采用有限元软件Midas-GTS进行动力时程分析，由于车站整体结构形式不规则，考虑到地下车站结构开挖的空间效应，现采用三维计算分析模型。计算模型的上边界取至地表，下边界取至等效基岩面，模型底部固定，计算模型的长×宽×高=226m×80m×36m，有30638个单元，11156个节点。土层采用实体单元，车站结构梁、柱采用一维2节点梁单元，板、墙采用二维4节点板单元［10，11］。衬砌结构本构模型采用弹性模型［12］。

在早期的Midas-GTS软件的计算分析中，瑞利型阻尼只能针对所计算的模型整体设置一个固定的阻尼比，而最新的2015版本中，可针对不同的材料设置不同的阻尼比，因而文中将钢筋混凝土和土体的阻尼比分别设为0.5和0.05［13］。建立的车站三维有限元模型见图1～图3。

图1 计算模型（岩土）

图2 梁、板、柱模型

图3 墙体模型

2.2 地震波的输入

文中选取ElCentro地震波开展地震响应分析。地震波加载时长为30s，加载时步长为0.04s，输出750步。根据沈阳地铁场地地震安全性评价，沈阳地铁车站 50 年超越概率2%的地震动峰值为0.382g［14，15］。图4为ElCentro波加速度时程曲线及傅里叶幅值。

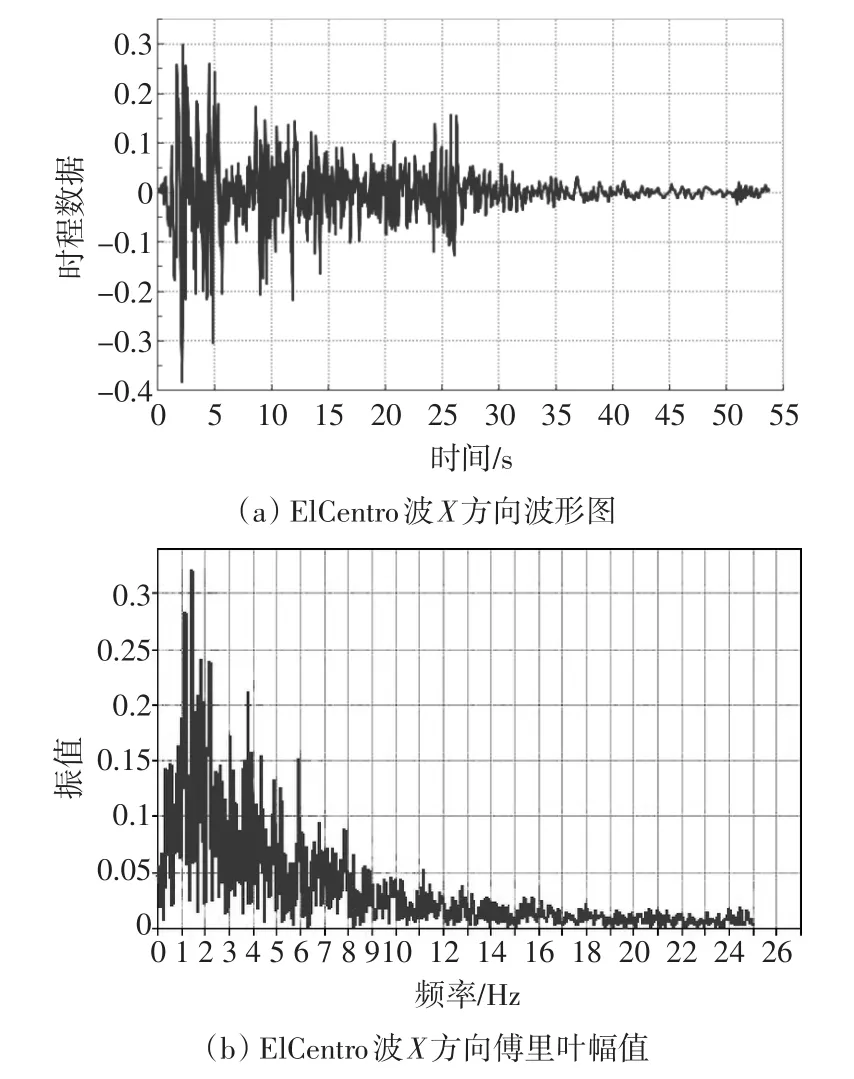
图4 ElCentro波加速度时程曲线及傅里叶幅值

3 动力时程结果分析

考虑到时程分析数据结果庞大，提取关键截面的位移值与内力值对全车站进行时程分析。图5为车站梁、柱绝对位移云图。

图5 梁、柱绝对位移

通过云图可以看出，车站梁、柱的绝对位移左边稍大，绝对位移较大位置多出现在柱顶。选取关键截面进行相对位移时程分析，定义纵向相对位移为将车站结构各部位与底板的水平纵向位移差值。关键截面有中间柱子柱顶、左边边柱柱顶、中间梁跨中截面、左边边墙顶端。图6～图9为中间柱柱顶、左边边柱柱顶、中间梁跨中截面和左边边墙顶端的纵向相对位移时程曲线。

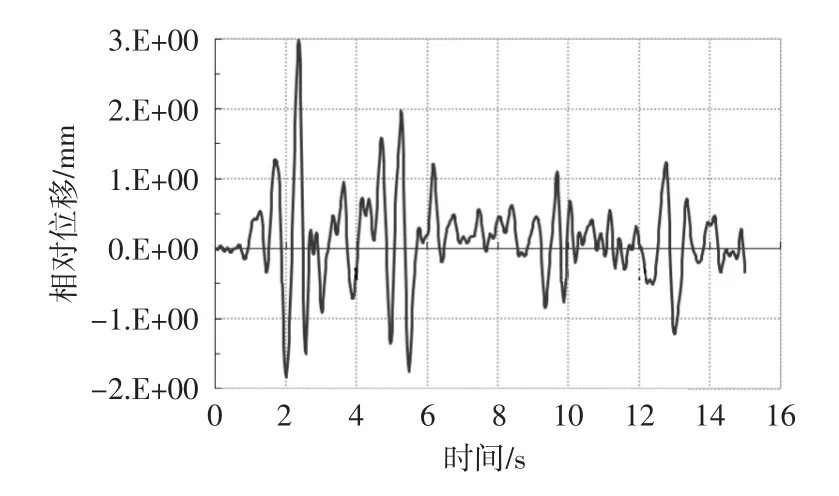
图6 中间柱柱顶纵向位移

图7 左边边柱柱顶纵向位移

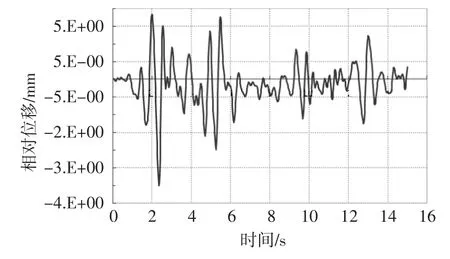
图8 中跨跨中纵向位移

图9 左边边墙顶端纵向位移

对比各个截面的纵向相对位移时程曲线，在时间为2s左右时，截面的纵向相对位移较大，与地震波最大加速度时间一致。位移峰值基本不会发生在波的后半程加速逐渐减小的过程中。

3.1 加速度时程分析结果

图10～图13给出了调幅后的ElCentro地震波车站各关键节点的水平加速度时程曲线。

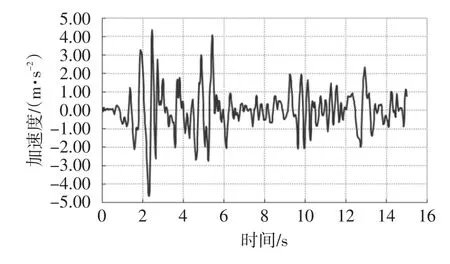
图10 中柱柱顶节点加速度时程曲线

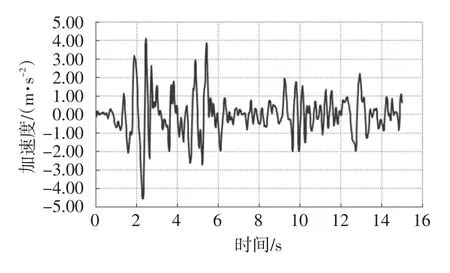
图11 中柱柱中节点加速度时程曲线

图12 中柱柱底节点加速度时程曲线

图13 边柱柱顶节点加速度时程曲线

比较中柱柱顶、柱中、柱底和边柱柱顶节点的加速度时程曲线，曲线形状相似，加速度最大值均出现在2.2s左右。其中边柱柱顶的加速度值峰值最大为4.47974m/s2，中柱柱顶节点的峰值加速度比柱中大，而柱中节点的峰值加速度又大于柱底。由此看来，在调幅后的ElCentro地震波作用下，车站节点的加速度峰值大小可能与节点高度有关。车站梁、柱加速度云图为图14所示。

图14 车站梁、柱加速度云图

从图14中可以看出，车站顶部加速度最大，中部次之，底部最小。车站两端加速度略大于中间，左端略大于右端。在调幅后的ElCentro地震波作用下，车站梁、柱的最大加速度为4.336m/s2，最小为3.335m/s2。

3.2 应力时程分析结果

图15～图18给出了地震波作用下车站各关键截面应力的时程分析曲线。

图15 中间柱子柱顶组合应力时程曲线

图16 左边边柱柱顶组合应力时程曲线

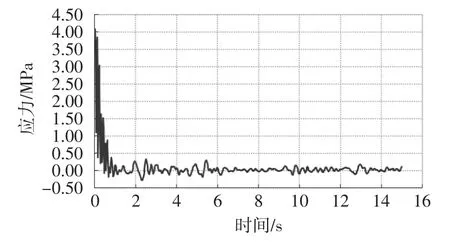
图17 中跨跨中组合应力时程曲线

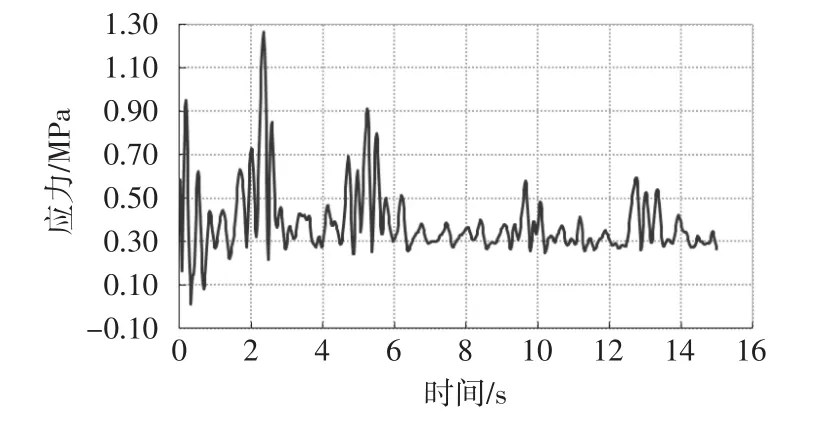
图18 左边边墙组合应力曲线

比较各个关键截面的组合应力时程曲线，发现中间柱子组合应力最大。中间柱子承受自重及地震荷载较大而截面面积较小。中间柱子柱顶、左边柱子柱顶、中跨跨中柱顶的最大组合应力均出现在0～1s之间，而左边边墙的最大组合应力出现在2s之后，可能是对于地下结构的四周均受到土体的约束作用，相当于嵌固在土体中的厚壁混凝土箱体，在地震荷载的作用下，其位移形式与周围土体保持一致，即随着周围土体的运动而运动。而左边边墙相对于以上的其他监测点处于贴近土体的位置，其动力响应受到周围土体特性及土-结构相互作用的影响更大。

地铁车站梁、柱在地震荷载作用下的组合应力云图为图19所示。