基于SEIR模型对接种新冠病毒疫苗的预测与控制*

叶红霞，刘应辉，吴凌逸

（安徽财经大学）

0 引言

2020 年元月，新型冠状感染病毒首先在中国武汉被发现，该传染病因中国春节大学生及工作人员返乡过节得到迅速传播并肆虐全中国，严重威胁人民群众的生命安全，随后的时间内，又席卷全球，严重影响了全球的经济发展［1］.疫情之初中国政府采取了强有力的措施，有效地控制了疫情的发展.其他国家，也都相应采取了一系列措施，疫情发展各不相同.中国疫情得到较早地控制以后，经济呈现出稳步增长的趋势.经过科学家们的日夜辛劳，中国在2021 年上半年成功地研制出了新冠疫苗.中国政府为巩固经济增长，保障国内外的双循环，建立全面的免疫保障机制，决定实施全民新冠疫苗接种的措施［2］.但由于现实中一些不可避免的因素的影响，使得实际疫苗接种率并不能达到百分之百.而免疫屏障的建立目前主要依靠疫苗接种，所以接种率直接影响着免疫屏障的完善程度［3］.在疫情高峰期期间，主要依靠物理隔离建立保障机制.无论是物理隔离还是疫苗接种都对社会带来了一定的利益，即使需要巨大的时间与成本，它带来的价值往往远大于前期的投入.美国作为世界上新冠疫情最严重国家，也相应采取了很多措施，它是大规模快速接种新冠疫苗的国家之一，而最近美国的疫情也有好转的趋势.随着疫苗接种率的逐渐提高，对美国的疫情也会有巨大的影响.

针对接种新冠病毒疫苗的预测与控制，该文研究主要目的在于新型冠状病毒潜伏期长，具有高隐秘性，且传播能力强，严重影响了人们的生活，就需要建立新冠病毒的免疫屏障.而接种新冠疫苗的人群感染新冠病毒的概率会大大降低.因此，接种新冠疫苗是建立免疫屏障最主要的措施，但疫苗接种率的不同也会很大程度上影响免疫屏障的构成.新冠疫苗的接种率关乎全国人民的生命安全，关系到国家与民族的前途和命运.研究疫苗接种率既对本次传染病的治疗有重要价值，也对未来防控其他传染病有重要借鉴意义.研究疫苗接种率对建立免疫屏障的影响就尤为重要.

在中国，现阶段提供免费接种新冠疫苗服务，疫苗接种人数已超过7 亿，群体免疫屏障基本已经形成，拥有有效控制新冠疫情的能力.中国科学家预测中国只要完成11 亿人次的疫苗接种工作，基本就可以实现群体免疫.除中国外，大部分国家群体免疫屏障的构成形式非常严峻，疫苗技术不够成熟，政府采用缓解政策，难以控制疫情的局势，导致疫苗接种率较低，无法有效控制疫情的走向.中国也对很多国家实行新冠疫苗的援助，对解决全球疫情问题有着重要作用［4］.

1 数据来源与假设

该文数据来源于安徽财经大学2021 数学建模暑期培训模拟赛一A 题，为了便于研究问题，提出以下假设：假设模型中“康复”的群体短时间内不会被再次感染；假设模型中无超级感染者；假设潜伏者的潜伏期长短一致；假设所有人接种新型冠状病毒疫苗后无不良反应；假设潜伏者中无直接自己痊愈群体；假设接种疫苗后不会感染接种新型冠状病毒；假设所有易感人群均为被隔离；假设新型冠状病毒不会发生突变；假设不考虑外来人群的流入和流出；假设疫苗接种后不会影响自身免疫力；假设疫苗本身有安全性、有效性等方面的保障；假设湖北省总人数不变；假设所有疫苗治愈程度相当；假设疫苗接种一次完成（两剂型疫苗间隔时间相比预测曲线的时间很短）.

2 疫苗接种率对构筑免疫屏障的影响

2.1 研究思路

为了研究疫苗接种率的控制对构筑免疫屏障的作用，需要考虑到新型冠状病毒的特征，建立新型冠状病毒的传染动力学模型.由于新冠病毒对社会的危害比较严重，许多学者在这方面做了不少工作，提供了丰富的方法.SEIR 模型是考虑到新型冠状病毒具有潜伏期，其易感者通常会先进入潜伏期，一定时间和概率会转变成感染者.因此，使用SEIR 模型并对其进行改进，以便对新型冠状病毒的传染性进行分析（如图1 所示）.

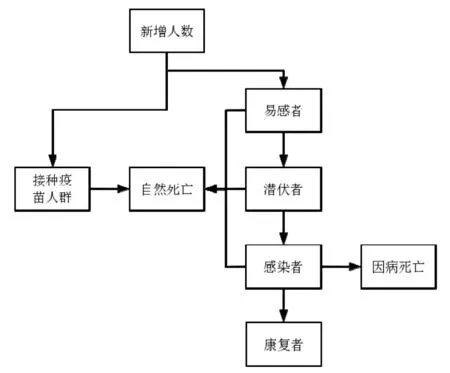
图1 研究思路图

2.2 研究方法

在单位时间内，易感者和感染者接触且被传染的强度为β，新增人数μN，由于接种疫苗的人群不会感染新型冠状病毒，故除去接种疫苗后的总人群存在易感者、潜伏者、感染者、康复者［5］，其总人群为N（1－ω），时间为t.

单位时间内由易感者S转化为已感染者I的人数为：

利用Excel处理微分方程.由于无症状感染者的传染率较低，对此数据分析意义不大，再由确定的β ≈0.048.σ ≈0.1.将易感者、潜伏者和感染者以及康复者的微分方程导入到EXCEL中.疫苗接种率ω的求解.疫苗接种率

2.3 结果分析

以下分析约束条件.从实际中可知，疫苗接种率ω越高，其感染人数I越少，即疫苗接种率与感染人数呈负相关.根据实际情况，疫苗接种率过高会导致新型冠状病毒的突变，但疫苗接种率水平较低也不会得到明显效果，所以将疫苗接种率ω控制在40% ～90%之间.由于潜伏期人群与感染人群相比较难被发现，潜伏期人群被追踪隔离［7］的概率ρ1小于感染人群被追踪隔离的概率，即ρ1＜ρ2.

接下研究易感者与潜伏期人群或感染人群的接触速率.知道新型冠状病毒的传染性很强［5］，一旦易感者与潜伏期人群或感染人群直接接触，很大概率会成为新的潜伏者或感染者，潜伏期人群转化为感染者的概率较低.通过查找资料和文献得知β ≈0.048，σ ≈0.1.

通过模型的建立与求解，得出如果病毒自然感染，疫情得到控制的时间将会延续到几十年；但如果一个国家的疫情控制是基于疫苗的作用，那么，疫苗的接种率至少需要达到总人群的50%以上，才会表现出明显作用；如果疫苗接种仅仅覆盖了30%的人群，那么，即使疫苗的保护率很高，也难以阻碍疫情的流行.同时，通过提高疫苗的接种率与疫苗的保护水平，新型冠状病毒的流行性水平可以迅速下降.还发现由于新型冠状病毒的传染性很强，因此，对潜伏期人群和感染者进行隔离，虽然潜伏期人群和感染人群被追踪到的概率会未被隔离的潜伏期人群和感染人群的下降而下降，但却有效防止新型冠状病毒的传播，也在很大程度上降低了总人群的感染率.物理隔离的实施也对疫情防控起到了关键性作用，增大了Ea、Ia，很大程度上减少了潜伏者和感染者，其隔离措施的付出远小于得到的收益.可通过戴口罩、勤洗手等预防措施减小易感者与潜伏期人群或感染人群的接触速率β的取值，能够一定程度上降低潜伏期人群和感染人群的数量.同时加强隔离措施也可有效降低潜伏期人群的确诊感染率σ，减少感染者的人数.

3 考虑建立群体免疫屏障的的步骤与成本

3.1 研究思路

查找中国人口官网，得到武汉2020 年的人口总数大致为N ＝12326518，再查找武汉疫情官网得到2020年1月21日到2020年6月9日的感染数据，考虑到疫情高峰期后武汉市新冠肺炎疫情得到了有效的控制，于是，选取2020 年1 月21 日到2020年3月20日的数据进行处理，并取1月21日的t ＝0，以次逐渐递增，直到3月20日的t ＝59，将t作为自变量来绘制到Excel表中.以天数为横轴，感染人数为纵轴，汇总出散点图，如图2 所示.

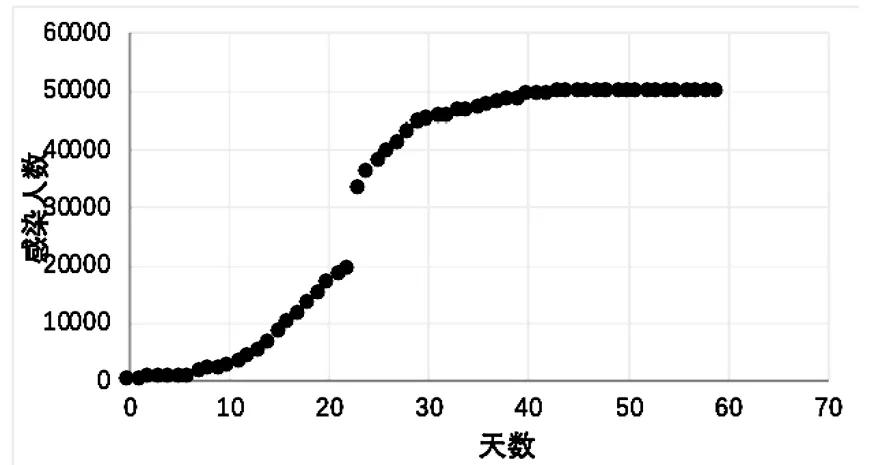
图2 武汉市感染人数的散点图

认识疫情期间感染人数的变化规律，建立相关模型，做出较准确的预报，是有效控制疫情传播的前提.Logistic 模型是对指数增长模型的基本假设进行修改后得到的，可有效预测新型冠状病毒的传播速度.通过对数据的处理后，发现利用Logistic模型比较合适.

3.2 研究方法

考虑到疫情期间的隔离人群，自身免疫等，即感染人数的阻滞作用会对武汉市感染人口增长率b产生影响，使得感染人口增长率b 随着武汉市感染人数x的增加而下降.若将b 表示为x的函数b（x），则它应是减函数［9］，即

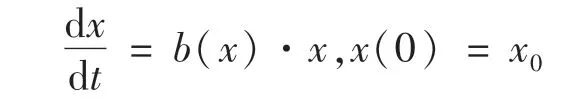
对b（x）最简单的一个假定是：设b（x）为x的一个线性函数，即

由于a、b、K的值都是未知的，需要先对其估计1个值，计算出每天的感染总人数，即x（t）.结合实际情况，可以假设a ＝10，b ＝0.2，K ＝0.01.根据此假设，可以将2 个数据的散点图放到同一个函数图像中，计算出模型中每天的感染人数.

图3 为建立参数赋值模型后得到的感染人数与天数的关系.对比图2 和图3，可以看出，建立的模型与实际情况差别很大.即a、b、K的取值不合理.所以，想要计算出a、b、K的最优解，就需要设置出一个目标函数.因此，目标函数的选取对模型该有着很大的影响.已经知道每天的实际感染人数以及计算出模型中每天的感染人数，将模型中每天的感染人数设为y，所以可以将目标函数设为：

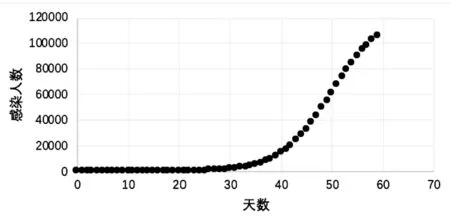
图3 参数赋值模型

该函数取最小值时的a、b、K即为最优解，由于该模型是非线性规划问题，使用EXCEL 中的solver功能进行最小值求解，将a、b、K 设为可变参数，a、b、K的值保留三位小数，求解出最终的m ＝127574747，即a、b、K的值为：

a ＝5.853，b ＝0.271，K ＝0.004（7－1）

图4 中，红线代表模型函数，可以据此直观看到从疫情开始感染人数增加缓慢，一段时间后，感染人数会大幅度增加.之后，由于采取隔离措施、疫苗接种率的提高等措施感染人数几乎不会上升.

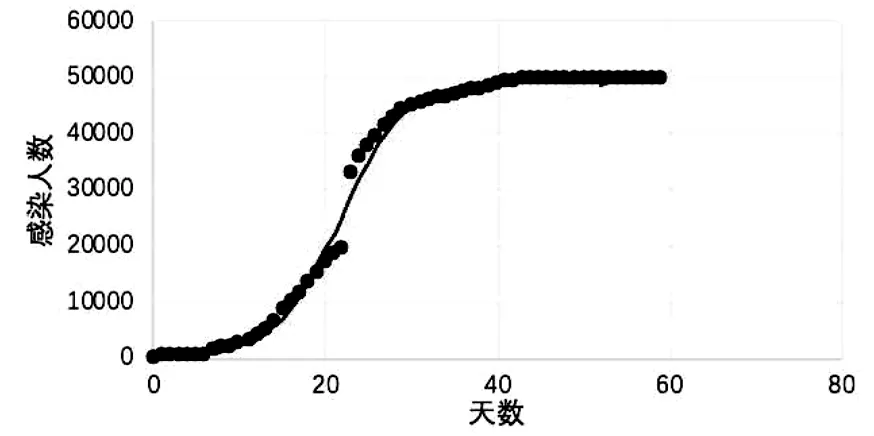
图4 Logistic模型可视化

下面，将每天的实际感染人数与模型中计算出的感染人数进行比较，可以直观的看出模型值与实际值差别.其中，图5中的点越接近y ＝x线证明模型的拟合效果越好.

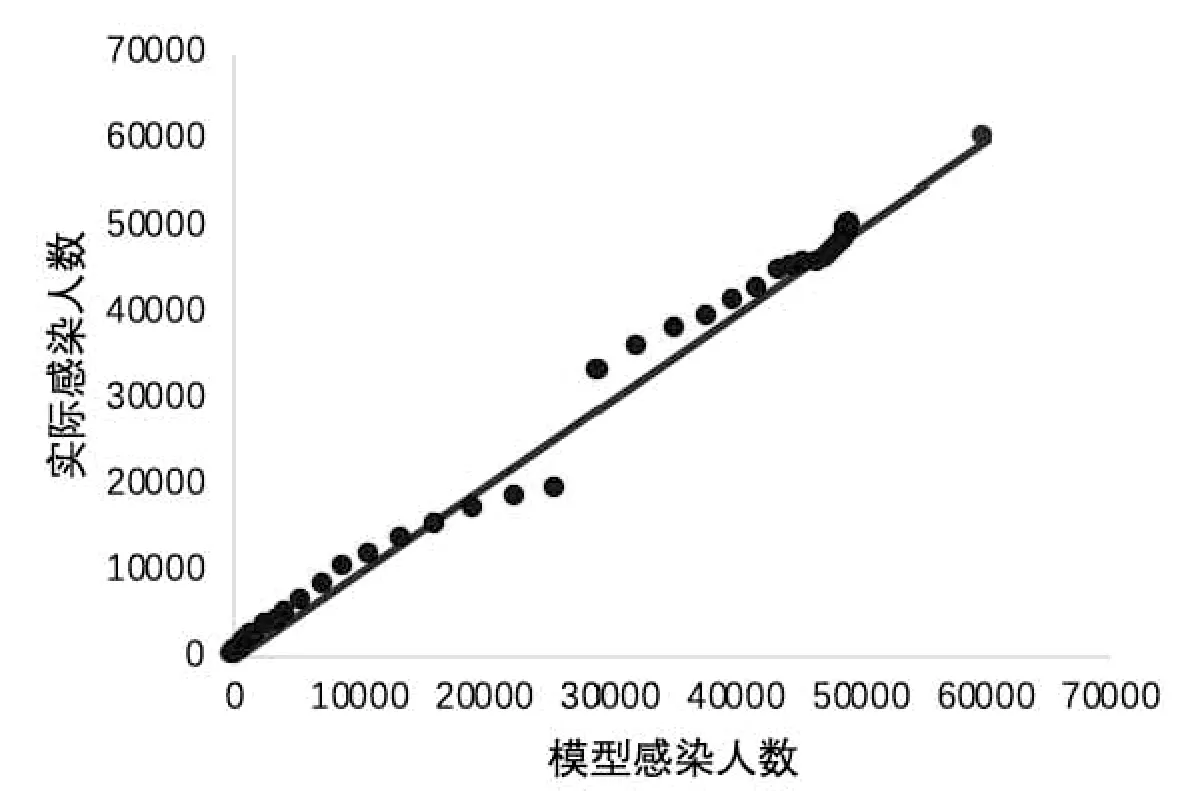
图5 模型的拟合直观图

3.3 结果分析

对于武汉市群体免疫的构建，主要通过采取隔离措施和接种疫苗来增大感染人数的阻滞作用，降低感染新冠肺炎的人数［11］.同时通过观察模型可直接预测出免疫屏障构建完成的时间.观察感染人数的变化，考虑到所有易感人群都可接种新冠疫苗，推算出免疫屏障的完成时间大约需要4 ～6 个月.免疫屏障的建立需要疫苗接种率达到60% ～70%，其接种的疫苗在近期内能够维持新冠肺炎的抗体在较高水平上，一定程度上增加了市民的疫苗的接种率.由于新冠疫苗的接种是免费的，会得到社会各界的支持，从而能够降低总成本，使得社会接种疫苗的平均成本降低.

4 分析疫苗接种对美国疫情的影响

4.1 研究思路

为了研究接种疫苗对美国疫情改变的影响，需要考虑到新型冠状病毒的特征，疫苗抑制病情发展程度以及疫苗接种对人群意识和反映的变化，建立新型冠状病毒的传染动力学模型.由于新冠病毒对社会的危害比较严重，许多学者在这方面做了不少工作，提供了丰富的方法.SEIRD模型是考虑到新型冠状病毒具有潜伏期，其易感者通常会先进入潜伏期，一定时间和概率会转变成感染者.因此，对SEIR模型进行改进，模型结合疫苗接种的影响和人群自身安全意识等额外因素，该文的模型在接种疫苗的情况下预测表明，covid－19 的未来轨迹将在很大程度上取决于人群对疾病和疫苗接种的反应行为；以便对美国疫情走向进行分析.

4.2 研究方法

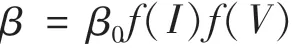
将疫苗接种视为一次性事件，在这种情况下，个人将接受一剂完整剂量的疫苗，尽管目前的某些疫苗需要两剂且必须在不同时间接种.鉴于与两剂疫苗之间的时间间隔相比，COVID－19 预测曲线的时间尺度要长得多，所以忽略两剂之间的时间间隔对接种率进行建模是合理的，而不会显著降低预测准确性.该文中的所有疫苗分布均以每天0.1%，0.3%，0.5%的三个固定比率建模，结果如图6、图7 所示.

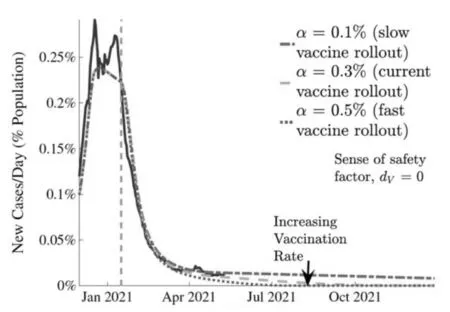
图6 dv ＝0 时，病毒患者增长速度与时间的关系

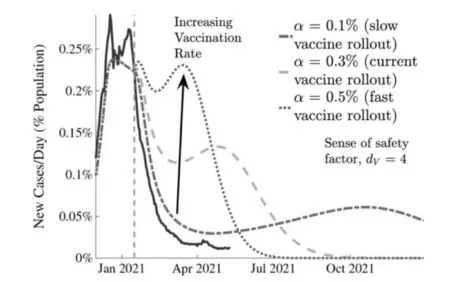
图7 dv ＝4 时，病毒患者增长速度与时间的关系

4.3 结果分析

通过建模发现，虽然疫苗的推出会更快的结束covid－19，但也存在一些情况，快速接种疫苗会给人群带来过多的安全感，这将导致感染病例在短期内大幅增加.这种安全感还可能导致地方当局政府放松限制［12］.但如果大部分人口选择不接种疫苗，这可能会造成疫情变得难以控制，美当局政府需要谨慎来预测，通过鼓励所有能够预防病毒传播的方法措施来限制任何潜在的疫情传播风险.该文的建模结果表明，在美国坚持打疫苗且防疫措施不放松的情况下，到2021 年8 月可以合理控制COVID－19 的传播.

5 结束语

该文利用SEIR 模型，根据现有数据进行计算得出完成免疫屏障需要疫苗接种率至少为多少.同时，利用Logistic 回归［13－15］得到武汉市完成免疫屏障所需时间等，最后根据SIRDV 模型推断出疫苗的接种对美国的影响.通过该文的分析，得出疫苗的接种率的高低与完成时间的长短对完成免疫屏障的建立有着很大的作用.同时，对美国而言在疫苗接种率提高的情况下，会使得部分居民的防疫意识变弱，从而导致感染率上升的异常情况的出现，但不能因此放弃疫苗的接种.在实现全民疫苗的情况下，继续坚持防疫的警惕性，疫情将在不久的未来得到控制［16］.全球的经济也将得到复苏，一切生活都将会回归正常.