冻土长期强度的衰减特征及屈服准则
2022-06-14申明德周志伟
申明德, 周志伟, 马 巍
(1.中国科学院西北生态环境资源研究院冻土工程国家重点实验室,甘肃兰州730000; 2.中国科学院大学,北京100049)
0 引言
岩土材料的强度一直以来都是工程建设的重要指标。冻土中冰的胶结作用以及冰-水相态平衡是冻土强度的核心机制,它决定了冻土具有强流变特性,表现为蠕变、应力松弛以及强度衰减等现象。冻土的强度衰减是寒区路基、桩基和人工冻结井壁在服役过程中出现病害或失稳的重要诱因[1-6]。因此,掌握和理解冻土在复杂热力条件下的强度衰减特性及其机理是保证寒区工程基础设施稳定运营、安全维护的必要前提。
应力松弛试验是研究冻土强度衰减和确定冻土长期强度的重要方法。维亚洛夫[7-8]通过蠕变-松弛耦合试验来确定冻土的长期强度,并在工程实践应用中取得了较好效果。Ladanyi 等[9]评估了三类由室内三轴松弛试验确定冻土蠕变参数和强度特性方法的可靠性。Karpenko等[4]认为多级应力松弛试验可用于确定冻土流变参数。应力松弛指冻土在恒定应变下,应力随时间的发展而降低的过程。冻土的强度衰减过程是与应力松弛相关的流变特性的工程体现[1]。维亚洛夫[7-8]认为因矿物颗粒和冰包裹体的重新定向及部分弹性变形转变成塑性变形而造成的应力松弛,是决定冻土强度性质最重要的因素;应力松弛会弱化孔隙冰与土粒间的联结作用,改变冻土的物理力学性质。国内外对复杂应力状态下冻土强度衰减的研究较少,多集中在分析冻土的松弛特性及相关的影响因素。吴紫汪等[10]将兰州黄土的单轴应力松弛过程分为强烈松弛阶段和缓慢松弛阶段,发现预应变量越大或温度越高,冻土的应力松弛越强烈,并基于大量冻土应力松弛试验结果给出了冻土的长期强度方程[11]。Cong 等[12]基于扰动状态概念研究了冻融循环对膨胀土应力松弛特性的影响,剪切应力随冻融循环次数增大而线性降低,当冻融循环次数超过7次时,该影响就不明显了。Ladanyi 等[9]的试验结果表明100~300 kPa 的围压变化对-5 ℃下冻结Ottawa 砂土的松弛特性影响并不显著。王松鹤等[13-15]在-1 ℃、0.5~3 MPa 下开展了一系列应力松弛试验,研究了预应变过程和排水条件对冻结青藏黏土松弛特性的影响,发现随着围压增长,松弛过程初期的瞬时松弛量增加,松弛稳定历时延长。
常温土(融土)的相关研究认为,岩土介质的松弛过程中应力与时间对数为线性关系,且几乎不受围压影响[16-18]。但值得注意的是,冻土的力学行为与融土相比,对围压的响应特征相差甚远。经过多年来对冻土力学行为的深入研究,许多学者认为冻土的瞬时强度随围压的增长会出现明显的三阶段特征,即快速增大、快速降低和平缓降低。这是由围压对冻土的两种影响机制(压密增强效应和冰晶压碎压融弱化效应)耦合的结果,将直接影响冻土内的结构联结作用[1,19-24]。因而从强度机制上看,冻土的流变特性必然受围压影响。另一方面,多年来随着人工冻结技术在深部地下工程建设中的广泛运用,人工冻结深凿井开挖工程深度已达到千米级[25-28]。然而,现有研究仅考察了低围压、简单应力状态下冻土的应力松弛规律,缺乏对复杂应力状态下冻土强度衰减特性的研究,已有研究的相关结论在深部地下工程中的适用性值得怀疑[29]。因此,本文基于冻结路基土在强度点处的应力松弛试验,在充分研究围压对冻土松弛特性影响的基础上,确定考虑围压影响的长期强度方程,详细分析冻土黏聚力、内摩擦角及复杂应力状态下的冻土强度在流变过程中的演化规律,建立考虑应力松弛效应的冻土率相关强度准则。
1 材料与方法
1.1 土样制备
试验所用土样为G30(连云港—霍尔果斯)高速公路兰州市榆中段路基填土,其基本物理指标及粒径分布分别见表1~2,击实试验结果见图1。土料经自然风干并去除杂质,过2 mm 土工筛后置于密封干燥处保存。采用标准刚性模具、液压制样机和自动脱模机将土料压制成直径和高度分别为61.8 mm 和125 mm 的圆柱体试样。制样干密度为1.769 g·cm-3,含水率为16%。将试样进行抽真空饱和12 h 后,放入冰箱内在-30 ℃下快速等向冻结24 h 以上。最后,将冻结后的试样置于温度为目标测试温度(-6 ℃)的恒温箱内恒温24 h。

表1 路基土的基本物理指标Table 1 Basic physical indices of the subgrade soil

表2 路基土的粒径分布Table 2 Grain size distribution of the subgrade soil
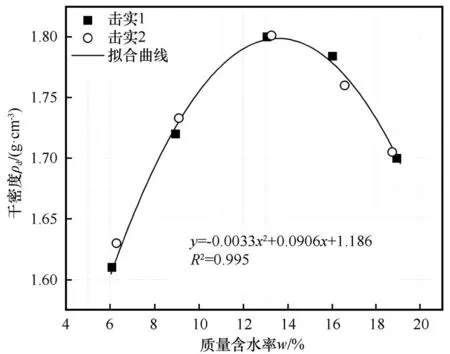
图1 路基土的击实试验结果Fig. 1 Proctor compaction test results of the subgrade soil
1.2 试验方法
冻结重塑路基土的应力松弛试验均使用MTS-810 低温三轴仪完成,该设备被广泛应用于冻土力学特性研究,其性能参数在相关研究中已被详细介绍[21-22,30],不再赘述。试验机轴力加载系统及围压系统均可由编制的加载程序独立控制。
为研究冻结路基土复杂应力状态下的冻土强度衰减特性,在0.5~16 MPa 围压,-6 ℃下进行了一系列应力松弛试验,试验方案见表3。试验前,使用循环冷浴系统将围压室内的温度恒温至-6 ℃,并利用空调系统控制整个试验过程的环境温度恒定为18 ℃,以保证试验温度稳定。随后将制备完成的试样快速放入试验机内后,排净空气使液压油充满压力室。装样完成后,恒温2 h 使液压油与试样的温度均达到稳定后开始加载程序。加载程序示意图见图2。对试样施加预定围压后开始轴向加载,以4×10-5s-1的应变率加载至轴向应变达到15%后保持轴向位移恒定,进入强度衰减阶段。试验全程自动采集轴向力、轴向位移、围压和围压位移数据。
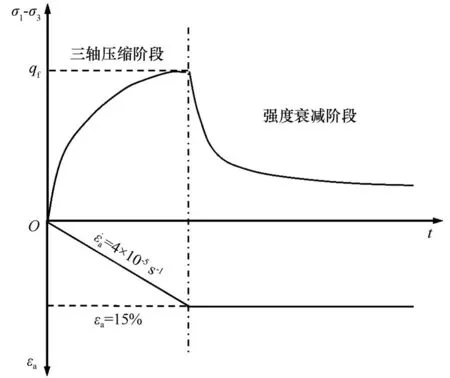
图2 加载过程示意图Fig. 2 Schematic diagram of loading procedure
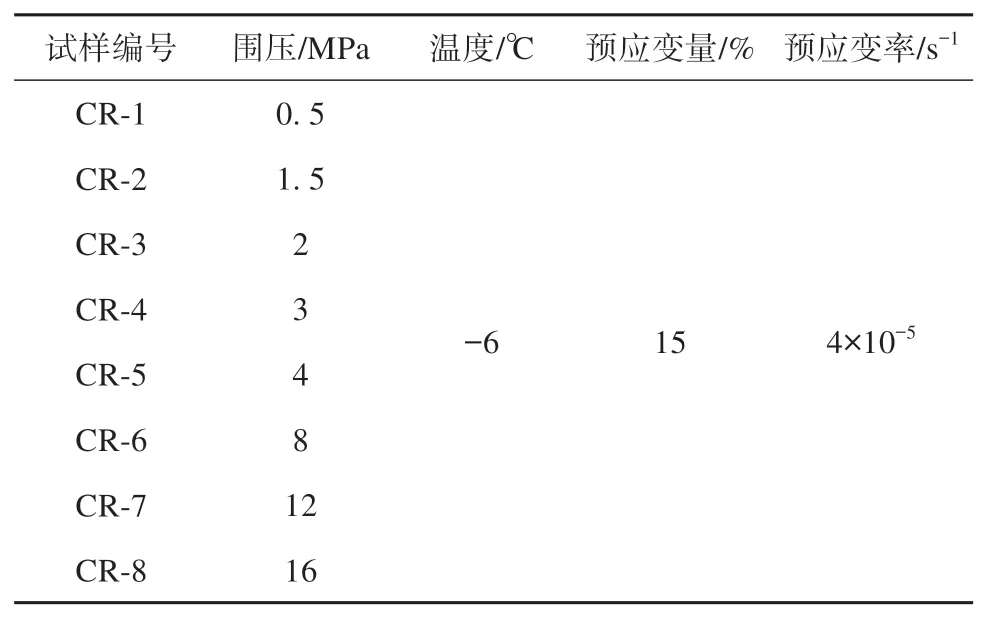
表3 应力松弛试验方案Table 3 Programs of stress relaxation test
2 结果与分析
2.1 围压对冻土松弛特性的影响
图3(a)为-6 ℃、0.5~16 MPa 围压下冻结路基土的偏应力-松弛历时曲线。试验结果表明,冻结路基土在各围压下的松弛过程均表现为典型的松弛曲线,松弛过程可分为强烈松弛阶段和缓慢松弛阶段。强烈松弛阶段出现在应力松弛初期,持续约1~2 h,随后过渡到缓慢松弛阶段。应力松弛过程可以认为是冻土内部分弹性变形转变为黏塑性变形,这一过程伴随着土体内部的能量变化[1,10]。这一变化过程和材料的抗松弛性能可以通过应力松弛率变化来反映。图3(b)为松弛应力率随松弛历时发展的变化曲线。由图3(b)可以明显地观察到,在松弛历史0~1 h 期间,应力松弛率的量级由超过1×102MPa·h-1极快地衰减至1×10-1MPa·h-1,而在后续松弛历时内,应力率的衰减量小于1×10-1MPa·h-1。在进入缓慢松弛阶段后,围压为1.5~12 MPa 时,围压对应力松弛率的影响并不明显,这与王松鹤等[14]获得的高温冻土在0.5~3 MPa的试验结果类似。围压为0.5 MPa 和16 MPa 的偏应力松弛率分别在松弛历时为21 h 和13 h 时衰减至0,而其他围压条件下则均在9 h左右稳定于0.01~0.02 MPa·h-1。可以猜想,在复杂应力状态下发生的应力松弛,可能存在一低一高两个围压阈值,当围压低于小阈值或高于大阈值时,松弛过程将较其他情况明显地更快达到稳定状态。因此在特定条件下,围压对于冻土应力松弛过程存在明显影响。
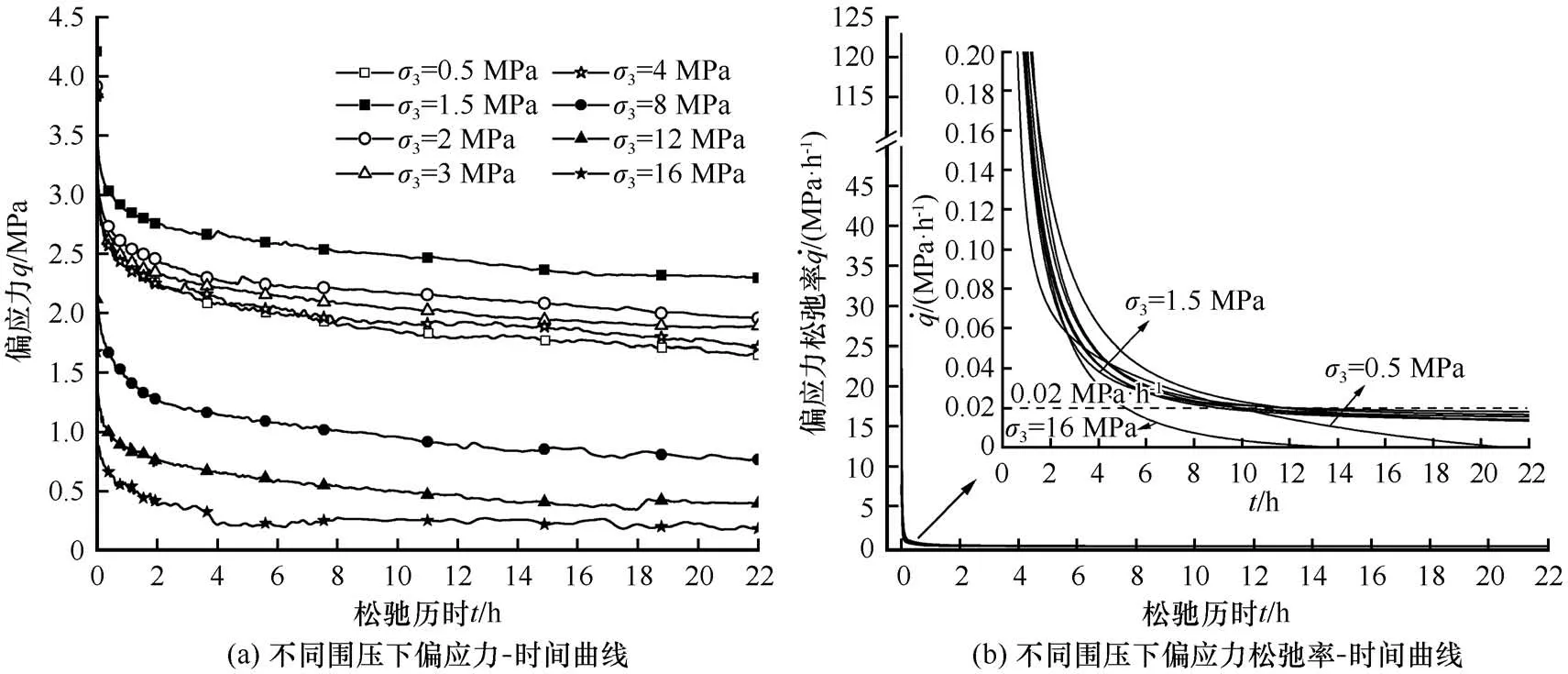
图3 松弛过程曲线Fig. 3 Curves of relaxation procedure under various confining pressures:deviator stress-time(a)and deviator stress relaxation rate-time(b)
冻土作为一种具有强流变特性的岩土材料,可通过松弛时间Tr和松弛度S来评价其松弛特性。松弛时间Tr体现了材料的流变特性,为材料的固有参数。Tr越小,材料越接近液体状态;Tr越大,材料越接近固体状态。松弛度则表征了应力松弛的强烈程度。这两个关键参数可通过图4来进行定义和求取。松弛时间Tr可由式(1)计算求取。
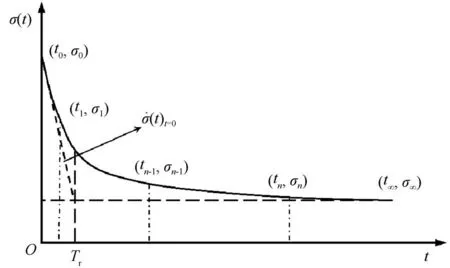
图4 松弛特性参数示意图Fig. 4 Schematic diagram of relaxation characteristic parameters

式中:σ0为松弛过程的初始应力;σ∞为稳定应力;σ̇(t)t=0为松弛曲线上t=0 处的切线斜率。松弛度由式(2)求取。

式中:σf为破坏强度。本试验预加载阶段所有曲线均为硬化型曲线,定义应变为15%处的应力为试样的破坏强度。因此,本试验中初始应力等于破坏强度。
需要指出的是,σ∞为理论上时间无限长所得到的稳定应力,松弛曲线稳定极限的判断与松弛历时t的尺度相关,在实际试验中极难获取。当进入相对稳定的缓慢松弛阶段时,松弛曲线可近似看作等斜率直线,取该段数据进行因素影响分析同样可以得到可靠的结果。因此在分析试验数据后,基于图3(b)定义当应力松弛率小于0.02 MPa·h-1时松弛曲线上对应时刻的应力作为σ∞,并据此计算各围压下冻结路基土的松弛时间和松弛度,结果如图5所示。
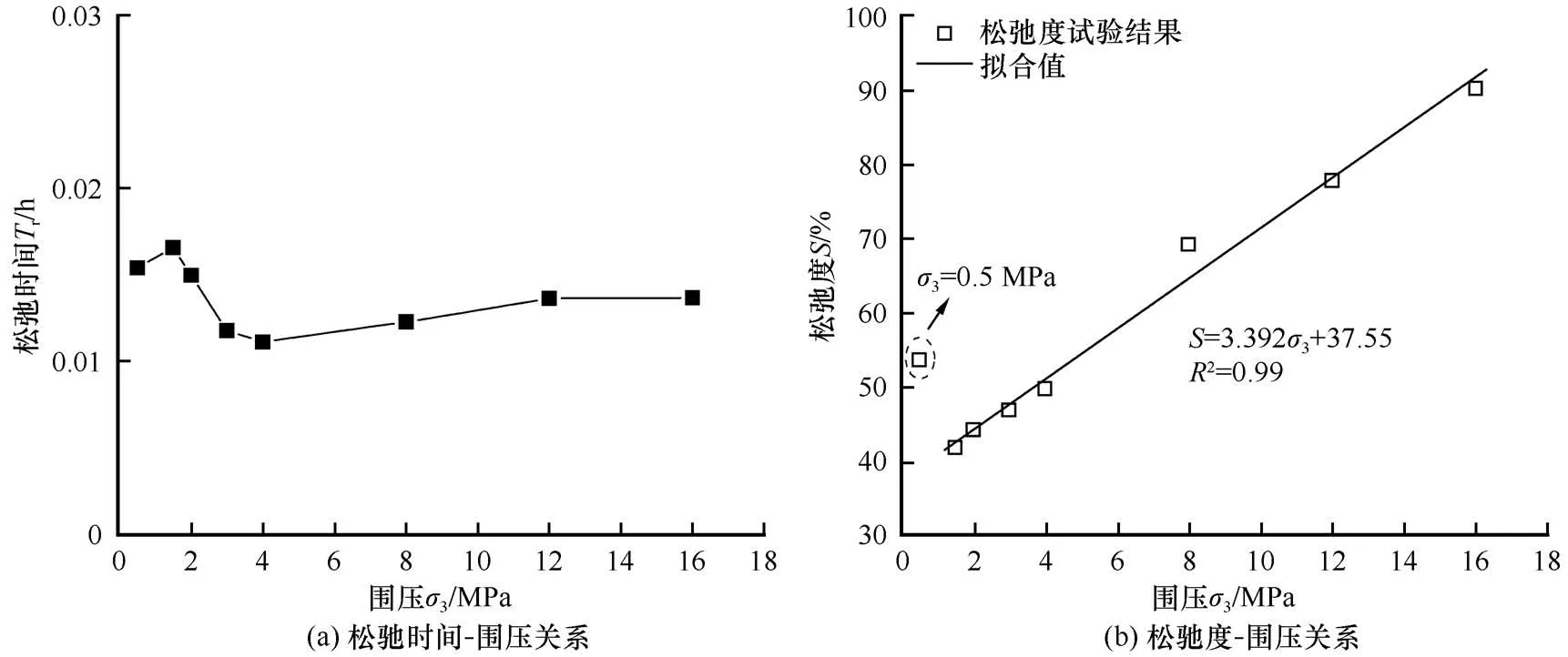
图5 松弛特性参数与围压的关系Fig. 5 Relationships between relaxation characteristic parameters and confining pressure:relaxation duration-confining pressure(a)and relaxation ratio-confining pressure(b)
图5(a)表明,松弛时间对围压的变化并不敏感。而由图5(b)可以发现,除0.5 MPa 围压外,其余试样的松弛度均随围压增大而线性增大,16 MPa围压下的松弛度达到了90.32%,而1.5 MPa下仅为41.94%。0.5MPa 围压下松弛度明显大于1.5 MPa的结果。初始松弛点的强度结果表明,围压为1.5 MPa 的强度明显高于0.5 MPa,这表明在这一较小围压范围内(σ3<1.5 MPa),围压的增大会压密土体而提高其抗松弛能力。在等预应变率、预应变量和等温条件下,冻土的抗松弛能力受围压影响明显,围压超过某一阈值时,围压的升高将大幅提高冻土应力松弛的强烈程度;而当围压较小时,围压的增大会提升冻土的抗松弛能力。
2.2 围压对冻土长期强度的影响
冻土应力松弛的试验结果可作为确定其长期强度的依据。研究人员基于大量试验结果提出了许多很好的经验模型用以描述冻土的应力松弛过程[7,10-13]并可据此确定冻土的长期强度。因此,本文仅选取其中能较好描述试验结果且简洁的长期强度方程进行分析。吴紫汪等[11]根据青藏公路风火山地区红色亚黏土的大量应力松弛试验结果发现,冻土破坏时间与应力的关系可用下式描述。

式中:σk为松弛初期对应于短时间tk的冻土强度;k为试验系数。由于松弛历时t=0 为该松弛模型的奇点,因此取松弛历时t=0.01 h 为tk,对应的偏应力为σk。使用该模型拟合的结果如图6 所示,对应的模型参数见表4,该模型能较好地描述冻结路基土在不同围压下的应力松弛过程。将表中的参数k与围压变化绘制于图7,发现在1.5~16 MPa 范围内,参数k随围压升高而线性增大,即应力与时间对数为线性关系且该直线斜率随围压升高而线性增大。而围压0.5 MPa 时的参数k则明显大于1.5 MPa 的结果。这在已有研究的基础上更新了对于冻土松弛特性影响因素的认识,即围压对冻土的松弛过程存在显著影响。参数k越大表明冻土抗松弛性能越差。基于冻土的两类关键强度机制(摩擦和冰的胶结作用)可以认为围压较小时(σ3<1.5 MPa),围压的增大会压密土体而增强摩擦作用。但随着围压继续增大(σ3>1.5 MPa),土体已被充分压密,而高围压使得土体内应力集中区的冰晶或冰包裹体出现破裂或融化,使得强度开始降低并表现出更强的流变特性[1,11]。为了准确考察复杂应力下冻土的强度衰减特性,基于数据仅对围压超过1.5 MPa 的试验结果进行分析。

图6 不同围压下应力松弛方程验证Fig. 6 Validation of stress relaxation equation under various confining pressures

表4 应力松弛方程拟合参数Table 4 Fitting parameters of stress relaxation equation
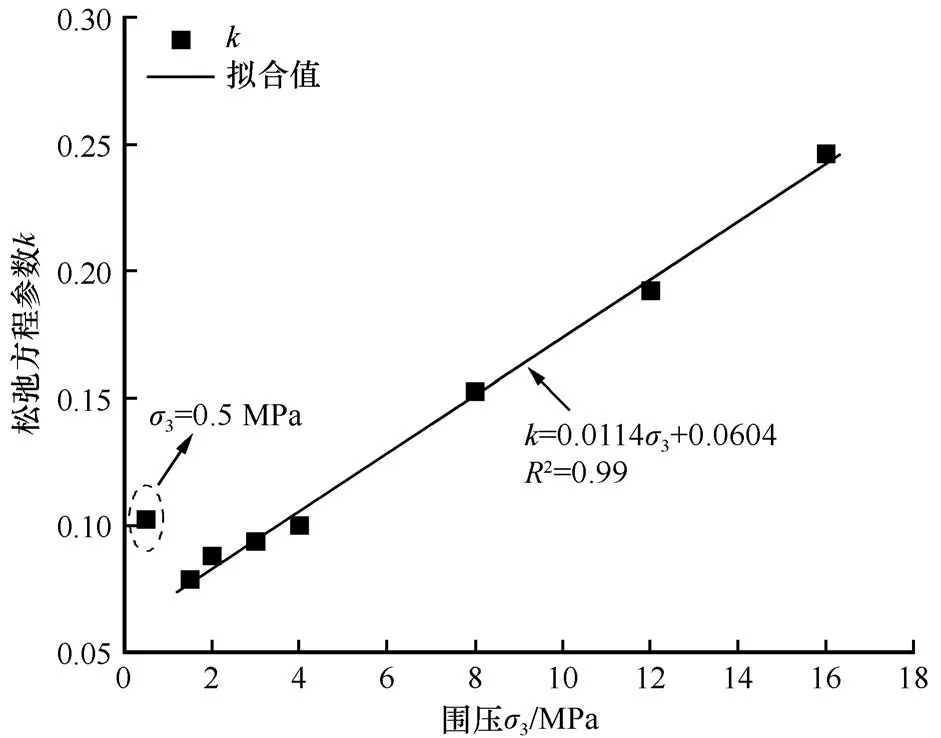
图7 松弛模型参数k与围压的关系Fig. 7 Relationship between parameter k in relaxation model and confining pressure
以上结果表明,在使用应力松弛试验确定冻土的长期强度时,围压的影响不可忽略,可将式(3)改写为
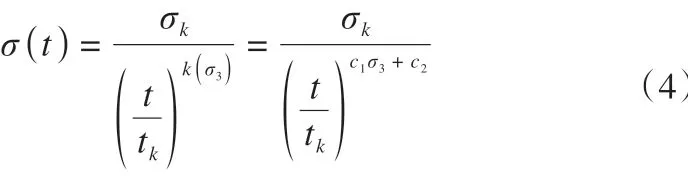
式中:c1和c2为拟合参数,本文中取0.0114 和0.0604。通过式(4)可求得任何时刻的强度,即为高围压下考虑围压影响的冻土长期强度方程。
2.3 复杂应力状态下冻土的强度衰减特征
大量研究表明,土的强度主要取决于两种机制——黏聚力和摩擦抗力。冻土中冰的胶结作用以及冰晶的存在加强了这两种作用,从而使得土体冻结状态下的强度远高于融化状态[1,31]。因此,流变过程中这两种作用的演化规律可在一定程度上反映冻土强度衰减过程的内在变化,并为分析复杂应力状态下的冻土强度衰减特征提供参考。这两种作用在Mohr-Coulomb 理论中对应两个强度参数,即黏聚力(c)和内摩擦角(φ)。基于本文的试验结果,可通过松弛过程中不同围压下试样任一时刻的应力状态绘制摩尔圆及其包络线,以此求得任一时刻冻土的黏聚力和内摩擦角。通常选取较小围压下的线性段来获取冻土的等效黏聚力(c′)和等效内摩擦角(φ′)[32-33]。如图4 所示,从松弛初始点t0开始,本文提取了12 个时刻下试样的应力状态,并绘制摩尔圆及其包络线(图8)。
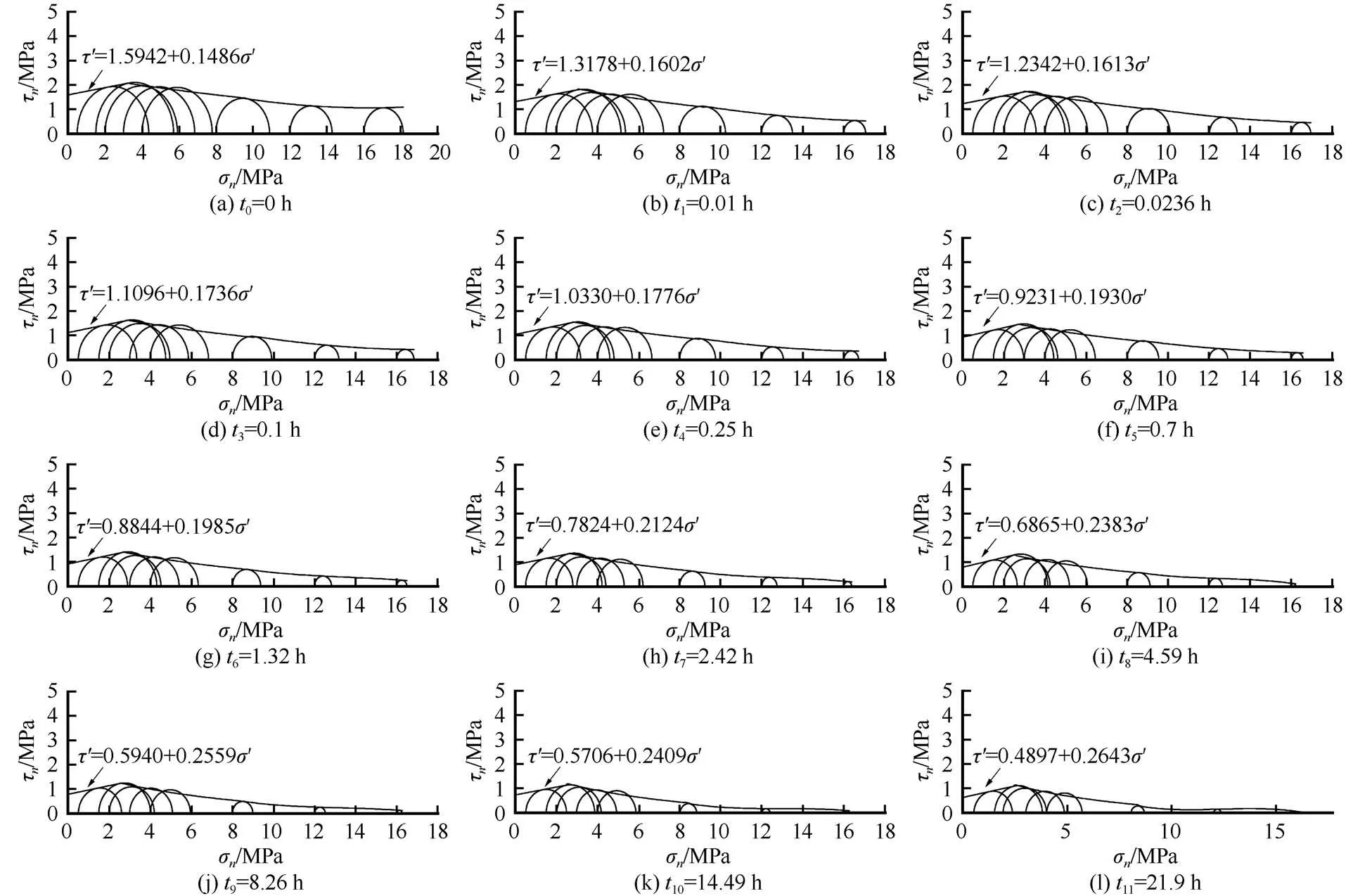
图8 不同松弛历时下的莫尔应力包络线Fig. 8 The Mohr strength envelopes at various relaxation durations
12 个松弛历时时刻对应的等效黏聚力和等效内摩擦角列于表5。随着时间的发展,c′逐渐减小,φ′则逐渐增大,即冻土的黏聚力作用减弱,而摩擦作用增强。冻土的黏聚力与内摩擦角这两个关键强度参数均与时间直接相关,具有率相关特性。在评价冻土强度特性及相关参数时,时间的影响不可忽略,该影响在常规三轴试验中常体现为加载速率(应力率或应变率)。冻土的黏聚力主要取决于冻土中冰的胶结作用,该胶结作用既大幅提高了冻土瞬时强度,也使得冻土成为强流变材料,流变过程会弱化该联结作用,从而表现为冻土的黏聚力随时间发展而降低,这是冻土强度衰减的重要组成部分。另一方面,获取冻土等效黏聚力和内摩擦角在本文中取自围压为0.5 MPa 和1.5 MPa 的试验结果,在此围压范围内,围压的增大会压密土体,提高冻土强度,围压增大所产生的摩擦强化作用为主导。强度衰减过程中,0.5 MPa 围压下的衰减程度和速度均大于1.5 MPa 围压的情况,这由图3(b)中应力松弛率的结果可以印证。这使得包络线在下降过程中会发生逆时针转动,表现为内摩擦角逐渐增大。
为定量分析等效黏聚力和等效内摩擦角随松弛历时的变化规律,将各松弛历时下的c′和φ′绘制于半对数图内,如图9所示。在半对数坐标系中,等效黏聚力和等效内摩擦角随时间发展呈线性变化,可分别表示为
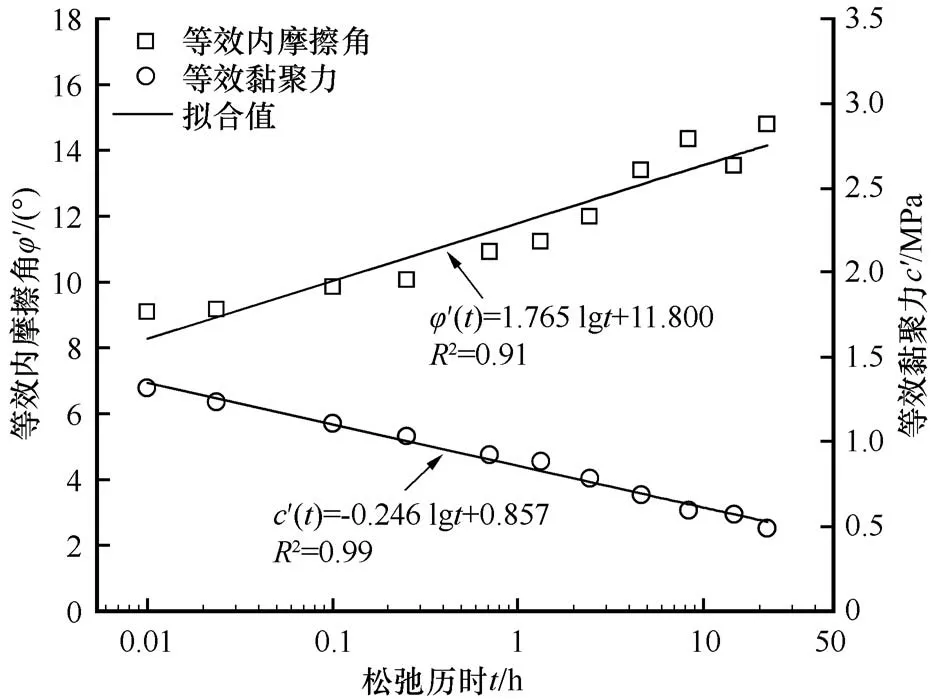
图9 等效黏聚力与内摩擦角随时间的变化Fig. 9 Variations of equivalent cohesion and internal friction angle with time
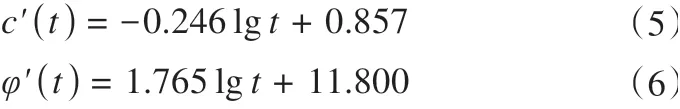
式中:lg 为对数函数,以10 为底。本文所求得的等效黏聚力的量值及其随松弛历时的发展规律与维亚洛夫[7]通过球形压板法所测得的多类土质的长期黏聚力强度试验结果极为接近。可以猜想,冻土三轴应力松弛试验所确定的等效c′与长期黏聚力强度之间可能存在某种相互关系,但此关系需通过大量的相关试验结果来建立。冻土的长期黏聚力与内摩擦角是多种冻土地基承载力计算方法中的重要参数[1,7],若此关系存在,则可更加准确、便捷地对冻土地基承载力进行评价。
以上对冻土两种强度机制在松弛过程中的衰减规律的研究加深了对冻土强度衰减特性的认知,接下来在此基础上对冻土强度面随时间发展的演化过程进行深入的分析和讨论。本试验中,预应变量为15%,松弛初始点即为该试样的破坏强度点。将各围压下的强度点绘制于p-q空间内可得到冻结兰州路基土的强度包络面(图10)。马巍等[34]基于蠕变试验将冻土的抛物线屈服准则推广为长期强度准则,且当强度包络线的位置随时间和温度变化时,包络线保持几何一致。该抛物线型长期强度准则可很好地描述前两个围压阶段冻土强度面随时间发展的演化规律。但由图10可知,本试验中人工冻结路基土的初始强度面随围压升高存在明显的三阶段特征,即快速增大,快速降低和缓慢降低。经过多年来大量学者的研究,这一现象可归结于围压对冻土的两种影响机制在不同工况下耦合的结果:①围压较小时,围压压密土体,并增大了土体内固体颗粒的接触正应力,使得固体颗粒间的摩擦、咬合作用增强,从而增大了冻土的强度;②高围压时,冻土内的部分冰晶逐渐破碎、融化,对于粗颗粒土,甚至出现土颗粒破碎,土体结构受到损伤,降低了冻土的强度[19,21,24]。高低围压的界定相对于不同类型的冻土是不同的。围压对冻土强度的影响本质上是通过压力改变冻土内在结构性联结作用的具象表现。冻土的流变特性受制于其内冰的结构联结作用,因而冻土的结构性差异也可能导致其流变特性存在差异。本文试验结果已证实,在相等的大预应变量、预应变率和温度下,高围压下围压的升高(本文中为σ3>1.5 MPa)会直接减弱冻土的抗松弛能力,围压越大,松弛度越高,16 MPa下残余强度小于初始强度的10%。因此,研究高围压下冻土强度衰减特征需要使用能够完整描述冻土强度包络面三阶段特性的强度准则。Shen 等[35]基于大量试验结果,建立了考虑应力路径影响的冻土非线性强度准则,该准则可完整描述冻土强度随围压升高的三阶段发展特征,其数学形式为
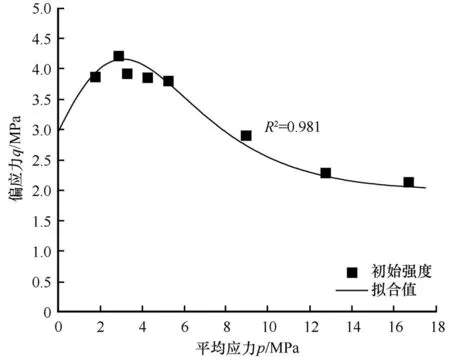
图10 初始强度面Fig. 10 Initial strength surface
式中:φ′为等效内摩擦角;qm和pm分别为试验强度面峰值强度及对应的平均应力;a1和a2为试验参数;qcr和pcr为假定的第三阶段稳定强度和对应的平均应力,且当平均应力p趋于无穷大时,该强度准则变为q=qcr,即von Mises 强度准则。使用该强度准则拟合初始强度面的结果如图10所示,该准则可较好地描述冻结路基土强度随围压增大的变化特征。本文以此强度准则来研究人工冻结路基土在复杂应力状态下的强度衰减特征,并基于此将该强度准则推广为长期强度准则。
基于试验结果获取的松弛历时t0~t11共计12 个时刻不同围压下各松弛曲线所对应的应力状态,整理得到各时刻下的试验强度点,汇总于图11。可以发现,初始时刻与松弛历时t1=0.01 h 强度面的距离随着围压的增大而明显变大。各围压下t1与t11时刻强度差值随着围压增大逐渐减小。具象化来说,强度面随时间的发展除高度下降外,还发生了一定程度的顺时针转动,且强度面第三阶段先变陡后变缓。强度面第三阶段的变化反映了冻结路基土高围压下的强度衰减程度更高,且松弛初期更加剧烈。这表明冻土强度包络面的第三阶段在随时间的发展过程中无法保证几何一致性。高围压下冻结路基土的强度包络面随时间发展在p-q空间内的变化过程是复杂的空间和形状的变化。处理这类问题最直接有效的方法是对任意时刻强度包络面的数学描述进行参数分析。使用式(7)作为所有松弛历时下强度面的数学模型,对其中的参数a1、a2、qcr和pcr进行敏感性判断发现,a2和pcr可为常数。由式(7)的结构和参数定义可知,a2的作用为调节试验强度面与理论强度面峰值位置的对应关系;pcr代表试样进入稳定第三阶段的假定平均应力值,理论上是冻土内部结构对围压的临界响应值,为材料的固有特性,不会随松弛过程发生改变,本试验中pcr的值与多应力路径下(温度-6 ℃,ε̇a=7.62×10-5s-1)的结果[35]相同也印证了这一点。因此,需要进行拟合的参数仅有a1和qcr。对12 个松弛历时时刻的强度面进行最佳拟合,拟合曲线结果如图11 所示,拟合参数见表6。为使图像清晰,仅展示了部分拟合曲线,该模型可较合理地描述冻结路基土在任一时刻的试验强度面。
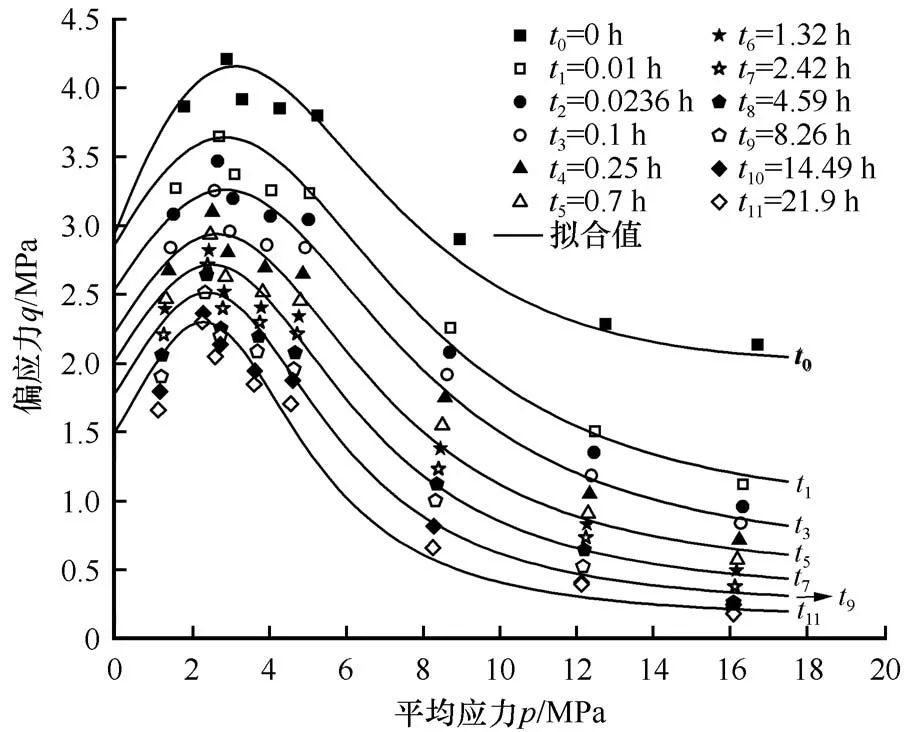
图11 不同松弛历时下p-q平面内的强度包络面Fig. 11 Strength envelope surfaces in p-q stress space at various relaxation durations
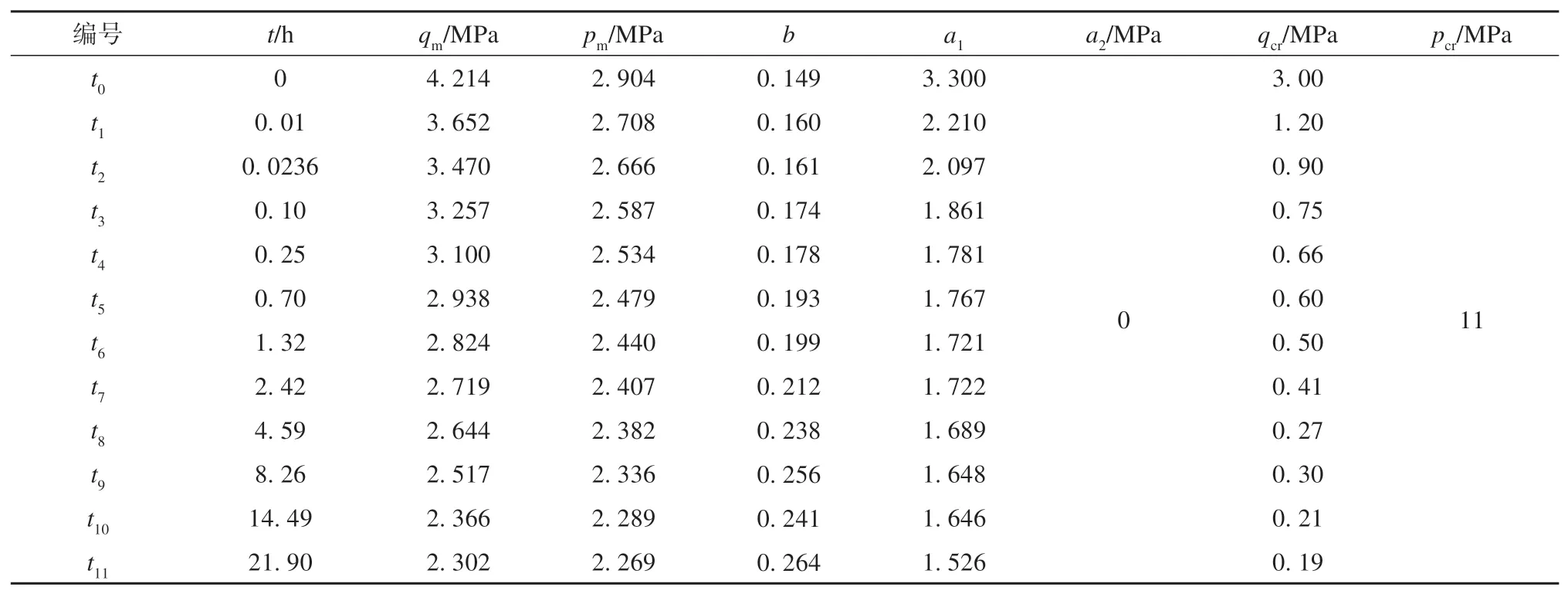
表6 不同松弛历时下的强度面拟合参数Table 6 Fitting parameters of strength surface at various relaxation durations
该强度准则中参数b和qm通过计算直接获取。任一松弛历时t下参数b可根据本文研究成果计算,即式(6)和式(8);qm为峰值强度,服从长期强度方程,在本文中可按下式计算。

将qcr与松弛历时的关系绘制于图12(a)。分析后发现,qcr同样遵从长期强度方程。

参数qcr随松弛历时发展的规律表明qcr可能为某一围压下试样的强度值。而qcr与qm随时间发展的变化代表了冻土强度在两种围压状态下的衰减过程,结合前述对等效黏聚力的分析,实际上这其中包含了冻土黏聚力的降低。
对于常规三轴压缩试验,加载全过程围压σ3为常数,且具有轴对称条件,平均应力p与偏应力q定义为p=(σ1+2σ3)/3,q=σ1-σ3。则可得
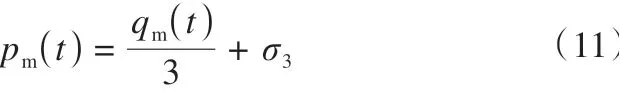
结合式(9)、式(11),则可计算任意时刻下pm的值。参数a1与松弛历时在半对数坐标中的关系如图12(b)所示,参数a1与松弛历时呈对数关系。
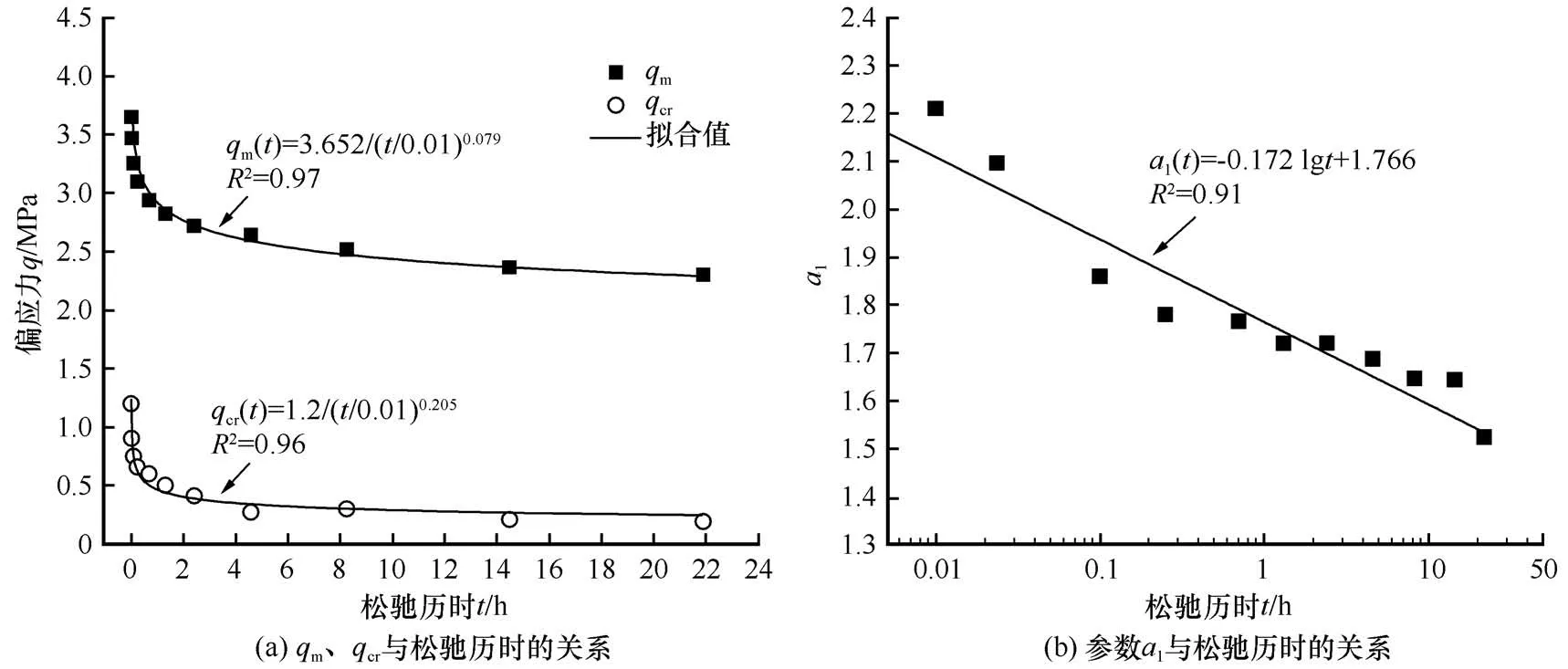
图12 强度包络面关键参数与松弛历时的关系Fig. 12 Relationships between key fitting parameters of strength envelope surface and relaxation duration:qm,qcr-relaxation duration(a)and parameter a1-relaxation duration(b)
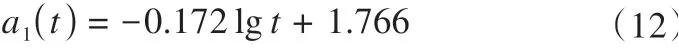
式中:lg为对数函数,底为10。
根据以上分析,该强度准则在p-q空间内可改写为
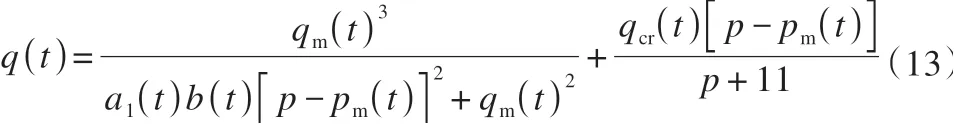
由式(6)、(8)~(13)就可以确定任意时刻下冻土的强度包络面,即通过应力松弛试验确定了考虑高围压影响的冻土长期强度准则。
3 结论
本文通过强度点处的应力松弛试验研究了复杂应力状态下冻结路基土的应力松弛特性及其强度衰减特性,得到以下结论:
(1)冻土的应力松弛过程受围压影响明显,围压超过1.5 MPa 时,随围压增大,松弛度线性增大。围压为16 MPa 下的松弛度超过了90.32%,而1.5 MPa下仅为41.94%。
(2)围压会影响冻土强度衰减速率,从而影响冻土的长期强度。冻土强度在半对数坐标中随时间发展而线性降低,当围压大于1.5 MPa时,直线斜率随围压升高而线性增大,即冻土强度衰减速率随围压增大而升高。
(3)冻土的强度衰减过程中,黏聚力逐渐下降,内摩擦角逐渐增大,且均与松弛历时的对数呈线性关系。通过三轴应力松弛试验获得的等效黏聚力衰减规律及量值与球形压板法的直接测量结果接近,这为获得冻土的长期强度及其黏聚力参数的提供了新的研究思路和试验方法。
(4)随着时间增长,具有三阶段特征的冻土强度包络面无法保证严格的几何一致性。强度包络面随时间的发展除水平下降外,还发生了一定程度的顺时针转动,且强度面第三阶段先变陡后变缓。基于对冻土试验强度包络面特征的分析以及强度参数在强度衰减过程中的演化规律,本文建立了考虑应力松弛效应的冻土率相关强度理论。
