基于变论域模糊控制的高旋弹姿态控制算法
2022-06-14申强万初朋高潇王晗瑜
申强,万初朋,高潇,王晗瑜
(北京理工大学 机电学院,北京 100081)
二维弹道修正技术已成为近年来对中大口径加榴炮高旋弹药进行精确化改造的一种主要途径[1]. 其中,采用双旋体鸭式舵的设计方案只需将头部引信部分替换为精确修正组件,弹丸主体部分仍保持高速旋转即可实现二维弹道修正的目的,相较于加装尾翼、整体减旋的制导炮弹而言,对射程和稳定性影响较小,具有成本低廉、修正力连续可控、适应性强、修正效率高、易于安装和小型化等优点[2]. 但是,由于高旋弹体自身强耦合、非线性、干扰不确定的特性,目前对采用双旋体鸭式舵进行二维弹道修正的研究主要集中在弹道模型、修正控制算法、修正能力、弹道特性等方面,且大部分仅对弹道进行闭环控制,对姿态控制的研究成果并不多见[3],而对弹体姿态进行控制能加快弹道修正响应速度、提高修正能力,改善弹体响应特性. 因此,针对双旋体鸭式舵高旋弹丸在飞行过程中参数时变、扰动不确定以及强耦合的问题,设计出具有较好的控制精度和自适应性的姿态控制器具有重要意义.
采用反馈控制的方法调节弹体姿态能一定程度上抑制系统内部特性的变化和外界干扰,且相较于其他复杂的控制系统,具有结构简单、易于工程实现的优点,但当系统的参数实时变化或者外界干扰很大时,系统超调较大,响应延迟时间较长,控制效果变差. 变论域模糊控制是在保持模糊控制规则不变的前提下,通过使论域随着误差大小而伸缩从而增大规则库、提高精度的一种自适应模糊控制器,它既继承了模糊控制对于复杂不确定系统的高适应性,又提高了精度[4−7]. 为此,提出了一种将反馈控制与变论域模糊控制结合的姿态控制方法. 通过变论域模糊控制器对反馈控制系统参数进行自适应整定,使其兼顾变论域模糊控制灵活性好、鲁棒性强的特点和反馈控制结构简单易于实现的优点,实现在复杂条件下对弹体姿态的快速稳定跟踪控制. 设计了弹体姿态控制器,仿真验证了其控制性能.
1 双旋体鸭式舵弹道修正控制原理
双旋体鸭式舵弹道修正控制原理如图1 所示. 将弹丸头部引信替换为精确修正组件,并使其相对弹轴保持静止不转,4 个鸭舵舵偏角 δc均可调,通过调整其相对弹轴坐标系oη 轴 的转角 γc和 舵偏角 δc,在来流的作用下,可产生不同大小及方向的控制力矩对弹丸的俯仰和偏航姿态进行控制,从而产生修正控制力对弹道进行射程和横偏方向的修正.

图1 双旋体可动鸭舵二维弹道修正引信Fig. 1 Trajectory correction fuze ofdual-spinning projectile equipped with movable canards
2 双旋体鸭式舵姿态控制模型
2.1 弹丸角运动模型
在弹丸飞行过程中,可将弹丸看做一个刚体,其运动可分为两部分:一是质心运动;二是围绕质心的转动. 由于弹体高速旋转,且采取双旋体结构,因而不对弹丸的滚转姿态进行控制. 由动量矩定理可推导描述弹丸围绕质心的俯仰、偏航姿态的变化方程,在弹轴坐标系中可表示如下[8].
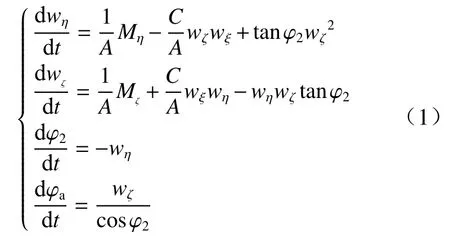

2.2 姿态控制模型
假设弹丸的质量分布、气动分布对称,一小段时间内可将速度和转速看作固定值,且不考虑风的影响. 采用(小扰动、线性化)系数冻结法,可以得到弹体姿态的扰动运动方程组


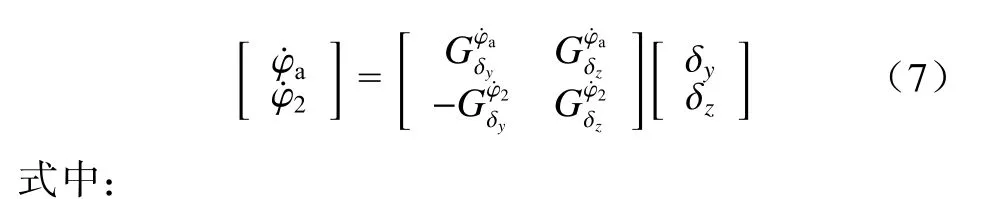
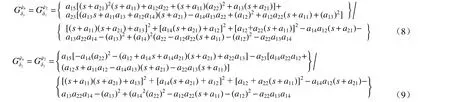

3 基于变论域模糊控制的参数自适应姿态控制器
首先通过前置反馈补偿的方法对上文建立的姿态控制模型进行了解耦,接着设计了反馈控制系统,并通过变论域模糊控制器敏感姿态角误差和姿态角误差变化率实时调整反馈控制器参数,达到了反馈控制系统参数自适应调节的目的.
3.1 前置反馈补偿解耦模型


图2 前置反馈补偿解耦结构图Fig. 2 Decoupling structure of pre-feedback compensation
以某155 mm 双旋体二维弹道修正弹为对象,在炮兵标准气象,初速930 m/s,射角51°,弹体初始转速300 r/s,引信初始转速为0 的初始发射条件下,选取弹道顶点进行分析,得到解耦前后弹体姿态响应情况如图3,图4 所示.
由图3 可见,弹体俯仰和偏航方向存在耦合效应. 其中,正(负)的俯仰输入引起正(负)的偏航耦合,正(负)的偏航输入引起负(正)的俯仰耦合,这一方面表明高旋弹体在无控状态下,姿态角运动是滚转稳定的,高旋弹弹体的姿态稳定是依靠高速旋转实现的;另一方面也表明耦合交连作用不仅会引起不必要的耦合响应输出,也会削弱控制效果. 由图4 可见,解耦后,系统的俯仰−偏航耦合响应基本消失,可 对俯仰个偏航通道进行单独设计,以改善其动态性能.

图3 解耦前δ y、δ z单位阶跃输入时姿态角响应Fig. 3 Attitude angle response of δy and δz unit step input before decoupling

图4 解耦后δ y、δ z单位阶跃输入时姿态角响应Fig. 4 Attitude angle response of δy and δz unit step input after decoupling
3.2 姿态反馈控制模型
由于弹体结构的对称性,俯仰、偏航通道的设计方法完全相同,这里仅对俯仰通道进行设计. 图5 为弹体姿态反馈控制的典型结构,其输入指令通常是姿态角指令 φac, 控制过程中需要反馈弹体的姿态角φa和 姿态角 速度 φ˙a,其 中, φ˙a可由角速度陀螺 测得,而φa可以由姿态陀螺或角速度陀螺信号经积分得到[11].
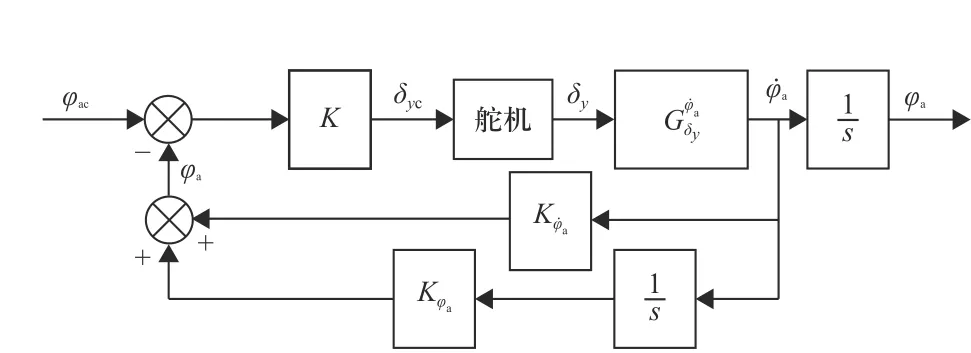
图5 姿态反馈控制的典型结构Fig. 5 Typical structure of attitude feedback control


3.3 基于变论域模糊控制的参数自适应控制器
由式(5)可知,影响弹体动态响应特性的参数诸如空气密度、弹体飞行速度、弹体转速、马格努斯力矩系数导数、舵升力系数导数等在弹体飞行过程中取值是不断改变的,这对姿态反馈控制系统的适应性和鲁棒性提出了更高的要求. 因此,引入变论域模糊控制器对反馈控制系统的参数进行在线自整定.
3.3.1 变论域模糊控制

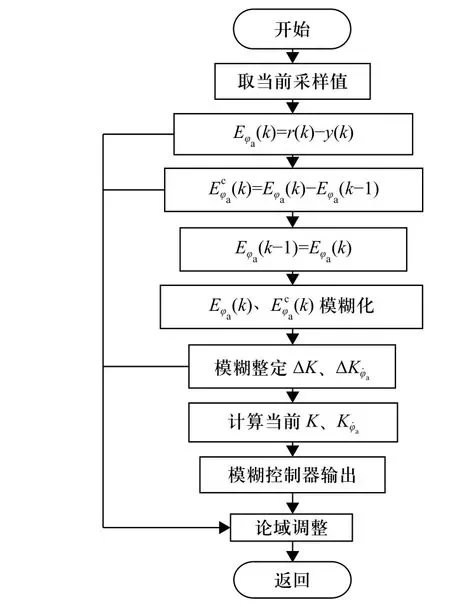
图6 变论域模糊控制参数自整定流程图Fig. 6 Parameter self-tuning process of variable universe fuzzy control
3.3.2 输入输出模糊集及变论域伸缩因子
一般地,将姿态角误差Eφa、姿态角误差变化率以 及 输出调整量 ∆K、 ∆Kφ˙a均分 为7 个等级,依次为NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大),Eφa、的论域范围均为[−3,3],∆K、∆Kφ˙a的论域范围分别为[−0.3,0.3]、[−0.06,0.06]. 输入输出的隶属度函数分布,NB 采用Z型隶属度函数,PB 采用S型隶属度函数[12].
常规模糊控制的论域范围通常是不变的,故具有一定的局限性:当论域范围较小未包含输入输出的调节范围时,会导致系统超调,控制效果变差;当论域范围较大时,则会使模糊规则的调节作用下降,导致精度下降[13]. 因此需要引入变论域的思想,使基本论域范围在输入输出变量增大时使相应的论域扩展,减小时使相应的论域收缩

变论域模糊控制在每一步计算中都要对变量所对应的所有隶属度函数峰点或模糊单值元素论域进行伸缩变换,采取指数型或积分型伸缩因子时,可能会导致运算量超出处理器的处理能力[14],因此,采用相对简化的比例型伸缩因子进行变论域操作. 如下,推理前件伸缩因子采用式(13),推理后件伸缩因子采用式(14)

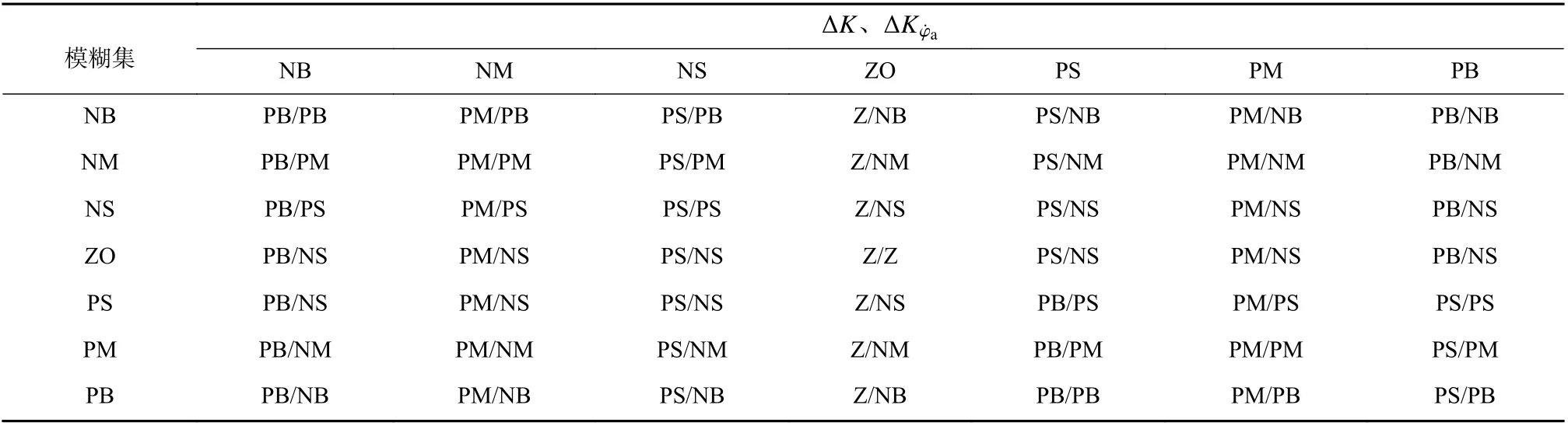
表1 模糊控制规则表Tab. 1 Table of fuzzy control rule
推理机及解模糊器不作为本文研究内容,采用Zedal 推理机进行模糊推理,重心解模糊器将所得到的模糊推理结果转化为精确值.
4 仿真验证
在3.1 节中的初始发射条件下,K、Kφ˙a分别取为601、0.19,取弹道下降段为修正段,时间0 点为弹道顶点,每隔10 s 进行一次修正. 对加入变论域模糊控制器前后弹体姿态控制系统响应情况进行分析,结果如图7 所示.

图7 弹体姿态角响应Fig. 7 Attitude angle response of projectile
由图7 可知,由于弹丸姿态控制模型在弹道上随着各飞行参数不断变化,采用固定参数的姿态反馈控制系统在弹道不同阶段的控制性能波动较大,适应性较差,其中由于弹道顶点附近弹丸稳定性较强、可控性较差,因此弹丸姿态角响应慢于弹道末端,超调量也较大,调节时间较长. 统计弹体姿态响应性能结果见表2.

表2 弹体姿态响应性能对比Tab. 2 Comparison of attitude response performance
由表2 中结果可知,加入变论域模糊控制器后,有效地改善了弹道顶点附近姿态闭环反馈控制系统控制性能,前3 次修正超调量分别由31.5%、23.1%、10.4%减 小到 14.5%、8.2%、8.5%,调节时间分别由3.25、2.63、1.09 s缩 短到 1.41、1.06、0.75 s,对后2 次控制性能较好的则几乎没有影响. 说明所设计的变论域模糊控制器能有效改善姿态闭环反馈控制系统的动态响应特性,减小弹体参数时变对控制器性能的影响,提高其适应性.
5 结 论
本文利用变论域模糊控制器设计了高旋弹姿态参数自适应反馈控制算法. 通过姿态角误差Eφa、姿态角误差变化率Eφca 实时调整反馈控制系统前向主增益K、阻尼增益Kφ˙a的取值,有效加快了系统的响应速度,提高了控制精度和适应性. Matlab 仿真表明:所设计的姿态控制器具有较好的参数自适应性,能够实现弹体姿态的快速、精确控制,有利于提高二维弹道修正弹的修正效率和精度. 在未来的工作中,将进一步研究优化变论域控制器设计参数,以提高其对姿态反馈控制系统性能的改善效果.
