基于脉冲增益的开关电源磁芯复位仿真

袁 帆，宋 岚

(陕西理工大学电气工程学院，陕西 汉中 723001)

1 引言

脉冲功率能都提升开关的功率及长寿命，在磁开关技术中占据重要地位。磁开关的本质是通过铁磁材料导磁率的变化特性实现电路工作状态转换，从而起到能量转移等作用。磁开关技术的进步同时也改善脉冲功率使用寿命短、重复率低等缺陷。磁开关在电路中主要作用体现在：脉冲压缩与脉冲波形的锐化与修整。磁芯属于磁开关的关键部件，它的复位情况会影响磁开关性能和脉冲增益效果。因此对其复位要求格外严格。为改善传统磁芯复位方式准确度差、效率低的问题，相关学者提出下述复位方法。

文献[1]研究一种容量较小双谐振有源箝位反激升压变换器拓扑。初级利用有源箝拉电路，减少开关管应力，使控制方式更为简便；次级则采用双谐振电路，提高功率密度与变换器整体效率；分析变换器的工作状态，根据其稳定性对电路参数进行设置，从而实现开关电源磁芯复位。文献[2]通过分析有源复位电路的工作原理，在LC谐振原理基础上推导出全部阶段的复位电流、电压值，并在Simulink模块中搭建电路仿真模型，通过实验对比说明复位电路设计的可行性。

上述两种方法均实现了开关磁芯复位，但是没有考虑脉冲在增益介质中传播特性，会在一定程度上影响复位精准程度。因此提出基于脉冲增益的开关电源磁芯复位仿真。首先建立一个含损耗情况的脉冲放大器模型，获取光在介质中传播时符合的频域波动方程与放大器增益通量曲线；其次分析磁芯复位工作基本原理，对磁芯动态参数进行测量，通过公式推导出复位的电流取值；最后仿真结果表明，所提方法提高开关电源磁芯复位的准确率，减少复位时间，不会出现消电离与电极烧蚀情况，可以保障系统正常运行。

2 脉冲传输特性与增益通量曲线研究

2.1 脉冲放大器模型及脉冲在增益介质中的传播方程

建立一个如下所示含损耗的脉冲放大器增益通量耦合模型

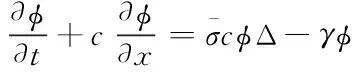
(1)

光脉冲在不同介质中传播时符合的频域波动表达式为

(2)

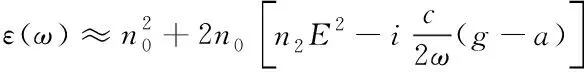
(3)

式中，n0是背景折射率，n2属于非线性折射率系数，n2|E|2表示由于非线性现象导致的介质折射率变换情况，g代表增益系数，体现出介质在不同光场中增益不同，a属于介质损耗系数，描述介质对不同光场的损耗程度。若在介质中按照z方向传播的是准单色线偏振光，此时光场能够表示为

E(r，t)=F(x，y)A(z，t)exp(ik0z-iω0t)

(4)

(5)

式中，k(ω)表示ω频率分量波数，对其在脉冲频率为ω0处进行泰勒级数展开[5]可得到

(6)

即使介质增益峰值频率ωg与脉冲中心频率ω0不相同，但是仍然能够将其在ω0处进行泰勒级数展开，表达式为

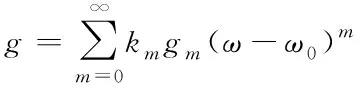
(7)

式中，当m=0时，k0与g0分别表示ω0频率分量在介质中存在的波数与增益系数；当m=1时，k1、g1则代表ω0频率分量群速度的倒数与增益斜率；当m=2时，k2与g2分别表示群速度色散情况与增益色散；当m≥3时，km、gm描述高阶与高阶增益色散，将方程(7)与(6)带入到(5)中，并对其进行傅里叶变换[6]，此时可以得到

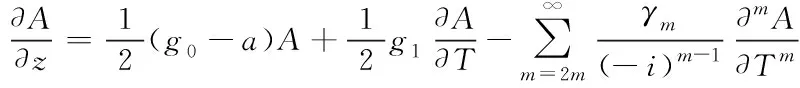
(8)

上述公式表明脉冲在增益介质中传播时，脉冲传输性质会随非线性效应、色散情况以及增益的变化发生改变。

2.2 放大器增益通量曲线

脉冲在增益介质中传输时需要符合下述放大运输表达式

(9)

将输入脉冲和输出脉冲两者关系进行对比，就可以获得脉冲信号的放大倍率G1(η，τ)

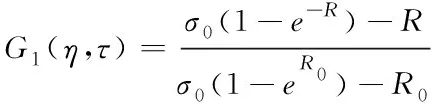
(10)

在对损耗忽略不计时，上述表达式利用初等函数表示为

(11)

上述表达式是通过归一化参量[7]后获得的，假设I=Ahvcφ代表激光脉冲功率，A表示通光面积，L描述介质长度，则可得到下述表达式

(12)

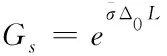
根据上述描述获得增益通量曲线，不但对放大器有进一步认识，而且为实现功率平衡提供有效工具[8]。

3 基于脉冲增益的开关电源磁芯复位方法

3.1 磁芯工作原理分析

在结束励磁后，励磁电流变为零，与磁芯通磁量密度B相对的值为剩磁。针对低剩磁的磁芯，通常情况下伏秒值对应的剩磁Br均趋近零。通磁量密度从Bs下降到Br属于一个自发过程[9]。所以ΔB=Bs-Br，与其相对的伏秒值是能够重复使用的，在Br接近于零时，此部分伏秒值是总伏秒值的二分之一。

因此，假设多脉冲感应腔利用低剩磁芯，则在不存在其它复位状况下，也可以重复使用磁芯一半的伏秒值，并且不会受到脉冲总数与幅度的制约。但是，低剩磁芯在脉冲感应腔应用时，需要符合下述条件：

1)磁芯在不同环境下必须具备充足的磁导率，结合单脉冲直线感应器设计原理，平均磁导率不能低于300，否则感应腔不能保持脉冲的平顶；

2)磁芯可以产生足够大的伏秒值：针对单独脉冲来说，低剩磁芯ΔB=Bs-Br，若Br=0.1B，则ΔB=0.9B，而针对高Br磁芯来说ΔB=Bs+Br≈2Bs。

3)在经过励磁后，磁芯磁通量密度自动恢复的时间Δτ需要很短，高压多脉冲间隔必须小于1μs，确保磁芯的自动复位时间低于脉冲间隔[10]。

3.2 磁芯动态参数测量

电感的伏秒积平衡方程表示为

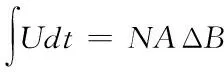
(13)

式中，N代表绕组匝数，A表示磁芯横截面积。因此能够获得

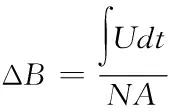
(14)

结合安培环路定理可以得出

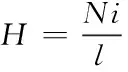
(15)

式中，i代表回路电流，l表示磁芯平均磁路。

根据上述可知，利用示波器测量且记载开关MS两端的电压值，采用计算机对其进行积分，即可计算得出磁感应强度B。通过分流器测试回路电流，从而获得磁场强度H。

针对环形磁芯来说，对应参数计算公式为

(16)

A=(r0-r1)h

(17)

式中，r0和r1分别表示磁环的外半径与内半径，h是磁环高度值。

3.3 开关电源磁芯复位

除此之外，根据磁芯剩磁的原理可以得出，自动恢复到剩磁的时间与线圈中电流变为零的时间是相同的。磁导率越高，线圈阻止电流改变的性能越好，因此电流变为零所需的时间越长，自动恢复的时间也随之增加。所以为使磁芯恢复时间较短，必须确保磁导率不能太大。

综上所示，为满足磁芯恢复时间较短的要求，需要符合两个条件：一是负载阻抗要尽量达到最大；二是磁导率应该在其下限值300附近。

如果磁芯在脉冲励磁过程中时，磁芯的线圈属于功率系统的负载，在有电流通过线圈时，磁芯会具有一部分能量。在结束励磁时，因为电感的存在，磁芯线圈会影响电流的速度，这时开关已经将功率源切断，能使电流继续存在的只有磁芯自身能量的释放[11]，因此，线圈由负载转化为电流源。针对电流源而言，负载阻抗越高，两边的电势差别越大，所以，主脉冲在完成励磁后，电流线圈负载越大，磁芯自动复位形成的反极性电压起伏越高，自动恢复所需时间也就越短。

本文对磁芯进行复位的方式为：磁开关之外添加复位绕组，将其和主绕组进行隔离，复位绕组通过固定大小的电流，该电流就是复位电流。复位电流的取值可以通过下述表达式计算。

根据麦克斯韦-安培方程可得

(18)

Bl=μ0NrI

(19)

(20)

将上述表达式联合可以得到

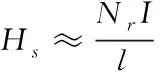
(21)

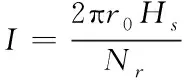
(22)

式中，μ0表示在真空中的磁导率，J代表导线的电流密度，A属于导线横截面积，I描述电流大小，H表示磁声场强度，Hs是反向饱和区域的磁场强度情况，单位是A/m，Nr表示复位绕组匝数，r0是平均半径长度，单位是m，l代表磁路长度，针对环形磁芯来说，该长度值可以近似等于2πr0。

为保证磁芯可以进入到深度反向饱和区域，复位电流I0要符合下述条件

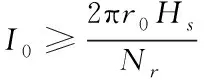
(23)

因为主绕组和复位绕组耦合的磁芯相同，根据匝数变换情况得出复位绕组两端的电压值，计算公式为

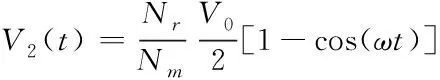
(24)

耦合在复位绕组两侧的电压，在复位电路中会形成感应电流，计算此电流的公式为

(25)

式中，Nm表示主绕组的匝数。

则复位回路的电流表示为

i(t)=Ipeakcosωt

(26)

由此可以计算Lr两侧电压值，且对电压进行求伏秒积分

〈vrtr〉=LrIpeak[cos(ωtr)]

(27)

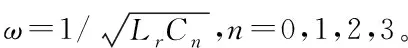
因此计算得出

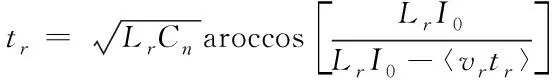
(28)

因为在复位电路中会有许多寄生参量[12]的存在，上述表达式只能对复位时间进行近似表示，通过此公式即可实现电源开关磁芯的准确快速复位。

4 仿真数据分析与研究

为验证上述研究的基于脉冲增益的开关电源磁芯复位方法的有效性，搭建测试磁芯复位仿真系统，验证所提方法性能。实验在MATLAB仿真软件中进行，在该软件中搭建测试磁芯复位仿真模型，其中，L1与L2均为电感，复位绕组将磁开关中耦合出的高压用来确保复位电源的稳定性；C1表示电容，R2为电阻，D1属于二极管，这三项组合为衰减吸收回路，可以吸收残余能量，保证电流的稳定。磁芯复位仿真模型如图1所示。

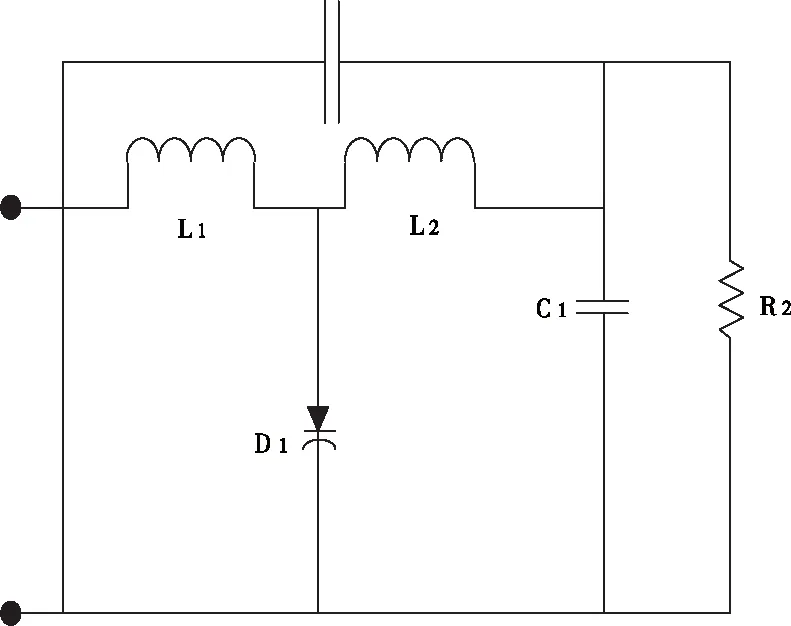
图1 磁芯复位仿真模型

为证明所提方法的优越性，采用文献[1]方法、文献[2]方法做为实验对比方法，将复位精准度与复位所需时间作为对比标准，得到复位精准度对比结果如图2所示。

图2 不同方法复位精准度对比图

根据2可知，采用文献[1]方法进行7次开关电源磁芯实验，得到的复位精准度平均值为55%，采用文献[2]方法得到的复位精准度平均值为68%，而采用所提方法得到的复位精准度平均值为87%。对比上述实验结果可以看出，所提方法的复位精准度更高。

采用不同方法进行开关电源磁芯复位实验的所需时间如图3所示。

图3 不同方法复位所需时间对比图

根据图3可知，在7次实验中，文献[1]方法的复位时间平均值为0.25s，文献[2]方法的复位时间平均值为0.45s，所提方法的复位时间平均值为0.15s。上述实验结果表明，可以发现所提方法的精准度始终保持较高状态，平均准确率达到85%以上；所提方法所需的复位时间较少，每一次复位时间没有明显差距，较为平稳，表明所提基于脉冲增益的开关电源磁芯复位方法具有一定的可靠性。

5 结论

快速准确的磁芯复位能够确保高重复率的准分子电源稳定运行。因此，本文脉冲增益基础上对开关电源磁芯复位方法进行研究。磁芯实现精准复位的关键是对复位电路的设计，通过磁芯工作过程基本原理，获取磁场强度、磁环高度等参数，结合磁芯复位电路示意图，计算电流取值范围与复位绕组两端电压值，并分析电压值与复位时间存在的联系，结合三者关系实现复位电路的设计。实验结果表明，所提方法改善了传统复位方法精准度低的缺陷，实现磁芯快速复位。