基于颗粒物堆积的混凝土路面透水砖参数模拟

范 雪，肖力光

(1. 吉林建筑科技学院交通工程学院，吉林 长春 130114；2. 吉林建筑大学材料科学与工程学院，吉林 长春 130118)

1 引言

为了延长混凝土路面使用寿命，推动海绵城市建设进程，需深入研究混凝土路面透水砖堵塞。近年来，城市化建设进程在不断提升，传统城市建设理念不断倾向于经济与社会工程，忽视了城市的生态环境保护。随着城市混凝土路面硬化程度的增加，降水汇聚量不断增加，城市径流系数明显升高，导致城市内涝问题频发[1，2]。对大量数据进行分析后可以发现，大型城市中的内涝问题逐渐加剧，严重地威胁了城市居民的生命财产安全。因此，在混凝土道路中使用透水砖有助于改善道路排水问题，降低地表径流对其的影响。透水砖是一种具有高渗透性的路面材料，其多孔隙结构具有较高的渗透性，可保证地表水形成径流渗透到地下，降低城市洪峰流量。

在透水砖的使用过程中，水中的悬浮物会造成透水砖孔隙堵塞的问题，影响其使用效果，为获取较好的应用效果，目前多使用透水砖堵塞数值仿真方法对其展开分析。例如，文献[3]提出模拟雨水下堵塞材料对透水混凝土渗透性研究方法，设计了一种应用堵塞实验方法，分析透水砖渗水性的方法，但此方法对于实验环境的要求较高，操作复杂。文献[4]提出微颗粒通过透水混凝土运动堵塞规律研究方法。利用CT技术分析透水砖渗水能力的方法，此方法操作较为简单，但过于依靠测量设备。

针对上述问题，本次研究设计新型雨季混凝土路面透水砖堵塞数值模拟仿真方法，为日后的混凝土路面维护提供技术支持，推动海绵城市的发展。

2 雨季混凝土路面透水砖堵塞数值模拟仿真方法

2.1 构建混凝土路面透水砖物理模型

本次研究中首先构建混凝土路面透水砖物理模型，为后续的数值模拟提供基础。为简化物流模型构建过程，透水砖表面粗糙度不计入物流模型中，同时，假定流程中温度均匀一致，材料物性参数为固定数值，忽略流动中的热量传递[5]。将透水砖认定为颗粒物堆积模型，砖体内部空间连通，不存在盲端孔隙，且渗透系数相同。根据砖体内部颗粒堆积规则，将砖体内部颗粒排列结构设定横向堆积与纵向堆积两类，具体内容如图1。

图1 砖体内部颗粒排列结构

由图1所示，在多孔介质的前端增设直管段，为后续透水砖的质量守恒、动力守恒以及能量守恒分析奠定基础[6]。由于在本次研究中将砖体内部热能设定为固定数值，因此在雨季混凝土路面透水砖的堵塞模拟中不计入热能转换问题，则透水砖二维流动的基础方程式设定如下

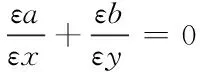
(1)

(2)

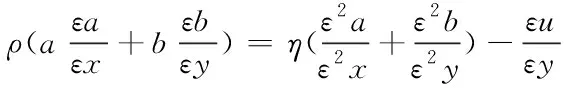
(3)

式中，式(1)为连续性方程，式(2)、式(3)为动力守恒方程。其中，x，y表示颗粒物堆积方向；ε表示能量计算系数；ρ表示颗粒物密度；η表示能量转换系数；a、b表示守恒系数。根据上述公式，构建渗水砖物理能量守恒模型。

2.2 雨水流体力学计算

以上文中构建的透水砖物理模型作为载体，计算降水后雨水流体力学数值。雨水流动时需要满足质量守恒定律、牛顿第二动力定律以及能量传输定律。设定透水砖表面积为A，控制体积为∂，面积元素为cA，根据上述设定构建雨水流体力学表达式，设定v表示雨水的流动速度。则有

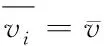
(4)

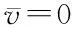
(5)

其中，cA表示计算过程中所需的面积元素。根据柯西的第一运动定律，雨水的流动定律可表示为

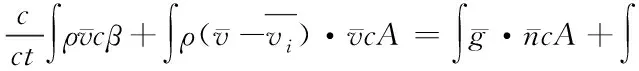
(6)

大数据通常信息繁杂，难以直接利用，需要经过分类、清洗，才能进行分析。现有文本挖掘通常采用的技术是TF-IDF加权法[14]，以突出词汇在文本中的关键性。本实验参考此方法，在分词的基础上，对高频词汇的热度进行分析。与一般的文本挖掘热点分析不同的是，本实验拟通过论文文本数据得出评价因子分析的目的，故关注的重点在于词频分析得出的词汇是否是专业词汇。专业论文词汇的词频分析应该如何做，这是一个全新的研究，没有先例可以参考，整个研究是一个不断摸索的过程。

(7)

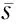
(8)

(9)

上述公式中，χ表示雨水的粘滞系数[8]；涡流粘度系数χi可表示为

(10)

将剪切力Ki产生的湍流动能与浮力Kj代入上述公式中，得到其影响模型

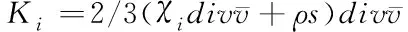
(11)

(12)

使用上述公式确定雨水的剪切力对透水砖的影响，同时得到雨水流体力学计算结果。根据上述内容，作为透水砖堵塞数值模拟过程中的边界条件。

2.3 透水砖堵塞模拟

在上文中确定了雨水的动力学计算结果，为了提升本次模拟精度，对雨水的流动状态进行判定。在本次研究中使用雷诺数表示雨水流体的流动状态无量纲数据，使用G表示此数据，则有

(13)

(14)

其中，I表示雨水流过透水砖面积；λ表示湿润范围；n表示透水砖的多孔介质缝隙度；l表示透水砖的表面积。其中，透水砖表面积可表示为

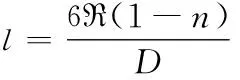
(15)

上式中，D表示透水砖介质的平均粒度；R表示颗粒物的表面形状系数。根据此数值的取值大小，确定雨水的渗流速度

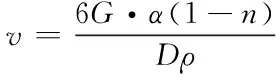
(16)

根据上述公式可得到雨水在透水砖中的流动的速度[9，10]。考虑到透水砖的材质，将透水砖中的悬浮物移动过程设定如下。将透水砖的厚度设定为x，则透水砖设定为Δx的典型单元体，则在单元时间内悬浮物的流入与流出的质量差可表示为

(17)

依据能量守恒定义，在单位时间内的悬浮物变化量相等，则在透水砖中移动的悬浮物质量可表示为

(18)

(19)

在上述公式中，T表示流体中的悬浮物浓度；Tc表示单位透水砖中介质的沉淀的悬浮物颗粒数量。在降水量保持不变的情况下，悬浮物的移动速度可表示为

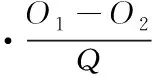
(20)

式中，ϑ表示透水砖的垂直渗透系数；O1、O2表示透水砖的上层和下层的水位变化。根据上述公式可得到悬浮物的吸附过程，则有

(21)

其中，ψ、ω分别表示透水砖的悬浮物吸附函数与解吸函数。使用上述公式可对雨水的透水砖堵塞过程展开模拟。对上文中设计的内容进行整合，至此，雨季混凝土路面透水砖堵塞数值仿真方法设计完成。

3 实验验证

3.1 实验环境

本次研究中提出了新型雨季混凝土路面透水砖堵塞数值仿真方法，本次方法设计完成后，构建相应的仿真环节对其应用效果与性能进行分析。为使本次实验中所得数据具有真实性，选择研究区域获取相应的数据为本次实验提供基础。此次研究区域处于北温带，降水量具有分配不均、年降水量变化较大、枯水时间较长，降水量一般处于700mm/a～00mm/a之间。在此环境中，选择两种不同的当前方法与新型方法展开对比。对可能出现的堵塞颗粒物组成进行分析与设定，如表1。

表1 堵塞颗粒物组成

将上述数据代入仿真软件中，作为实验数据输入仿真软件中，将其作为本次实验中主要的数据来源与依据。在本次是实验中设定了5种实验方案，每种方案中具有不同的降水流速与雨水的渗流速度，实验方案设定结果如表2所示。

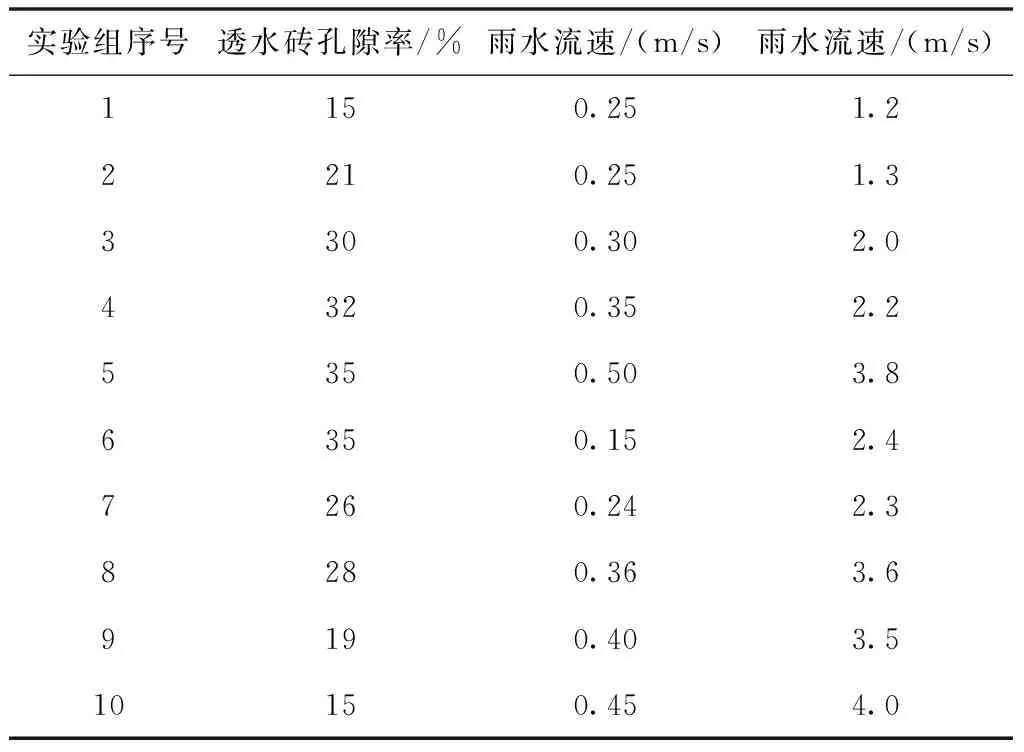
表2 仿真方案

将表2中内容作为本次实验中的主要测定内容，对上述数据进行整理与分析后，导入仿真软件中，构建相应的实验环境。

3.2 实验方案

本次实验中将主要对新型方法与模拟雨水下堵塞材料对透水混凝土渗透性研究方法、微颗粒通过透水混凝土运动堵塞规律研究方法的数值模拟仿真能力加以分析。在对大量以往案例进行分析后发现，传统模型在使用过程中存在阻塞模拟数据精度较低的问题。因此，在本次研究中将实验的对比指标设定为雨水动力学数据计算精度、透水砖渗透系数计算精度以及透水砖悬浮物吸附函数计算精度。通过上述的三组指标完成本次实验的对比过程。本次研究中涉及到的精度计算公式均采用下述公式完成。

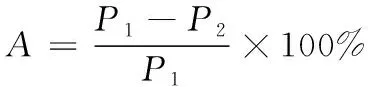
(22)

式中，P1表示获取到的正常数据仿真结果；P2表示获取到的异常数据仿真结果；A表示数值模拟精度。使用上述公式对获取的原始实验数据展开分析。

3.3 实验结果

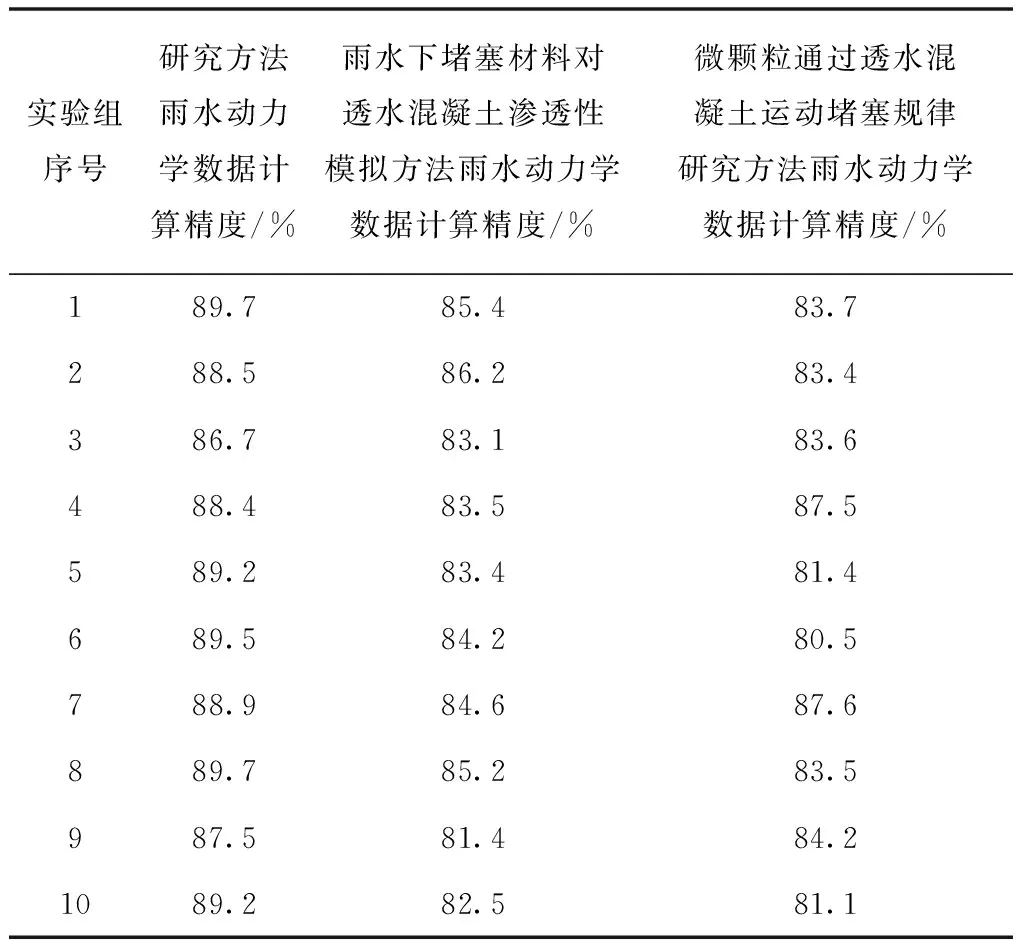
表3 雨水动力学数据计算精度

根据上述实验结果可知，在多次不同参数的数值模拟方案中，新型方法使用后所得雨水动力学数据精度较高，在多参数变化的过程中较为稳定。当前方法在过程中无法在多次参数变化的过程中得到较为稳定的雨水动力学计算结果。在对此实验结果展开分析后可以确定在数值模拟过程中使用能量守恒定律可以更好地完成数值模拟过程中的基础数值计算，从根源保证整体数值模拟的精度。对上述实验结果与分析结果进行整合后可以确定，新型方法的模拟精度较高。

图2 透水砖渗透系数计算精度

对图像中呈现的数据展开分析后发现，当前方法在使用后无法获得高精度的渗透系数计算结果。在多次实验过程中，当前方法1与当前方法2的计算结果相差较大。此种情况说明了当前方法在使用过程中不能得到可靠性较高的计算结果。为此在后续的研究中需要对其计算能力展开分析，提升数值模拟结果的可靠性。与当前方法相比，新型方法的计算精度较高，在日后的计算中可使用新型方法完成数值模拟过程。

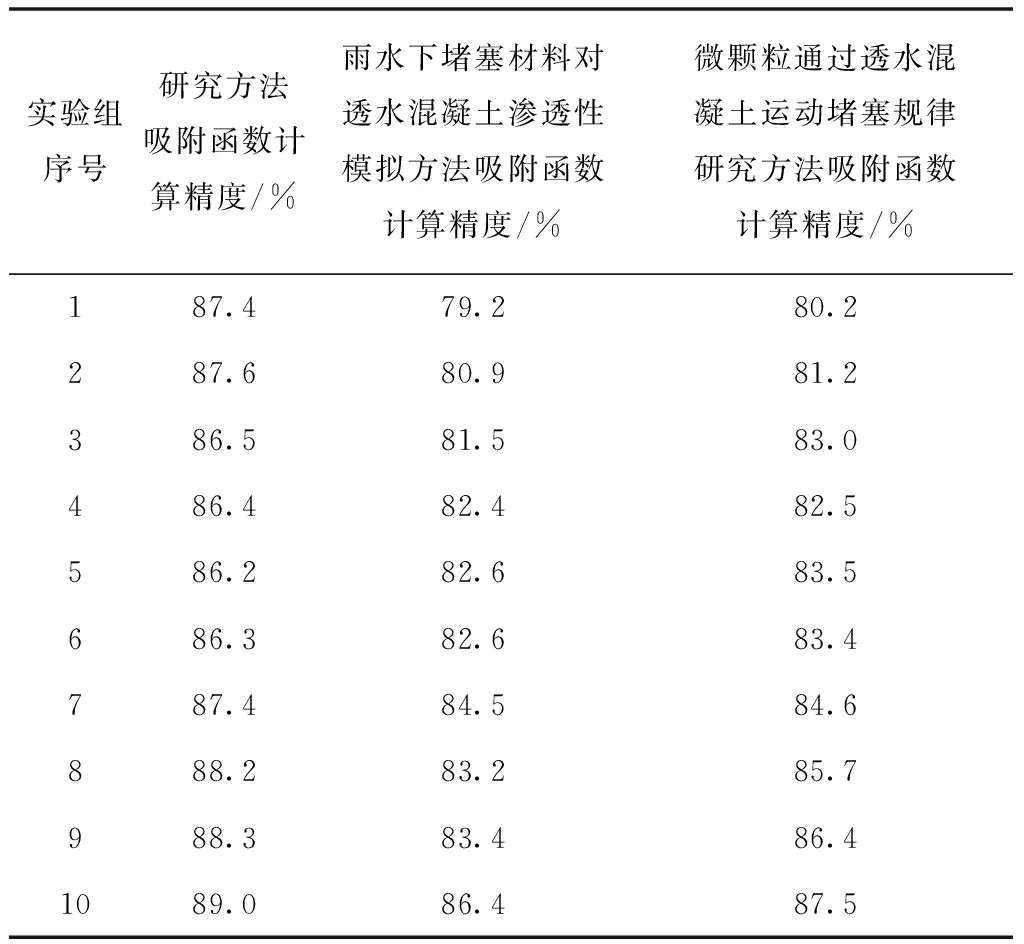
表4 透水砖悬浮物吸附函数计算精度

在本次实验中，将最后一组实验对比指标设定为透水砖悬浮物吸附函数计算精度，此函数计算结果直接影响到数值模拟方法的使用效果。对上述数据展开分析后可以发现，新型方法的计算精度明显高于当前方法。此种情况主要因为在前几个计算环节中出现了较多的计算误差，造成了此函数计算参数异常，影响吸附函数计算结果精度。在对上述实验结果进行纵向分析也可以看出，当前方法的计算精度波动较大，证实了此方法使用效果较差。由上可知，新型方法的使用效果较佳。

将雨水动力学数据计算精度、透水砖渗透系数计算精度以及透水砖悬浮物吸附函数计算精度进行综合分析后可以发现，新型方法在计算部分展开了针对性的优化，在一定程度上提升了数值模拟数据的精度与可靠性。

4 结束语

混凝土路面的堵塞率是衡量路面透水能力的关键指标之一，当透水砖堵塞后会导致混凝土路面渗流能力不断下降，降低混凝土路面的使用寿命。为了提升雨季混凝土路面维护能力，在本次研究中提出新型透水砖堵塞数值模拟方法。此方法在一定程度上弥补了当前方法的不足，提高了数值模拟方法的计算精度。但在一些环节还存在部分问题，在日后的研究中还需要对其展开优化分析，逐步提升新型数值模拟方法的使用效果。