基于深度迁移学习的电力作业安全带佩戴检测

潘志敏，王梓糠，蒋 毅，尹骏刚

(1. 国网湖南省电力有限公司检修公司，湖南 长沙 410004；2. 长沙理工大学电气与信息工程学院，湖南 长沙 410114；3. 湖南大学电气与信息工程学院，湖南 长沙 410082)

1 引言

安全一直是电力作业当中首要关注的问题，在高空作业中频发的高处坠落是电力行业最常见的安全事故之一，也是造成人员伤亡较高的事故类型，2019年电力行业发生的43起人身伤亡事故中，15起为高处坠落，占比35%。数据表明，作业人员不遵守安全操作规程，未使用或不正确使用安全带，是造成高处坠落事故主要原因。为了防止此类安全事故的出现，企业出台了相关安规政策，研究人员也对此提出了不同的解决方案[1，2]。文献[3]中提出了一种具备无线声光传感器的安全带，防止作业过程中安全带锁扣未锁紧导致的高处坠落，文献[4]对安全带悬挂器进行改进，防止挂钩变形而造成的高处坠落但这些措施都是应用在作业人员佩戴安全带之后，而无法实时确定作业中人员是否佩戴安全带。

目前国内对高空作业安全带佩戴识别的研究较少，文献[5]提出利用深度卷积神经网络(Deep CNN)来实现建筑工人的安全带佩戴检测，但该方法的准确率不足而且依赖大量的数据与计算资源。在智能交通领域，基于图像识别实现汽车安全带的检测也是目前流行的方法，文献[6]研究了利用深度学习来实现汽车安全带检测方法，较好地提升了安全带检测的准确率，同时也最大限度地减少了人为干预和手工设计特征的复杂性。

深度学习在多数情况下性能都比传统机器学习方法优异。但在实际应用过程中，深度学习存在严重的数据依赖问题以及超参数优化问题，使得深度学习难以运用到不同情境中。迁移学习是机器学习中解决训练数据不足这一瓶颈问题的重要手段[7]。目前对深度学习与迁移学习的结合也有大量的研究，文献[8]提出加入自适应层来计算源域与目标域的距离，并将其加入网络的损失训练中。文献[9]将生成对抗网络引入深度迁移学习中，降低了源域与目标域之间的分布差异，取得了良好的效果。Fine-tuning是一种简洁的深度网络迁移方法，通过微调预训练模型相关层来适应特定任务，训练时间短且准确率较高。

深度学习的性能表现对其超参数配置十分敏感，而超参数配置通常需要多次尝试才能取得较为满意的效果。目前，网格搜索、随机搜索、贝叶斯优化算法是常见的超参数调优方法。网格搜索通过在自定义多维网格上手动选择参数组，在超参数较多的情况下几乎难以使用；随机搜索在超参数取值空间随机自动生成超参数配置进行测试，不能保证找到最优超参数；贝叶斯优化算法属于序列优化方法，需要顺序执行多次，耗时较长。

本文首次将深度迁移学习应用到安全带佩戴检测中，提出三种Fine-tuning深度学习迁移方法将基于ImageNet数据集预训练的残差网络(Residual Net， ResNet)应用到自构建的作业安全带佩戴图像数据集上，提出差分动态哈里斯鹰群优化算法(Dynamic Harris Hawks Optimization with Differential Evolution， DHHO/DE)用于深度迁移学习模型的超参数优化，得到最优超参数配置与最优模型。本方法有效提升了模型预测的准确率，为相关图形检测开辟新路径。

2 基于深度迁移学习的电力作业安全带佩戴检测模型

本文提出一种基于深度迁移学习的作业安全带佩戴检测模型，具有三层结构，包括优化层、训练层以及应用层，实现深度迁移学习模型超参数优化以及安全带佩戴检测。其结构和功能如图1所示。

图1 安全带佩戴检测模型

1)优化层

提出DHHO/DE实现深度迁移学习模型的超参数寻优。将一组超参数视为一个哈里斯鹰个体，随机生成N个哈里斯鹰个体组成种群，对应N组超参数。每组超参数配置的深度迁移学习模型都将经过训练层，并且根据目标优化函数得到相应的适应度值。在种群中挑选适应度值最优的个体作为下一次迭代的目标个体，再根据公式更新个体的位置。当迭代到达最大次数或者满足评测指标时即可输出最优个体位置，对应最优超参数。

2)训练层

作业安全带佩戴训练图像集经过预处理后传入某一组超参数配置的深度迁移学习模型进行训练，随后在训练好的模型上进行测试。训练层通常会经过多次迭代，从而使模型参数趋于稳定。图像预处理包括定位、剪裁、色彩变化、角度变化等深度学习常用的图像增强方法，其目的在于增强神层神经网络学习的鲁棒性，同时在一定程度上扩充数据集。

3)应用层

在应用层中，为了实现更高准确率的佩戴检测，现场图像首先经过YOLOv3网络检测得到作业工人位置，然后将检测到的工人图像经过预处理后传入最优超参数配置的深度迁移学习模型，进行安全带佩戴检测即可得到结果。

3 深度迁移学习

迁移学习方法通过共享深度学习模型参数来解决数据量与计算资源的问题[7]，能达到较好的拟合效果。因此，本文在基于源数据集ImageNet训练的ResNet50上使用Fine-tuning微调模型结构以训练自构建的安全带佩戴数据集。

3.1 ResNet50卷积神经网络

本文提出的安全带佩戴检测模型基于ResNet50[10]构建。ResNet50中包含了49个卷积层和一个全连接层，其结构如图2所示。

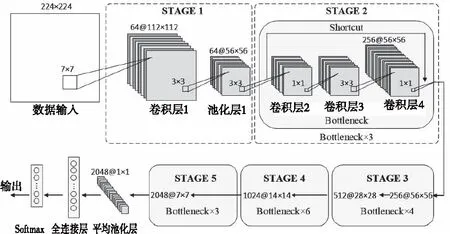
图2 ResNet50结构图

ResNet很好地解决了深度学习在层数加深时带来的梯度消失与梯度爆炸的问题，是目前学习性能最好的卷积神经网络之一，ResNet50包括5个阶段，其中STAGE1是对输入数据的卷积与池化预处理，STAGE2由3个Bottleneck块组成，Bottleneck块包含3个卷积核分别为1×1，3×3，1×1的卷积层，两个1×1的卷积核分别对输入输出数据进行降维与升维操作，较大程度的减少了计算资源的消耗。图2所示为STAGE2的第一个Bottleneck，每个STAGE的第一个Bottleneck不会对输入数据进行降维。Bottleneck块中的跨层连接(Shortcut)是ResNet拥有优异性能的根本原因，跨层连接有两种类型分别对应输入输出通道相同与不同的情况。在深度学习模型中加入跨层连接能够让深层的梯度更好的传播到浅层网络，使得浅层的网络参数也能得到较好的训练[10]。其余阶段包含13个Bottleneck块，最后输出2048维7×7的特征量经过全局平均池化后由全连接层Softmax输出。

3.2 Fine-tuning迁移学习方法

Fine-tuning微调是最为常见的迁移学习方法，通过调整预训练网络的结构可以快速的适应目标任务，并且具有较好的鲁棒性与泛化能力。针对图像的训练任务，一般会更改模型后几层以保留浅层学习好的边缘等特征。为了达到更好的迁移效果，本文提出三种Fine-tuning方法，如图3所示。

图3 Fine-tuning方法

方法1初始化全连接层参数，根据目标任务重构Softmax的输出分类，其余层参数初始化为预训练模型的参数，在训练目标数据集时，预训练模型参数也会随之微调；方法2与方法1的区别在于第一阶段到第五阶段的预训练模型参数将会被冻结，训练目标数据集时仅改变全连接层参数；方法3在方法1的基础上对STAGE5的卷积层进行初始化，引入超参数m对初始化卷积层个数进行控制，当m=0时方法3退化到方法1。超参数m取不同值时会得到不同的训练效果，因此将m加入到模型超参数优化流程中以得到最优值。

4 深度迁移学习模型的超参数优化

4.1 差分动态哈里斯鹰优化算法

本文为解决深度迁移学习存在的超参数设置困难的问题，提出一种改进的哈里斯鹰优化算法对超参数进行寻优。哈里斯鹰优化算法由Heidaria等人从哈里斯鹰的捕食行为中得到启发并于2019年提出[11]，该算法具有较强的全局搜索能力，并且需要调节的参数较少，但在实际运用中，标准哈里斯鹰算法存在搜索收敛较慢，收敛精度不高以及后期会陷入局部最优等问题。本文引入动态调整参数以及差分进化提出差分动态哈里斯鹰算法(DHHO/DE)有效提升了算法的收敛速度、精度与后期跳出局部最优的能力。

哈里斯鹰算法模仿哈里斯鹰的群体捕食行为，根据所追逐猎物的状态不同，变换捕食策略，主要由3部分组成：探索阶段、转变阶段、开发阶段。

1) 探索阶段

哈里斯鹰随机栖息在不同的位置，基于两种策略等待猎物出现，如式(1)所示

X(t+1)

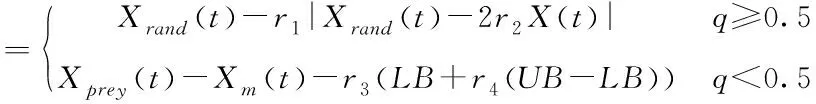
(1)

式中，X(t+1)是哈里斯鹰下次迭代t会到达的位置，Xprey(t)，X(t)分别是当前猎物与哈里斯鹰的位置，r1，r2，r3，r4与q是(0，1)之间的随机数，LB与UB是搜索空间上下界，Xrand(t)是从当前种群中随机挑选的哈里斯鹰个体的位置，Xm是当前种群的平均位置。

2) 转变阶段

哈里斯鹰根据猎物的逃逸能量E在探索与不同的开发行为之间转换，E的更新公式如式(2)所示

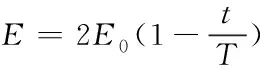
(2)

式中，E0是猎物的初始能量，当|E|<1时进入开发阶段，当|E|>1时进入探索阶段。在整个迭代过程中，|E|由2逐渐递减至0，导致在算法迭代后期始终小于1。当|E|<1时，算法不具备全局搜索能力，此时算法就有一定概率陷入局部最优解。本文在式(2)中加入动态因子η以提升算法后期全局搜索能量。

(3)

式中randn为正态分布，加入动态参数后，式(2)变为

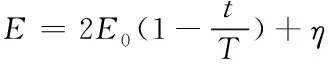
(4)

由图4可以看出，加入动态参数η的逃逸能量E在迭代后期偶尔突变使|E|>1，算法将重新进入探索阶段，从而提升算法的全局搜索能力。

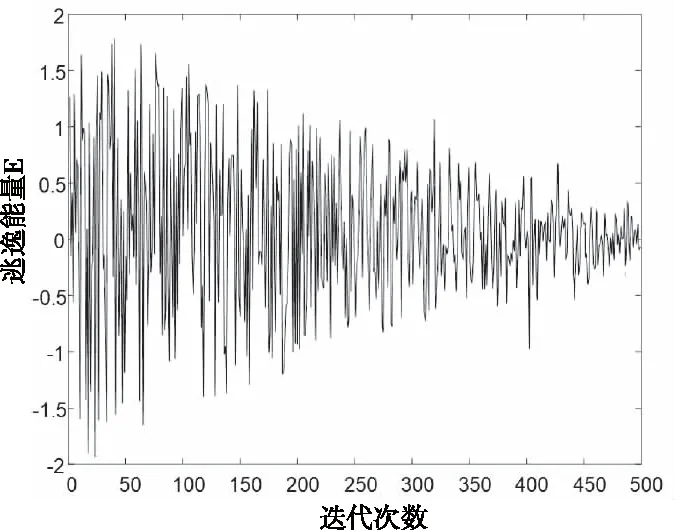
图4 加入动态参数后的逃逸能量

3) 开发阶段

定义r为猎物逃脱概率，r<0.5时猎物成功逃脱，r≥0.5表示猎物在哈里斯鹰抓捕前未能逃脱。根据猎物剩余能量不同，哈里斯鹰将执行不同的捕食策略。当r≥0.5且|E|≥0.5时，执行软围攻策略，哈里斯鹰位置更新可用式(5)表示

X(t+1)=ΔX(t)-E|JXprey(t)-X(t)|

(5)

式中，ΔX(t)是t次迭代中，猎物与鹰的位置之差，J=2(1-r5)代表猎物的随机逃亡过程。当r≥0.5且 |E|<0.5时，执行硬围攻策略，位置更新由式(6)表示

X(t+1)=Xprey(t)-E|ΔX(t)|

(6)

当|E|≥0.5且r<0.5时，猎物尚且有足够的逃逸能量，此时的哈里斯鹰位置更新可用式(7)表示

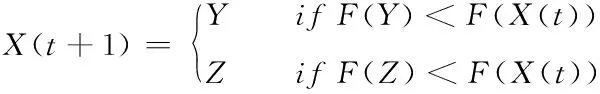
(7)

Y=Xprey(t)-E|JXprey(t)-X(t)|

(8)

Z=Y+S×LF(D)

(9)

式中，哈里斯鹰快速俯冲的数学模型表示为莱维飞行LF(χ)函数，D是需要解决问题的维度，S是1×D的随机向量，莱维飞行LF(χ)函数可由式(10)计算

(10)

式中，μ，υ是(0，1)之间的随机数，β是默认常量，设置为1.5。

当|E|<0.5且r<0.5时，哈里斯鹰执行快速俯冲式硬围攻，将式(8)更改为

Y=Xprey(t)-E|JXprey(t)-Xm(t)|

(11)

式中，Xm(t)是哈里斯鹰种群的平均位置，此时个体的位置可由式(7)、式(9)、式(11)更新。

此外，本文还对每一代的种群使用差分进化策略，以提升算法的收敛速度与精度。差分进化算法包含变异、交叉、选择3个过程。对一次迭代完成后的种群进行变异操作

Zi=Xbest(t)+F×(Xr1(t)-Xr2(t))+

F×(Xr3(t)-Xr4(t))

(12)

式中，Xr1、Xr2、Xr3、Xr4是从种群X中随机挑选的个体，F是变异尺度，Xbest(t)是第t代最优个体位置。

交叉操作从当前父代中产生一个后代，如式(13)所示

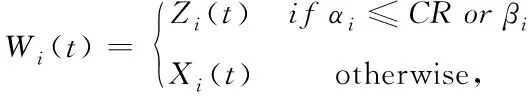
(13)

式中CR为交叉概率，βi代表[1，D]中的随机值。最后是选择操作，如果后代Wi的适应度值Fit(Wi)优于父代Xi(t)的适应度值Fit(Xi)，那么后代将替换父代，反之保留父代，由式(14)表示。

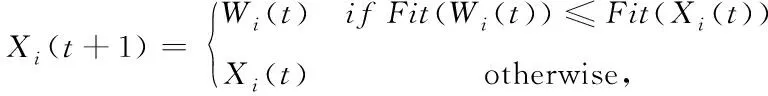
(14)

图5给出了HHO[11]、IHHO[12]、WOA[13]以及DHHO/DE在求解部分基准函数200维时的收敛曲线图，可以看出本文所提算法在收敛速度与精度上均有较大提升。

图5 基准函数收敛曲线

4.2 优化方法

h*=arg maxeval(θ|h)

(15)

式中，θ为模型参数，eval为评价函数，本文自构建的数据集正负样本均衡，因此选用准确率作为评价指标，如下式所示

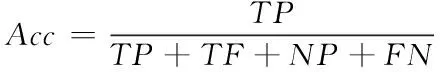
(16)

式中，TP为真正类样本，即正确检测到安全带的样本，TF为真负类样本，NP为假正类样本，FN为假负类样本。

使用DHHO/DE进行模型超参数寻优的具体过程如图6所示，首先随机生成N组超参数作为哈里斯鹰初始群体，每组超参数配置相应的深度学习模型并进行训练与测试，随后使用式(16)计算个体的适应度值，将适应度值最优个体作为目标个体，再使用DHHO/DE更新种群位置即超参数，最后使用更新后的超参数配置深度学习模型，开始下一轮迭代。满足最大迭代次数时，输出的最优个体位置就是最优超参数。

图6 超参数优化过程

5 实验与结果

本文实验数据集采用在现场拍摄的1000张电力工人佩戴安全带作业的照片作为正类样本，1000张未佩戴安全带的照片作为负类样本，各分割200作为实验的测试集，部分数据集如图7所示。

图7 部分数据集

训练实验使用的CPU为Inter(R) Core(TM) i7-7700，GPU为NVIDIA GTX 1080Ti，内存为16G，操作系统为Windows10，开发环境为Anaconda3(Python3.6，Pytorch1.2.0)。

5.1 超参数寻优

本文对深度学习中学习率(Learning rate)、优化器(Optimizer)、批量样本大小(Batch size)以及3.2节中提出的Fine-tuning超参数m进行寻优操作。学习率是模型训练中最为重要的超参数，对模型训练的精度与速度都有直接影响；合适的优化器同样也能加速模型训练，优化器参数一般都会选取固定的值，本文不作过多探讨；样本数量大小会影响到优化器的寻优效果，一般来说较大的样本数量会加速梯度下降，但容易造成内存溢出的问题。各超参数取值范围如表1所示。

表1 超参数

5.1.1 不同的Fine-tuning方法对比

初始化哈里斯鹰种群数量为N=10，优化器参数使用不同的数字对应不同的优化器。对于需要整数类型参数的超参数，在迭代最后使用Round取整将浮点数变为整数，选取Acc值作为适应度值函数。优化算法迭代50次，每一代中N个深度迁移学习模型各训练10次，算法收敛结果如图8所示。

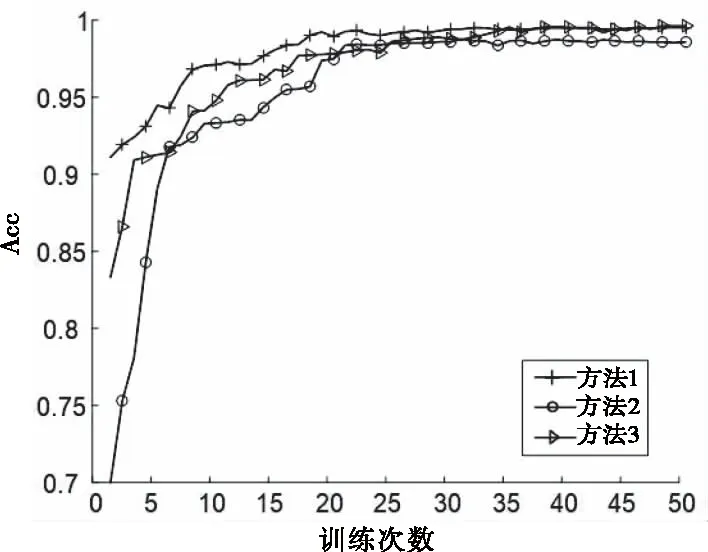
图8 三种方法寻优收敛对比

可以看出在优化算法仅迭代到20代时，三种方法训练得到的准确率已经趋于稳定，模型结构的调整有利于提升准确率但实际上会增加训练的时间。DHHO/DE寻优得到的各个方法最优超参数如表2所示。

表2 最优超参数

5.1.2 不同优化算法方法对比

为了验证本文所提优化算法的优越性，将DHHO/DE与WOA以及贝叶斯优化算法在基于方法3微调的模型上进行超参数寻优，并且进行比较，其结果如图9所示。可以看出与其它两种算法相比，本文所提算法在收敛速度与准确率上都有一定提升。

图9 不同的优化方法对比

5.2 结果分析

使用最优超参数配置预训练ResnNet50后，3种Fine-tuning方法的测试集准确率Acc与训练损失Loss如图10、图11所示。

图10 三种方法准确率对比

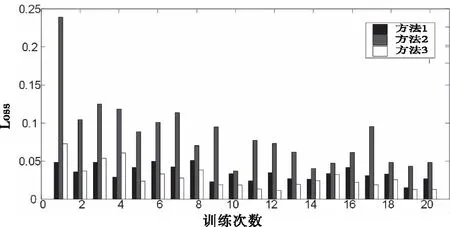
图11 三种方法训练损失对比

得益于迁移学习的特性与Fine-tuning方法的简洁，ResNet50经过仅20次训练就能得到较高的准确率。方法1、方法3的准确率能够达到0.99以上。方法2由于冻结了模型参数在前几次训练的表现不佳，但在20次训练后也能达到0.98以上的准确率，并且方法2在训练时间上比其它两种方法减少了20%。综合比较，本文选取最优超参数配置的基于方法3微调的预训练ResNet50作为电力作业安全带佩戴的检测模型。将图像输入到已训练的微调模型中，经过一个Bottleneck块处理后，输出特征如图12所示，可以看出微调模型能够较好地识别安全带特征。

图12 输出特征可视化

5.3 模型应用

在将训练好的电力作业安全带佩戴检测模型应用到作业现场时，需要考虑到工人的识别问题。目前行人识别已经是发展非常成熟的一个技术领域，本文采用预训练的YOLOv3[18]进行工人检测，将检测的工人图像传入到安全带佩戴检测模型，输出佩戴概率，如图13所示。

图13 模型检测结果

由图13 (a)可知，当工人未佩戴安全带时，检测模型输出的置信度较低，受工人穿戴衣物的影响在一定数值内波动但不会超过检测阈值；图13(b)检测模型输出的置信度较高，可以判断工人已佩戴安全带。

6 结论

为了解决电力作业安全带佩戴检测问题，本文提出了一种基于深度迁移学习的作业安全带佩戴检测方法。首先通过重构预训练ResNet50的卷积层与全连接层提出了三种不同的Fine-tuning迁移学习方法，利用迁移学习减小模型对数据集的依赖，然后针对模型超参数寻优问题，提出了DHHO/DE算法对三种方法构建的模型进行超参数优化，最后将最优超参数配置的三种模型在自构建的2000幅数据集上进行训练。结果表明本文提出的检测方法在训练集较少的情况下也能够实现准确率达99%的安全带佩戴检测。本文提出的方法为解决电力及其它行业高空作业安全检测难题提供了可行的思路。