海底电缆涡激振动流固耦合有限元建模分析

吕安强，裴琳琦

(1. 华北电力大学电子与通信工程系，河北 保定 071003；2. 华北电力大学河北省电力物联网技术重点实验室，河北 保定 071003；3. 华北电力大学保定市光纤传感与光通信技术重点实验室，河北 保定 071003)

1 引言

随着国家海洋战略的持续推进，高压海底电缆作为海上平台、岛屿与陆地大电网连接的枢纽，在电网国际化、区域电网互联等领域发挥重要作用，其安全稳定性对电力系统的正常运行至关重要[1-3]。海底电缆一般敷设于海床上或海底淤泥中，受洋流冲刷等因素影响，部分敷设段缆体会裸露，处于悬跨状态，悬跨海底电缆受到海底洋流反复冲刷会产生涡激振动，导致磨损、疲劳等现象，致使缆体产生机械损伤，影响正常工作。如果能分析海底电缆的涡激振动特性，利用分布式光纤传感技术对其进行监测，及时发现并进行处置，就能有效的防止事故的发生[4-7]。

目前，国内外学者对涡激振动的研究主要集中在海洋隔水管、输油管道等。文献[8]利用尾流振子模型和多体系统传递矩阵预测海洋热塑性增强管振动特性和涡激振动响应的动力学模型。文献[9]基于现有的钢悬链式立管出平面运动理论，提出了一个钢悬链式立管出平面涡激振动模型，实现了钢悬链式立管涡激振动与刚体转动的耦合。文献[10]采用计算流体力学模型和流固耦合计算方法，研究了含和不含两个小控制柱的圆柱涡激振动问题，并以匀流隔离缸涡激振动实验数据验证了该数值模型的正确性。文献[11]应用剪切(SST)k-e输运模型，计算了雷诺数在900-15000的低质量-阻尼情况下单自由度弹性支撑圆柱流体力。文献[12]利用尾流振子模型方法计算模型的涡激振动动力响应，并通过模型实验说明尾流振子模型方法求解管道涡激振动的可行性。文献[13]对垂直立管在均匀和线性剪切流作用下的涡激振动进行了数值研究，结果表明，随着流动速度的增加，主振型数、最大均方根振幅、主频和疲劳损伤指数均增加。文献[14]通过施加四种不同的张力来研究张力对涡激振动的影响，结果表明，施加张力越大，振动幅值越小，水动力升力系数越高。文献[15]基于尺度自适应模拟和计算结构力学对复合材料海洋热塑性增强立管涡激振动响应进行数值计算。文献[16]利用聚乙烯管缩尺模型代替海底电缆模型进行了在水流作用下的涡激振动试验，分析得到模型的振动频率、响应幅值、模态特征等数据，但是未能获得海缆各层结构的振动和等效应力。以上研究为本文工作奠定了充足的基础，但目前国内外尚无针对高压海底电缆的涡激振动问题进行流固耦合有限元建模分析的报道。

本文首次采用流固耦合有限元建模方法对海底电缆涡激振动特性进行建模和分析，确定模型的共振频率，得出海底电缆等效模型涡激振动的振动频率和振型，分析时域和频域波形特征。此种方法可以更加真实模拟洋流作用下海底电缆发生涡激振动的振动情况，为基于光纤传感的海底电缆涡激振动特性监测提供参考。

2 有限元模型的建立

2.1 海底电缆结构与参数

海底电缆的结构基本相似，本文采用JYJQ41型110kV XLPE 绝缘光纤复合海底电缆作为研究对象。该电缆由10层结构组成，由内至外依次为铜导体、XLPE 绝缘、半导电阻水带、铅合金护套、HDPE护套、沥青防腐层、PET填充条、内衬层、钢丝铠装层和外被层，结构如图1所示。导体由铜丝绞合而成；在PET填充条层，对称分布两根光单元，该光单元由聚乙烯护套和钢管构成，钢管内置8根通信用普通单模光纤，处于松弛状态；绳被层涂抹沥青；PET填充条、光单元和铠装钢丝都以绞合方式缠绕在海缆指定层[17]。海底电缆的实际尺寸如表1和表2所示。

图1 110kV光纤复合海底电缆截面结构图

表1 电缆尺寸参数

表2 PET和铜丝铠装尺寸参数

2.2 几何模型比尺和条件

根据典型的海底电缆涡激振动工况，洋流冲刷下，裸露的缆跨长度约为8m，本文对长度7.7m，即长径比(悬跨长度与直径的比值)为70的缆跨进行建模计算。由于海底电缆结构复杂、尺寸大，直接建模计算量巨大。本文采用模型相似理论[18]对缆体进行等效，利用水弹性相似模型，同时满足水动力学相似和结构动力学相似，保证等效模型和原型物理现象满足重力相似准则(Froude准则)和弹性相似准则(Cauchy准则)。

综合考虑计算量和网格划分效果，本文采用几何比尺2.75建立几何模型，建模参数和缆体原参数对比如表3所示。根据水弹性相似准则，有限元计算设置模型各层材料参数时，密度、泊松比均等于真实材料参数，真实材料的弹性模量为模型材料参数的2.75倍，对于计算结果，缆体真实形变为模型形变的2.75倍。为了更形象有效地观察缆体形变，本文以缆体直径D作为振幅的量纲参数，此外，将缆体悬跨长度表示为L，可以使缆体不同位置处的振动情况展现更加清晰。

表3 模型的仿真参数和相应原参数对比

2.3 有限元建模计算

首先，建立海底电缆几何模型，如图2所示。根据材料力学参数相似合并原则，将海底电缆简化为7层，从内到外依次对铜导体、绝缘层(合并半导体缓冲阻水带)、铅合金护套、高密度聚乙烯(合并沥青防腐层)、PET层(合并内衬层)、钢丝铠装层和外被层；根据水弹性相似模型，添加如表4所示的材料参数；根据电缆的形状特点，对模型进行网格划分，保证网格的均匀和规则。本文将海缆几层结构进行粘接运算；对缆体两端施加固定支撑载荷，以模拟实际工程中海底电缆的固定方式，并设置流固耦合交界面，用于流体对固体的流体力传递。

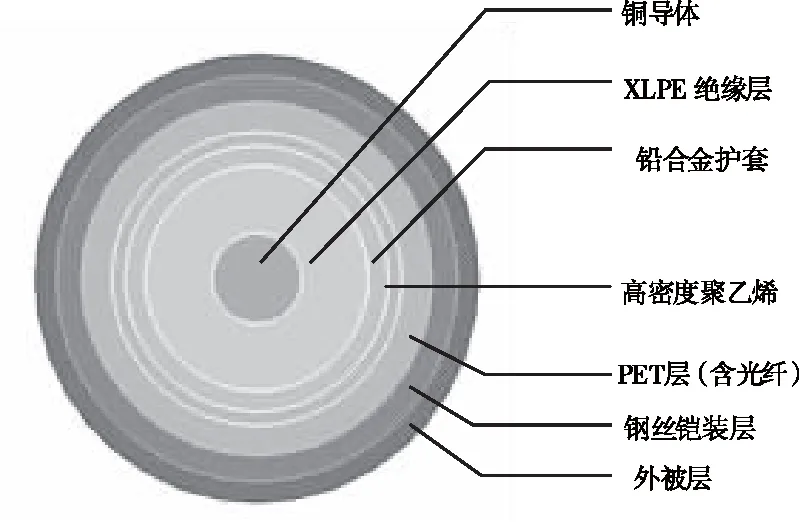
图2 简化海底电缆各层结构

表4 海底电缆等效模型材料参数

然后，建立流体域几何模型，如图3所示。建立一个长2.8m、宽0.2m、高0.14m的流体域几何模型，为了真实准确的模拟圆柱绕流靠近圆柱壁面的流体域情况，将流体域分为内流域模型和外流域模型，分别对入口、出口、上下对称面、左右壁面以及流固耦合交界面进行命名，并对流体域进行网格划分，对内流域第一层网格高度设置为4×10-5m，划分15层；根据几何模型情况和圆柱绕流理论，分别对内外流域进行网格划分，并对内流域网格进行加密，保证有限元计算的准确性，流体域网格划分效果如图3所示。在Fluent中设置流体材料为水，采用Transition SST湍流模型，时间步设为0.002s，分别计算沿图3中x轴正方向1m/s、1.6m/s、1.8m/s和2.5m/s流速下的流场情况。

最后，使用system coupling模块进行流固耦合，将每一步计算完成的流体力结果通过流固耦合交界面传递到海底电缆上，然后在mechanical模块中对缆体的涡激振动情况进行计算，实现流体和固体的迭代耦合计算。

图3 涡激振动流体域网格划分效果图

3 涡激振动有限元仿真结果与分析

为了全面准确地分析海底电缆的涡激振动特性，本文首先确定有限元模型的共振频率；然后对不同流速下的有限元模型涡激振动进行计算，并对计算结果进行分析，并与共振频率结果做对比，最后，确定海底电缆涡激振动的时频特性，为故障识别、诊断提供数据支撑。

3.1 共振频率的确定

第一步：利用湿模态分析求解海缆等效模型在水中的固有频率和振型。针对海底电缆的复杂性，根据模态基本分析理论[19，20]进行有限元计算，其前6阶模态固有频率和振型计算结果分别如表5、图4所示。由图表中数据可知，海底电缆中固有频率分布在0Hz-60Hz之间，振型主要分布在YZ和XZ平面。一二阶模态中间位置振幅最大，振型关于中间位置对称；三四阶模态1/4L、3/4L处振幅最大，振动方向相反；五六阶模态振型在1/6L、1/2L、5/6L处振幅最大，振型关于中间位置对称。

第二步：根据固有频率的计算结果进行声学谐响应分析(即海底电缆在水中的谐响应分析)，确定海底电缆等效模型共振发生时的频率。根据湿模态分析得出的固有频率结果，对电缆进行声学谐响应分析，计算结果如图5所示，模型的一二阶共振频率为11Hz，49Hz，与模态分析的第一二阶和第五六阶固有频率接近，可与涡激振动共振发生时的频率做对比。

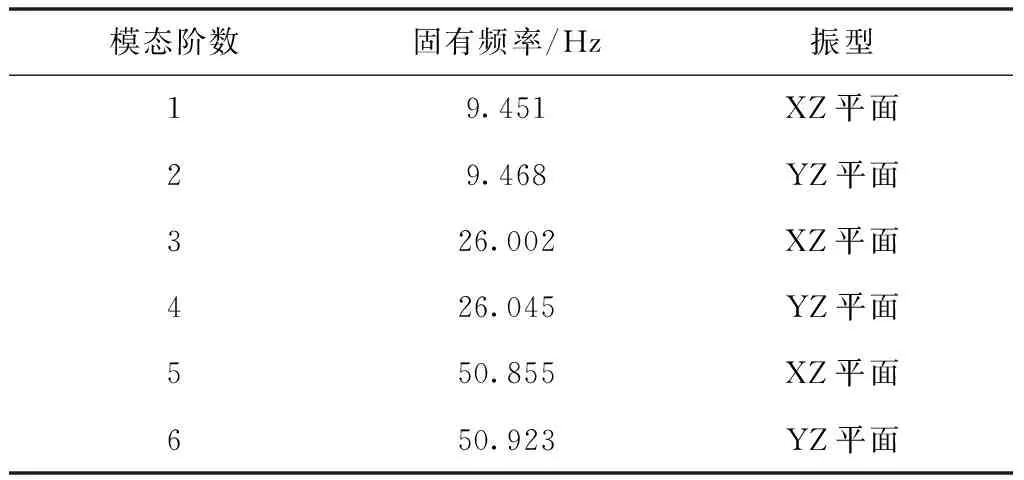
表5 模型湿模态各阶频率

图4 海底电缆湿模态振型图

图5 声学谐响应分析结果图

3.2 流体域有限元计算结果分析

当稳定流速的洋流经过海底电缆时，尾流区会形成稳定的交替泄放旋涡，旋涡的脱落会给缆体在横向(即垂直于来流的Y轴方向)向上或者向下的力，导致缆体呈周期性振动。如图6所示，为1m/s流速下的旋涡脱落云图，由图可知，前一个旋涡的脱落即将完成，下一个旋涡即将形成，圆柱下表面水流流速大于上表面流速，下一个旋涡的脱落将给圆柱一个向下的力。

图6 1m/s流速下流体域旋涡脱落云图

要分析涡激振动，首先需要对流体域的计算结果进行分析，根据圆柱绕流的理论，通常利用以下几个常见流体相关公式来分析流体域计算结果的准确性。

(1)

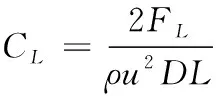
(2)

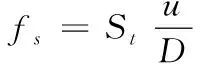
(3)

式中：CD、CL分别为缆体阻力系数、升力系数是缆体顺流向(即来流的x轴正向)和横向受力大小的无量纲参数；FD、FL分别为流体对缆体的阻力、升力；u、L为来流速度和缆体的长度；St为strouhal数，一般在0.2左右；fs为漩涡脱落的频率，可以通过对升力系数时域历程作FFT变换得到。

图7、图8为1m/s、1.6m/s、1.8m/s以及2.5m/s四种不同流速下圆柱升力系数要和阻力系数的频域图。图中可知，同一流速下，阻力系数频率均为升力系数频率的2倍。1m/s时的升力系数功率谱密度最大，约为1(Pa)2/Hz，1.8m/s时的阻力系数功率谱密度最大，约为1.7×10-4(Pa)2/Hz，升力系数功率谱密度比阻力系数大4个数量级。

图7 不同流速下升力系数频域图

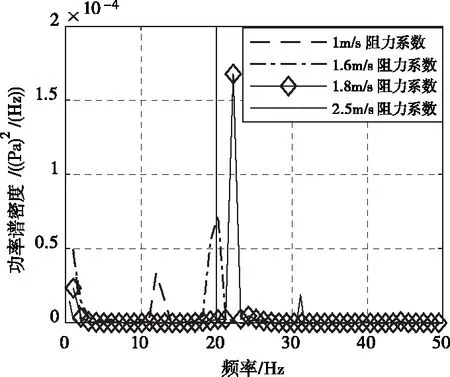
图8 不同流速下阻力系数频域图

根据上述各流速升力系数频率计算结果和计算公式，几个流速下strouhal数稳定在0.24左右，升阻力系数频率、幅值均符合流体计算理论值，证明流体域的计算结果准确，为固体域海底电缆涡激振动的计算提供基础。由计算结果可知，升力系数振幅远远大于阻力系数振幅，因此涡激振动横向振动振幅远远大于顺流向振动，因此研究海缆涡激振动特性主要考虑横流向振动对缆体的影响，因此本文将主要分析海缆横流向的涡激振动。

3.3 海底电缆涡激振动分析

3.3.1 不同流速下海底电缆涡激振动特性分析

为了更加全面的得到海底电缆的涡激振动特性，本文将对不同流速下海底电缆发生涡激振动的振动频率、振幅和振型三种振动特征进行分析。

图9 1.6m/s流速下海底电缆涡激振动振型云图

图9为1.6m/s流速下海底电缆发生涡激振动时，2.772s时刻缆体变形的振型云图，由图可知，海底电缆涡激振动的振型分布为一阶振型，变形情况沿轴向先增大后减小，两端变形小，中间位置变形最大，变形关于缆体中间位置对称，最大变形为0.425D。

在缆体最外层沿轴向1/8L、1/4L、3/8L、1/2L、5/8L、3/4L和7/8L处的振动情况提取出来进行分析。提取1.6m/s流速下1/2L处横向振动数据，如图10所示。由图可知，经过1.3s左右振动达到稳定，振动频率为10Hz，振幅为0.42D左右。图11为1.6m/s流速下各位置的振动频谱，由图可知，各点振动频率相等，均为10Hz，1/2L处振幅最大，振动幅度关于1/2L处对称，连接各功率谱顶点，即可获得海底电缆的一阶模态振型。

图10 1.6m/s流速下1/2L处横向振动时域图

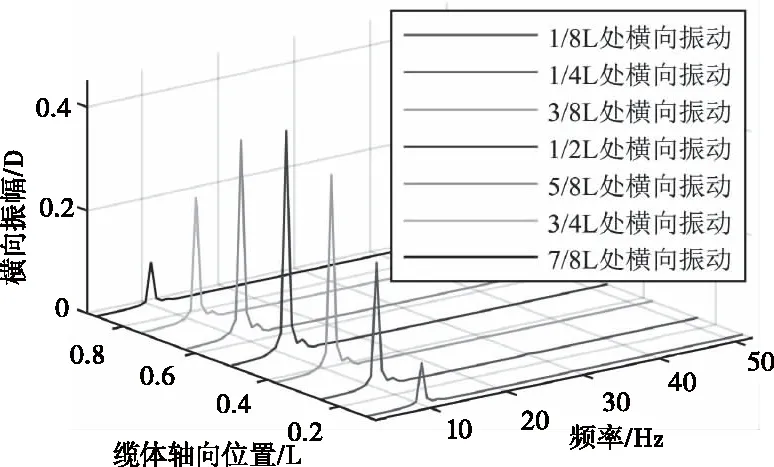
图11 1.6m/s流速下电缆各处横向振动频域图

表6为不同流速下，涡激振动达到稳定后，振幅和频率表，图12为不同流速下，涡激振动最大振幅时刻整体横向的振型情况。由图表可知，流速为1m/s时，横向变形最小，中间位置振幅为0.014D，当旋涡脱落频率接近于海底电缆的一阶共振频率时，如图中1.6m/s、1.8m/s流速下，旋涡脱落频率分别为10.1Hz、11.1Hz，接近于一阶共振频率11Hz，缆体的振幅会突然增大，1.6m/s、1.8m/s时，缆体振动稳定时，横向振幅分别为0.42D、0.65D，此时产生了涡激振动的共振现象，当旋涡脱落频率小于或大于海缆的固有频率时，振幅大约在0.13D左右。四种流速下，缆体的振型均为一阶模态振型，振动频率与升力系数频率相等。发生涡激共振时，横向涡激振动振幅远大于非共振下的振幅，因此涡激振动造成的疲劳现象主要是由横向涡激共振引起的。

表6 涡激振动振幅和频率表

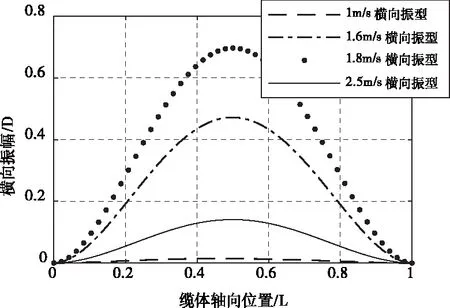
图12 不同流速下电缆沿y轴方向振型图

3.3.2 涡激共振流速下海缆的应力分析

当缆跨长期有涡激共振发生时，海缆铅合金护套有疲劳开裂风险。图13为1.8m/s流速下电缆产生涡激共振时的铅合金护套应力云图，由图可知，铅合金护套两端等效应力最大，电缆中间点振动幅度最大受到等效应力也较大，实际工程中，可以根据应力时空分布数据对缆体进行疲劳损伤和寿命的分析与计算。

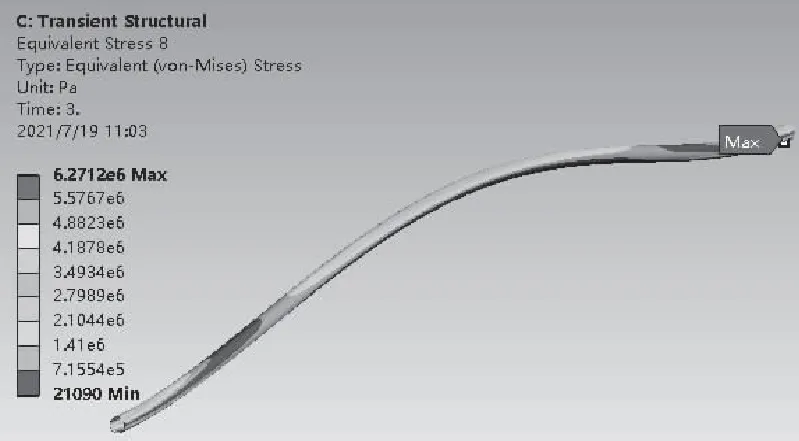
图13 铅合金护套等效应力

4 结论

本文构建了110kV海底电缆涡激振动的有限元等效模型，通过对不同流速下涡激振动情况的分析，获得了海底电缆涡激振动的振动特性，得出以下结论：

1)采用模型相似理论可以用较少的计算量完成复杂结构海底电缆的流固耦合有限元计算，计算结果与理论分析一致。

2)利用流固耦合有限元分析法可以更有效获得海底电缆各层结构的振动数据，结合时空频分析可以获得缆体振动时的特性。

3)本文研究获得了缆体的固有频率、共振频率、涡激振动振型和频率分布，这些振动数据为在实际工程中利用分布式光纤传感技术监测海底电缆涡激振动提供了高效准确的分析方法和数据支撑。

4)本文采用模型相似理论结合流固耦合有限元计算复杂结构在流体下振动的方法，可以推广应用至风机叶片、飞机螺旋桨、轮船螺旋桨等的振动分析。