Burgers方程的广义精确解*

赵 临 龙

（安康学院数学与统计学院，陕西 安康 725000）

0 引 言

1948年，欧美学者Johannes Burgers首先用模型

（其中α＞0为耗散系数）描述流体中的湍流，该方程为描述对流-耗散流之间相互影响的原始模型.这个方程被人们以Johannes Burgers的名字命名为“Burgers方程”［1］.

Burgers方程模型在等离子物理、非线性光学、量子理论和通信技术等领域占有重要的地位和作用，引起数学和物理学专家的高度关注，寻求方程（1）的精确解一直是一个重要的研究课题.2005年，石玉仁等［2］将双曲函数法进行扩展，找到了变系数Burgers方程在一定条件下的若干精确解；2007年，谢元喜［3］基于Hopf-Cole变换法和试探函数法的基本思想，引入变量变换，最终将Burgers方程化为Euler方程，利用数学软件给出相应的精确解；2017年，林府标［4］利用李群理论中的伸缩变换群，将Burgers方程化为Riccati方程，给出特殊的Riccati方程的解；2019年，蒋桂凤［5］利用试探函数法，将Burgers方程化为Riccati方程，针对特殊的Riccati方程给出相应的解形式.

目前虽然已经提出了许多方法，但需要深入探讨的问题依然很多.一种有效方法是将Burgers方程转化为Riccati方程求其精确解，但由于Riccati方程的不可积性，使该问题又成为新的探讨问题.现对相关文献中转化的Riccati方程所给出的特殊解，进行讨论给出其广义的解，以扩大Burgers方程的应用范围.

文献［6］将Burgers方程（1）的求解，化为求以下Riccati方程的精确解

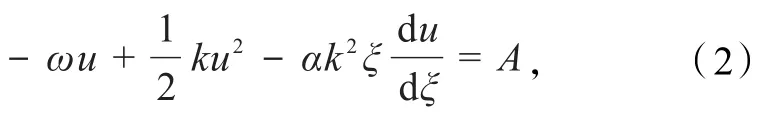
式中：k、ω分别表示波数和圆频率，A为积分常数.取A=0，方程（2）转化为Bernoulli方程，并且将其化为一阶线性微分方程

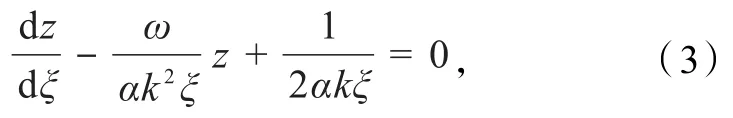
式中：ω、k为常数，然后由方程（3）的解，给出方程（2）的解为

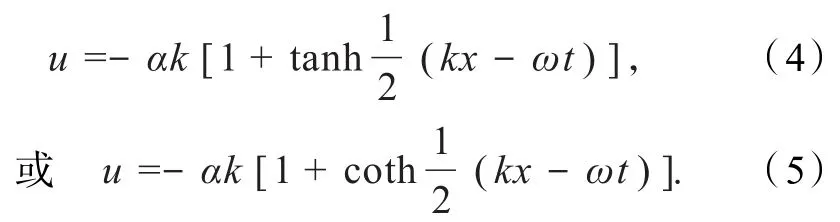
现在，对于A≠0，讨论Riccati方程（2）的精确解.

1 Riccati方程可积性理论

1998年，赵临龙［7］提出 Riccati的不变量概念，并且利用不变量概念，相继给出Riccati的解法［7-9］.

定义［9］对于Riccati方程

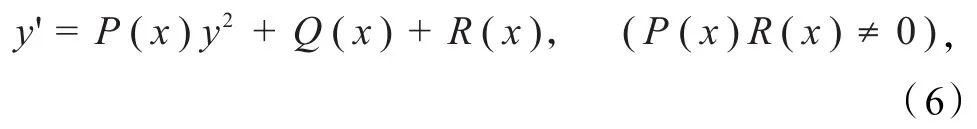
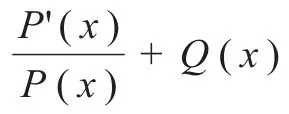
定理［9］在方程（6）中，如果存在常数α、β、γ，以及函数y0(x)和可导函数G(x)（其中G(x)≠0），满足不变量关系：

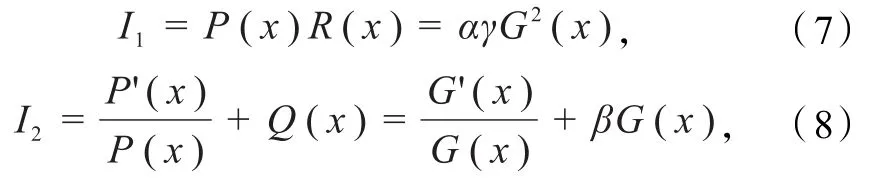
则方程（6）经线性变换

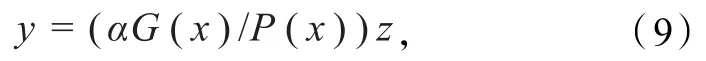
化成积分形式

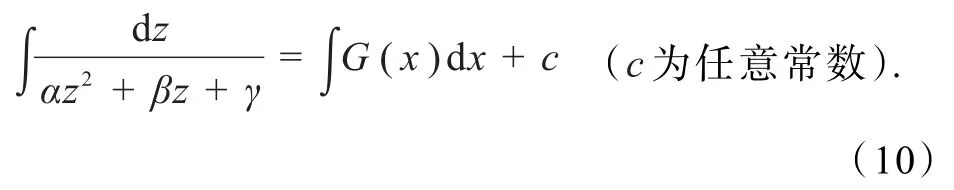
2 Riccati方程（2）解情形分析

现将方程（2）化为

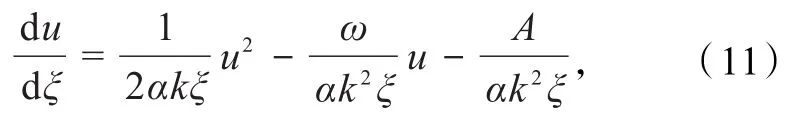
式中：ω、k、A为常数.

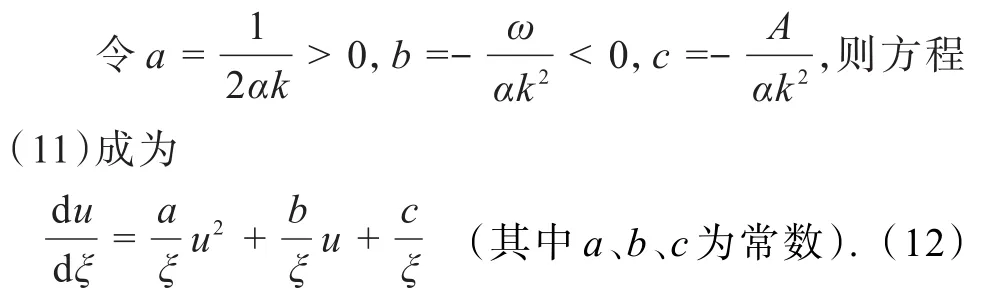
对于Riccati方程（12），由于

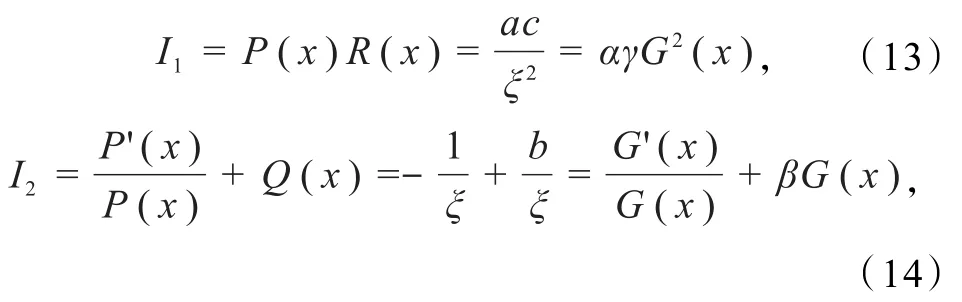
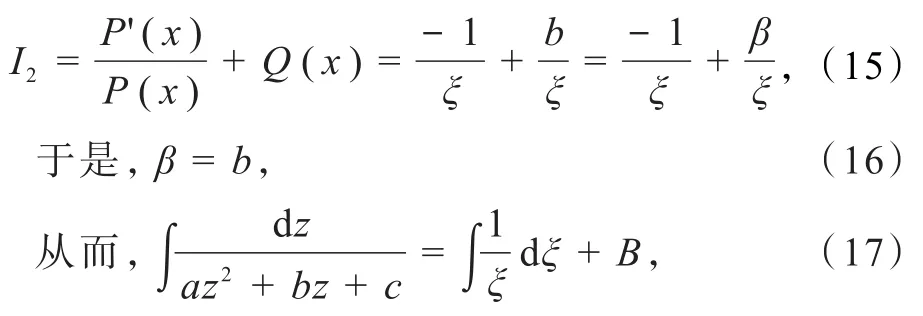
式中：a、b、c、B为常数.

（1）当Δ=b2-4ac=0，即4ac=b2＞0(a＞0，c＞0)时，有：

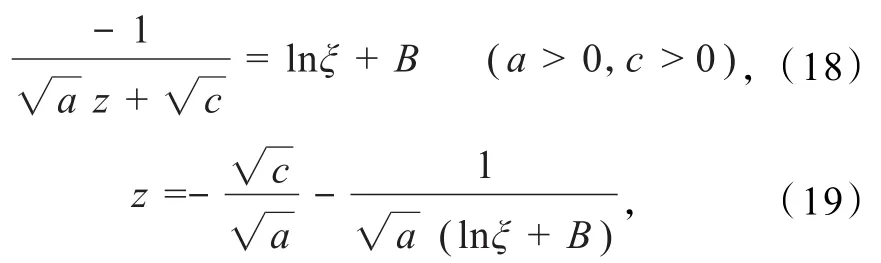
于是，由方程（9）变换关系u=(αG(x)/P(x))z，得到方程（11）的解为

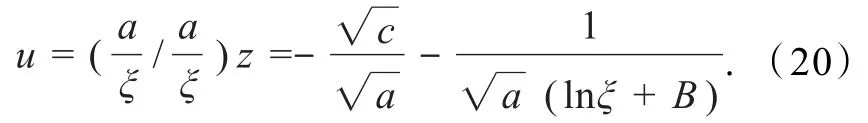
（2）当Δ=b2-4ac＞0，即4ac＜b2(a＞0)时，有

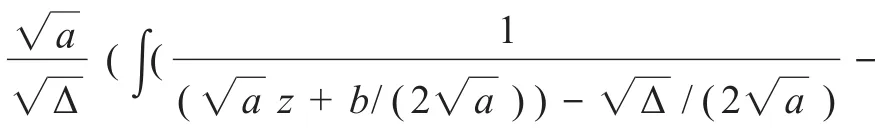
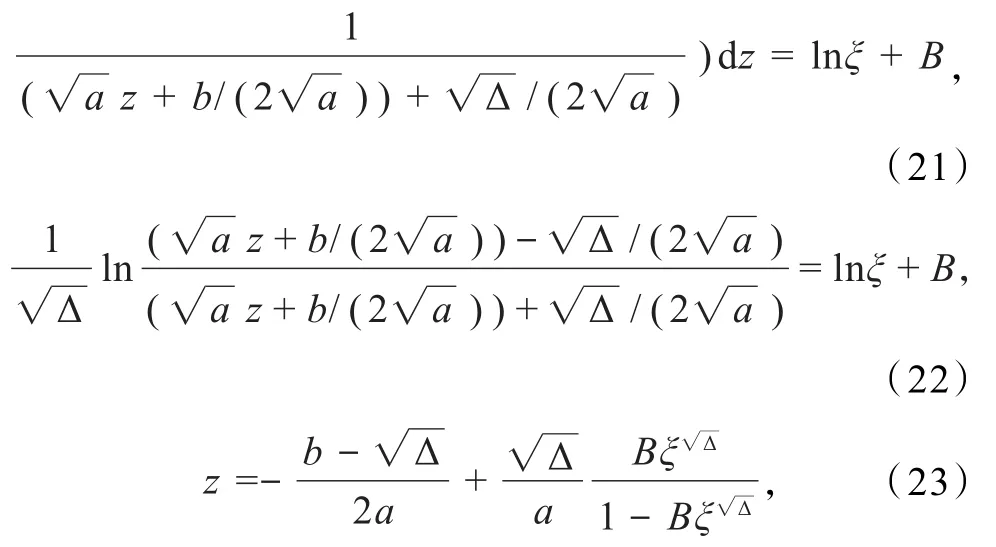
于是，由方程（9）变换关系：u=(αG(x)/P(x))z，得到方程（11）的解为

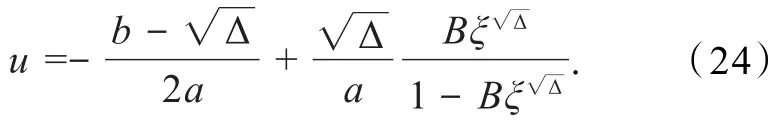
（3）当 Δ=b2-4ac＜0，即 4ac＞b2＞0(a＞0，c＞0)时，有

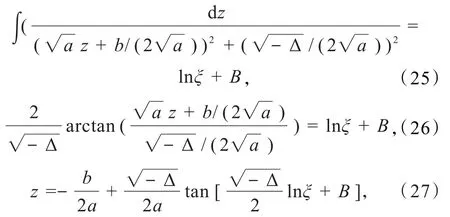
于是，由方程（9）变换关系u=(αG(x)/P(x))z，得到方程（11）的解为

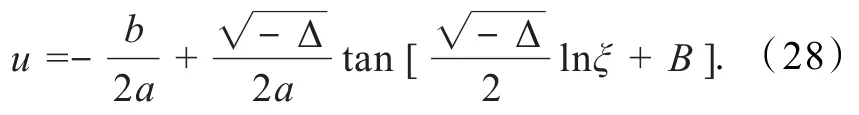
3 结 果

综上，给出Riccati方程（11）解的情形.

情形1 当4ac=b2＞0(a＞0，c＞0)，则

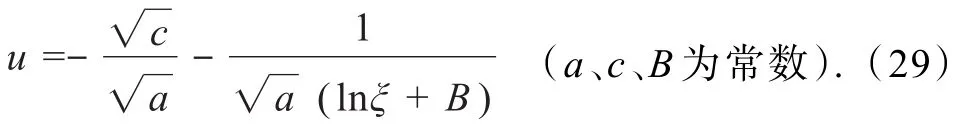
情形2 当4ac＜b2(a＞0)，则

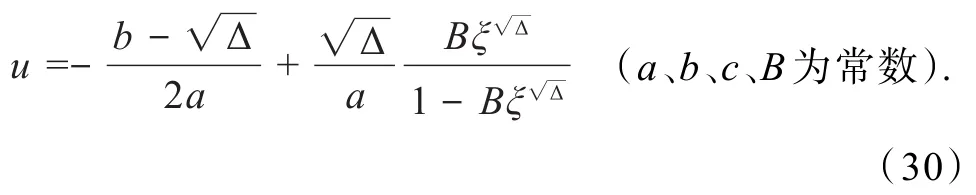
情形3 当4ac＞b2＞0(a＞0，c＞0)，则

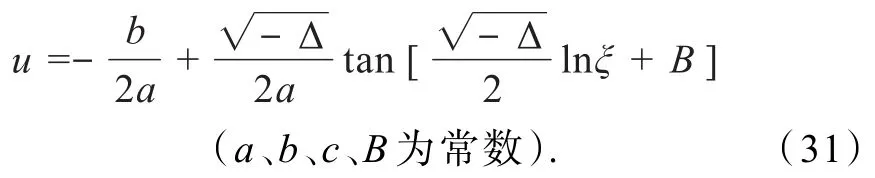
可见，利用Riccati方程（11）求解Burgers方程（1）关键取决于Riccati方程（11）的可积性.因此，对于Riccati方程（11）的研究仍然是一个很值得探讨的问题.