考虑缓冲回路的HVDC系统状态空间模型与求解算法

李志显，李 欢，刘崇茹，郑 乐，魏 伟，喻建瑜

考虑缓冲回路的HVDC系统状态空间模型与求解算法

李志显1，李 欢2，刘崇茹1，郑 乐1，魏 伟2，喻建瑜1

(1.新能源电力系统国家重点实验室(华北电力大学), 北京 102206；2.直流输电技术国家重点实验室 (南方电网科学研究院有限责任公司), 广东 广州 510663)

为了提高基于状态空间法的高压直流输电系统仿真计算精度，提出了一种考虑缓冲回路的HVDC系统仿真计算方法。以晶闸管的阀电流和缓冲电流作为状态变量对晶闸管进行建模，将换流变压器不同工况下的电压变换关系通过关联矩阵表示为统一的形式，建立换流器和换流变压器的状态空间模型，结合直流线路模型推导HVDC系统一次设备状态空间表达式。进一步，分析了控制系统的触发信号生成方法以及一次系统与控制系统的数据交互过程，实现了HVDC系统数学模型高精度求解。最后将Matlab实现的算法结果与PSCAD仿真结果进行对比，一次系统求解精度可达99.99%。

高压直流输电；状态空间；缓冲回路；缓冲电流；电磁暂态仿真

0 引言

高压直流输电以其可实现交流电网的异步连接、控制灵活性强等特点正得到快速发展和广泛应用。特别是随着大范围能源优化配置、大规模可再生能源发电并网等需求的扩大，直流输电工程项目得到快速实施[1-3]。

高压直流输电(High Voltage Direct Current, HVDC)系统的详细模型采用准稳态方程，这难以准确描述换流站附近的不对称短路故障所引起的HVDC动态行为以及逆变器交流侧不对称故障或换流变压器饱和可能引起的换相失败故障[4]。在准稳态模型的基础上，引入动态相量法进行HVDC解析建模，用开关函数表示桥臂开关状态，仿真精确程度介于准稳态模型和电磁暂态仿真模型之间[5-6]。电磁暂态仿真通常用来分析HVDC系统发生故障时的暂态响应过程和具体控制特性，当要求得到考虑换流阀的HVDC准确时域响应时，需要使用较小的积分步长，计算速度慢[7-10]。为了提升仿真速度，文献[11-13]提出建立结构化子系统线性状态模型来准确描述HVDC输电系统，并通过联接矩阵将各子系统互联构建全系统线性化建模的方法。为了追求更高精度同时解决计算规模问题，文献[14-16]提出了一种采用状态空间法求解HVDC系统数学模型的解析算法，模型可精确到阀级，计算速度快于电磁暂态仿真。

然而，目前状态空间法建立直流系统模型没有考虑缓冲电路，会使晶闸管关断时直流电流仿真结果存在较大误差。当缓冲回路时间常数大于仿真步长时，缓冲电流在阀关断期间的突变峰值会在交直流回路的电感上产生不可忽略的感应电压，尤其对于直流回路来说，感应电压会随着周期叠加，因此计算过程中缓冲回路的暂态特性不可忽略。

本文提出了一种高精度HVDC系统状态空间模型，有以下两个主要特点：

1) 以阀电流和缓冲电流作为状态变量对晶闸管进行建模，更贴近晶闸管元件特性，模型精度更高，并且可以模拟换流站闭锁等工况。同时计算结果数值稳定性比较高。

2) 将换流变压器不同工况的电压变换关系通过关联矩阵概括为统一形式，通过晶闸管等效电阻阻值的改变更新工况，参数矩阵不随工况变化而发生改变。

1 考虑缓冲回路的HVDC状态空间模型

1.1 考虑缓冲回路的换流阀数学模型

换流阀是用晶闸管元件以及相应的电子电路、阻尼回路等器件组装而成的换流器桥臂[17]，由晶闸管和缓冲回路并联而成，结构如图1所示。当晶闸管导通时，阀臂电阻为零，阀电流为输入的交流电流，缓冲电路无影响。当晶闸管关断时，阀臂电阻为无穷大，电容充放电过程产生了缓冲电流，会流进交流回路和直流回路，在交直流回路的电感上产生感应电压，尤其对直流回路来说，感应电压会随着周期叠加，影响了直流电流的准确度。为了解决以上问题，建立了缓冲回路的状态空间方程。

图1 换流阀结构

阀电压可用状态变量阀电流和缓冲电流表示为

缓冲回路电流满足基尔霍夫电流定律，缓冲回路状态空间方程可列写为

1.2 换流变压器和换流器的数学模型

换流器模型的状态方程是时变的，若要囊括所有工况，必须反复重新形成状态方程。本文以12脉波HVDC系统整流侧为例介绍建立状态空间模型过程，逆变侧同理。

12脉波HVDC输电系统整流侧在正常运行的情况下存在12个导通运行工况和12个换相运行工况。本文将变压器阀侧线电压按不同联结方式分块表示，整流器视为两个6脉波换流器在直流侧串联，通过关联矩阵计算出每一个工况下变压器的阀侧线电压、线电流，然后在求解过程中通过更新阀电阻阻值进入不同工况，从而获得微分方程系数不随工况改变发生变化的状态空间模型。

图2 整流侧换流变压器

用换流阀的阀电压表示变压器阀侧线电压，有两种表示方法。

1) 采用阀1、3、5时

2) 采用阀2、4、6时

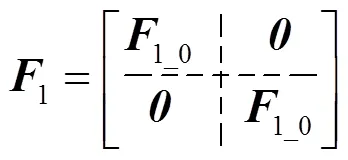
其中：

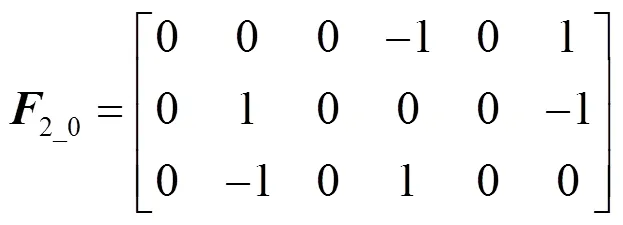
式(6)和式(7)通过阀电压表示了整流侧所有工况下的变压器阀侧线电压。

将整流侧和逆变侧换流变压器的电压变换关系整理为统一形式：

变压器阀侧电流可用晶闸管的阀电流表示：

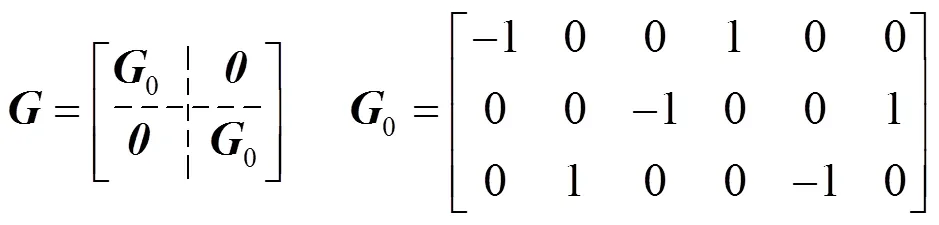
将式(1)、式(6)、式(7)、式(9)代入式(5)，可得换流变压器和换流器的状态空间模型为

1.3 直流线路模型

直流线路模型应根据实际情况进行建模，直流线路模型与交流线路模型没有本质差别，因此对应的等效线路模型均可用[18]，列写电压电流关系微分方程即可。

本文以国际大电网会议直流输电标准系统的直流线路模型为例进行建模，所对应直流线路的状态空间表达式为

整流侧和逆变侧的直流电流可用阀电流表示，有四种表示方法(以整流侧为例)。

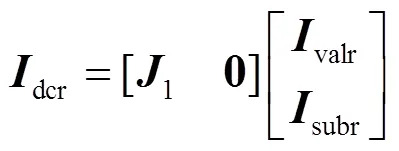
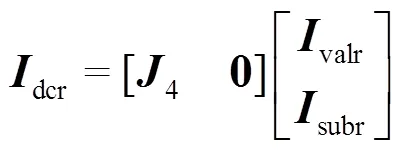
整流侧和逆变侧的直流电压也可用阀电压来表示，每一极有三种表示方法，避免冗余方程，这里仅用阀1、4来表示。

式(12)—式(16)中的各参数矩阵详细为

将式(12)—式(16)代入式(11)，可得

根据式(1)将阀电压用状态变量表示，可得直流线路的状态空间模型为

1.4 主设备系统状态空间模型求解

结合式(2)、式(10)和式(18)，生成状态空间如式(19)。

用梯形积分法对全系统状态空间表达式进行离散化处理，对式(19)两侧同时积分可得

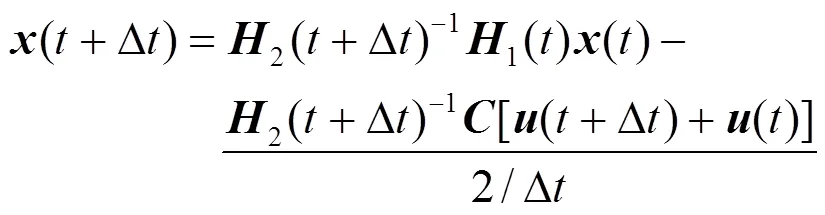
2 模型求解

2.1 触发角计算

图3 整流侧控制系统框图

图4 逆变侧控制系统框图

2.2 触发信号生成

图5 锁相振荡器控制框图

2.3 控制系统与主设备的交互过程

由图6介绍的主设备与控制侧的数据交互逻辑，可得本文算法流程框图。算法流程框图如图7所示。

图6 一次系统与控制系统的数据交互

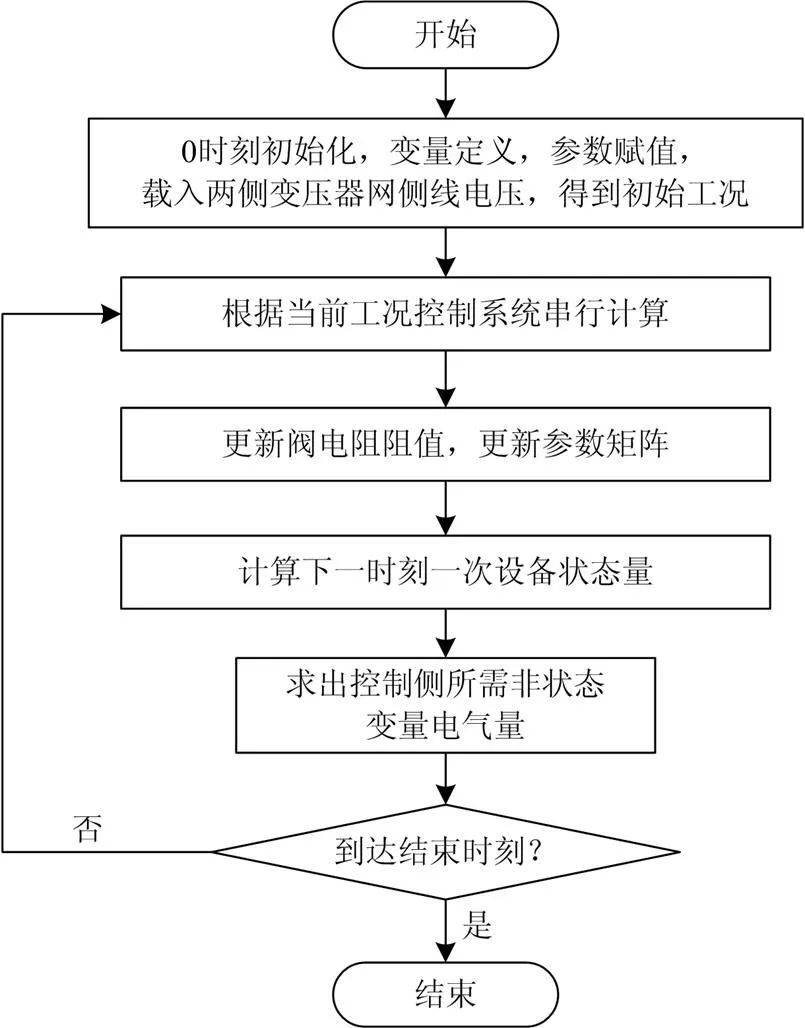
图7 HVDC系统状态空间模型计算流程

3 算例与分析

本文仿真采用的是基于PSCAD的国际大电网会议(International Council on Large Electric systems, CIGRE)直流输电标准系统[20-21]，主设备系统结构图如图8所示，包括整流侧换流器模型、直流线路模型和逆变侧换流器模型三部分，忽略直流滤波器。

图8 双端12脉波HVDC主设备系统结构

表1 标准算例系统参数

本文模型采用换流站网侧母线电压作为输入，通过Matlab的计算结果和PSCAD的仿真结果进行对比，从而验证考虑缓冲回路的HVDC系统状态空间模型的有效性和准确性。

3.1 缓冲回路对比仿真

由图9分析可知，阀电压在阀关断期间发生多次突变，这也导致了缓冲电流的多次突变峰值，而缓冲电流会流进交流回路和直流回路，在交直流回路的电感上产生感应电压，即突变峰值的导数，数值很大，尤其对直流回路来说，感应电压会随着周期叠加，因此缓冲回路不可忽略。

3.2 稳态响应

在稳态运行条件下，HVDC系统整流侧状态变量、逆变侧状态变量和直流线路中点电压波形如图10所示。

由图10中稳态响应的波形对比可知，本文算法与PSCAD仿真结果重合度较高，现将相对误差数值列于表2。

表2 稳态响应相对误差

3.3 故障响应

为了得到本文所建模型在故障发生时的暂态响应，故障分别设置为对称故障、非对称故障和直流系统双极闭锁。对称故障的设置为逆变侧换流母线在2 s时发生三相短路接地故障，电压跌落至0.7 p.u.，1 s后故障清除。非对称故障的设置为2 s时逆变侧换流母线A相发生经阻抗接地故障[22]，1 s后故障清除。闭锁工况的设置为系统启动1 s后整流器和逆变器均发生闭锁故障，且故障不清除。将PSCAD中CIGRE BENCHMARK模型故障的换流变压器网侧线电压幅值作为本文所建模型的输入变量，最后得到本文与PSCAD整流侧直流电流、直流线路中点电压以及逆变侧直流电流波形对比，如图11、图12所示。模拟闭锁工况是将PSCAD中CIGRE BENCHMARK模型稳态下的换流变压器网侧线电压幅值作为本模型输入变量，得到闭锁工况的波形对比，如图13所示。

图11 对称故障下的暂态响应

图12 非对称故障下的暂态响应

对称故障和非对称故障响应观测量选用整流侧直流电流和逆变侧直流电流，而不用阀电流、缓冲电流进行对比的原因是：由前文直流线路建模可知，整流侧直流电流和逆变侧直流电流均用阀电流、缓冲电流表示，精度相同，且选用整流侧直流电流和逆变侧直流电流更能直观地反映直流部分的暂态过程。

由图11—图13波形对比可知，本文算法在暂态响应下与PSCAD仿真结果重合度仍然比较高，现将对称和非对称故障响应相对误差数值列于表3。

表3 故障响应相对误差

由系统两种状态下得仿真对比结果可知，无论是稳态响应还是故障响应，本文模型的状态变量、系统其他电气量波形与PSCAD对比几乎重合，计算结果与PSCAD十分接近。本文所建模型状态变量在0～3 s内的最大绝对误差在10-6kA以下，直流线路中点电压最大绝对误差在10-4kV以下，在模型精确到阀级的基础上，提高了计算精度。经分析可知，主要优势在于采用阀电流和缓冲电流作为状态变量。状态变量包含24个阀电流、24个缓冲回路电流，是文献[14]中的大约4倍，对于晶闸管的描述更贴近于PSCAD软件，结果相较于文献[14]更精确。

4 结论

本文通过分析并推导出了考虑缓冲回路的高压直流输电系统状态空间数学模型，实现了该模型的高精度求解，可以得出以下结论：

1) 当缓冲回路时间常数大于仿真步长时，需要考虑缓冲回路暂态特性。以晶闸管的阀电流和缓冲电流为状态变量，实现了对考虑缓冲回路的HVDC输电系统状态空间模型的求解，一次系统求解精度可达99.99%，同时计算结果数值稳定性高。证明了本文模型能够有效提高状态空间解析法的计算精度、减小误差。本文模型模拟闭锁工况拟合程度较高，为进一步研究其他故障情况下考虑缓冲回路的状态空间计算打下基础。

2) 换流器切换不同工况会导致其微分方程系数不断发生变化，通过建立换流器及换流变压器的状态空间模型，利用关联矩阵包含了所有工况，在求解过程中通过更新阀电阻阻值进入不同工况，从而调用对应的微分方程进行求解，实现了将处于不同工况下的换流器及换流变压器模型表示成统一的矩阵形式。

通过算例与分析可知，本文模型与PSCAD的仿真结果基本一致，证明了所提算法的有效性和正确性。

附录

换流变压器和换流器的数学模型中式(5)的各参数矩阵分别为

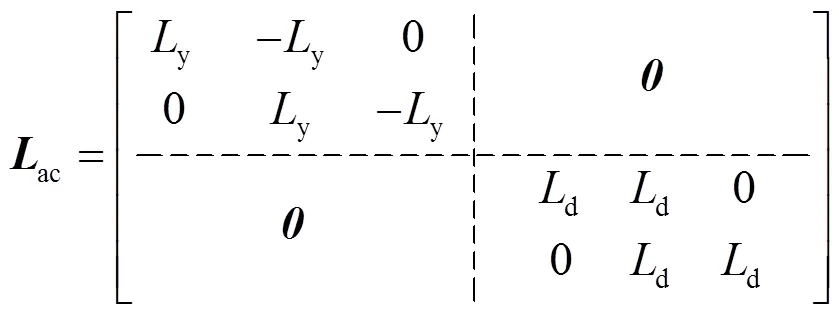
直流线路模型中式(17)的各参数矩阵为

直流线路模型式(18)中详细参数矩阵为

生成主设备系统状态空间模型中式(19)各参数矩阵为

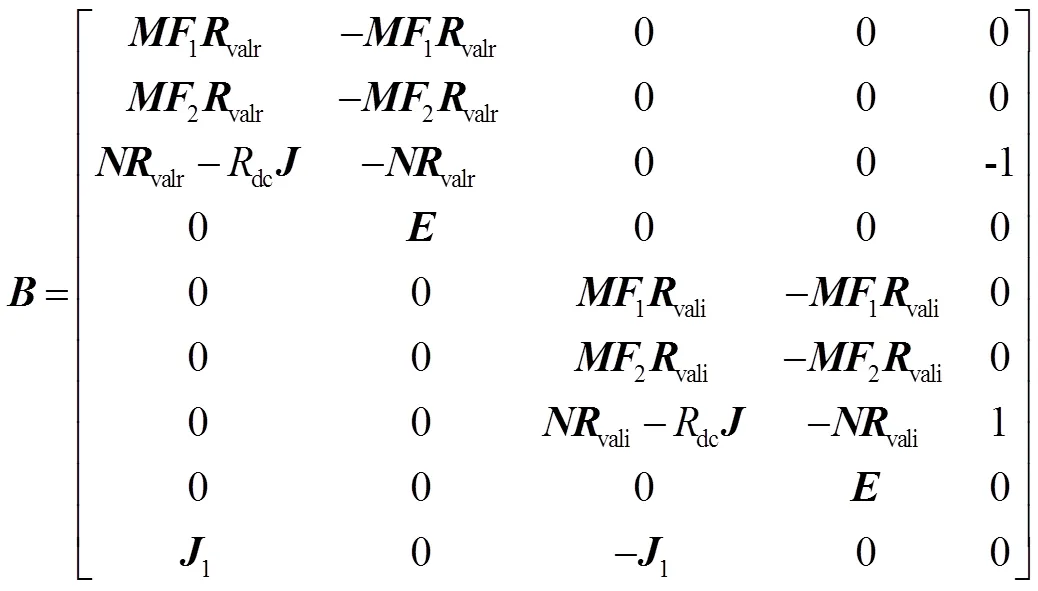
[1] 熊华强, 杨程祥, 马亮, 等. 含分层接入特高压直流的交直流混联电网机电—电磁暂态混合仿真研究[J]. 电力系统保护与控制, 2020, 48(24): 145-153.

XIONG Huaqiang, YANG Chengxiang, MA Liang, et al. Electromechanical-electromagnetic transient hybrid simulation of an AC/DC hybrid power grid with UHVDC hierarchical connection mode[J]. Power System Protection and Control, 2020, 48(24): 145-153.

[2] 李高望, 陈锐智, 陈艳波. 考虑网络划分优化的交直流系统并行电磁暂态仿真研究[J]. 电力系统保护与控制, 2021, 49(4): 72-80.

LI Gaowang, CHEN Ruizhi, CHEN Yanbo. Research on parallel electromagnetic transient simulation of an AC-DC system considering optimization of network division[J]. Power System Protection and Control, 2021, 49(4): 72-80.

[3] 祝佳佩, 赵文彬. 考虑线路潮流波动对母线电压影响的特高压交流电网电压控制策略[J]. 电力系统保护与控制, 2021, 49(6): 76-82.

ZHU Jiapei, ZHAO Wenbin. Voltage control strategy of a UHV AC power grid considering the influence of line power flow fluctuation on bus voltage[J]. Power System Protection and Control, 2021, 49(6): 76-82.

[4] 郭琦. 交直流混联电网运行控制实时仿真技术研究[J].南方电网技术, 2017, 11(3): 59-64.

GUO Qi. Research on real-time simulation technology of operation control of AC & DC hybrid power system[J]. China Southern Power System Technology, 2017, 11(3): 59-64.

[5] 毛晓明, 管霖, 张尧, 等. 含有多馈入直流的交直流混合电网高压直流建模研究[J]. 中国电机工程学报, 2004, 24(9): 72-77.

MAO Xiaoming, GUAN Lin, ZHANG Yao, et al. Researches on HVDC modeling for AC/DC hybrid grid with multi-infeed HVDC[J]. Proceedings of the CSEE, 2004, 24(9): 72-77.

[6] 戚庆茹, 焦连伟, 严正, 等. 高压直流输电动态相量建模与仿真[J]. 中国电机工程学报, 2003, 23(12): 31-35.

QI Qingru, JIAO Lianwei, YAN Zheng, et al. Modeling and simulation of HVDC with dynamic phasors[J]. Proceedings of the CSEE, 2003, 23(12): 31-35.

[7] VEGA-HERRERA J, RAHMANN C A, VALENCIA F, et al. Analysis and application of quasi-static and dynamic phasor calculus for stability assessment of integrated power electric and electronic systems[J]. IEEE Transactions on Power Systems, 2021, 36(3): 1750-1760.

[8] SHU D, XIE X, DINAVAHI V, et al. Dynamic phasor based interface model for EMT and transient stability hybrid simulations[J]. IEEE Transactions on Power Systems, 2018, 33(4): 3930-3939.

[9] 岳程燕, 田芳, 周孝信, 等. 电力系统电磁暂态-机电暂态混合仿真接口原理[J]. 电网技术, 2006, 30(1): 23-27, 88.

YUE Chengyan, TIAN Fang, ZHOU Xiaoxin, et al. Principle of interfaces for hybrid simulation of power system electromagnetic-electromechanical transient process[J]. Power System Technology, 2006, 30(1): 23-27, 88.

[10] XU W, QIANG S. Research on electromechanical transient-electromagnetic transient hybrid simulation algorithm for power system[C] // International Conference on Information Systems and Computer Aided Education (ICISCAE), July 6-8, 2018, Changchun, China.

[11] KWON D, KIM Y, MOON S. Modeling and analysis of an LCC HVDC System using DC voltage control to improve transient response and short-term power transfer capability[J]. IEEE Transactions on Power Delivery, 2018, 33(4): 1922-1933.

[12] LIU H, SUN J. Modeling and analysis of DC-link harmonic instability in LCC HVDC systems[C] // IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), June 23-26, 2013, Salt Lake City, UT, USA.

[13] HWANG M S, WOOD A R. Harmonic state-space modelling of a controlled HVDC converter[J]. Electric Power Systems Research, 2015, 124: 65-73.

[14] 李崇涛, 林啸, 赵勇, 等. 高压直流输电系统暂态过程的解析解法(一): 数学模型[J]. 电网技术, 2017, 41(1): 1-8.

LI Chongtao, LIN Xiao, ZHAO Yong, et al. An analytical solution for transient process of HVDC transmission system part 1-mathematical model[J]. Power System Technology, 2017, 41(1): 1-8.

[15] 李崇涛, 林啸, 赵勇, 等. 高压直流输电系统暂态过程的解析解法(二): 算法与算例[J]. 电网技术, 2017, 41(1): 8-13.

LI Chongtao, LIN Xiao, ZHAO Yong, et al. An analytical solution for transient process of HVDC transmission system part 2-algorithm and example[J]. Power System Technology, 2017, 41(1): 8-13.

[16] 程佩芬, 李崇涛, 傅闯, 等. 基于状态空间法的高压直流输电系统电磁暂态简化模型的解析算法[J]. 电工技术学报, 2019, 34(6): 1230-1239.

CHENG Peifen, LI Chongtao, FU Chuang, et al. An analytic solution for simplified electromagnetic transient model of HVDC transmission system based on state space method[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1230-1239.

[17] 鲁成栋, 肖登明, 秦松林. 特高压直流换流阀的运行性能及其失效机制[J]. 电气技术, 2014(4): 5-10.

LU Chengdong, XIAO Dengming, QIN Songlin. Study on operating performance and failures mechanism of UHVDC thyristor valves[J]. Electrical Engineering, 2014(4): 5-10.

[18] 昆德. 电力系统稳定与控制[M]. 周孝信, 宋永华, 李兴源, 等译. 北京: 中国电力出版社, 2002.

[19] 尉龙, 宋吉江, 孙磊. 基于PSCAD的CIGRE HVDC模型控制系统研究[J]. 山东理工大学学报(自然科学版), 2014, 28(5): 69-75.

WEI Long, SONG Jijiang, SUN Lei. The research on the control system of CIGRE HVDC model based on PSCAD[J]. Journal of Shandong University of Technology (Nature Science Edition), 2014, 28(5): 69-75.

[20] FARUQUE M O, ZHANG Y Y, DINAVAHI V. Detailed modeling of CIGRE HVDC benchmark system using PSCAD/EMTDC and PSB/SIMULINK[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 378-387.

[21] ATIGHECHI H, CHINIFOROOSH S, JATSKEVICH J, et al. Dynamic average-value modeling of CIGRE HVDC benchmark system[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2046-2054.

[22] 王璐, 李凤婷, 尹纯亚, 等. 考虑直流电流变化的HVDC系统不对称故障换相失败分析[J]. 电力系统保护与控制, 2021, 49(1): 17-23.

WANG Lu, LI Fengting, YIN Chunya, et al. Analysis of asymmetric fault commutation failure in an HVDC system with DC current variation[J]. Power System Protection and Control, 2021, 49(1): 17-23.

State-space model and solution algorithm of an HVDC system considering a snubber circuit

LI Zhixian1, LI Huan2, LIU Chongru1, ZHENG Le1, WEI Wei2, YU Jianyu1

(1. State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China; 2. State Key Laboratory of HVDC, Electric Power Research Institute (China Southern Power Grid), Guangzhou 510663, China)

To improve the accuracy of the simulation calculation of an HVDC transmission system based on state-space method, a method for an HVDC system considering a snubber circuit is proposed. Valve current and snubber current are used as state variables to model a thyristor. The voltage transformation relation of a converter transformer under different working conditions is expressed as a unified form by a correlation matrix, so as to establish the state-space model of converter and converter transformer, from which the state-space expression of primary equipment in an HVDC system is derived simultaneously with the DC line model. Also, a calculation method of trigger angle in the control system is proposed. A data interaction process between the primary equipment system and the control side system is introduced. As a result, a high-precision solution of the mathematical model of an HVDC system is realized. Finally, algorithm results realized by Matlab are compared with the simulation results of PSCAD, and the solving accuracy of the primary system can reach 99.99%.

HVDC transmission system; state-space method; snubber loop; snubber current; electromagnetic transient simulation

10.19783/j.cnki.pspc.211025

南方电网科技项目资助(ZBKJXM20180104)

This work is supported by the Science and Technology Project of Southern China Power Grid (No. ZBKJXM20180104).

2021-08-04；

2021-10-09

李志显(1997—)，男，硕士，研究方向为高压直流输电暂态仿真计算；E-mail：lizhixian777@163.com

刘崇茹(1977—)，女，通信作者，博士，教授，主要研究方向为交直流混合系统分析、仿真、运行与控制。E-mail: chongru.liu@ncepu.edu.cn

(编辑 周金梅)