基于时域融合Transformers的可解释预测模型及其应用研究

陈孝文,苏 攀,李夏青,张 俊,王 林

(1.湖北中烟工业有限责任公司，湖北 武汉 430040；2.湖北省社会科学院经济研究所，湖北 武汉 430077；3.华中科技大学 管理学院，湖北 武汉 430074)

随着大数据时代的到来，当前的预测研究能够在复杂的决策情境下，结合大量数据学习构建分析系统，对真实世界数据的分布做出模拟。预测问题无处不在，如产品供给需求预测、粮食霉变预测、电力产能预测、舆论周期预测等。然而，由于预测需求的多样化，传统的数据处理方法已经很难满足要求。因此，需要提出精度更准、数据处理效率更高、泛化能力更强的预测方法。

关于预测模型，已有学者做出大量研究并应用于各类领域。WANG等[1]结合经验模型分解和人工智能模型对风速进行预测，得出混合模型能提高预测精度的结论。FAN等[2]提出了一种用于多视距时间序列预测的端到端深度学习预测模型，并在两个不同领域的大规模预测数据集上证明了该模型的有效性。LI等[3]提出用变换器来解决时间序列预测问题。LUNDBERG等[4]提出了一个解释预测模型SHAP，其能为每个特征分配一个特定预测的重要值。RIBEIRO等[5]将新的解释技术LIME加入到解释模型中，通过解释文本和图像分类等不同模型验证了方法的灵活性。冉靖等[6]对ARIMA等概率统计模型、支持向量机等机器学习模型、深度学习模型、模型分解方法等基本预测方法和组合预测方法进行对比分析，总结了各类方法的优点和局限性。张莉等[7]利用改进的GARCH-MIDAS模型提高了股票波动率的预测性能。李洁等[8]构建了基于长短时记忆网络(LSTM)的高速铁路客流预测模型，证明了LSTM 客流模型比其他模型预精度更高。杨青等[9]基于深度神经网络优化技术构造了一个深层LSTM神经网络，并将其应用于全球30个股票指数3种不同期限的预测研究。郭金录[10]提出了融合变分模态分解(VMD)、集合经验模态分解二层分解技术及长短期记忆深度神经网络的沪深300股指收益率组合预测模型。崔焕影等[11]基于经验模态分解算法(EMD)、遗传算法(GA)、神经网络(BP)等模型及其组合预测模型，对中国碳市场交易价格进行短期预测和长期预测。

目前，已有模型大多数是“黑盒”模型，即由各参数之间复杂的非线性交互来产生预测结果。此类模型的问题在于难以解释模型的预测过程，无法判断模型求解结果的可靠性。而常用的深度神经网络(DNN)解释方法又不适用于时间序列，后置方法也没有考虑输入特征的时间或延迟。在时间序列中时间步之间的相关性通常较为显著，所以后置方法会降低解释的质量。也有学者提出了一种基于注意力的预测模型，可以用来解释时序数据。不同于其他模型，多视界预测包含许多不同类型的输入特征，可为多视界预测提供相关的时间步，但不能在给定的时间步中标注不同特征的重要性。因此，需要新方法来解决多维水平预测中数据的异构性，并使这些预测具有可解释性。

综上，笔者提出了一种结合变分模态分解 (variational mode decomposition,VMD)和时域融合变换器(temporal fusion transformer,TFT)的预测模型，VMD用于充分挖掘原始数据特征，TFT模型能在保证高性能预测的同时为预测过程提供一定的解释。最后，以白卡纸价格数据为例，验证所提模型的可行性，并给出可解释性的预测过程。

1 基于时域融合Transformers的可解释预测模型

变分模态分解是一种自适应、完全非递归的模态变分和信号处理的方法，可以根据实际情况确定所给序列的模态分解个数，通过匹配每种模态的最佳中心频率和有限带宽，实现固有模态分量(IMF)的有效分离和信号的频域划分，得到给定信号的有效分解成分，最终获得变分问题的最优解。时域融合变换器 是一种基于注意力的多视界预测深度学习神经模型，结合了高性能的多元预测与时态动力学的可解释洞察。TFT使用递归层进行局部处理，使用可解释的自我注意层进行长期依赖，从而学习不同尺度下的时间关系。TFT利用特定的组件来选择相关的特征，并利用一系列的门控层来抑制不必要的特征，从而在各个场景中均保持较高性能。

1.1 变分模态分解

VMD是DRAGOMIRETSKIY和ZOSSO[12]于2014年提出的一个完全非递归的模型，可捕获原始数据的不规则特征，是一种有效的信号分解方法，比经验模态分解(EMD)具有更好的适应性和分解效果。在VMD中，原信号f(t)被VMD分解成多个子模态uk,k=1,2,…,K，每个子模态都有一个中心频率ωk。VMD的目标函数是使各子模态的频带宽度之和最小，约束条件为各子模态的频带宽度之和等于原始信号。

(1)

式中：j为虚数单位；t为迭代次数；K为子模态数；δ(t)为Dirac分布；*为卷积。

然后，通过引入二次惩罚项alpha和拉格朗日乘子λ(t)，将约束问题转化为无约束问题，从而得出上述问题的最优解。alpha可以保证在高斯噪声存在的情况下精确地重构子模态，λ(t)可以保证无约束问题等价于有约束问题。其中，无约束问题可以描述为：

(2)

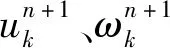
(3)

(4)

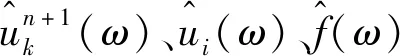
(5)

(6)

式中：τ为更新后的参数；ε为计算精度。

(7)

式中：f(t)为原始信号序列；uk(t)为分解后的子模态；K为子模态数；Ns为样本个数。根据以往经验，当rres没有明显下降趋势时，模态数即可确定。

1.2 时域融合变换器

时域融合变换器是谷歌云人工智能团队提出的一种内在可解释的多视界的时间序列预测深度学习模型，比一般黑盒模型具有更强的解释能力。多水平预测问题通常包含复杂的输入，包括静态协变量、已知的未来输入和其他只有在历史上观察到的外生时间序列，而TFT将高性能的多水平预测与可解释的见解相结合。利用静态协变量编码器来编码上下文向量；利用门控机制和依赖于样本的变量选择，最大程度地减少无关输入；序列到序列层，用于本地处理已知和观察到的输入；时间自注意解码器，用于了解数据集中存在的任何长期依存关系。TFT的模型架构如图1所示。TFT能够高效使用规范组件为每种输入类型构建特征表示，从而提高各种预测问题的预测性能。

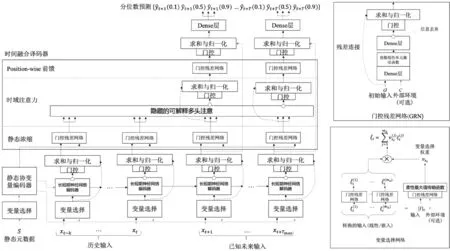
图1 时域融合变换器的模型结构

TFT包括5个主要组成部分，即门控机制、变量选择网络、静态协变量编码器、时间处理和多水平预测区间预测。①门控机制，它的功能是跳过架构中所有未使用的组件，提供自适应深度和网络复杂性，以适应不同的数据集和场景。②变量选择网络，在每个时间步长选择相应的输入变量。③静态协变量编码器，将静态特征集成到网络中，通过编码上下文向量来约束时间动态。④时间处理，从观察值或已知时变输入中学习长期或短期的时间关系。序列到序列层用于本地处理，而长期项取决于一个新的可解释的多头注意块捕获的使用。⑤多水平预测区间预测，通过分位数预测来确定每个预测区间内可能的目标值的范围。

1.2.1 控制机制

门控残差网络(GRN)能够使模型的变量与目标之间的非线性运算更加灵活。GRN包含主输入a和可选上下文c两种类型的输入。

GRNω(a,c)=LayerNorm(a+GLUω(η1))

(8)

η1=W1,ωη2+b1,ω

(9)

η2=ELU(W2,ωa+W3,ωc+b2,ω)

(10)

式中：ELU为指数线性单元激活函数；η1和η2为中间层，η1、η2∈Rdmodel；dmodel为隐藏状态大小；LayerNorm表示标准层归一化；ω为权重共享；W(.)为权重，W(.)∈Rdmodel×dmodel。

基于门控线性单元(GLUs)的组件门控层可以提供弹性，以抑制给定数据集不需要的任何体系结构。

GLUω(γ)=σ(W4,ωγ+b4,ω)⊙(W5,ωγ+b5,ω)

(11)

式中：γ为输入参数,γ∈Rdmodel；σ(.)为sigmoid激活函数；b(.)为偏差,b(.)∈Rdmodel；⊙为元素Hadamard的乘积。GLU允许TFT控制GRN对初始输入的贡献度。

1.2.2 变量选择网络

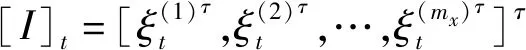
Vxt=Softmax(GRNVx([I]t,cs))

(12)

(13)

(14)

1.2.3 可解释的多头注意力

TFT采用自注意机制学习不同时间步长之间的长期关系，该机制对基于变换器的多头注意结构进行了改进，增强了可解释性。一般来说，基于Q∈RN×dattn与键K∈RN×dattn之间的关系，注意机制将V∈RN×dV的值标度如下:

Attention(Q,K,V)=A(Q,K)V

(15)

式中：N为输入注意层的时间步长；A()为归一化函数。针对注意力值，尺度点积通常采用如下方法:

(16)

注意机制的学习能力采用多头注意方法，对不同的表示子空间采用不同的注意头:

MultiHead(Q,K,V)=[H1,H2,…,HmH]WH

(17)

(18)

考虑到每个头使用不同的值，单一注意力权重不能表明特定特征的重要性。因此，将多头注意力修改为每个头的共享值，并对所有头进行相加聚合:

(19)

(20)

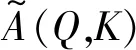
1.2.4 分位数输出和损失函数

TFT通过同时预测每个时间步的不同百分位数(如10、50和90)来生成点预测区间。分位数预测则是利用时域融合解码器的线性变换输出产生。采用联合最小化分位数损失来训练TFT，并将所有分位数的输出相加，具体方法如下:

(21)

(22)

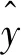
2 模型应用分析

白卡纸是由纯优质木浆制成的白色卡纸，主要用于包装装潢用的印刷承印物，有较高的挺度、耐破度和平滑度。白卡纸作为产品包装纸和塑料的主要替代品，随着食品、3C产品、化妆品销量的逐年增长，以及 2021年1月1日“禁塑令”的推出，白卡纸的价格经历了快速拉升，又急速下跌的“火与冰”的行情。准确预测白卡纸价格不仅具有重要的现实意义，也具有较高的挑战性。因此，笔者以白卡纸价格为例，进行VMD-TFT可解释预测模型的应用研究。

2.1 数据来源

白卡纸价格数据来源于《造纸信息》期刊(http://zzxx.ijournals.cn/)每月发布的各品牌白卡纸的均价。其中，2010年1月到2020年12月的白卡纸价格数据为训练集，2021年1月到2021年9月的白卡纸价格数据为测试集。2010年1月—2021年9月白卡纸价格如图2所示，可以看出受原材料纸浆价格上涨的影响，自2020年9月白卡纸价格节节攀登，至2021年5月白卡纸价格才开始回落。

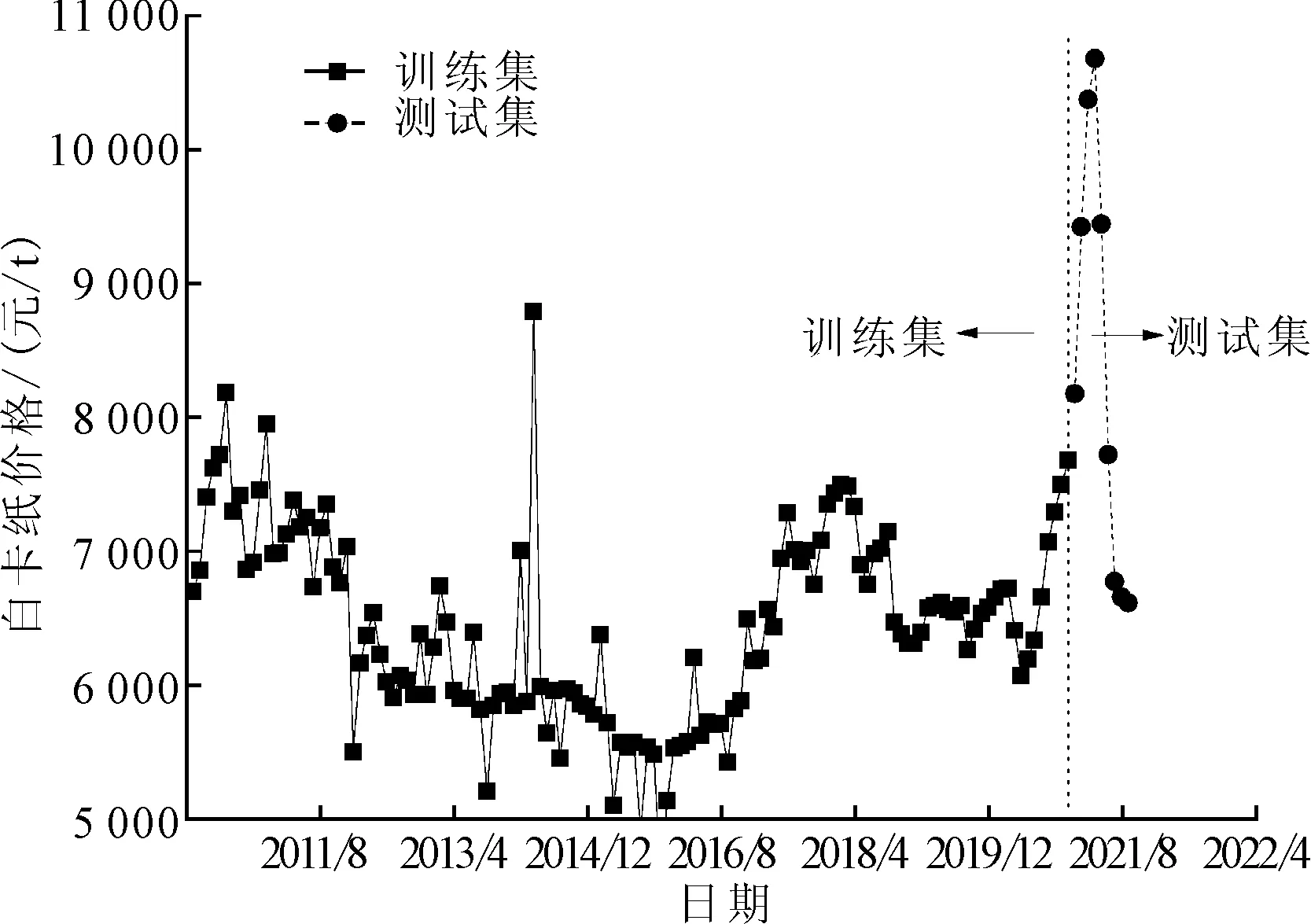
图2 2010年1月—2021年9月白卡纸价格

2.2 预测性能评估指标

运用均方误差(RMSE)、平均绝对百分比误差(MAPE)和平均绝对误差(MAE)3个指标计算测试集的精度：

(23)

(24)

(25)

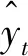
2.3 预测结果与讨论

(1)单因素预测。使用向量自回归(VAR)模型来选择每月白卡纸价格预测合适的滞后阶数。VAR模型选择滞后阶数采用4个推荐指标:赤池信息量准则(Akaike information criterion，AIC)、贝叶斯信息准则(Bayesian information criterion，BIC)、最终预报误差准则(final prediction error，FPE)和Hannan-Quinn信息准则(HQIC)。VAR 模型的结果如表1所示，AIC、FPE、HQIC皆推荐12为滞后阶数，即用滞后12个月的白卡纸价格来预测当月的白卡纸价格最合适。采用网格搜索法来寻找模型最优的参数组合，通过多次实验，设置时域融合TFT模型的参数为：学习速率为0.3，注意头的数量为1，隐藏层数为16，隐藏连续数为8，每次迭代数据集大小为32。单因素TFT的预测结果显示MAPE为18.02%，预测效果较差。为应对单因素模型预测性能低的问题，笔者考虑使用VMD分解模型对原始序列进行分解，以更充分地提取数据的特征。

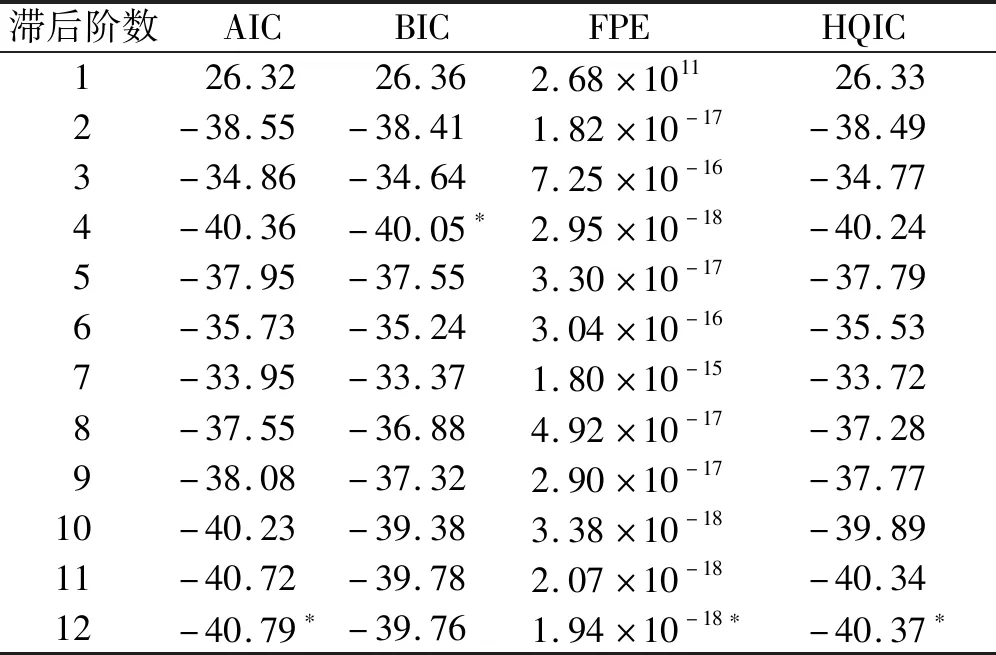
表1 白卡纸价格滞后阶数的选择

(2)VMD-TFT多因素可解释预测模型。为了减少白卡纸价格序列的非平稳特性，采用VMD方法将原始价格序列分解为多个子模态。经过数次实验后，将分解的子模态数目定为4，分解后的子序列能取得较好的预测效果。分解后的子序列如图3所示，低频子模态代表了原始白卡纸价格序列的总体趋势，高频子模态则反映了局部的波动趋势，能很好地反映价格波动的拐点。经过VMD提取后的子序列比原数据更加平滑，有利于提高白卡纸价格预测的性能。

图3 2010年1月—2021年9月白卡纸价格原序列及VMD分解后的子序列

为验证所提出的时域融合TFT模型的预测效果，选用流行的BP神经网络(BPNN)、支持向量机(SVM)、循环神经网络(RNN)、长短期神经网络(LSTM)和门控循环神经网络(GRU)作为对比算法。与单因素模型滞后12个月保持一致，多因素预测的滞后阶数也选择12个月。所有模型均通过Python软件进行编码。经过多组实验，时域融合TFT模型的参数设置为：学习速率为0.3，注意头的数量为1，隐藏层数为8，隐藏层神经元个数为4，每次迭代数据集大小为32。BPNN、SVM、RNN、LSTM和GRU的参数设置如表2所示。

表2 各预测模型的参数设置

各模型的预测结果如表3所示，对比MAPE、RMSE、MAE3个性能指标可以看出，VMD-TFT模型的预测精度比BPNN、SVM、RNN、LSTM、GRU及单因素TFT均有明显的提升，且VMD-TFT较其他模型能取得更贴近真实值的预测值(如图4所示)，能够达到满意的预测性能。通过与单因素预测的结果对比可以发现，使用VMD分解后的预测模型比仅使用历史价格序列预测的MAPE值更低，证明其预测性能更加优异。

表3 预测结果展示与对比

图4 各模型预测值与真实值对比图(2021年1月—2021年9月)

TFT模型的输入变量可解释性权重如图5所示，可知序列S2、S3对于白卡纸价格预测的贡献更大，S1和S4的贡献较低。这是因为S1反映的是白卡纸价格波动的大致趋势，S4反映的是分解后的残差，故其对预测的贡献较低。

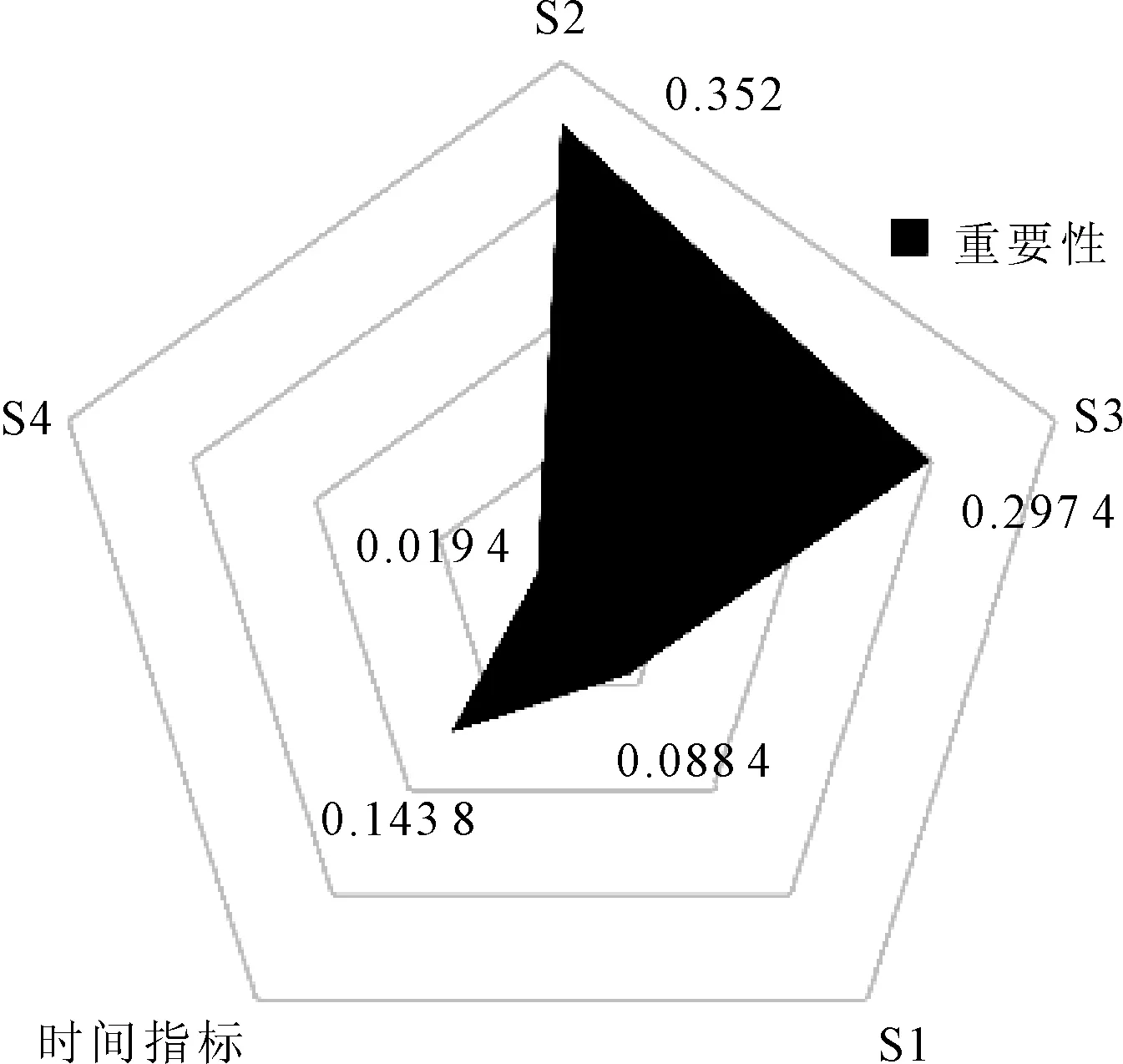
图5 各输入变量可解释性权重

3 结论

笔者重点研究了变分模态分解和时域融合变换器相结合的高效可解释预测模型，VMD有助于充分提取复杂数据中隐藏的特征，TFT模型具备高效的预测性能，且能给出可解释性的预测过程。同时，构建一个高效的白卡纸价格预测框架，可有效应对近年来白卡纸价格波动剧烈的挑战，为可解释预测的研究提供了新的应用。

在新冠肺炎疫情和国际经济政策局势不动变化的背景下，如白卡纸等大宗商品的价格预测非常复杂，未来可以考虑更多的输入因素，如国际经济情况和白卡纸销量等影响。同时，TFT模型具备很强的解释能力，本研究只用了深度学习模型的部分结构，未来可以考虑更多因素来挖掘TFT模型的潜能，如过去已知变量、未来已知变量等，从而进一步提高预测精度。