滇西南巨尾桉人工林林木根径与胸径的相关关系研究

高德祥，韦文长

(1. 云南省林业调查规划院，云南 昆明 650051； 2. 双江县林业和草原局，云南 双江 677399)

巨尾桉(Eucalyptusgrandis×E.urophylla)是以巨桉(EucalyptusgrandisHill ex Maiden)为母本、尾叶桉(EucalyptusurophyllaS. T. Blake)为父本培育而成的杂交种，继承了母本干形通直，萌芽能力强以及父本速生丰产的优良性状，是经营短周期工业原料林、生产优质木材和纸浆用材的优良树种，具有生长快、轮伐期短、技术成熟、病虫害少以及经济效益好的优点[1]，是我国南方短周期工业原料林的主要造林树种之一[2]。双江县自2009年引进巨尾桉以来，累计种植面积已达6 000 hm2，目前已全面进入收获期，为胶合板加工和造纸行业提供了大量的原材料。

随着巨尾桉产业的大规模发展，盗伐、滥伐林木案件以及林权纠纷时有发生，特别是在近几年的森林督查工作中也出现了一些违法采伐巨尾桉人工林的图斑。对于这类性质的图斑地块，由于伐倒木已被运出伐区，在地上仅存伐桩而又缺乏根径材积表的情况下，如何通过根径精确地估测林木材积[3]是林业主管部门和执法部门面临的一项技术问题。林业执法机关在处理这类案件工作中，大多数倾向于采用胸径材积表法，即在相近林分中测量一定数量立木的根径和胸径, 用回归方法求出涉案林木根径对应的胸径，再查胸径材积表测算出涉案材积[4-7]。

在根径与胸径相关关系的研究方面，曾慎松开展了巨尾桉人工林根径与胸径模型研究，确定对数方程是巨尾桉人工林根径与胸径相关关系的最佳模型[8]；王韦舒开展了辽宁丹东落叶松(Larixgmelinii(Ruprecht) Kuzeneva)根径与胸径的相关性研究，确定三项式曲线方程拟合效果最佳[9]；闭海秀等开展了桂东区杉木(Cunninghamialanceolata(Lamb.) Hook.)地径与胸径的相关分析，认为线性方程是杉木地径与胸径相关关系的最佳模型[10]；李辉开展了马尾松(PinusmassonianaLamb.)地径与胸径关系模型的比选研究，认为幂函数方程是马尾松根径与胸径相关关系的最佳模型[11]。综上所述，国内在对根径与胸径相关性研究的方法方面均采用了模型优选法，根据评价指标选择最优的根径-胸径数学模型，区别之处是不同地区的不同树种其最佳根径-胸径数学模型也不同。

根径与胸径是林业测树中的两项重要因子，其内在关系直接反映了树干下部干形的变化趋势[12]。根径与胸径的相关关系在不同的树种之间以及不同立地条件之间差异性显著，同一树种在一定区域内也有一定规律，确定两者的关系在林业生产实际中有着重要作用[13]。为解决根径一元材积表存在不足的问题，满足林业生产经营和森林资源管理工作的需要，在对研究样木数据进行野外采集、整理、分析的基础上，重新编制了根径-胸径对应表以满足以根径位置采伐方式事后采伐量核定的需要[14]。

1 研究区概况

研究区双江县位于云南省西南部，地理坐标为东经99°35′15″～100°09′33″，北纬23°11′58″～23°48′50″，国土总面积2 157.10 km2。县境东部与景谷县隔江相望，南与澜沧、沧源两县毗邻，西与耿马县相依，北与临翔区接壤，澜沧江、小黑江为双江县与景谷、澜沧和沧源三县接壤之界河。全县总体属中山地貌，地势西北高而东南低，最高海拔3 233 m，最低海拔670 m；境内河流属澜沧江水系，长度在1 km以上的溪河有106条，水资源丰富；北回归线横穿县境中部，在水平气候带上属低纬度南亚热带山地季风气候，历年平均日照时间为2 223.3 h，全年≥10 ℃的积温7 126.3 ℃，年均温19.5 ℃，平均无霜期355 d，年均降雨量1 100 mm，平均相对湿度76%，干湿季分明，立体气候明显；境内分布的地带性土壤有砖红壤、赤红壤、红壤、黄壤、黄棕壤、棕壤、亚高山灌丛草甸土7个土类。优越的自然条件为建设森林生态、发展林业产业奠定了坚实的营林立地条件基础。据最新森林资源监测数据，全县森林覆盖率为70.73%，活立木蓄积量为1 135万m3。

2 材料与方法

2.1 材料的收集与处理

根据双江县境内巨尾桉人工林的分布状况，按照《林业数表编制数据采集技术规程》[15]对样本数量的相关要求，在不同立地条件、不同经营水平的3个巨尾桉人工林伐区，在6～22 cm胸径径阶区间随机选取树干通直圆满、无分杈的巨尾桉样木138株，其中：编表样本103株，检验样本35株，各径阶样木较均匀分布。收集样木的伐区涵盖坝区、半山区和高海拔山区，样木来源于不同的坡位、坡向、坡度和土壤，样木的选择具有较广泛的代表性。138株样木按径阶分布及树高幅度统计详见表1。

材料的处理与编制巨尾桉一元、二元立木材积表的研究课题一致，即在统一伐根高度为10 cm条件下将样木伐倒后，以2 m(树高10 m以上)或1 m(树高10 m以下)区分段造材，量测并记录伐桩、胸径、各区分段中央直径、梢头底径和长度，采用中央断面积区分求积法计算各区分段材积，采用圆锥体公式计算梢头材积。各区分段材积与梢头材积的总和即为样木的单株木总材积。根据本文研究目的，选取有实际应用价值的样木根径和胸径值作为研究数据。

表1 样木按径阶分布及树高幅度统计Tab.1 Statistics of sample wood distribution according to diameter rank and tree height range

2.2 根径-胸径数学模型的选择

根据103株编表样本的根径、胸径实测值 ，以根径为横坐标，胸径为纵坐标绘制散点(图1)。

由图1可见，根径-胸径散点图中点的分布总体上呈现线形，为准确估计两个变量之间的关系，选择包括线性方程、对数函数、二次方程、三次方程、幂函数的5个数学模型作为备选模型，经拟合方程参数并充分比较各项评价指标，选出拟合效果最佳的方程作为巨尾桉根径-胸径数学模型。备选的根径-胸径数学模型见表2。

2.3 根径-胸径数学模型的拟合与评价

将103株编表样本的造材样木数据代入表2中的数学表达式，使用SPSS软件回归分析曲线估计方法对各模型进行拟合并求解参数，以离差平方和(SSR)、相关指数(R2)、总相对误差(RS)、相对误差平均值(REA)、相对误差绝对值平均值(REAA)和残差(SR)分布图作为评价指标[16]。各评价指标计算公式为：

图1 巨尾桉根径-胸径关系散点图Fig.1 Scatter diagram of root diameter-diameter breast height relationship of Eucalyptus grandis×E.urophylla

表2 备选根径-胸径数学模型Tab.2 Alternative mathematical models of root diameter-diameter breast height

式中：D为胸径(cm)；DR为根径(cm)；a0、a1、a2、a3为方程参数。

(1)

(2)

(3)

(4)

(5)

SR=Di-D＾i

(6)

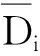
2.4 最优模型的确定

根据备选模型的拟合结果，综合各项评价指标，选择离差平方和(SSR)小、相关指数(R2)大、总相对误差(RS)小、相对误差平均值(REA)小、相对误差绝对值平均值(REAA)小、残差图以横轴为中心分布均匀的模型作为最优的巨尾桉根径-胸径数学模型。

2.5 根径-胸径数学模型的适用性检验

利用实测数据中随机抽取的35株未用于建模的数据对优选的根径-胸径数学模型进行适用性检验，检验指标包括检验样本胸径实际值与估计值之间的总相对误差(RS)、相对误差绝对值平均值(REAA)、残差分析和F检验结果。总相对误差(RS)在±5%范围内、相对误差绝对值平均值(REAA)小于10%、残差图以横轴为中心分布均匀并通过F检验(F≤F0.05)时，认为此根径-胸径数学模型适用。

3 结果与分析

3.1 备选根径-胸径数学模型的拟合评价

使用103株编表样本数据对备选的5个根径-胸径数学模型进行拟合并求解参数，计算出各模型的评价指标下(表3)。

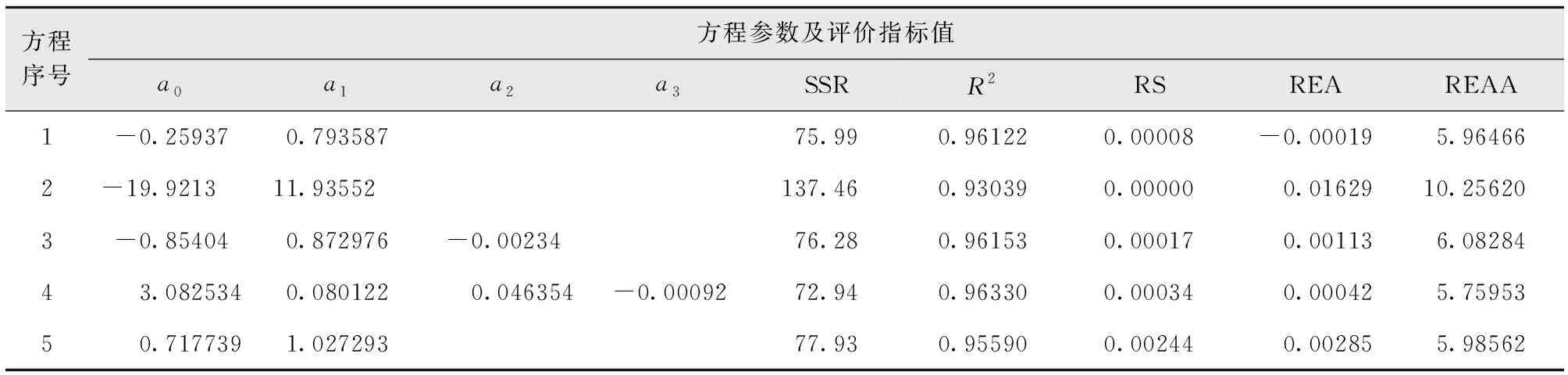
表3 备选根径-胸径数学模型参数及评价指标值Tab.3 Statistics of parameters and evaluation values of alternative root diameter-diameter breast height model

由表3可以看出，5个备选模型拟合效果良好。除2号模型外，其他4个模型的相关指数(R2)均在95%以上，相对误差绝对值平均值(REAA)均在6%上下，具有很高的拟合精度。

以根径为横轴，胸径残差为纵轴，绘制1、3、4、5号模型的胸径残差分布图(图2～图5)。

3.2 最优根径-胸径数学模型的确定

根据各方程的离差平方和(SSR)、相关指数(R2)、总相对误差(RS)、相对误差平均值(REA)和相对误差绝对值平均值(REAA)这几项评价指标的综合得分评价结果，对备选根径-胸径数学模型的各项评价指标值进行比较排序，1号模型和4号模型拟合精度最高，综合误差最小，总得分排序最高，各模型综合得分及排序见表4。

由表4可以看出，5个备选模型综合得分由高到低排序为：4号模型>1号模型>3号模型>5号模型>2号模型。

从胸径残差分布图(图2～图5)可见， 4号模型的散点更密集、更均匀地分布在残差值为0的中轴线上。综合以上评价，认为4号模型D=a0+a1×DR+a2×DR2+a3×DR3是5个备选巨尾桉根径-胸径数学模型中最优的数学模型。

图2 1号模型胸径残差分布Fig.2 Residual distribution of DBH in Model 1

图3 3号模型胸径残差分布Fig.3 Residual distribution of DBH in Model 3

图4 4号模型胸径残差分布Fig.4 Residual distribution of DBH in Model 4

图5 5号模型胸径残差分布Fig.5 Residual distribution of DBH in Model 5

表4 备选根径-胸径回归方程综合得分及排序Tab.4 Comprehensive score and ranking of alternative root diameter-diameter breast height regression equation

3.3 根径-胸径数学模型的适用性检验

3.3.1误差和残差检验

使用35株检验样本数据对4号模型进行适用性检验，结果显示：总相对误差(RS)为1.435%，在±5%的误差范围内；相对误差绝对值平均值(REAA)为5.93211%，小于10%的误差范围。残差分析结果显示，残差图以横轴为中心分布均匀(图6)。

3.3.2F检验

检验样本胸径实际值(Li)的计算公式为：

Li=a+b×L＾i

在词频表达式中，Ft为某一词汇t的频率强度；Rt是词汇t的频度，即词汇t在文本统计中出现的次数；Lt是文本统计中词汇t的字数长度；L文本统计中所有的字数长度。依照此公式计算，按照频率由高到低选取与黄山民宿有关的20个高频词汇，如表1所示。

(7)

式中：L＾i为检验样本胸径估计值；a、b为估计参数。

使用SPSS软件回归分析曲线估计法对方程进行拟合，参数估计值为：a=-0.351 233，b=1.042 808。检验统计量(F)计算公式为：

(8)

将方程参数a、b值、样本数量m值及检验样木35株样木胸径实际值和估计值统计数据代入公式(8)，计算得F值为1.08，小于F0.05(1,33)的查表值4.14，确定的最优数学模型通过F检验。

综合以上检验结果表明，4号模型适合作为巨尾桉根径-胸径数学模型，代入表3中的参数值后，最优根径-胸径数学模型公式为：

D=3.082534 + 0.080122DR + 0.046354DR2-

0.000920DR3

(9)

图6 最优根径-胸径数学模型检验样本胸径残差分布Fig.6 Test sample residuals of the optimal root diameter-diameter breast height model

3.4 根径-胸径对照表的展开

《云南省森林资源规划设计调查操作细则》[17]规定的林木检尺起测胸径为5 cm，对应的根径值为6 cm，结合103株编表样本的根径分布幅度，确定巨尾桉根径-胸径对照表最小根径为6 cm，最大根径为30 cm。根据最优根径-胸径数学模型，代入根径值计算出胸径估计值。以1 cm作为径阶距，将全部根径径阶值导入上述模型进行计算，展开后即得到巨尾桉根径-胸径对照表(表5)。

4 巨尾桉一元材积表的编制

4.1 一元材积表的编制

表5 巨尾桉根径-胸径对照Tab.5 Root diameter-diameter breast height control of Eucalyptus grandis×E.urophylla

V=a + bD＾i+ cD＾i2+ dD＾i3

(10)

选择模型(10)进行回归分析，求解参数值a=0.056 922，b=-0.016 103，c=0.001 738，d=-0.000 015。将参数代入经验模型方程式(10)，以1 cm作为径阶距，将全部胸径估计值(D＾i)导入上述模型进行计算，展开后即得到巨尾桉胸径一元材积表(表6)。

表6 巨尾桉胸径一元材积表Tab.6 Unitary volume table of Eucalyptus grandis×E.urophylla

4.2 一元材积表的适用性检验

使用SPSS软件，采用回归分析曲线估计法对F检验方程进行拟合，参数估计值为：a=0.006 385，b=1.054 999。

将方程参数a、b值、样本数量m值及随机抽取用于检验的35株样木材积实际值和估计值代入公式，计算得F值为1.32，小于F0.05(1,33)的查表值4.14，检验结果表明，一元材积表可以在生产中使用。

5 结论

根据野外采集的根径、胸径成对数据，利用SPSS软件进行非线性回归分析，对备选的线性方程、对数方程、二次方程、三次方程、幂函数5个根径-胸径数学模型进行拟合并求解参数，除对数方程相关指数稍小(93%)外，其他4个方程的相关指数均达到95%以上，拟合效果都很好。其中，三次方程相关指数最大(96%以上)，拟合效果最好。5个方程相关指数均大于90%，足以证明巨尾桉人工林林木根径与胸径之间具有显著的相关关系。

经计算关键统计学指标进行综合评判，适用性检验结果予以佐证，三次方程：D=3.082534+0.080122DR+0.046354DR2-0.000920DR3适合作为巨尾桉根径-胸径数学模型，适用于双江县巨尾桉人工林。

研究编制的巨尾桉一元材积表：V=0.056922-0.016103D＾i+ 0.001738D＾i2- 0.000015D＾i3，通过适用性检验，达到了精度要求，可以在生产中使用。

研究编制的巨尾桉根径-胸径数学模型及一元材积表，为林业调查、林政执法等林业工作提供了较为合理的材积测算方法，对于利用残留的伐根测算被盗伐、乱伐的巨尾桉人工林蓄积以及测算正常采伐限额消耗均具有重要的应用价值[18]。