巨尾桉人工林立木材积表的编制
2022-06-13韦文长高德祥刘世雄刘明奎
韦文长,高德祥,刘世雄,刘明奎
(1. 双江县林业和草原局,云南 双江 677399; 2. 云南省林业调查规划院,云南 昆明 650051)
巨尾桉(Eucalyptusgrandis×E.urophylla)是以巨桉(EucalyptusgrandisHill ex Maiden)为母本、尾叶桉(EucalyptusurophyllaS. T. Blake)为父本培育而成的杂交种,继承了母本干形通直,萌芽能力强以及父本速生丰产的优良性状,是经营短周期工业原料林、生产优质木材和纸浆用材的优良树种。多年以来的生产实践证明,桉树具有生长快、轮伐期短、技术成熟、病虫害少以及经济效益好的优点[1],已成为目前木材短缺时代的重要商品林资源。当前,以巨尾桉为代表的速生桉产业得到大规模发展,为准确、高效地测算巨尾桉林分蓄积量,必须依靠高精度的蓄积量调查数表作为科学依据。因此,编制应用巨尾桉立木材积表,为巨尾桉人工林伐区设计、森林资源资产评估等调查工作提供准确的调查数表,在林业调查工作实践中十分重要。
在立木材积表的编制研究方面,法国的格纳得(Gurnand A, 1878)最早提出了材积表法[2],孟宪宇在《测树学》关于林分蓄积量测定方法中对材积表法进行了新的论述,即采用预先编制好的立木材积表来确定森林蓄积量的方法,阐述了在电子计算技术兴起的利好条件下,广泛采用材积回归方程来编制立木材积表的发展趋势,并为编制一元材积表和二元材积表分别提供了常用的材积回归方程。
国内在桉树调查数表的研究方面,韩培新、冯超以山本和藏式材积方程作为最优的编表模型,编制了韶关市尾巨桉和巨尾桉短周期工业原料林二元材积表[3];罗明永开展了尾叶桉人工林二元材积表的研制,确定了山本和藏式材积方程是最优的编表模型[4];广西壮族自治区林业局、广西区林业勘测设计院发布了《广西速丰桉数表》[5],其中的二元材积模型以山本和藏式材积方程为基础,以胸径、树高为变量设置可变参数,模型参数由山本和藏式的3个变为5个;冯强、方良以山本和藏式材积方程作为基本模型,对可变参数的动态模型进行了模型研建,建立了海南桉树立木材积模型[6];云南省林业调查规划院发布了赤桉(EucalyptuscamaldulensisDehnh.)、蓝桉(EucalyptusglobulusLabill.)和直干桉(EucalyptusmaideniF. V. Muell.)的山本和藏式二元材积模型参数。在国内桉树调查数表的研究成果中,尚未发现巨尾桉一元材积表的编制成果;在巨尾桉二元材积表的研究方面,由于地域自然条件和经营管理水平的差异,广东韶关市的巨尾桉二元材积表的编制成果也与云南省临沧市双江县的实际状况存在差异。因此,编制符合云南省自然条件和经营管理水平条件下的巨尾桉一元材积表和二元材积表,对于科学研究巨尾桉立木材积与胸径、树高的内在关系,科学管理巨尾桉人工林资源,促进产业科学发展等方面十分必要。
1 材料与方法
1.1 研究材料
1.1.1 材料的选择
研究材料来源于云南省临沧市双江县。根据《林业数表编制数据采集技术规程》对样本数量的相关要求[7],在不同立地条件下的3个巨尾桉人工林伐区,按照各径阶样木较均匀分布的原则,在6~22 cm径阶区间随机选取树干通直圆满、无分杈的巨尾桉样木138株,其中:建模样本103株,检验样本35株。样木收集地立地条件及样木株数见表1。
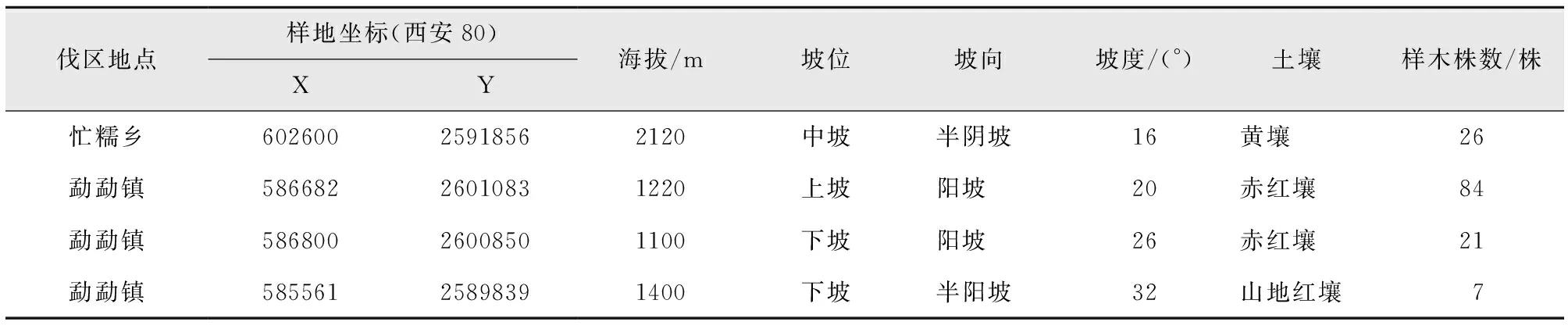
表1 双江县样木收集地立地条件及株数Tab.1 Sites and number of Eucalyptus grandis×E.urophylla samples in Shuangjiang County
收集样木的伐区涵盖坝区、半山区和高海拔山区,分不同的坡位、坡向、坡度和土壤,林分密度和经营管理水平均有差异,样木的选择具有较广的代表性。138株样木按径阶分布及树高统计详见表2。

表2 样木按径阶分布及树高统计Tab.2 Statistics of sample wood distribution according to diameter rank and tree height range
1.1.2材料的处理
样木伐倒后,用皮尺测量伐倒木的树高加上伐桩长度即为样木全株树高。采用2 m(树高10 m以上)或1 m(树高10 m以下)对伐倒木进行区分段造材,从树杆根部往上第一个区分段要包括伐桩。测量记录各区分段中央直径以及最后不足一区分段梢头底端直径和梢头长度。采用中央断面积区分求积法计算各区分段材积,采用圆锥体公式计算梢头材积。各区分段材积与梢头材积的总和即为样木的单株木总材积。
1.2 研究方法
1.2.1备选的材积方程
根据胸径一个因子与材积的回归关系编制的材积数表称为一元材积表,孟宪宇在一元材积表的编制方法上[2]提供了7个常用的一元材积回归方程,本课题选择其中的6个一元材积回归方程作为巨尾桉人工林一元材积回归方程的备选模型(表3)。

表3 备选一元材积回归方程Tab.3 Alternative unitary volume regression equations
式中:V为立木材积(m3);d为胸径(cm);a0、a1、a2为方程参数。
根据材积与胸径、树高两个因子的回归关系编制的材积数表称为二元材积表,孟宪宇在《测树学》关于二元材积表的编制方法上[2]提供了21个常用的二元材积方程,本课题选择了其中的9个二元材积方程作为巨尾桉人工林二元材积方程的备选模型(表4)。
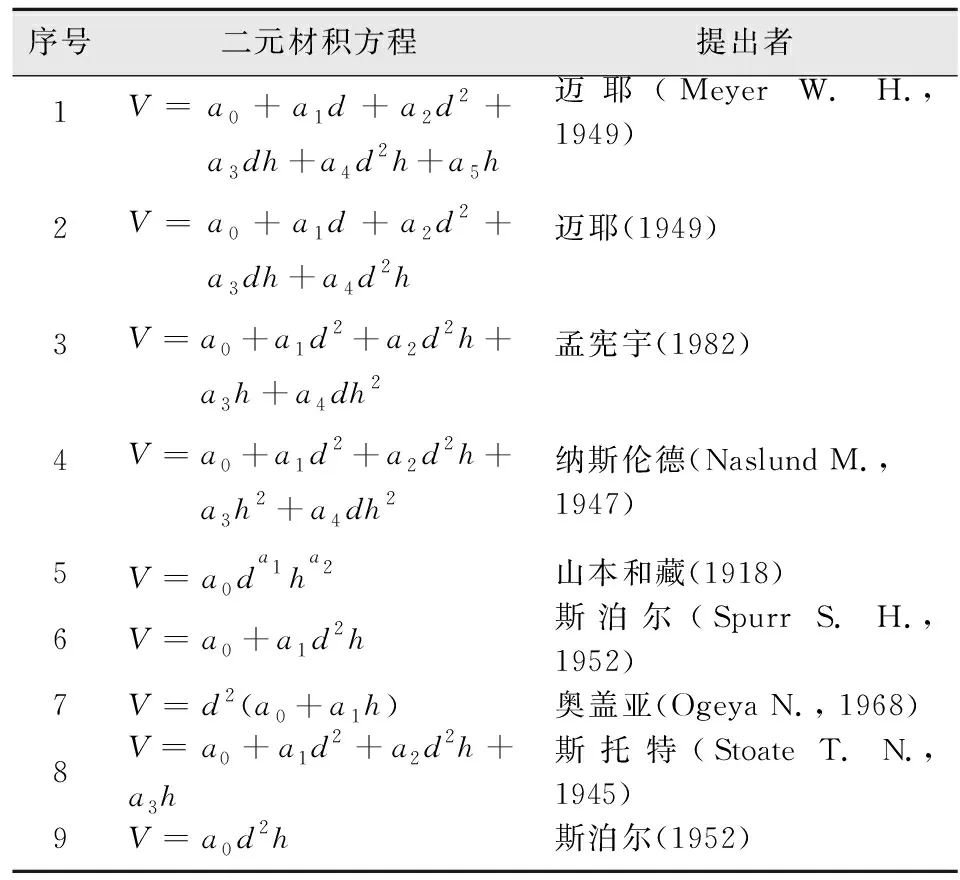
表4 备选二元材积方程Tab.4 Alternative binary volume equations
式中:V为立木材积(m3);d为胸径(cm);h为树高(m);a0、a1、a2、a3、a4、a5为方程参数。
1.2.2材积方程的拟合与评价
将103株建模样木数据代入各材积方程,使用SPSS软件Levenberg-Marquardt迭代法对各方程进行拟合并求解方程参数。根据各材积方程参数、样木胸径和树高数据计算出样木的一元材积和二元材积估计值,根据样木材积估计值和实际值之间的差异,一元材积模型的评价以离差平方和(SSR)、相关指数(R2)、总相对误差(RS)、相对误差平均值(REA)、相对误差绝对值平均值(REAA)和残差(SR)分布图作为评价指标[8];二元材积模型的评价以离差平方和(SSR)、相关指数(R2)、总相对误差(RS)、相对误差平均值(REA)、预估精度(P)和残差(SR)分布图作为评价指标[9]。各评价指标计算公式为:
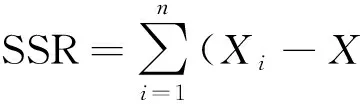
(1)
(2)
(3)
(4)
(5)
(6)
SR=Xi-X^i
(7)
式中:Xi为第i个样本的材积实际值;X^i为第i个样本的材积估计值;n为样本数;ta为置信水平a时的t分布值;T为回归模型的参数个数。
1.2.3最优编表模型的确定
根据各材积方程的拟合结果,综合评价材积方程的各项指标,选择离差平方和小、相关指数大、总相对误差小、相对误差平均值小、相对误差绝对值平均值小、残差图以横轴为中心分布均匀的材积方程作为一元材积表的最优编表模型;选择离差平方和最小、相关指数最大、总相对误差最小、相对误差平均值最小、预估精度最大、残差图以横轴为中心分布均匀的材积方程作为二元材积表的最优编表模型。
1.2.4编表模型的适用性检验
使用35株检验样本数据分别对一元材积表和二元材积表的编表模型进行适用性检验。若总相对误差(RS)在±5%范围内,同时通过F检验(F≤F0.05)时,则一元材积表的编表模型适用;若总相对误差(RS)绝对值小于等于3%、相对误差绝对值平均值(REAA)小于10%、残差图以横轴为中心分布均匀并通过F检验(F≤F0.05)时,则二元材积表的编表模型适用。
2 结果与分析
2.1 一元材积表的编制
2.1.1备选一元材积方程的拟合与评价
使用103株建模样本数据对备选的6个一元材积回归方程进行拟合并求解参数,计算各方程的评价指标,结果显示,离差平方和(SSR)最小的是6号模型中岛广吉式,相关指数(R2)最大的是6号模型中岛广吉式,总相对误差(RS)最小的是3号模型覆赫纳德尔(Hohenadl W.)-克雷恩(Krenn K.)式,相对误差平均值(REA)最小的是3号模型覆赫纳德尔(Hohenadl W.)-克雷恩(Krenn K.)式,相对误差绝对值平均值(REAA)最小的是6号模型中岛广吉式,各方程拟合结果详见表5。
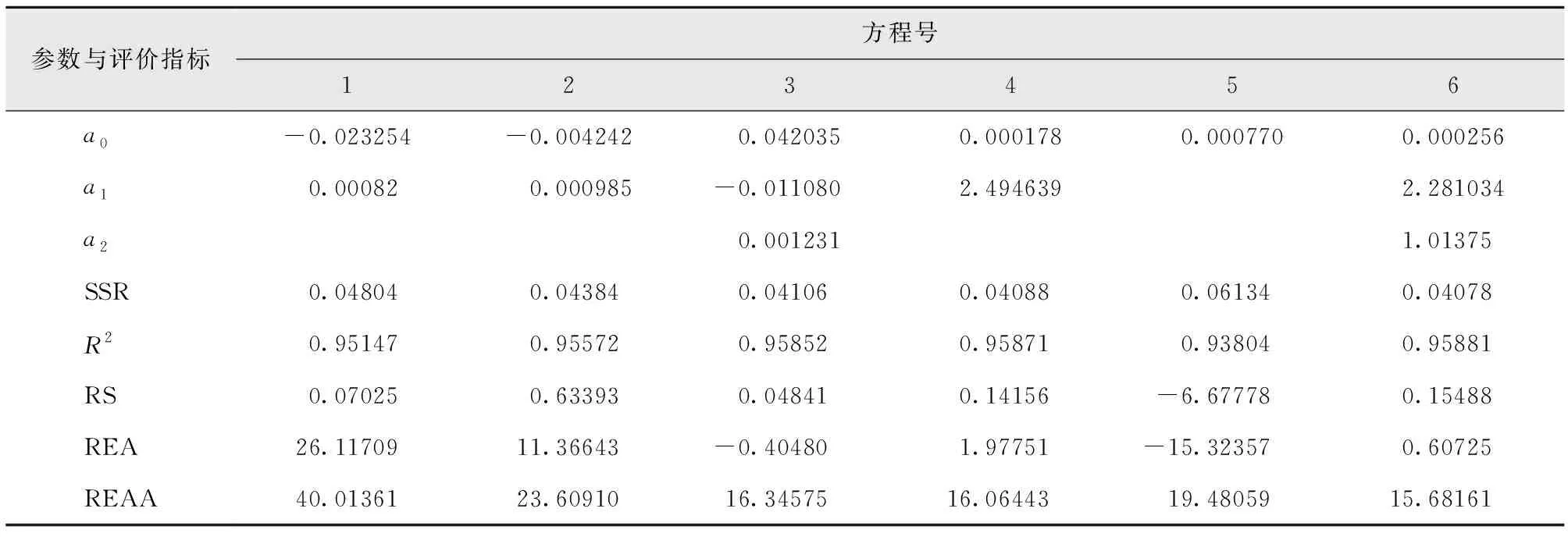
表5 备选一元材积回归方程参数及评价指标值Tab.5 Parameter and evaluation index values of alternative unitary volume regression equations
2.1.2最优编表模型的确定
将备选一元材积回归方程的各项评价指标值进行比较排序,根据各方程的离差平方和、相关指数、总相对误差、相对误差平均值和相对误差绝对值平均值这几项评价指标的综合得分评价结果,6号模型中岛广吉式综合误差最小,总得分排序最高。各方程综合得分及排序详见表6。
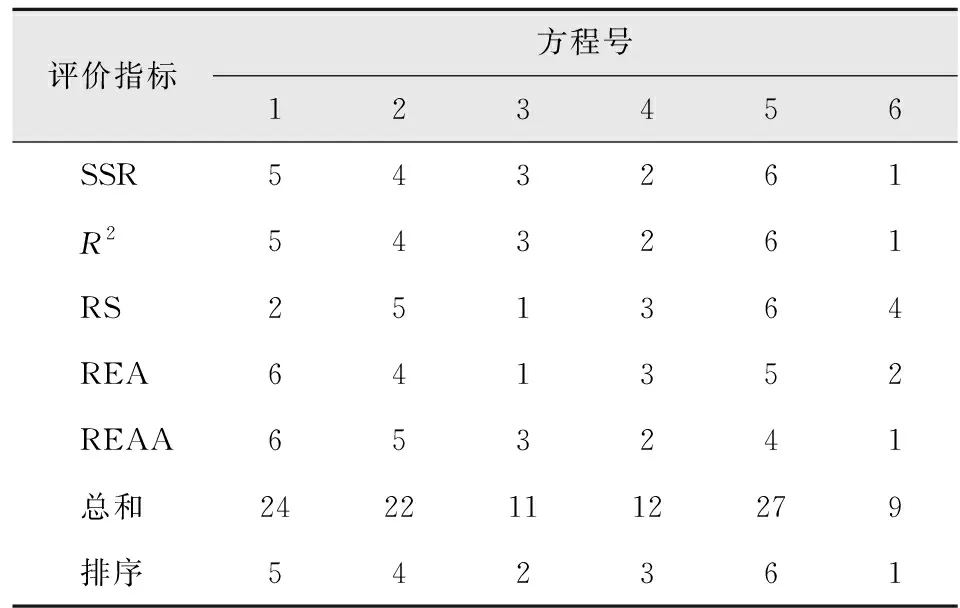
表6 备选一元材积回归方程综合得分及排序Tab.6 Comprehensive score and ranking of alternative unitary volume regression equations
以胸径为横轴、残差为纵轴绘制残差分布图,结果显示残差图以横轴为中心分布均匀(图1)。
根据以上评价指标分析结果,中岛广吉式是上述6个备选一元材积回归方程中拟合效果最好的方程,是编制巨尾桉一元材积表备选材积方程中最优的编表模型。
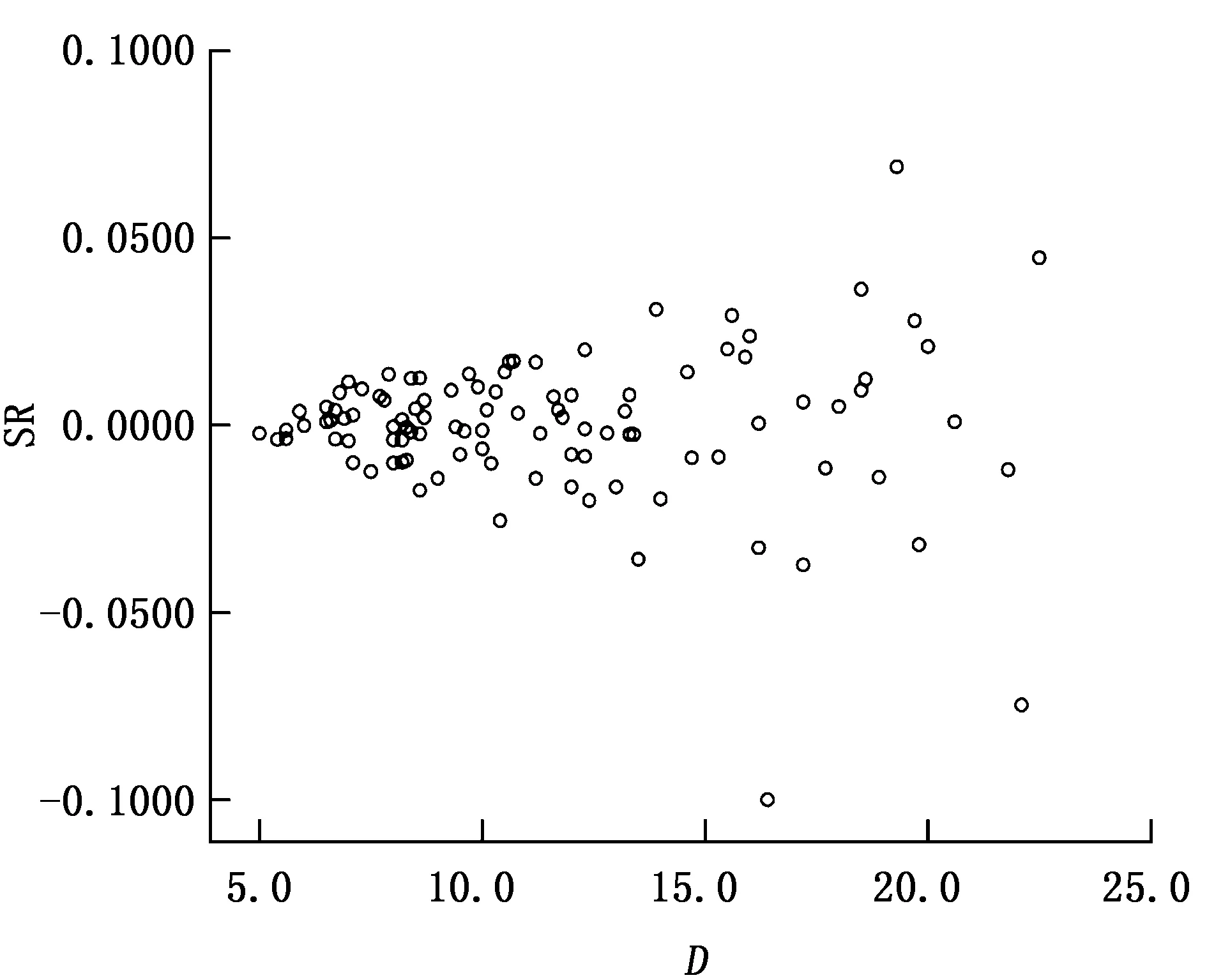
图1 中岛广吉式(6号模型)建模样本残差分布Fig.1 Residual distribution of Nakajima Hiroyoshi modeling sample (Model 6)
2.1.3编表模型的适用性检验
使用35株检验样本数据对中岛广吉式模型进行适用性检验,总相对误差(RS)为4.256 73%,在±5%的误差范围内;根据35株检验样本材积实际值和估计值的独立样本t检验结果,F统计量的观测值为0.027,小于F0.05(1,68)的临界值3.982,对应的概率P值为0.869,大于显著性水平0.05,认为材积实际值和估计值两总体方差相等;在方差相等条件下,对应的双尾概率P值为0.856,大于显著性水平0.05,表明材积实际值和估计值两总体样本无显著差异。
综合以上检验结果表明,中岛广吉式模型适合作为巨尾桉一元材积表的编表模型,拟合的模型公式为:
V=0.000256D2.2810341.01375D
(8)
2.1.4一元材积表的展开
将径阶中值代入一元材积模型公式(8),展开后即得到巨尾桉一元材积表(表7)。
2.2 二元材积表的编制
2.2.1备选二元材积方程的拟合与评价
使用103株建模样本数据对备选的9个二元材积方程进行拟合并求解参数,计算各方程的评价指标,结果显示,离差平方和(SSR)最小的是1号模型迈耶(Meyer W. H., 1949)式,相关指数(R2)最大的是1号模型迈耶(Meyer W. H., 1949)式,总相对误差(RS)最小的是8号模型斯托特(Stoate T. N., 1945)式,相对误差平均值(REA)最小的是2号模型迈耶(1949)式,相对误差绝对值平均值(REAA)最小的是2号模型迈耶(1949)式,预估精度最高的是1号模型迈耶(Meyer W. H., 1949)式。各方程拟合结果详见表8。
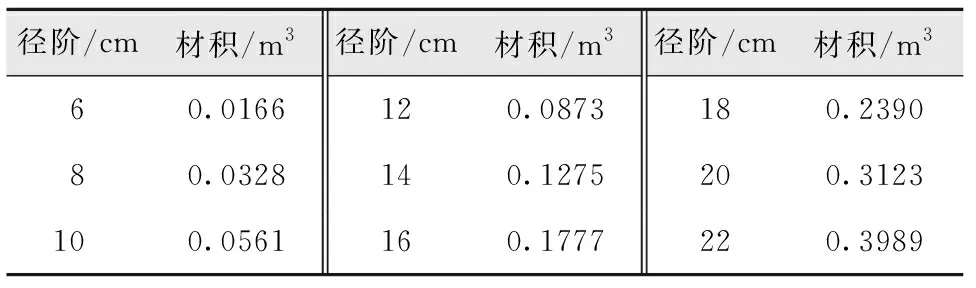
表7 巨尾桉一元材积表Tab.7 Unitary volume table of Eucalyptus grandis× E.urophylla
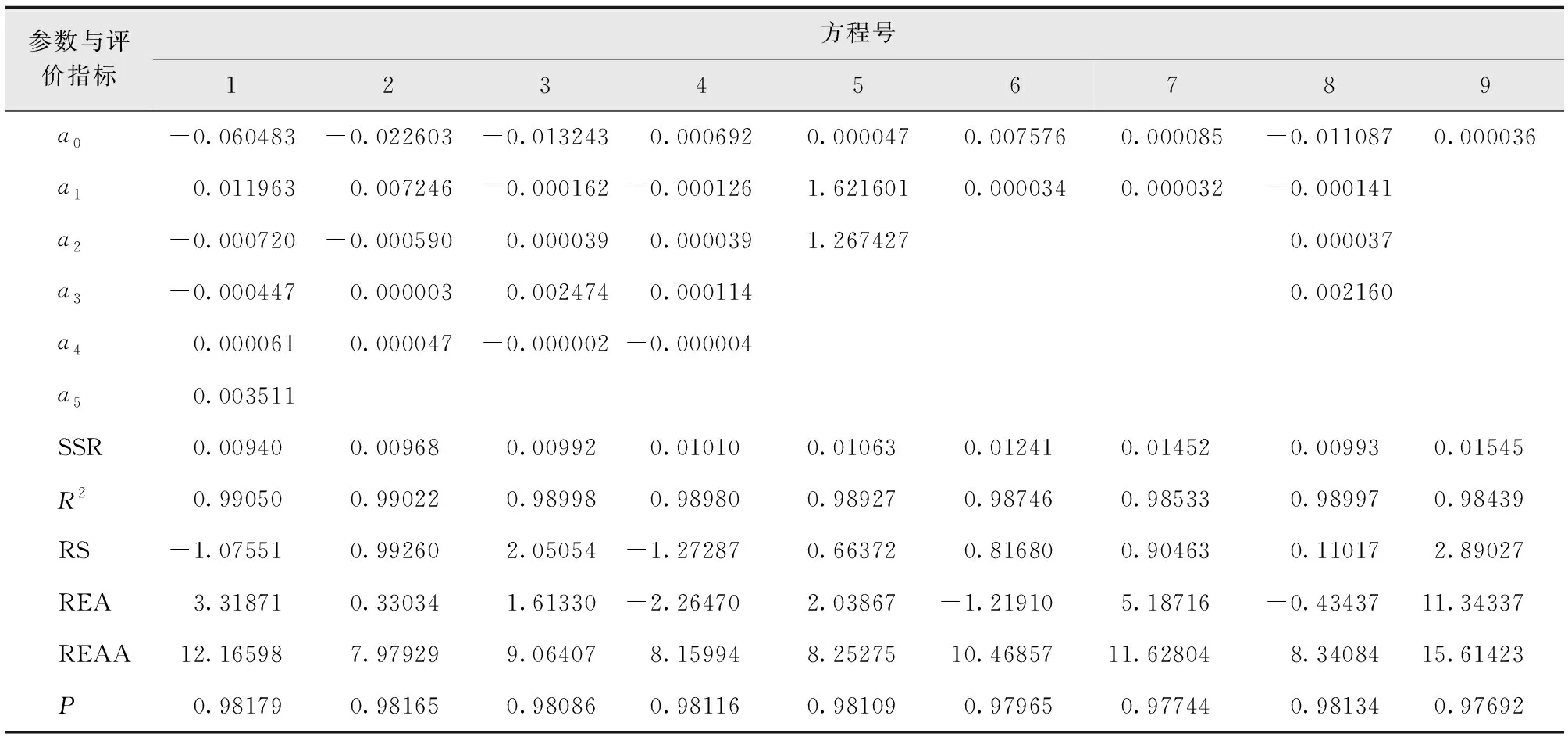
表8 备选二元材积方程参数及评价指标值Tab.8 Parameter and evaluation index values of alternative binary volume equations
2.2.2最优编表模型的确定
将备选二元材积回归方程的各项评价指标值进行比较排序,通过比较离差平方和(SSR)、相关指数(R2)、总相对误差(RS)、相对误差平均值(REA)和预估精度(P)这几项评价指标的综合得分,2号方程迈耶(1949)式综合误差最小,总得分排序最高,各方程综合得分及排序详见表9。以胸径为横轴、残差为纵轴绘制残差分布图,显示残差图以横轴为中心分布均匀(图2)。根据评价指标分析,2号方程迈耶(1949)式是9个备选二元材积方程中拟合效果最佳的二元材积方程,是编制巨尾桉二元材积表备选材积方程中最优的编表模型。
2.2.3编表模型的适用性检验
使用35株检验样本数据对迈耶(1949)式模型进行适用性检验,结果显示:总相对误差(RS)为0.325 06%,小于3%;相对误差绝对值平均值(REAA)为2.327 62%,小于10%;经残差分析,残差图以横轴为中心分布较为均匀(图3);根据35株检验样本的材积实际值和估计值进行独立样本t检验结果,F统计量的观测值为0.024,小于F0.05(2,67)的临界值3.134,对应的概率P值为0.877,大于0.05的显著性水平,认为材积实际值和估计值两总体方差相等;在方差相等条件下,对应的双尾概率P值为0.988,大于显著性水平0.05,表明材积实际值和估计值两总体样本无显著差异。
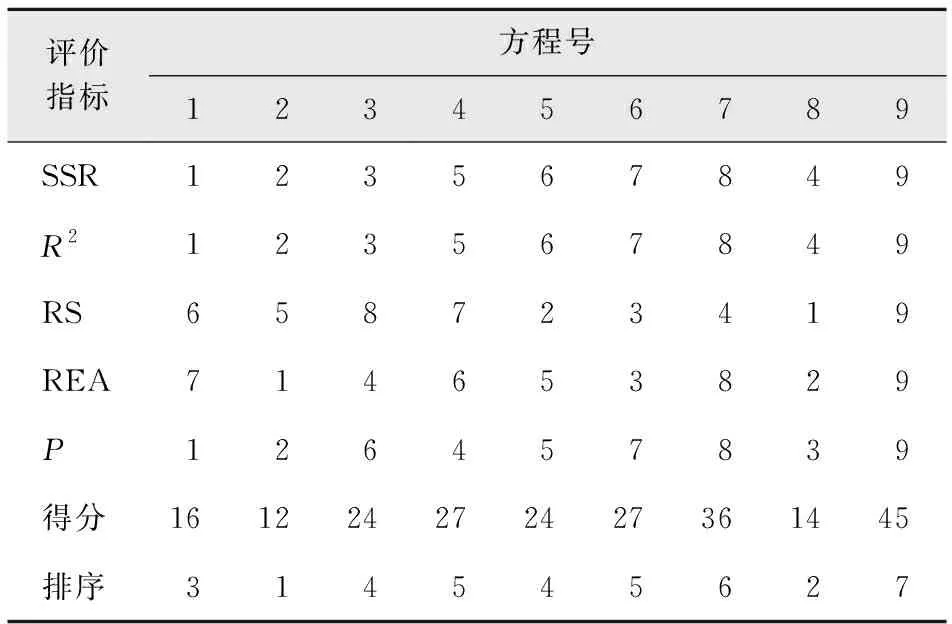
表9 备选二元材积回归方程综合得分及排序Tab.9 Comprehensive score and ranking of alternative binary volume equations
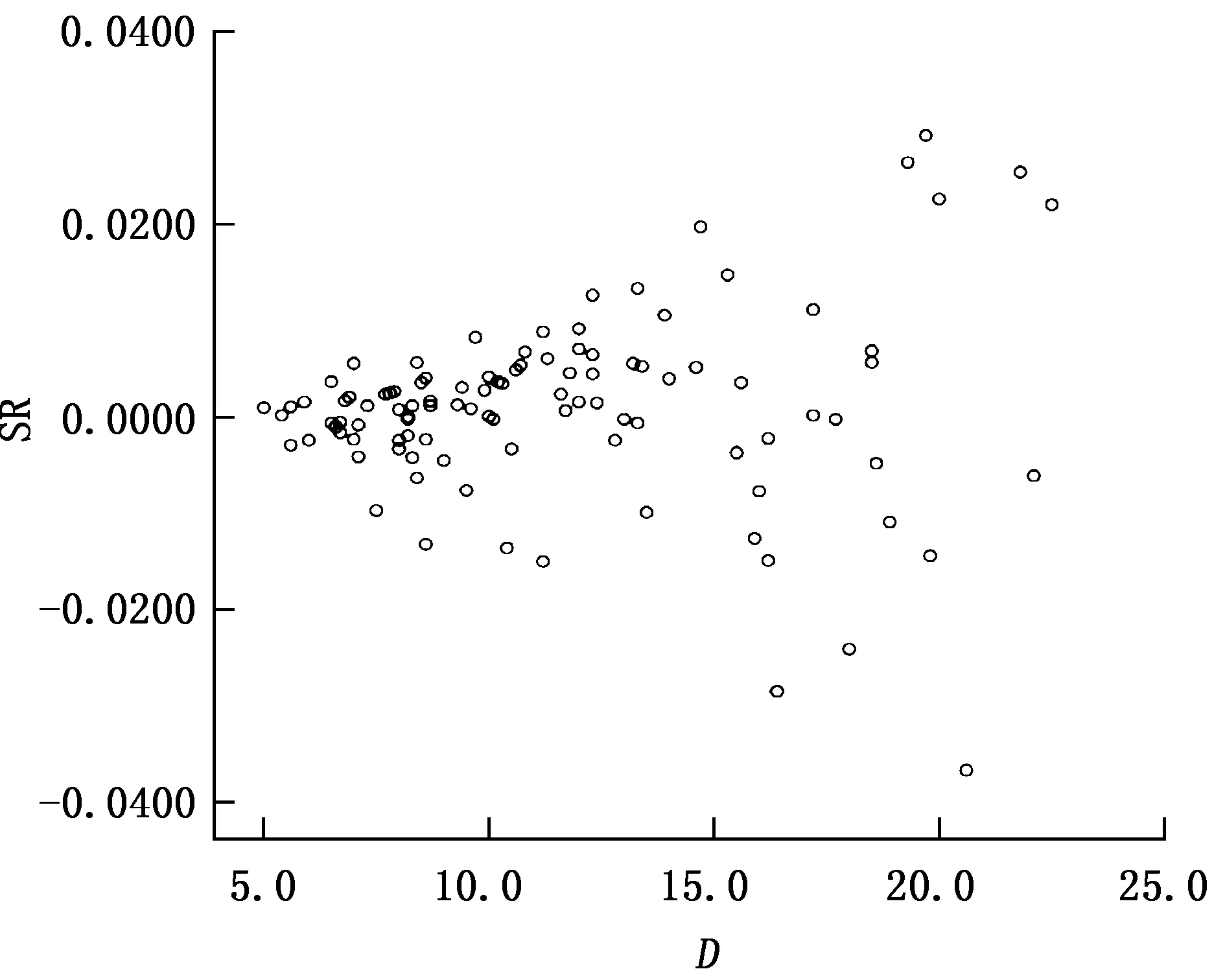
图2 迈耶(1949)式(2号方程)建模样本残差分布Fig.2 Residual distribution of Meyer (1949) modeling sample (Model 2)
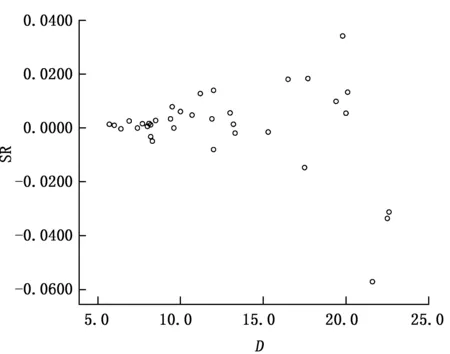
图3 迈耶(1949)式(2号方程)检验样本残差分布Fig.3 Residual distribution of Meyer (1949) test sample (Model 2)
综合以上检验结果表明,迈耶(1949)式模型适合作为巨尾桉二元材积表的编表模型,拟合的模型公式为:
V=-0.022603+0.007246D-0.00059D2
+0.000003DH+0.000047D2H
(9)
2.2.4二元材积表的展开
将径阶中值、树高值代入二元材积模型公式(9),展开后即得到巨尾桉二元材积表(表10)。
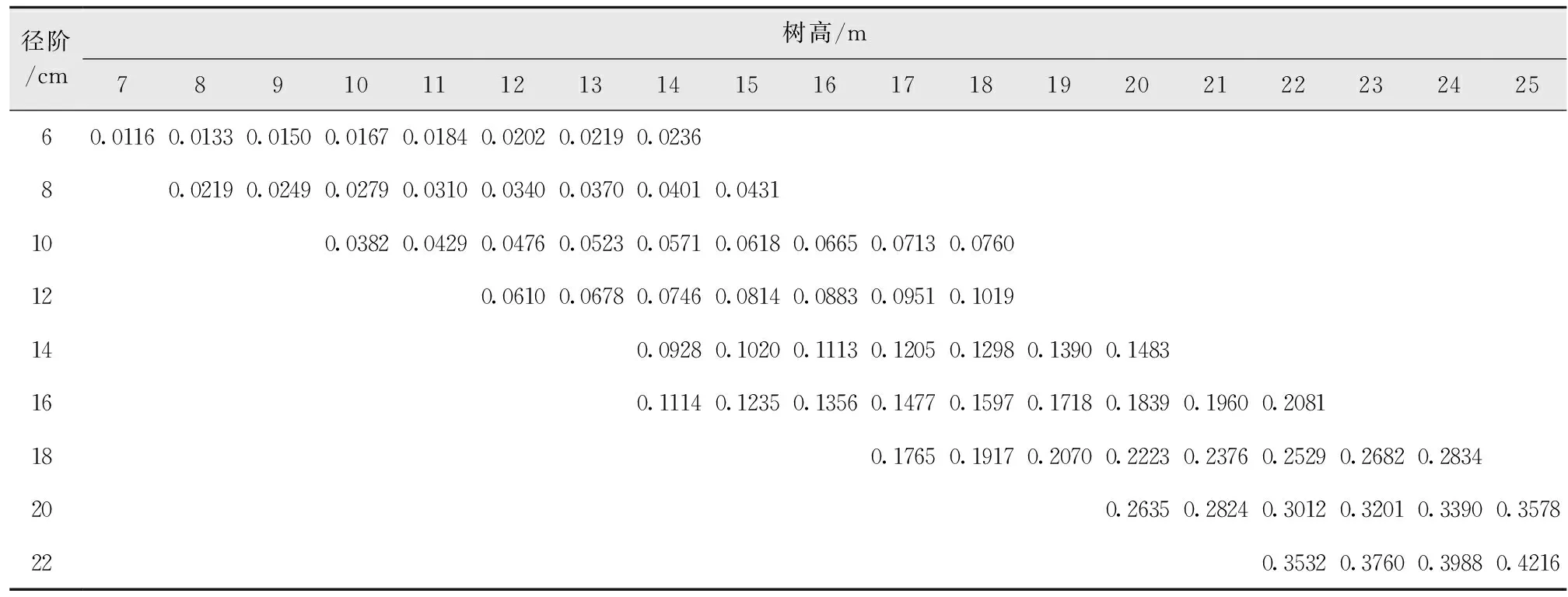
表10 巨尾桉二元材积表Tab.10 Binary volume table of Eucalyptus grandis×E.urophylla
3 结论与讨论
本研究根据《林业数表编制数据采集技术规程》对编制县级立木材积表在样木数量、径阶分布和立地条件等方面的技术要求进行样木采集,所采集的样木来自不同立地条件的伐区,经营管理措施各不相同,各径阶均涵盖了不同树高级样木,基本能够反映双江县巨尾桉人工林在不同自然条件和经营条件下的生长水平,符合林业数表编制关于样木采集的技术要求。
根据103株巨尾桉建模样本数据,以6个一元材积回归方程和9个二元材积方程作为备选的编表模型,利用Levenberg-Marquardt迭代法拟合,最优的一元材积表编表模型为中岛广吉式:V=0.000256D2.2810341.01375D,最优的二元材积表编表模型为迈耶(1949)式:V=-0.022603+0.007246D-0.00059D2+0.000003DH +0.000047D2H,两个编表模型均具有相关指数高、误差低的特点,且拟合效果良好。
根据35株检验样本数据的检验结果,中岛广吉式一元材积表编表模型和迈耶(1949)式二元材积表编表模型在误差、残差和F检验等指标方面均符合现行一元、二元立木材积表编制技术规程的技术标准,由以上两个编表模型编制而成的巨尾桉人工林一元材积表和二元材积表适用于双江县巨尾桉人工林森林资源调查。
一元材积表是以平均胸径为自变量,平均材积为因变量编制的数表,未考虑树高对材积的影响。事实上,相同胸径的林木因所处立地条件方面的差异,其树高是存在明显差异的。因此,一元材积表的缺点是使用范围较小,仅适用于立地条件相似的某一地区(县、区、林业局或林场)。其优点是方便快捷、野外调查工作量相对较小。二元材积表是根据材积与胸径、树高两个因子的函数关系编制的材积表,充分考虑了树高这一影响林木材积的重要因素,优点是不受立地条件的限制,使用范围较大。二元立木材积计算结果一定程度上反映了立地条件方面的差异。因此,相比较而言,二元立木材积编表模型计算得到的立木材积精度更高,与实际情况更吻合。
本次研究随机选取的巨尾桉样木138株(其中:建模样本103株,检验样本35株)分布于双江县全境,其生境涵盖了双江县不同的立地条件,检验结果也足以证明所编制的巨尾桉人工林一元材积表和二元材积表在双江县的适用性。至于双江县巨尾桉人工林蓄积调查时是选择一元材积表,还是选择二元材积表,更多需要考虑的是调查精度的要求。对于森林资源连续清查等精度要求较低的蓄积量调查工作适宜选择使用一元材积表,对于林木采伐设计、森林资源资产评估、森林火灾查勘定损等精度要求较高的蓄积量调查工作适宜选择使用二元材积表。
在开展巨尾桉人工林标准地每木检尺调查工作中,可以实测一定数量不同径阶的样木胸径和树高,根据树高与胸径的最佳回归关系式,计算检尺木胸径对应的树高值(胸径和树高均保留一位小数),代入迈耶(1949)式二元材积表编表模型:V=-0.022603+0.007246D-0.00059D2+0.000003DH+0.000047D2H,可以获得更高精度的蓄积量调查数据。
