雨天条件下车辆轮胎与沥青路面间附着特性

马 涛， 汤钧尧， 郑彬双， 黄晓明

(东南大学交通学院， 南京 211189)

据世界卫生组织最新《全球道路安全现状报告》统计，道路交通伤害已成为第八大死因，年死亡人数持续攀升，已达135万人，追尾、侧滑等因为轮胎和路面之间摩擦力不足是引发交通事故的主要原因[1-3]. 同时，雨雪天造成沥青路面潮湿或积水，车辆轮胎高速驶过路面时路面黏附的薄层水膜影响了胎面与路面的有效接触面，流体动力润滑作用使得轮胎相对于粗糙路面发生了一定程度的滑移，产生滑水现象[4]，严重情况下会影响轮胎的湿牵引力下降甚至是失效，威胁到车辆行驶的安全性及操纵稳定性. 有研究表明，雨雪天气的交通事故率比平时高出5倍以上. 而由于胎面花纹块和路面纹理的存在，轮胎- 路面接触时接触面积发生变化，接触区域的任何部分产生的最大摩擦力不同，随着行驶速度提高轮胎与路面之间附着力急剧下降，导致制动过程中轮胎常发生滑移现象[5]. 因此，研究雨天条件下胎路间附着特性具有很强的现实意义和参考价值[6].

国内外主要从胎路模型建立以及附着系数计算着手，如Gim[7]提出轮胎稳态UA模型. Dugoff等[8]假定轮胎与路面接触区为矩形，根据接触区弹性变形得到轮胎纵向力随纵向滑移率的变化过程. Novikov等[9]介绍了一种基于路面附着系数的车辆制动研究方法，可测试事故调查中汽车发生打滑时路面附着系数. Ma等[10]基于单个轮胎回正力矩分配提出了一种轮胎- 路面附着系数预测方法，路面附着系数可借助系数识别规则确定. 黄晓明等[11]建立了橡胶胎面与柔性路面摩擦接触的数值分析模型，探讨了车辆处于自由滚动、紧急制动过程中胎面、路表变形特征及接触应力分布状态. 李德涛等[12]基于轮胎侧偏角和轮胎回正力矩信息设计路面附着系数估计器，构建路面附着系数评估函数. 常群等[13]基于路面附着系数建立了估计多路况安全距离的模型. 朱兴一等[14]从飞机着陆的安全性考虑，基于CEL法建立了考虑真实路表纹理的三相耦合模型，分析了不同因素对机轮滑水行为的影响规律. 周海超等[15]利用谐波叠加法建立三维粗糙路面模型，采用“伪”流体动力轴承作用等效反映路面水膜“密封”作用，提出了考虑多因素作用下轮胎与湿路面之间摩擦特性的仿真方法.

关于附着特性的研究，大多是将轮胎模型简化为力学元件或者基于经验数据推导，未从接触机理方面分析轮胎与粗糙路面的接触特性，至于附着系数的变化特点以及影响因素还需深入探究[16-17]. 更重要的是，潮湿路面上水膜的存在使得路面附着力显著变小，轮胎在较高行驶速度下极易发生打滑现象. 但大多数研究并未考虑水膜的影响，因此，本文基于轮胎的滑水机理，采用课题组前期建立的基于耦合欧拉- 拉格朗日方法的轮胎- 流体- 路面三相耦合模型，探讨了雨天条件下车辆行驶安全性的关键影响因素，分析水膜厚度变化因素对胎/路附着系数影响规律，为后续雨天车辆制动稳定性分析提供指导参数.

1 轮胎- 流体运动特性及润滑作用

1.1 路表弹性流体动力润滑机理

当车辆在有水膜路面上高速行驶时，水膜在荷载作用下对轮胎接触面产生一定的托举力，使得轮胎与水膜接触部分甚至全部脱离路面，形成滑水现象[18]. 研究表明，车轮荷载作用下引起滑水的主要因素为行车速度、道路状况(粗糙度、路面类型及水膜厚度等)与轮胎参数(花纹构造、橡胶材料黏弹性、胎压与荷载)[19].

在车辆外荷载作用下，胎- 路接触部位发生了局部弹性变形，形成了位于润滑表面之间的水膜形状，这个水膜形状产生的流体动压力可以视为橡胶胎面发生弹性形变的作用力，此时的动力润滑状态即为弹性流体动力润滑现象. 雷诺一维流动方程

(1)

为流体润滑理论的基础[20].式中：h为粗糙接触表面任意位置处流体膜厚；dp/dx为流动方向的压力梯度；U为界面入口处流体线速度；h0为流体压力最大处膜厚；υ为动力黏度.

假设滑水时轮胎不发生横向偏移，则轮胎挤压水流即可转化为平面问题，选取胎- 路间的流体微单元进行受力状态分析，如图1所示.在x方向受力平衡条件下，存在

(2)

图1 轮胎与路面间润滑模型Fig.1 Lubrication model between tire and pavement

单位体积内流量的质量可以表示为mx=ρqx，路表水流在轮胎荷载作用下从x、y、z三个方向流进与流出，根据质量守恒，可知特定时间内流体变化的质量差与密度变化引起的质量增量相同；同时，润滑模型中y方向流量变化不考虑，可得

(3)

联合得到等温条件下的雷诺方程

(4)

式中：U1、U2分别为轮胎、路面沿x方向的运动速度.实际上，恒温的润滑体系中，流体密度不变且水流挤压效应忽略不计，故式(4)简化为

(5)

即为恒温状况下，雨天行车过程中路表弹性流体动力润滑模型的表达式.

1.2 轮胎- 流体- 路面滑水理论模型

鉴于轮胎与路表之间的水流遵循伯努利定理，在轮胎挤压水流过程中要考虑橡胶轮胎的黏弹性变形与流体动水压力作用.根据黏弹性材料的力学基本方程[21]并经过LaPlace反变换得到橡胶轮胎在集中荷载p作用下的形变为

(6)

式中：dA为胎面橡胶单元的某一网格区域；p为水膜表面压力；ρ为橡胶轮胎表面各点距离网格区域中心的距离.考虑轮胎荷载与硬质路表两者的挤压效应，水流产生了动水压力，其流动特征遵循Reynolds方程，具体表达形式为

(7)

边界条件为

p(x,y,t)=0；∂p(x,y,t)/∂n=0；
h(x,y,0)=h0|t=0

式中：v′为橡胶单元对路表的相对滑移速度；p为水膜在挤压过程中产生的动水压力，且p=p(x,y,t)；υ0为液体运动黏度；h0|t=0为初始橡胶单元的位置.令h0为胎面初始未变形表面高度，h1为橡胶单元面的垂直变形，则水膜厚度h方程为

h=h0(t)+h1(x,y,t)

(8)

可知，作用时间和相对滑移速度可以通过车辆行驶状况确定，从而影响动水压力最关键的因素即为水膜厚度.轮胎在发生完全滑水时路表水膜存在一临界值，即为临界水膜厚度hcrit，临界水膜厚度的确定是分析其潮湿状态的前提.

2 轮胎滑水有限元模型

2.1 轮胎滑水模型的建立

轮胎滑水过程分析主要反映在轮胎与路面竖向接触力变化，为了提高模拟精度与深入揭示滑水时轮胎的动力学特征，后续采用滑水模型讨论轮胎滑水过程中受力情况. 由于轮胎受到水流动水压力作用会产生较大应变，且轮胎与水流呈现复杂的耦合动力变形，为了分析轮胎在一定厚度水膜上滑水问题本文采用耦合欧拉拉格朗日(coupled Eulerian Lagrangian，CEL)技术进行网格划分，从而避免了拉格朗日方法中由于快速流场引起的网格畸变缺点.

在此过程中，轮胎模型和流体模型分别使用拉格朗日单元和欧拉单元表示，2种模型单元间使用广义接触定义.约束流体模型底部在x方向上的自由度、两侧在y方向的自由度，参考路面平移速度，对水流区域施加负z方向的速度，使路面与水流速度一致，对整体模型施加x方向的重力场，得到轮胎滑水模型，如图2所示.

图2 基于CEL法轮胎滑水模型Fig.2 Tire hydroplaning model based on CEL method

路面潮湿状态下，由于水膜动水压力作用，此时的轮胎荷载由地面反力与动水压力的竖向分力共同承担，轮胎与粗糙路表之间的附着系数理论计算模型通常采用

(9)

式中：φ为干燥路面附着系数；Fd为水流拖拽力；Fh为轮胎荷载；Fz为轮胎滚动阻力；Ft为水流托举力.

2.2 轮胎滑水模型的验证

通常认为，轮胎开始处于完全滑水状态时(即轮胎与路面的竖向接触力为0时)对应的行驶速度为轮胎滑水临界速度，轮胎滑水临界状态如图3(a)所示. 将NASA经验公式[22]计算的滑水临界速度作为初速度，不断地调整轮胎滚动速度模拟不同充气压力下轮胎发生滑水时临界速度，并与NASA经验公式计算得到的滑水速度进行对比，如图3(b)所示.

图3 轮胎滑水模型验证结果Fig.3 Validation of the tire hydroplaning model

由轮胎滑水速度变化曲线可知，随着轮胎充气压力不断增大，轮胎发生临界滑水的速度逐渐增大，且与轮胎压力的平方根值呈线性变化，回归分析得到轮胎滑水速度数学表达式为vcrit≈8.06P0.5，与NASA公式描述的曲线变化相一致，但是系数略高于NASA表达式，这是由于轮胎花纹参数、路面纹理特性的差异性导致的，但模拟的临界滑水速度均在误差允许范围内. 鉴于此，论文基于ABAQUS建立的轮胎滑水有限元模型具有一定的准确性，可用于后续轮胎滑水影响因素的分析.

3 潮湿沥青路面状态界定

3.1 路表临界水膜厚度计算

根据上文对轮胎- 流体- 路面滑水模型的研究探讨，可知车辆发生滑水时存在临界速度，在其他参数不变条件下行驶速度小于临界速度时不发生滑水现象.

基于课题组建立的轮胎滑水有限元模型[23-25]，保持轮胎荷载3.922 kN与充气内压250 kPa不变，分析不同沥青路面上水膜厚度(hw)对临界滑水速度(vc)的影响. 考虑到实际滑水风险及水膜厚度大于6.0 mm时车辆在速度限值内已经完全处于滑水状态[18]，故调整水膜厚度在0～6.0 mm内变化，根据轮胎“水漂”定义即认为轮胎与地面的接触力为0时的最小行驶速度为临界滑水速度. 为了更直接体现路面水膜厚度对临界滑水速度的影响规律，绘制曲线，如图4所示.

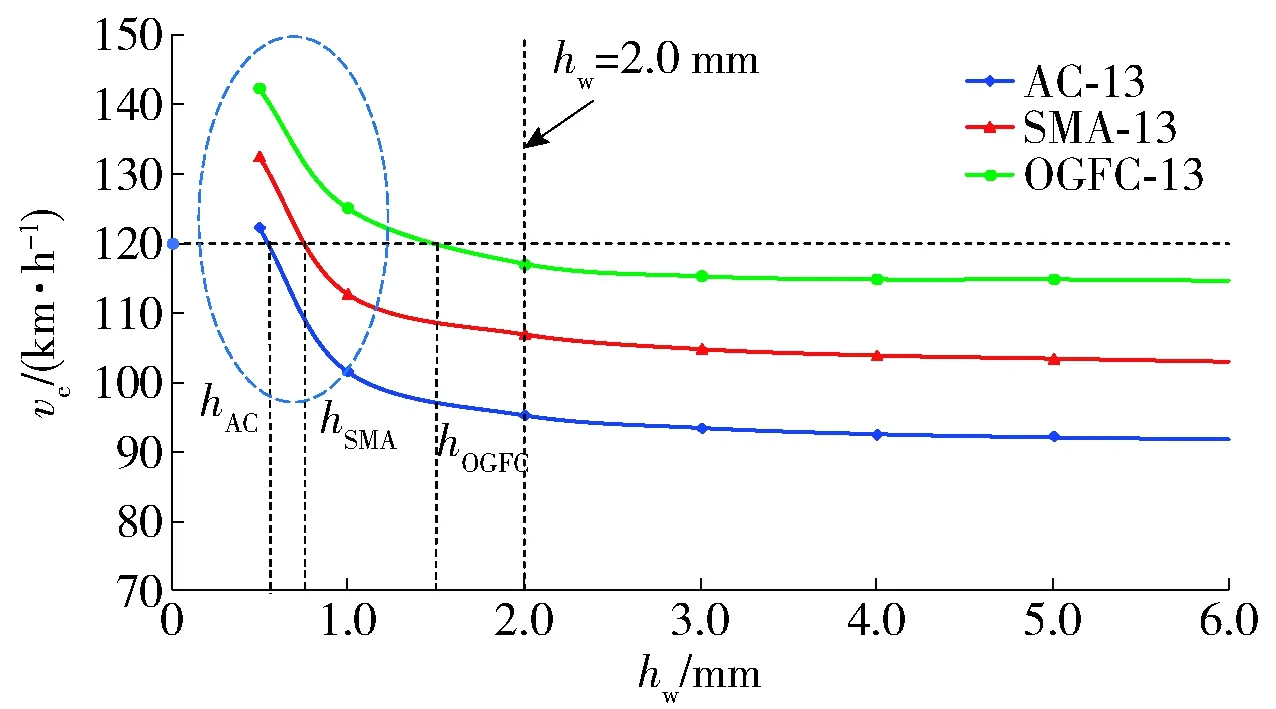
图4 不同水膜厚度时轮胎临界滑水速度Fig.4 Critical water skiing speed of tire with different water film thickness

由图4可知，在一定水膜厚度范围内，3种典型沥青路面的临界滑水速度变化趋势总体一致，当水膜厚度在0～2.0 mm时行车临界滑水速度变化速率较大，当水膜厚度大于2.0 mm时曲线趋于稳定；在国内规定的安全行驶速度限值120 km/h行驶时，不同沥青混合料类型的路面其不发生滑水的临界水膜厚度hcrit分别为AC 0.56 mm、SMA 0.76 mm、OGFC 1.50 mm.

3.2 沥青路面状态界定

依据胎- 路接触机理及路表流体润滑理论可以发现，在出现临界水膜厚度之前路表抗滑性存在极限最小值，此种情况下路表微凸体被水膜完全包裹，轮胎所受摩擦阻力几乎全部来自于润滑介质(水)的黏滞力，即为行车中潮湿路面抗滑性能最差的极限状态，将此临界状态称为潮湿与积水路面状态的分界线[26]. 鉴于此，需要从微观接触理论出发对水膜厚度小于1.0 mm的轮胎- 流体- 路面之间附着特性进行细化.

给予轮胎初速度为60 km/h，其他参数不变，调整滑水模型中水膜厚度参数，分析水膜厚度0～1.0 mm内对路表附着系数的影响，得到路面附着系数随水膜厚度的变化曲线，如图5所示. 根据附着系数变化曲线可以分为3个阶段.

1) 水膜厚度在0～0.2 mm变化时处于边界润滑阶段，流体润滑作用很小，路表微凸体均处于贡献率很大，路表摩擦力取决于路表粗糙微凸体与橡胶轮胎之间的摩擦.

2) 水膜厚度在0.2～0.5 mm变化时处于混合润滑阶段，路表微凸提部分被水膜阻隔成为摩擦“无贡献区”，此时的路表摩擦特性由流体黏性及粗糙表面介质共同决定.

3) 水膜厚度处于0.5～1.0 mm时属于弹性流体润滑阶段，此时路表微凸体被水膜完全淹没，但是路表水膜厚度较小，未产生动水压力[27].

图5 水膜厚度- 附着系数变化曲线Fig.5 Variation curve of water film thickness-adhesion coefficient

综上分析，结合弹性流体动力润滑理论并按照水膜厚度大小可将路面状态分为4种情况，其相应附着系数取值情况如下.

1) 干燥状态：hw=0 mm，附着系数取决于路表接触面纹理特性.

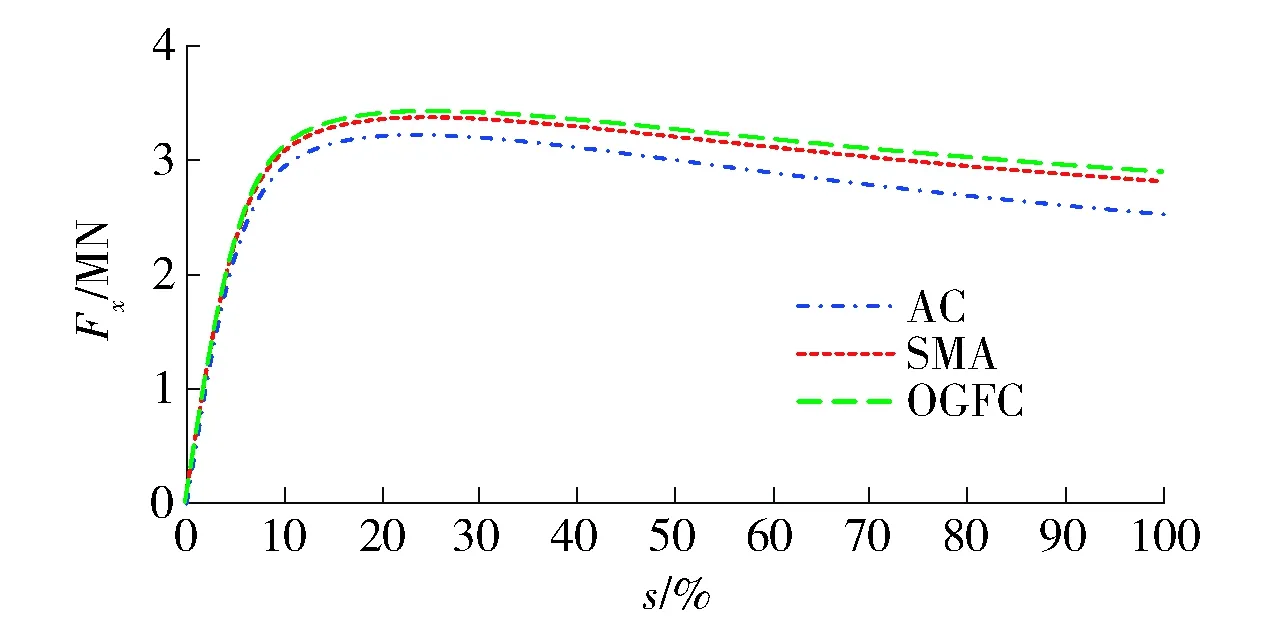
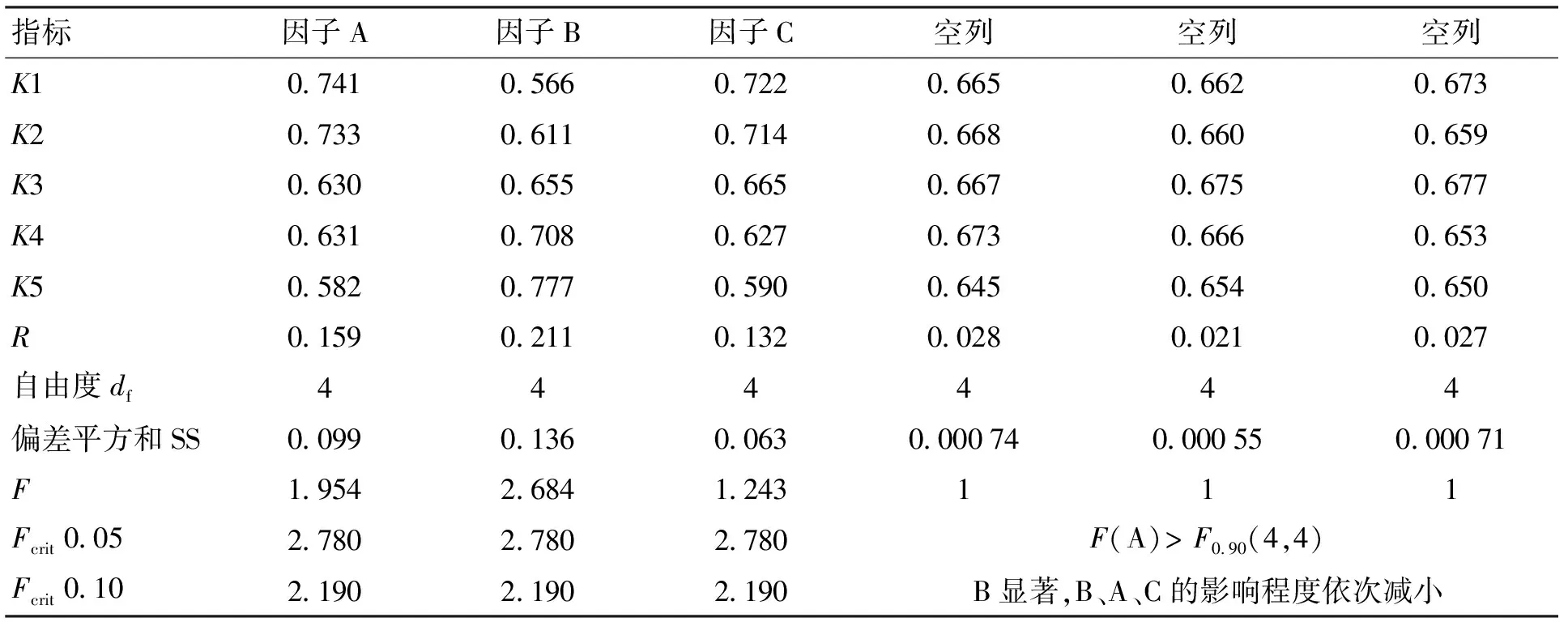
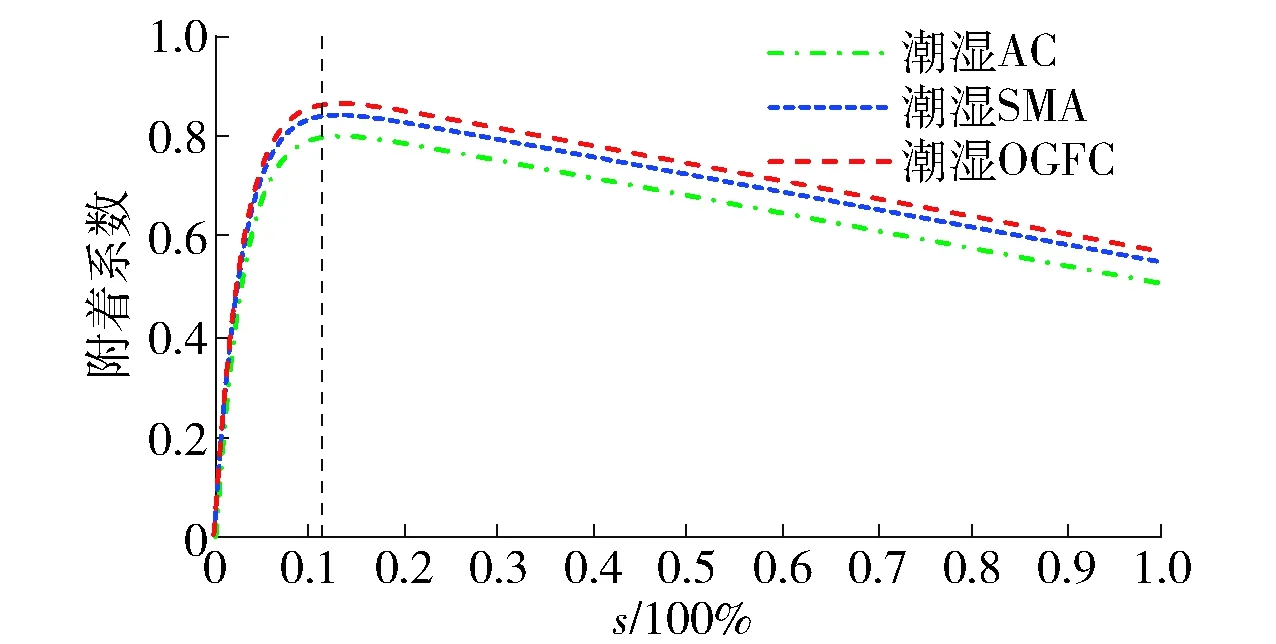
2) 潮湿状态：0

3) 润滑状态：0.5 mm

4) 积水状态：hw>1.0 mm，轮胎所受附着力完全取决于流体黏滞阻力，此时轮胎存在滑水的可能性.

4 路面峰值附着系数变化分析

4.1 不同影响因素下附着系数变化规律

根据潮湿路面附着力来源，需要先分析潮湿状态下轮胎动力学特征. 基于已建立的轮胎- 水流- 路面三相耦合模型，在ABAQUS自定义程序中输入潮湿状态路面摩擦因数函数，然后在稳态分析模块中调整轮胎滑移率得到潮湿条件下纵向力变化曲线，如图6所示.

图6 轮胎纵向力- 滑移率变化曲线Fig.6 Variation curve of tire longitudinal force-slip rate

由图6可知，轮胎滑移率0～5%内3种沥青路面上轮胎纵向力几乎相等；当滑移率大于5%时，随着滑移率逐渐增大潮湿沥青路面上轮胎纵向力由大到小依次为OGFC、SMA、AC，表明较高速度下水流润滑作用在胎- 路接触力占主导地位，同时水膜覆盖在粗糙路表上阻碍了轮胎与路面的接触，使得粗糙路面的宏观纹理提供的附着力被削弱，路表受到流体润滑作用使得相同行驶速度下的路面间附着力显著减小，轮胎产生的纵向力越小.

考虑不同类型沥青路面水膜厚度的影响因素(行车速度大小、宏观纹理参数及降雨量等)[30]，模拟计算不同水膜厚度下路面附着系数，得到各水膜厚度下附着系数曲线，如图7所示. 可知，一定宏观纹理参数、行车速度条件下，随着水膜厚度增大路面附着系数逐渐减小. 当水膜厚度hw≤1.0 mm时，路面附着系数较大且随着宏观纹理增加附着系数变化率较高，当水膜厚度hw>1.0 mm时，路面附着系数逐渐减小且路表宏观纹理影响程度迅速降低，表明水膜厚度大于1.0 mm时(积水状态下)，此时路表附着特性主要取决于水流的黏滞力.

图7 不同水膜厚度下路表附着系数曲线Fig.7 Adhesion coefficient curves with different water film thickness under wet road state

4.2 附着系数影响因素显著性分析

基于上述对路面附着特性影响规律的探究，采用正交试验设计进行多因素下参数显著性分析，以水膜厚度(因子A)、路表宏观纹理MPD值(因子B)、行车速度(因子C)3种因素为主要研究对象，各因素分别选取5因子水平，具体试验方案列如表1所示，极差计算结果如表2所示.

根据表2可知，各因子影响程度由大到小依次为B、A、C，路表纹理MPD值影响最显著，其次为路表水膜厚度，表明水膜厚度在较小时路表附着力主要由路面宏观纹理提高，水膜厚度较高(hw≥1.0 mm)时路表附着力大小主要由流体黏滞力提供，轮胎与路面之间受到流体润滑作用，存在滑水的风险.

4.3 潮湿沥青路面峰值附着系数曲线

基于以上潮湿路面附着特性的影响因素分析，可知潮湿状态时(0

表1 正交试验设计方案及结果

表2 路面附着系数极差分析

图8 潮湿路面附着系数- 滑移率曲线Fig.8 Adhesion coefficient-slip ratio curve of wet pavement

结果表明，滑移率在11.5%左右时附着系数曲线出现峰值点. 控制滑移率在11.5%左右，分析得到不同速度下路面峰值附着系数，拟合得到不同路面类型的峰值附着系数变化曲线，如图9所示. 可以发现，不同速度下峰值附着系数曲线呈“凸”型抛物线分布，随速度提高峰值附着系数逐渐减小. 这是因为较高速度下轮胎滚动半径变大，胎/路接触面积减小，路面提供的附着力减小. 显然地，潮湿路面峰值附着系数略低于干燥路面，主要是路面纹理的贡献率决定的，获取的峰值附着系数曲线对路面抗滑的研究具有重要意义.

图9 不同行车速度下路面峰值附着系数曲线Fig.9 Peak adhesion coefficient curve of pavement under different loads

5 结论

基于路表水流润滑理论深入探讨了潮湿路面上轮胎- 路面的接触机理，对不同水膜厚度下的轮胎临界滑水速度进行了界定，考虑不同类型沥青路面水膜厚度的影响因素(行车速度大小、宏观纹理参数及降雨量等)并模拟分析得到了不同路面水膜变化情况对沥青路面附着系数的影响规律.

1) 当水膜厚度在0～2.0 mm内时，行车临界滑水速度变化速率较大，当水膜厚度大于2.0 mm时曲线趋于稳定；安全行驶速度条件下(120 km/h)，不同沥青混合料类型的路面其不发生滑水的临界水膜厚度分别为AC 0.56 mm、SMA 0.76 mm、OGFC 1.5 mm.

2) 结合弹性流体动力润滑理论并按照水膜厚度大小可将路面状态分为4种情况：干燥状态(hw=0 mm)、潮湿状态(01.0 mm).

3) 一定宏观纹理参数、行车速度条件下，随着水膜厚度增大路面附着系数逐渐减小. 当水膜厚度hw≤1.0 mm时，路面附着系数较大且随着宏观纹理增加附着系数变化率较高；当水膜厚度hw>1.0 mm时，路面附着系数逐渐减小且路表宏观纹理影响程度迅速降低.

4) 采用正交试验设计理论分析了潮湿路面最显著影响因素，可知路表纹理MPD值影响最显著，其次为路表水膜厚度、行车速度，表明水膜厚度较小时路表附着力主要由路面宏观纹理提高，水膜厚度较大(hw≥1.0 mm)时路表附着力大小主要由流体黏滞力提供.

5) 潮湿状态下，滑移率在11.5%左右时胎路间附着系数曲线出现峰值点；不同沥青路面类型的峰值附着系数曲线呈“凸”型抛物线分布，且随速度提高峰值附着系数逐渐减小.

研究获取的峰值附着系数曲线对路面抗滑的研究具有重要意义，为后续雨天车辆制动稳定性分析提供指导参数，进一步为道路表面层选择决策、雨天交通管理控制提供依据.