基于抢占型离散排队的军事信息服务系统性能研究

陈树肖，郭金淮，王 晨，葛贵斌

（1.中国人民解放军国防大学联合作战学院，河北 石家庄 050084；2.中国人民解放军94201部队，山东 济南 250002；3.中国人民解放军93176部队，辽宁 大连 116023）

0 引言

1985年沈伟光提出信息战概念[1]，1991年海湾战争拉开了信息化战争序幕，随后，“网络中心战”“知识中心战”“分布式杀伤”“马赛克战”“决策中心战”等作战概念陆续提出。态势感知与信息融合、自主无人系统技术、人工智能等技术在军事领域的应用日益深入，推动信息化战争向更高 阶段发展[2-6]。

当前，信息化战争军事思想与军事技术进入快速发展阶段。军事信息服务系统是信息化战争的核心支撑要素，军事信息通常具有类型多样、重要信息优先服务的特点[7]。

军事信息服务系统数字化水平日益提升，离散时间排队模型是研究该系统的重要方法。作为数学与运筹学的重要分支，离散排队模型领域有大量研究成果：燕山大学马占友教授研究团队[8-10]，从数学角度出发，研究了离散排队模型；从应用角度出发，针对多优先级业务应用，郭金淮等人[11,12]对多优先级离散排队模型展开了相关研究，等待中断概率是主要研究内容；基于马尔可夫链，汪荣明[13]研究了两个吸收壁生死链的平均吸收时间。本文针对军事信息服务系统应用，基于军事信息服务系统特点，结合文献[11]动态优先级概念，并基于文献[13]对具体业务排队过程的分析，提出了扩展队列长度、虚拟状态空间、构造吸收壁等方法。此外，对各个优先级业务的性能进行了研究，具体性能包括阻塞概率、排队中断概率、服务成功概率、排队时间等，并得到了这些性能的显式数学表达式。

1 相关定义

为便于理解，对抢占型离散排队以及排队阻塞概率、排队中断概率、服务成功概率、排队时间等定义进行说明。

1.1 抢占型离散排队

在优先权服务中，高优先权顾客一旦到达，立即驱逐正在接受服务的低优先权顾客的服务，被称为抢占型优先权服务[10]。抢占型离散排队指高优先级业务到达，立即驱逐正在接受服务的低优先级业务或排在低优先级业务前面，低优先级业务按照优先级和到达时间重新排队。排队论中抢占型与抢占式含义相同，本文采用抢占型的说法。

1.2 排队阻塞概率

排队阻塞概率是指业务到达队列后，队列已满且队列中均为更高优先级业务或同优先级业务时，该业务未能进入队列的概率。

1.3 排队中断概率

排队中断事件指更高优先级业务到达时，该业务被挤出队列的事件，包括等待中断事件与服务中断事件。排队中断概率指业务进入队列未接受服务或未完成服务离开队列的概率。

1.4 服务成功概率

服务成功概率是指业务进入队列后，未发生排队中断事件时，该业务成功完成服务离开队列的概率。

1.5 排队时间

排队时间指从业务进入队列开始到业务离开队列所需的时间。离开队列可以是完成服务离开，也可以是被高优先级业务挤出队列。排队时间也就是指业务在队列中的时间，是等待时间或等待时间与服务时间之和。

2 系统模型

抢占型离散排队模型可描述如下。

2.1 业务到达

基于多优先级业务特点，业务优先级数量为r，r≥2。优先级i的业务记为Bi，i=1,2,…,r，i越小优先级越高。对于Bi来说，如果某时隙有高优先级业务到达，其到达概率为0；反之，则到达概率为pi，1>pi>0。

2.2 服务机制

采用单服务台，队长限制为N，其中N≥1，并采用抢占型离散排队。有业务接受服务时，每个时隙服务完成概率为μ，1>μ>0。

2.3 业务模型

考虑业务到达、服务完成以及业务被挤出队列时间，采用早到模型，即业务到达发生在时隙首端(n,n+)处，服务完成发生在时隙末端(n-,n)处[10]，低优先级业务被挤出队列时刻为相应高优先级业务到达时刻，即时隙首端(n,n+)。早到模型如图1所示。

图1 早到模型

以具体业务为研究对象，其到达前需要观察队列状态，因此观察时刻为时隙开始时，即时刻n。

2.4 参数关系

结合业务到达描述，每个时隙有业务到达的概率为：

排队系统达到稳态分布，需要满足业务到达概率小于服务完成概率的条件，即满足p<μ。

3 性能研究

根据系统模型，由于服务时间无记忆性，高优先级业务导致低优先级业务服务中断不影响服务效率。考虑军事信息服务系统业务排队具体过程，基于动态优先级与业务稳态队长分布，提出扩展队列长度、虚拟状态空间、构造吸收壁等方法，区分最高优先级业务与非最高优先级业务，并对排队阻塞概率、排队中断概率、服务成功概率、排队时间等性能进行研究。

3.1 最高优先级业务

根据抢占型离散排队工作机理，最高优先级业务不受其他业务影响，可独立分析。为便于研究其性能，下面对稳态队长分布进行分析。

时刻n最高优先级业务数为{Ln,n≥0}，对应状态空间是Ω={0,1,…,N}，其转移概率矩阵为：

基于最高优先级业务的状态转移概率矩阵、稳态队长分布，对其排队阻塞概率、排队中断概率、服务成功概率与排队时间进行研究。

（1）排队阻塞概率

排队阻塞概率为到达队列时，队长为N的概率。结合式（3）、式（4）得到：

（2）排队中断概率

最高优先级业务不会被抢占，排队中断概率为0，即：

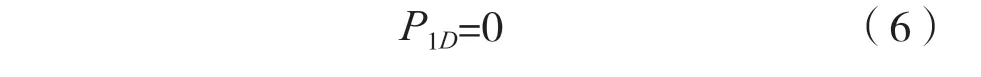
（3）服务成功概率

最高优先级业务不会被抢占，服务成功概率为1，即：

（4）排队时间

假设业务进入队列前队长为k，排队时间T1k为服务完k+1个业务所需时间。其中0≤k≤N-1。

根据系统模型，1个业务完成服务平均需要μ-1个时隙。因此T1k=(k+1)μ-1。

排队时间均值为：

3.2 非最高优先级业务

不失一般性，以Bi中某具体业务bi为研究对象，i=2,…,r。文献[11]动态优先级概念是针对多优先级抢占型离散排队提出的，仅考虑对排队性能有影响的业务，其本质是bi到达队列之前考虑B1,B2,…,Bi，到达队列之后考虑B1,B2,…,Bi-1。为方便描述，令BI表 示B1,B2,…,Bi，令BI-1表示B1,B2,…,Bi-1。令HI=(πI0,πI1,…,πIN)为BI的稳态分布，表示BI到达队列的概率，表示BI-1到达队列的概率。参考3.1部分，得到：

基于式（9）、式（10），对非最高优先级业务的排队阻塞概率、排队中断概率、服务成功概率与排队时间进行研究。

（1）排队阻塞概率

排队阻塞概率即bi到达队列时，BI队长为N的概率。

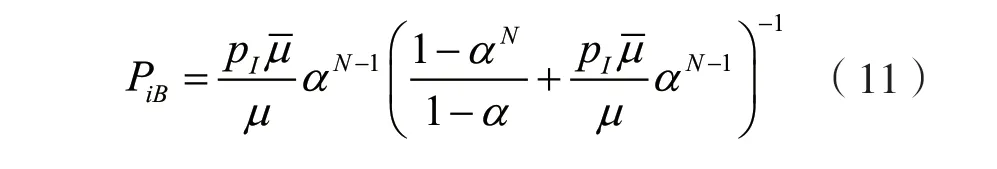
（2）排队中断概率

bi进入队列前，观察时刻记（0），BI业务稳态队长为k，0≤k≤N-1，k服从式（9）、式（10）概率分布。研究对象是前述k个BI业务、bi以及bi进入队列后到达的BI-1业务构成的队列，bi排在队列末尾。

bi进入队列时，队长为k+1。第1个时隙没有更高优先级业务到达，以概率μ完成1个业务服务。观察时刻（1），初始队长为k的概率为μ，初始队长为k+1的概率为1-μ。

为了研究排队中断概率、服务成功概率、排队时间等性能，下面提出扩展队列长度、虚拟状态空间、构造吸收壁等研究方法。

实际队列长度最大值为N，为便于研究，提出扩展队列长度研究方法，即在实际队列长度最大值的基础上加1，扩展后队列长度最大值为N+1。实际状态空间为Ω={0,1,…,N}，基于扩展队列长度，构造虚拟状态空间={0,1,…,N,N+1}。进一步地，根据虚拟状态空间构造吸收壁，结合系统模型，进入状态0和N+1，则状态不再发生变化，即状态0表示服务成功，状态N+1表示排队中断，状态0，N+1称为吸收壁。

基于虚拟状态空间，观察时刻（1）开始，具有双吸收壁的转移概率矩阵：

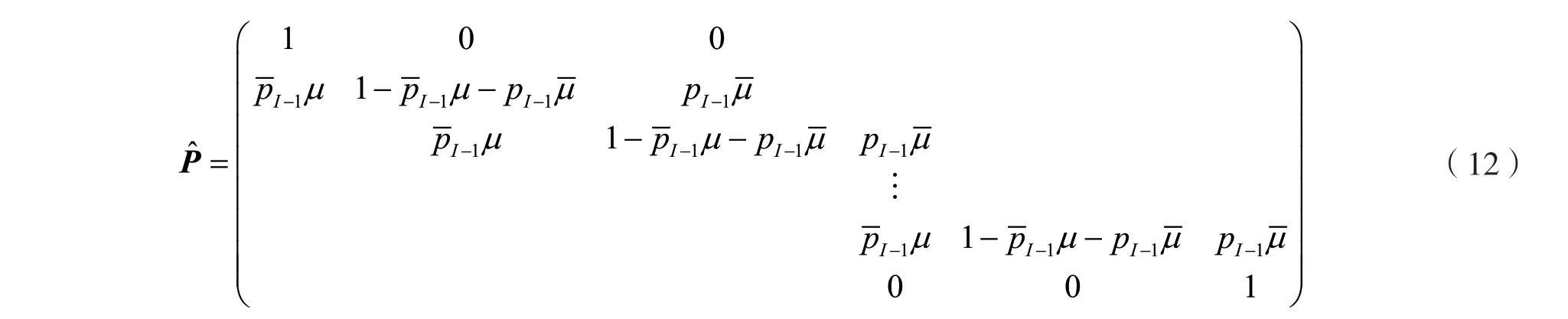
基于式（12），对文献[13]研究结果进行扩展，初始队长为x时，排队中断概率为：

式中：0≤x≤N+1，式（13）在空集上求和为零；F0=1；；i≥1。基于式（13），BI业务稳态队长为k时，bi排队中断概率为：

结合式（9）、式（10），得到bi排队中断概率：

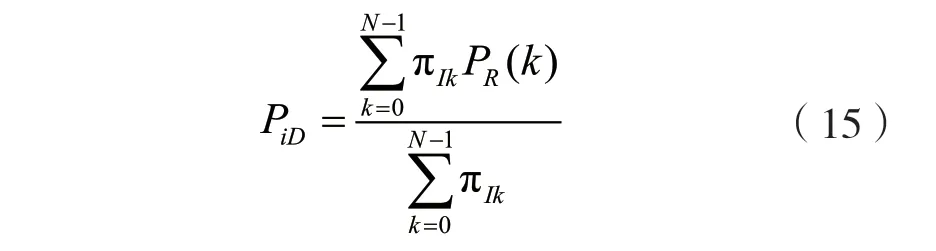
（3）服务成功概率

参考上述排队中断概率的分析过程，对服务成功概率进行研究。

初始队长为x时，服务成功概率为：

式中：0≤x≤N+1，式（16）在空集上求和为零；F0=1；Fi=βi；；i≥1。基于式（16），BI业务稳态队长为k时bi服务成功率为：

结合式（9）、式（10），得到bi服务成功概率：

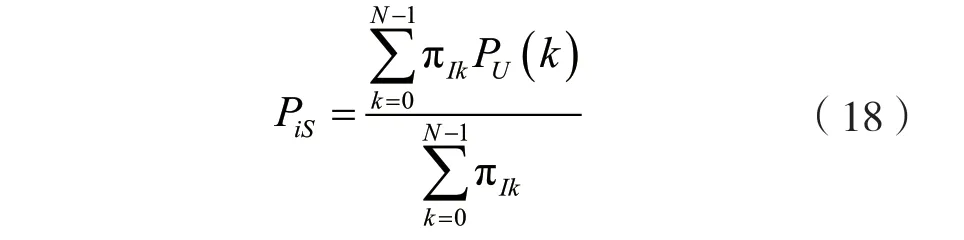
（4）排队时间

根据上述排队中断概率的分析，观察时刻（1），初始队长为k的概率为μ，初始队长为k+1的概率为1-μ。参考文献[13]研究结果，初始队长为x时，排队时间如式（19）所示。

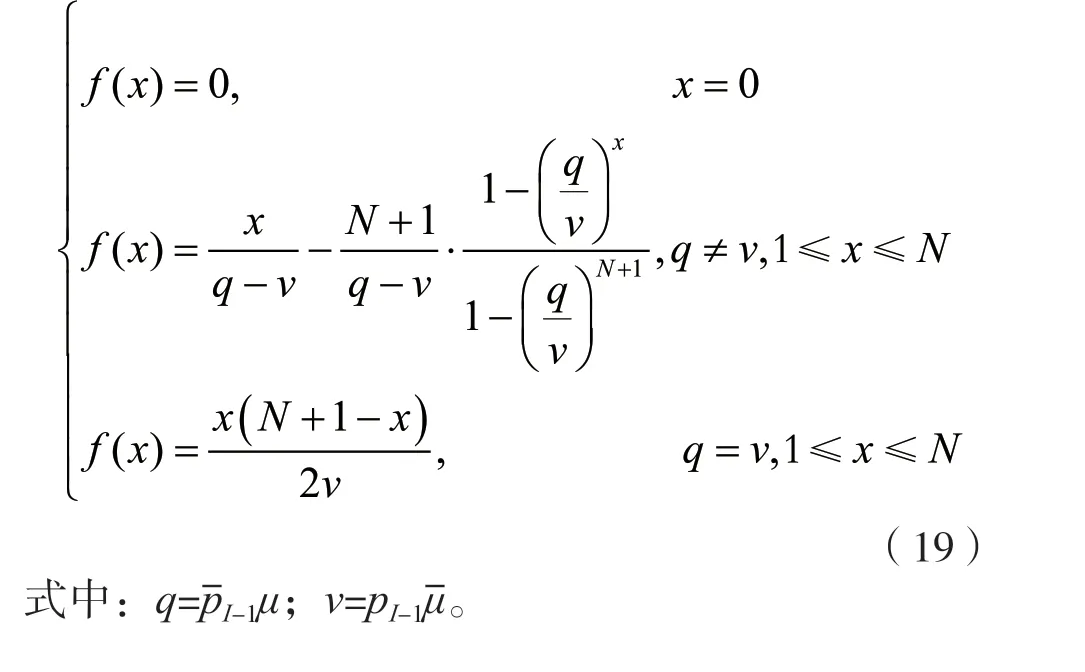
基于式（19），BI业务稳态队长为k时bi排队时间为：

结合式（9）、式（10），得到bi排队时间：

4 实例分析

影响排队性能的因素包括队长限制N、每个时隙服务完成概率μ、业务到达概率P等。下面通过实例，分析排队性能与相关因素的变化规律。

不失一般性，实例中变量为队长限制、每个时隙服务完成概率，常量为业务到达概率。业务优先级数量设为3，结合系统模型，假设优先级1，2，3业务的到达概率P=[p1,p2,p3]=[0.3,0.2,0.3]，以优先级3业务的排队性能为分析对象。

4.1 排队阻塞概率

队长限制N=3∶1∶10，每个时隙服务完成概率μ=0.7∶0.05∶0.8，排队阻塞概率变化趋势如图2所示。

图2 排队阻塞概率变化趋势

如图2所示，排队阻塞概率与每个时隙服务完成概率成反比关系，原因是每个时隙服务完成概率越高，业务到达时队列满的概率越低；排队阻塞概率与队长限制成反比关系，原因是队长限制值越大、队列容量越大，业务到达时队列满的概率越低。

4.2 排队中断概率

队长限制N=5∶1∶7，每个时隙服务完成概率μ=0.62∶0.02∶0.72，排队中断概率变化趋势如图3所示。

图3 排队中断概率变化趋势

如图3所示，排队中断概率与每个时隙服务完成概率成反比关系，原因是每个时隙服务完成概率越高，业务进入队列完成服务的概率越高、被高优先级业务挤出队列的概率越低；排队中断概率与队长限制成反比关系，原因是队长限制值越大，队列容量越大，被更高优先级业务挤出队列的概率 越低。

4.3 服务成功概率

队长限制N=5∶1∶7，每个时隙服务完成概率μ=0.62∶0.02∶0.72，服务成功概率变化趋势如图4所示。

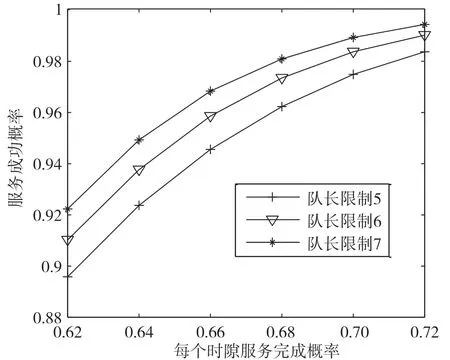
图4 服务成功概率变化趋势

如图4所示，服务成功概率与每个时隙服务完成概率成正比关系，原因是每个时隙服务完成概率越高、被更高优先级业务挤出队列的概率越低，服务成功概率越高；服务成功概率与队长限制成正比关系，原因是队长限制值越大，队列容量越大，被更高优先级业务挤出队列的概率越低，完成服务离开队列的概率越高。

4.4 排队时间

队长限制N=5∶1∶7，每个时隙服务完成概率μ=0.62∶0.02∶0.72，排队时间变化趋势如图5所示。

图5 排队时间变化趋势

如图5所示，排队时间与每个时隙服务完成概率成反比关系，原因是每个时隙服务完成概率越高，业务以更高概率、更短时间完成服务；排队时间与队长限制成正比关系，原因是队长越长，业务服务成功或被高优先级业务挤出队列所需时间越长，即排队时间越长。

5 结语

本文针对军事信息服务系统业务类型多样、重要业务优先服务的特点，建立了多优先级抢占型离散排队模型。文中分析了系统业务的具体排队过程，采用扩展队列长度、虚拟状态空间、构造吸收壁等方法，区分业务优先级，对排队阻塞概率、排队中断概率、服务成功概率、排队时间等性能进行研究，并得到其显式数学表达式。本文研究结果对军事信息服务系统的设计、维护、管理与使用具有参考价值，还可应用于其他具有类似特征的信息服务系统。