一种动态起伏的海表面建模方法

王兆旗 范国章* 丁梁波 张 威 叶月明 王宗仁

(①中国石油杭州地质研究院，杭州 310023； ②上海勘察设计研究院(集团)有限公司)

0 引言

受风速、潮汐、重力等环境因素影响，真实的海面通常是起伏不定且随时间动态变化的。地震波在海水中传播时，遇到起伏海面会发生特殊的散射和反射，对地震数据产生影响[1]。同时，起伏海面改变了鬼波的传播路径，导致鬼波延迟时间发生变化。因此，动态的起伏海表面会导致鬼波参数估算不准确，无法获得理想的鬼波压制效果[2]。

近年来，围绕起伏海平面对地震数据的影响，相关学者做了大量的研究。Jovanovich等[3]早在1983年就定性分析了不同高度起伏海面对鬼波的影响； Laws等[4]对观测得到的时移地震成像结果进行分析，认为即使高为2m的相对平静的海面也会对时移地震结果造成影响； Kragh等[5]研究了由于起伏粗糙海面引起的统计反褶积的变化； Orji等[6]、Cecconello等[7]及Blacquière等[8]基于克希霍夫数值模拟方法计算了海面的散射波场； Egorov等[9]采用克希霍夫近似法数值模拟起伏海面，分析了震源较深的情况下起伏海面对地震成像的影响。

中国学者也在该领域开展了广泛而深入的研究。张威等[10]利用最小平方成像条件对海水表面进行成像以校正检波器实际沉放深度，并利用校正后的深度进行去鬼波处理； 李志鹏等[11]利用蒙特卡洛法对粗糙海面进行建模，并求取海面反射系数； 孟祥羽等[12-13]在PM(Pierson-Moscowitz)海浪谱的基础上利用中国的海浪谱建立起伏海面模型，研究中国海域内起伏海面条件下的地震反射响应。

但这些文献均未考虑海面的动态变化及由此带来的影响。在前人研究的基础上，本文提出了一种基于动态起伏海表面的建模方法。首先，考虑到起伏海面的运动学特性、模拟检波器鬼波以及非脉冲源的震源鬼波，采用将几个动态海面“冻结”快照的计算结果组合成一个有效的静态粗糙海面来实现； 然后，采用克希霍夫近似法，利用PM海浪谱计算模型建立海面起伏模型，以此研究动态起伏海面条件下的地震波响应特征。

1 方法原理

1.1 动态起伏海表面下鬼波建模方法

1.1.1 震源端鬼波建模

对于震源端鬼波，从一个气枪阵列产生的脉冲震源开始，动态起伏的海面可以近似为一个等效的静态粗糙海面。这是因为震源信号在特定地点和特定时间只从海表面反射一次(在粗糙海面的情况下忽略可能的双重反射)。这一地点和这一时刻海面的形状决定了鬼波的来源(图1)。如图所示，等效起伏海面由t1、t2、…、tn时刻所记录的海表面合并组成，其中n为时间采样个数。

对于每个单炮记录，由于不同的炮点位置和不同的放炮时间，等效静态海面也会相应地变化，所以每个单炮记录都需要重新进行海平面计算。

1.1.2 检波器端鬼波建模

对于检波端鬼波而言，在地震波记录过程中，海面的形状可能发生显著的变化。为对一个单炮激发过程中海面的动态特性建模(图2)，首先，把采样长度分成n份，每一份时间为Δt； 然后，按照所有的时间间隔Δt进行重复建模，在建模过程中，每个记录对应一个不同的静态起伏海面； 最后，依次从建模记录中选择与时间间隔相对应的结果，获得最终的单个单炮记录，即按照时间间隔Δt、2Δt、…、nΔt分别对应记录1、2、…、n(图2中红色大括号标注部分)重新合成新的单炮记录。

1.2 PM海浪谱

起伏海面具有随机性，可用Pierson等[14]讨论的PM海浪谱方法建模。PM用来为不同的海洋状态创建海面形状，它是一种经长期观测、具有充分依据的经验谱，准确性相对较高。用这种方法得到的海表面展示了不同的海况。标准波高(SWH)见表1[15]，其中1～9级分别称为无浪、微浪、小浪、中浪、大浪、巨浪、狂浪、狂涛、怒涛。图3是与海况等级1～9相关联的海面模型。

图1 等效动态起伏海表面示意图

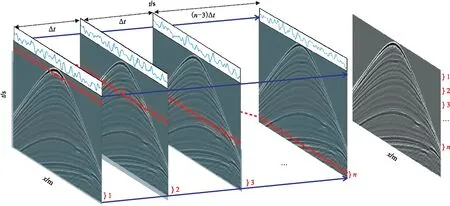
图2 检波端鬼波情况下的等效动态起伏海表面生成示意图t代表采样时间； x表示炮检距

利用Pierson和Moskowitz提出的方法[14]为不同海洋形态创建海表面模型

(1)

式中：S(ω)表示海面模型函数，其中ω是海面的起伏频率；u是海平面上方19.5m处的风速；α=0.0081；β=0.74；g是重力加速度。根据海面起伏频率ω与波数k的关系

ω2(k)=gk

(2)

可把海浪谱写成波数域的形式，将波数域的海浪谱乘以一组高斯分布的随机复数，然后对其进行傅里叶逆变换，便得到不同海况下的随机起伏海面模型。

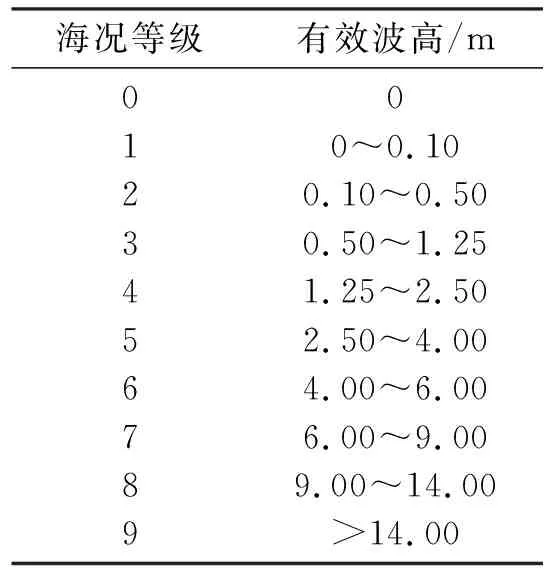
表1 不同海况等级的波高

图3 与海况等级相关联的海面(a)等级1； (b)等级2； (c)等级3； (d)等级4； (e)等级5； (f)等级6； (g)等级7； (h)等级8； (i)等级9

1.3 克希霍夫近似法

为了在地震波场建模中引入动态起伏海面，首先需要构建一个动态海面模型，以真实的波浪形状和运动学特征描述海面形状随时间变化的函数。为便于计算，从“冻结”在某一时刻的静态粗糙海面的假设情况开始。如图4所示，A代表“冻结”在某一时刻的海表面，平均水位线为z0。在地震波场模拟中，起伏海面边界与起伏地表边界往往存在较大差异，起伏地表高程变化较大，而起伏海面尺度较小。Laws等[4]基于PM海浪谱采用克希霍夫方法进行起伏海面正演模拟。Robertsson[16-17]等对比分析了克希霍夫近似法、谱元法和有限差分法等数值模拟方法的优缺点，认为克希霍夫近似法结果与其他方法的差异较小，但是效率更高。在频率域，利用克希霍夫近似法模拟海表面A(图4)的散射波下行波场P+(r)，可表示为

(3)

(4)

(5)

式中：r是炮点到检波点的矢量；r1和r2分别代表炮点到海表面和海表面到接收点的矢量；G(r2)代表自由空间的格林函数；P-(r1)代表上行反射波场； ∂P-(r1)表示P-(r1)的一阶求导； ∂n表示在x、y、z方向的一阶求导； i为虚数单位；B代表炮点的振幅； 水/空气界面的反射系数取为-1。

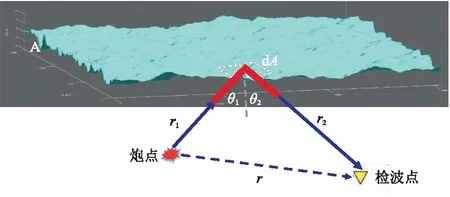
图4 观测系统示意图

2 模型测算

2.1 随机起伏海面模型

图5是有效波高为2.5～4.0m海况下的随机起伏海面二维模型，以此为基础，建立Marmousi速度模型创建合成数据(图6)，在该模型上方增加了基于图5所示起伏海表面的水层以模拟实际海洋情况。模拟参数为：道间距7.5m,道数400,采样点数512,采样率4ms； 拖缆和震源分别位于海表面以下20m和30m处，主频为30Hz。模型采用PML的吸收边界条件。

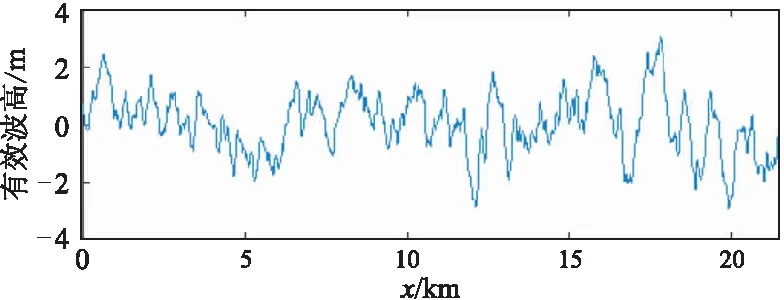
图5 有效波高为2.5～4.0m海况下的随机起伏海面模型

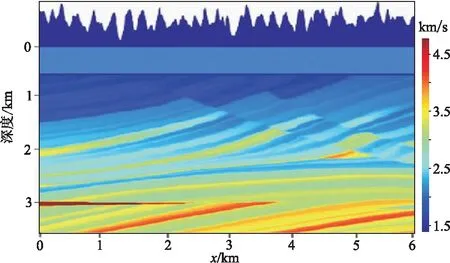
图6 基于起伏海表面的Marmousi速度模型

2.2 震源端鬼波模拟记录

图7a为“动态”起伏海面的正演模拟记录，以一维等效起伏海面为计算区域的上边界，拖缆位于海面下20m处。从图7b的局部放大图可见，由于不同炮点对应不同的海表面，地震记录中鬼波同相轴存在明显的“抖动”现象。这种“抖动”在所有时刻均存在，且与海面的动态变化有关。

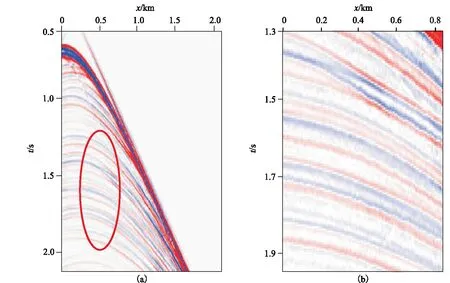
图7 包含震源端鬼波的共检波点道集(a)及其局部(左图红色圆圈)放大图(b)

图8a、图8b分别为“静态”和“动态”起伏海表面模拟生成的共检波点道集； 图8c为图8a和图8b的差值。从图8可以看到动态起伏海面使得地震记录产生了较多的噪声。图9是图8道集分别对应的频谱，由图可见，受动态起伏海面的影响，陷频缺口变得模糊。图10和图11分别是不同海况等级(2、5、8)生成的共检波点道集及其对应频谱，由图可知，随着海况等级的提高，频谱上的陷频缺口变得越来越模糊，给鬼波压制带来了更严峻挑战。

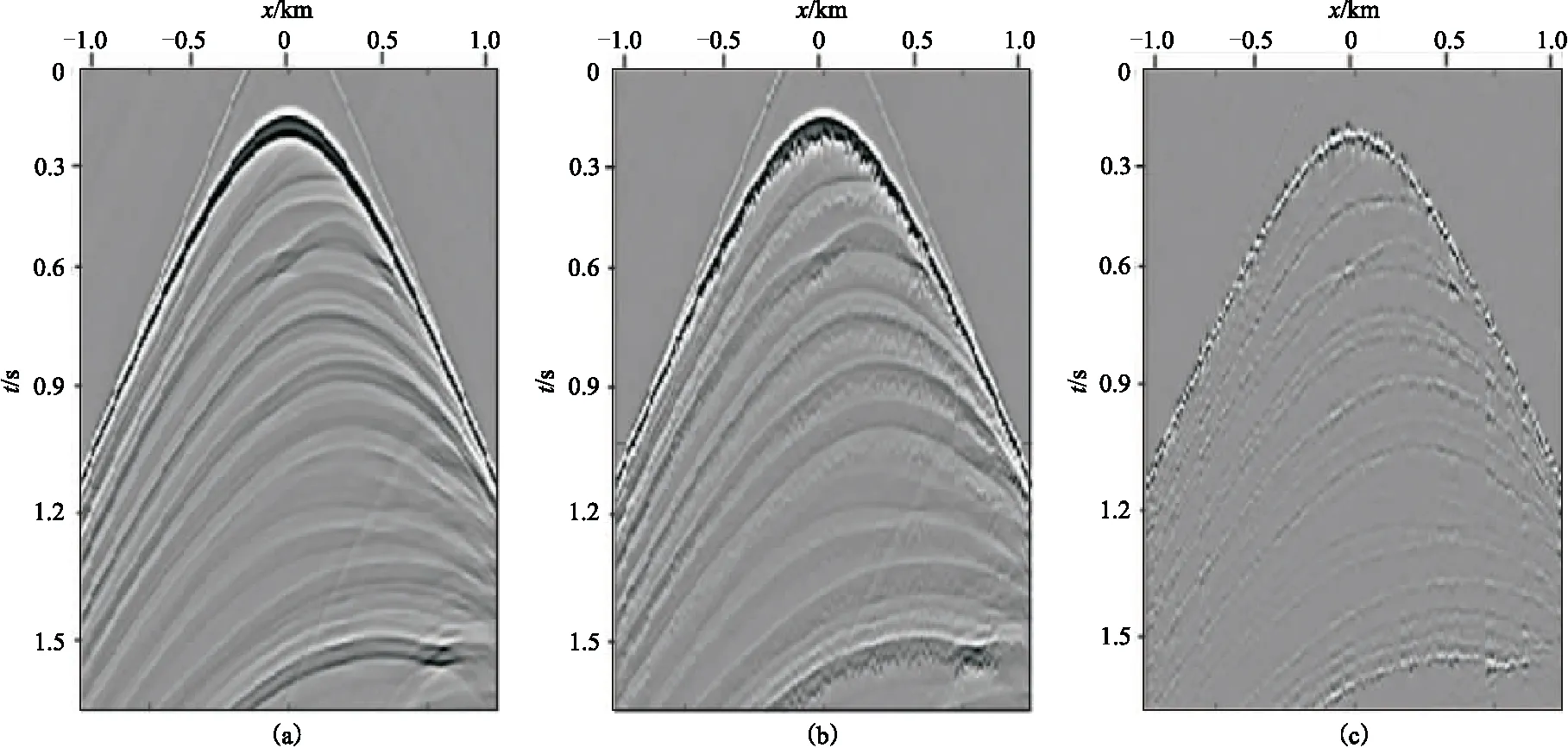
图8 “静态”(a)、“动态”(b)起伏海表面模拟生成的共检波点道集及道集差(c)

图9 “静态”(a)、“动态”(b)起伏海表面模拟生成的共检波点道集频率及频谱差(c)

2.3 检波器端鬼波模拟记录

对接收器鬼波进行建模的结果如图12和图13所示。其中，图12a是“静态”起伏海表面模拟生成的共炮点道集，图12b为“动态”起伏海表面模拟生成的共炮点道集，图12c为图12a和图12b的差值，表明了相对“静态”起伏海表面，动态起伏海面产生了更多的“噪声”； 图13a为海况3情形下的建模情况，图13b为海况6情形下的建模情况，可见随着海况等级的提高，频谱的陷频缺口变得越来越模糊，给后期的鬼波压制增加了难度。

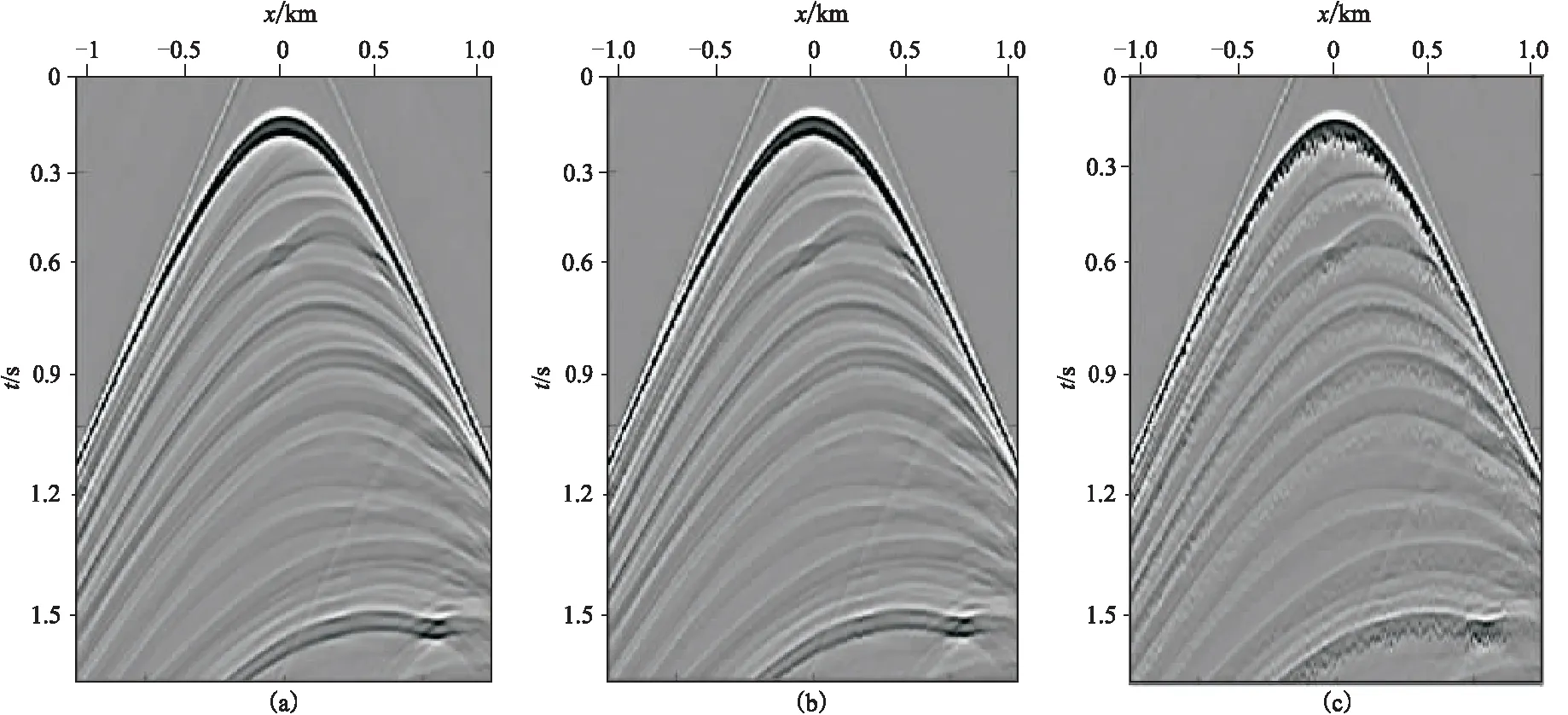
图10 海况等级为2(a)、5(b)、8(c)时的“动态”海表面生成的共检波点道集

图12 “静态”(a)、“动态”(b)起伏海表面模拟生成的共炮点道集及道集差(c)

图13 海况等级为3(a)和6(b)时的动态海表面生成的共炮点道集频谱

3 结束语

由于受到风、重力和潮汐等环境因素影响，真实的海水一直处于运动状态，海面也是起伏的，因此对地震数据的鬼波压制造成影响。采用PM海浪谱计算模型建立随时间变化的“动态”海面起伏模型，通过对Marmousi模型的数值模拟，得到以下认识：

(1)“动态”起伏的海面影响鬼波传播距离，导致鬼波与一次反射波之间的时间间隔发生变化，出现鬼波同相轴的“抖动”现象；

(2)对于“动态”海面，应采用不同的方法分别计算震源端鬼波和检波器鬼波，每个震源的“动态”海面可采用一个有效的“静态”海面来代替，并采用多次“静态”模型来模拟“动态”情况；

(3)随着有效波高的增加，频谱的陷频缺口变得越来越模糊，进而影响鬼波的压制效果。

感谢荷兰代尔夫特大学Eric Verschuur教授、Jan-Willem和Cao Junhai博士提供的热情帮助。