基于RANS湍流模型的梯形柱气动特性研究*
2022-06-11田洪森程文明王书标
田洪森 程文明 杜 润 王书标
1西南交通大学机械工程学院 成都 610031 2轨道交通运维技术与装备四川省重点实验室 成都 610031
0 引言
钝体绕流是工程中的热点问题,柱体结构在风荷载的作用下,其安全性和稳定性问题一直受到持续关注。工程应用中的结构绕流多为高雷诺数场景,此时流体的湍动能较大,受流体湍流特性的影响,结构的绕流特性愈发的复杂,故对高雷诺数下柱体结构绕流特性的研究具有极高的工程意义。
国内外学者对钝体绕流进行了大量的研究。Lyn D A等[1]基于FLDV实验测试了雷诺数为2.2×104时方柱的流场,得出方柱尾缘的速度分布规律以及涡的分布与大小。张伟等[2]采用粒子图像测速仪(PIV)和数值模拟对方柱绕流进行了研究,得出数值模拟计算结果与实验数据吻合较好。Norberg C[3]利用风洞实验对2种风攻角下的矩形柱进行研究,得出了斯托罗哈数St随宽高比R的变化规律。沈国辉等[4,5]通过数值模拟对圆柱绕流进行研究,得到的数据与实验结果相符。杜晓庆等[6]研究了不同形状下类方柱的气动性能和流场特性,重点分析了凸边圆角柱的气动性能随边部曲率半径的变化规律,并通过分析流场揭示了平面形状修正对类方柱气动性能影响的作用机理。梁思超等[7-12]采用不同的方法对高雷诺数下矩形柱的气动特性进行了研究,并于相关的风洞试验对比,得出数值上与参考值相差较小。Kahawita R等[13-15]通过对梯形结构的数值模拟,研究发现与较小的梯形底宽相比,梯形的高度是影响Strouhal数值的主要因素。
综上所述,无论是风洞实验还是数值仿真,钝体绕流研究一般多集中在矩形柱和圆柱,对梯形柱的研究却很少,且研究多为横置结构,而竖立梯形在实际中却应用较多,如桥梁和起重机等工程结构。基于此,本文以高度为1 m的竖立梯形柱为研究对象,通过流体计算软件Fluent开展绕流特性研究,总结不同梯形截面结构特征参数下的气动力参数变化规律。
1 数值计算方法
1.1 控制方程
根据工程中的实际工况,文中采用的是高雷诺数下的湍流模型,基于流体计算软件Fluent,空气视为不可压缩流体,选用 Realizablek-ε湍流模型。Realizablek-ε湍流模型对于流动分离与二次流动的模拟相较于RNGk-ε模型与标准k-ε模型更为准确且易收敛。Realizablek-ε湍流模型的方程为
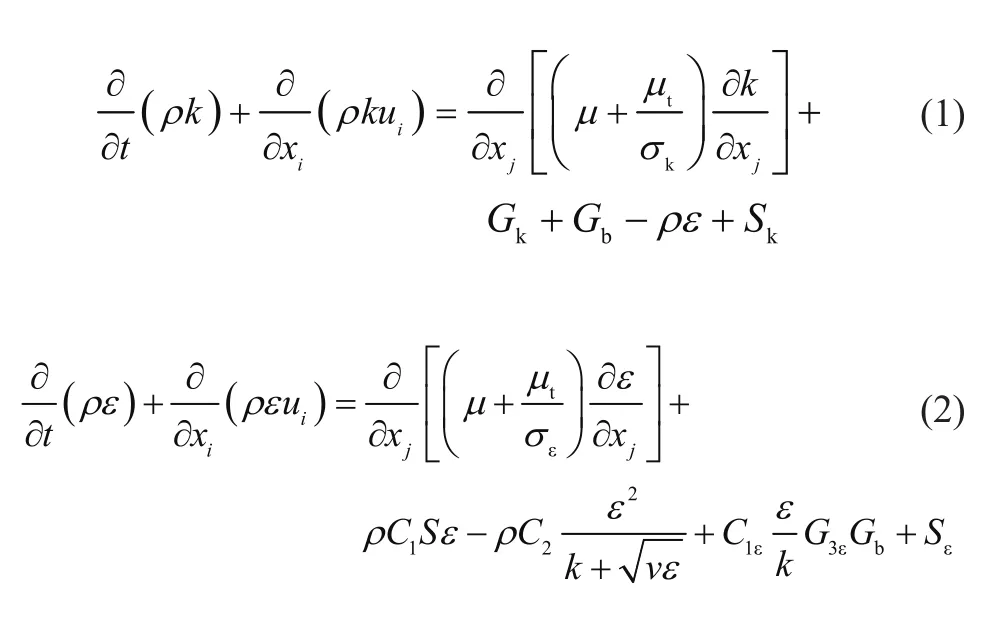
1.2 数学模型
流域中梯形柱结构布置如图1所示,梯形柱处于恒定的自由流场中。梯形截面的下底边长为B,上底边长为B+2Δb,梯形柱高度为H,定义梯形柱的偏角为θ(即为来流方向与梯形柱迎风面的夹角),其中tanθ=H/Δb,θ=arctan(H/Δb),宽高比R=B/H。上游流域长为10H,下游流域为20H,梯形柱到上下边界的距离各为10H。

图1 梯形柱绕流计算域和边界条件
入口边界条件采用均匀来流速度边界条件,来流速度U=10 m/s,出口采用零压力出口条件,上下边界采用对称面,梯形柱壁面采用无滑移壁面边界条件,来流湍流强度为5%。
在计算方法的选取上,Simplec算法在四边形网格上比Simplec算法更准确、稳定,因此本文选用Simplec算法来求解压力速度耦合方程,采用Piso算法处理瞬态问题,对流插值采用Quick格式,压力插值采用二阶格式。
梯形柱采用O形网格划分,对梯形柱周围壁面进行边界层网格加密,网格示意图如图2所示。
图2 梯形柱网格划分及局部放大图
1.3 网格无关性验证
对梯形截面分析前需进行网格无关性分析,网格精度不仅影响仿真计算精度,还影响计算的效率。以宽高比为R=1的方柱为例,研究其在雷诺数Re=6.8×105下的绕流情况,通过选取3套不同的网格来验证网格的无关性,3套网格的差异在于第一层网格高度y0/H和延展因子α的不同,模拟结果如表1所示。
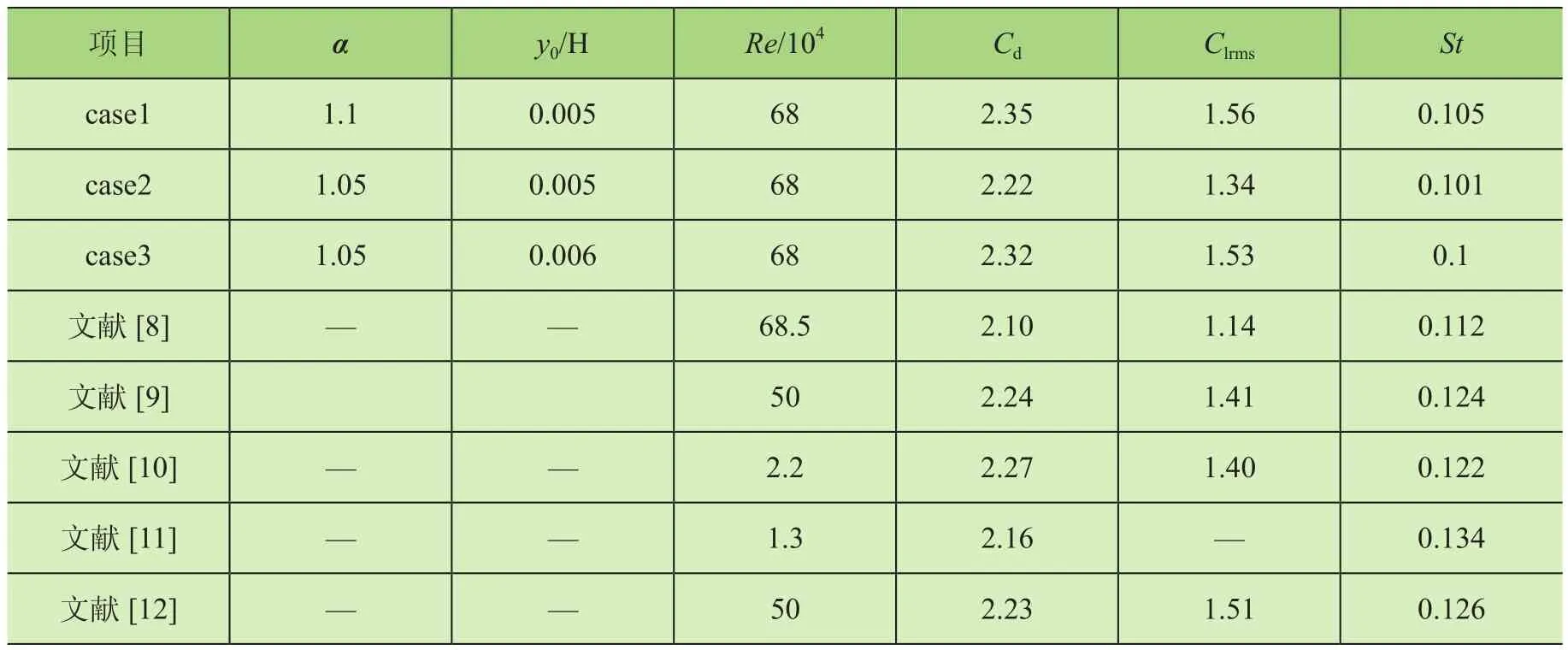
表1 不同网格计算结果及对比
根据文献[8-12]的研究结果,对于高雷诺数下的方柱绕流,气动参数随雷诺数的变化很小。通过不同网格条件下的计算结果与文献的对比,算例仿真得到的阻力系数Cd、升力系数均方根Clrms和斯托罗哈数St与文献的仿真结果吻合都较好。综合考虑计算开销并保证计算精度,后续仿真皆采用case2的网格参数对梯形柱进行网格划分。
2 模拟结果分析
本文仿真采用Realizablek-ε湍流模型,对高雷诺数(Re=6.8×105)下不同截面大小的梯形柱进行仿真计算和结果分析,柱体截面的变化通过改变梯形柱的宽高比R和偏角θ来实现,其中宽高比R的变化范围为0.5、0.6、0.7、0.8、0.9、1.0,偏角θ的变化范围为θ1=arctan(H/0.1),θ1=arctan(H/0.2),θ1=arctan(H/0.3),共计18种不同梯形截面。本文主要讨论的气动参数包括阻力系数Cd、升力系数均方根Clrms和斯托罗哈数St等,并将其结果与矩形柱的气动参数进行对比分析。
2.1 梯形柱绕流分析
图3为宽高比R=1.0、偏角为θ1和θ3时梯形柱的表面平均压力系数分布,由图可知,柱体前壁面的压力系数为正,其余各壁面的压力系数为负。将数值模拟结果与同宽高比下的矩形柱相比可知,梯形柱压力系数值不在中间平面达到最大值,而在中间偏上的平面处达到最大值,且梯形柱偏角越小,最大值所处平面越往上。在上壁面(BC段)、后壁面(CD段)和下壁面(DA段)梯形柱的压力系数值高于矩形柱,且偏角越小,压力系数越高。
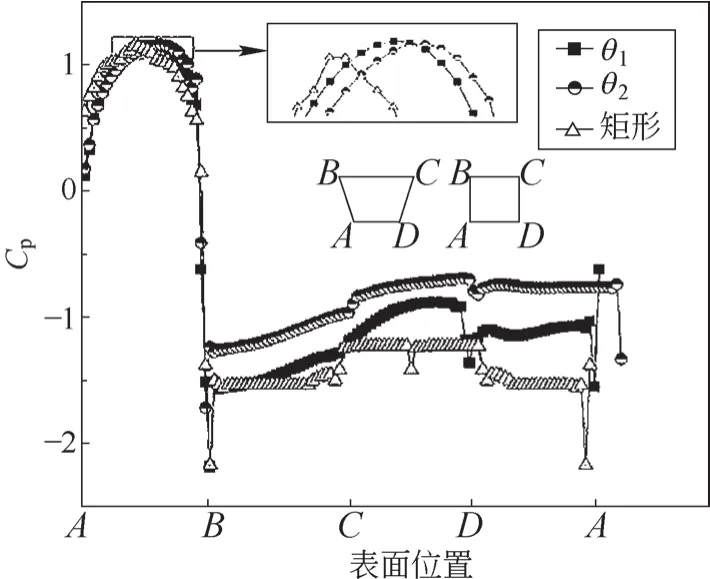
图3 梯形柱表面平均压力系数分布
2.2 梯形柱的气动参数分析
不同宽高比和不同偏角梯形柱的气动参数随着宽高比和偏角的变化趋势如图3所示。
图4a为阻力系数与偏角和宽高比的变化关系图,由图可知,当梯形柱偏角不变时,梯形柱阻力系数在宽高比R=0.5时达到最大,随着宽高比的增大,阻力系数逐渐减小;当梯形柱的宽高比不变时,阻力系数在偏角θ=θ1时达到最大,随着偏角的减小而减小。
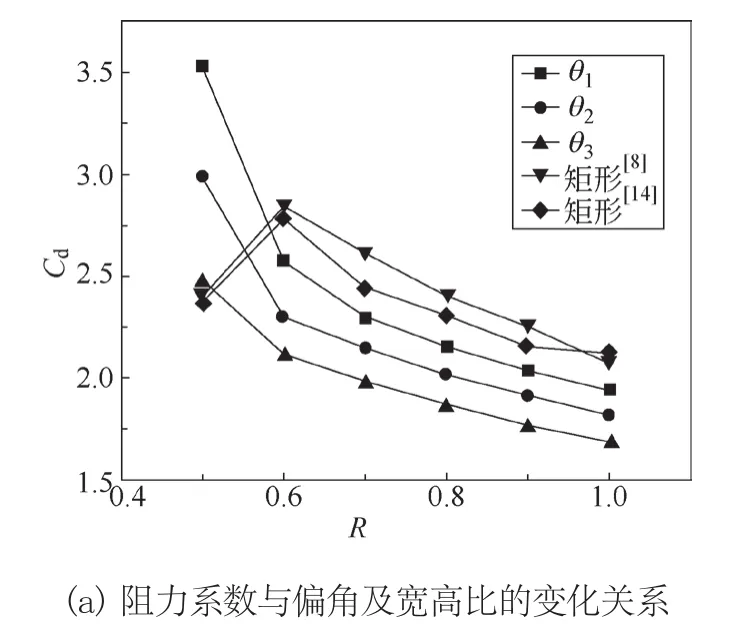

图4 不同梯形截面下的气动力参数变化趋势
与文献[8,14]矩形柱的阻力系数变化趋势相比,由于受偏角的影响,梯形柱的阻力系数曲线没有像矩形柱阻力系数曲线一样出现极大值。当宽高比R=0.5时,梯形柱的阻力系数大于矩形柱的阻力系数,当宽高比R=0.6~1.0时,梯形柱的阻力系数小于矩形柱的阻力系数。
图4b为升力系数均方根与偏角和宽高比的变化关系图,由图可知,当梯形柱的偏角不变时,升力系数均方根在宽高比R=0.5时达到最大,随着宽高比的增加,升力系数均方根逐渐减小。当梯形柱的宽高比不变时,升力系数均方根在偏角θ=θ1时达到最大,且随着偏角的减小而减小。与文献[8]矩形柱的升力系数均方根相比,由于受偏角的影响,在宽高比R=0.6~1时,在高雷诺数条件下同一宽高比的梯形柱和矩形柱,梯形柱的升力系数均方根更小。
图4c为斯托罗哈数与偏角和宽高比的变化关系图,由图可知,当宽高比不变时,偏角越大,斯托罗哈数越大。当偏角不变时, 斯托罗哈数在宽高比R=0.6时出现极大值,在宽高比R<0.6时逐渐增大,在宽高比R>0.6时逐渐减小。当宽高比R=0.5~0.6的范围时,由于梯形柱宽度的增加,分离流在上下迎风面形成部分再附,涡脱频率发生变化,导致斯托罗哈数增加。
2.3 梯形柱的流场特性分析
图 5 为宽高比R=0.5、0.6、1.0 和偏角θ=θ1、θ3下 ,升力达到最大时的涡量云图。由图可知,流体在梯形柱上下迎风面的角点处产生分离,在结构的下游再附。随着流体的流动,涡的能量逐渐消解,而结构尾涡距离的远近会导致结构背风面的压力变化,从而影响柱体的阻力值。当R=0.5、θ=θ1时,结构尾部产生2列涡,尾涡到背风面的距离最近,因此在背风面产生的负压最大,结构前后的压差最大,阻力系数最大。当R=0.6、θ=θ1时,结构尾部产生单列涡,尾涡到背风面的距离变大,因此产生的负压降低,前后压差变小,阻力系数降低。当偏角不变时,随着宽高比的增加,尾涡由2列变为1列,且尾涡到背风面的距离变长,从而阻力系数变小。当R=0.5、θ=θ3时,结构尾部产生2列涡,相比于图5a,尾涡到背风面的距离变长,导致阻力系数变小。当宽高比不变时,结构尾部产生的尾涡形式不发生变化,随着偏角的减小,结构尾涡到背风面的距离增大,导致阻力系数减小。
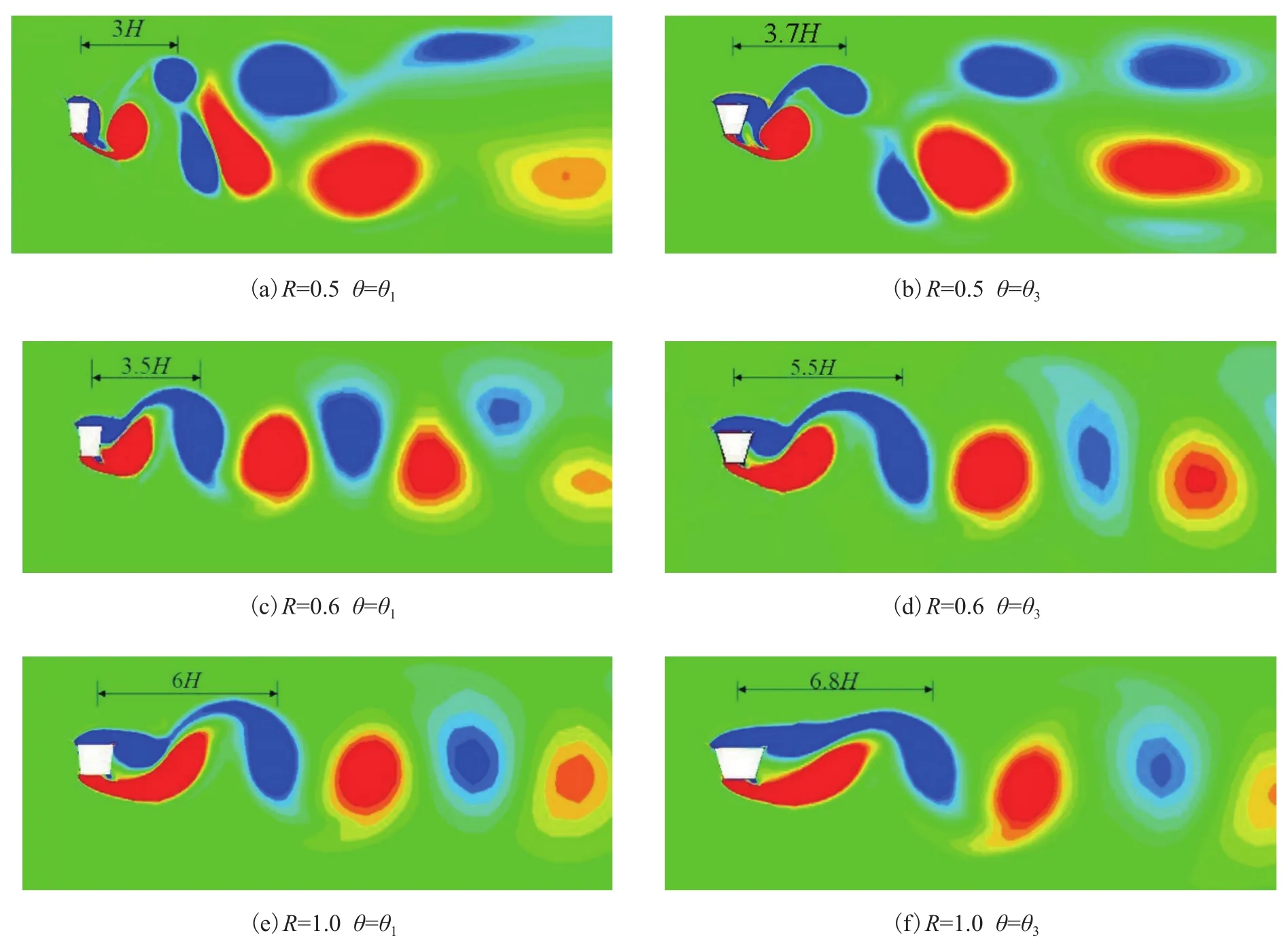
图5 升力最大时不同截面梯形的尾流涡量图
图 6 为宽高比R=0.5、0.6、1.0 和偏角θ=θ1、θ3下梯形柱的平均压力云图。流体在柱体角点分离,由于分离流具有更高的流速,流体流速的增加会使其压强降低,因此分离流会抽吸结构背风面的空气,使得背风面产生负压。由图可知,梯形柱前迎风面的压力为正,上下迎风面和背风面的压力为负。由图6a可知,当梯形柱的偏角最大时,在结构背风面的负压最大,此时柱体前后形成的压差最大,因而阻力系数最大;相比图6c、图6e,当偏角不变时,随着宽高比的增加,结构背风面的负压逐渐减小,柱体前后压差减小,故阻力系数逐渐减小。相比图6b,当宽高比不变时,偏角变小,结构背风面的负压减小,柱体前后的压差减小,阻力系数减小。
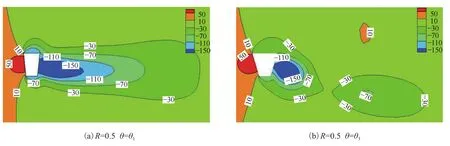
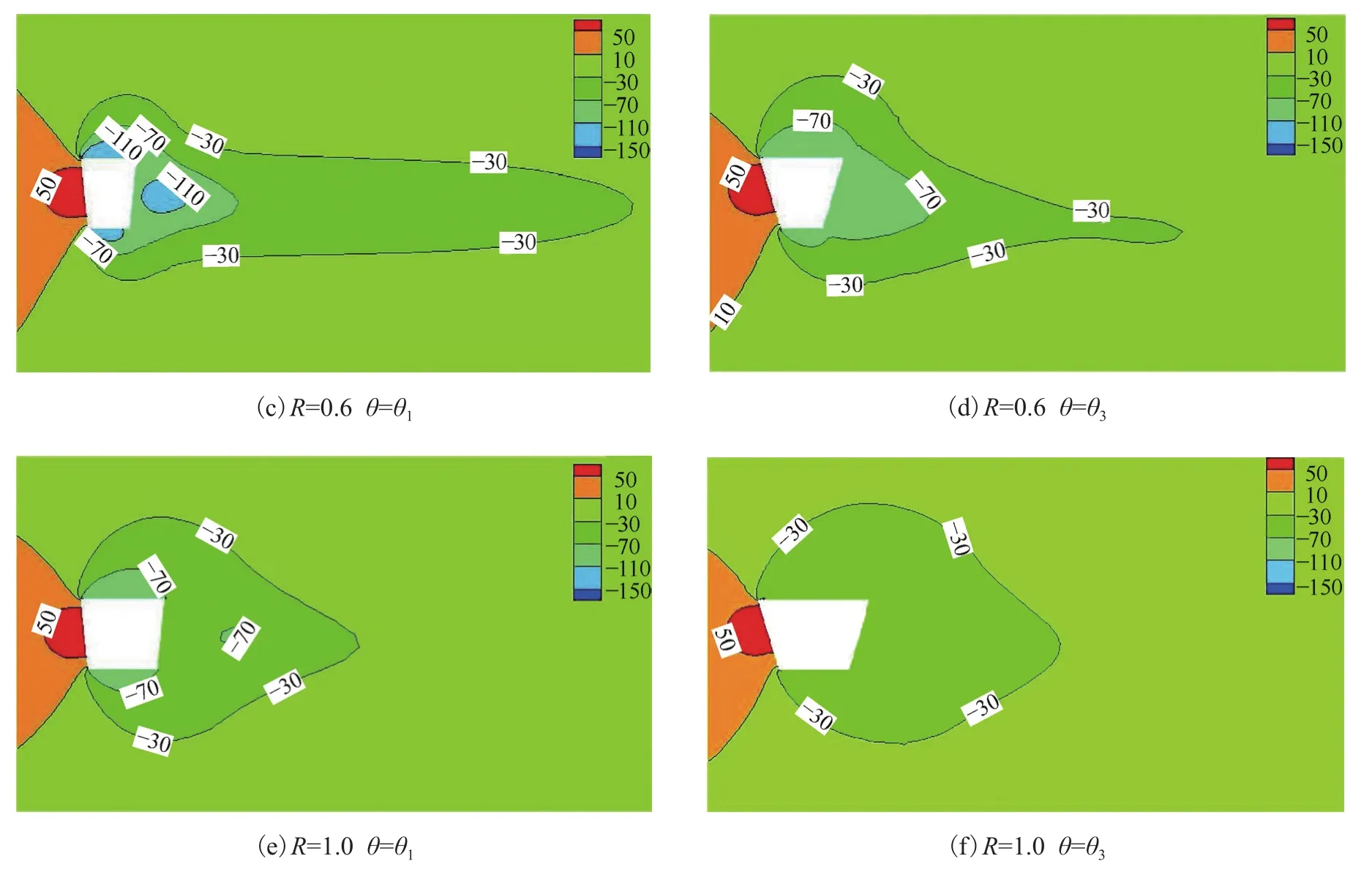
图6 不同梯形截面尺寸下的平均压力云图
3 结论
1)受偏角的影响,梯形柱前迎风面压力系数最大值在柱体中偏上处,且偏角越小,压力系数最大值越偏上。当宽高比R=0.5时,梯形柱的阻力系数大于矩形柱的阻力系数,此时矩形柱优于梯形柱;当宽高比R>0.5时,梯形柱的阻力系数小于矩形柱的阻力系数,此时梯形柱优于矩形柱。
2)当偏角不变时,随着宽高比的增加,阻力系数、升力系数均方根逐渐减小,斯托罗哈数先增加后减小;当宽高比不变时,随着偏角的变小,阻力系数、升力系数均方根、斯托罗哈数逐渐减小。
3)从流场特征角度说明了当偏角不变时,随着宽高比的增加,阻力系数呈下降趋势;当宽高比不变时,随着偏角的增大,阻力系数呈上升趋势。
