各向异性地层定向射孔压裂裂缝发展形态研究
2022-06-10刘红磊仲冠宇
刘红磊,仲冠宇
(1.页岩油气富集机理与有效开发国家重点实验室,北京 100101;2.中国石化石油工程技术研究院,北京 100101)
低渗透储层基质渗透率及孔隙度极低,需通过水力压裂技术才可以获得工业油气流。利用定向射孔压裂技术,可以使射孔角度与水平主应力方向呈一定的夹角,进而诱导裂缝转向,产生“S”形或“X”形裂缝,从而增加泄油面积,提高单井产能。目前,该技术已成功应用于低渗透储层的开发[1-3]。
定向射孔压裂条件下裂缝的发展形态对单井增产效果有着重要影响。室内实验[4-7]可以定性分析定向射孔压裂下裂缝的扩展机理及影响因素,但存在的尺度效应等问题造成了研究结果难以直接用于现场。有学者通过有限元法[8-9]、边界元法[10-13]等分析了水力压裂裂缝的发展形态,但这些研究均将岩石简化为各向同性的弹性均质体,这与煤岩、页岩等层理、裂隙发育的岩石严重不符。在前人研究的基础之上,依据各向异性弹性力学基本原理,基于边界元法建立了各向异性地层中定向射孔压裂条件下裂缝发展形态的计算模形,研究了裂缝形态及影响因素,从而为定向射孔压裂技术的研究与应用提供了理论依据。
1 定向射孔压裂条件下裂缝扩展模形的理论基础
1.1 基本方程
煤岩、页岩等岩石节理、裂隙发育,这类岩石具有不同程度的弹性各向异性。为真实地模拟裂缝扩展过程,将岩石简化为各向异性弹性体,则作用于岩石的应力应满足平衡方程:

式中:σij,j为应力分量对j坐标的偏导数;fi为体力分量,Pa;i表示体力分量的方向及应力分量所在坐标面的外法线方向,沿xi方向,称为面元指标;j表示应力分量的分解方向,沿xj方向,称为方向指标。
当i=j时,应力分量垂直于面元方向,称为正应力,当i≠j时,应力分量作用在面元平面内,称为剪应力。岩石的应力和应变满足本构方程:

式中:H为柔度矩阵,与弹性体的各向异性有关。ε为应变,满足下列公式:

式中:εij为应变张量分量;ui为i方向位移分量,m;uj为j方向位移分量,m;xi为i方向坐标;xj为j方向坐标。
对于平面问题,式(2)可简化为下式,具体参见文献[14]:
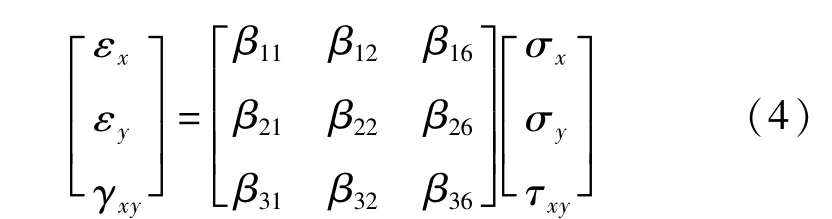
式中:εx为x方向的应变,无量纲;εj为方向的应变,无量纲;γxy为应变张量分量,等同于εij,无量纲;τxy为二阶应力张量分量,等同于为σij,Pa;σx为x方向的应力,Pa;σy为方向的应力,Pa;β11、β12、β16、……β36均为在x-y坐标系中计算的柔度分量。
在井壁及裂缝面上,其应力及面力应满足静力边界条件:

式中:pi为i方向面力分量,Pa;σij为二阶的应力张量分量,Pa;nj为静力边界外法线与j方向夹角的余弦;。
1.2 边界积分方程
弹性体边界上的边界积分方程[15]为:
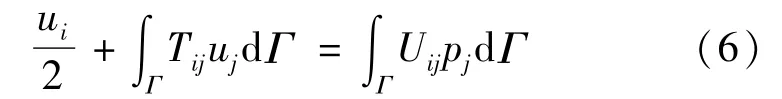
式中:Uij和Tij为当无限大平面弹性体内某一点(x0,y0)的j方向有单位集中力作用时,在任意一点(xk,yk)的i方向上的位移分量及应力分量;Γ为弹性体边界。
无限大地层中裂缝形态的计算需求解井壁(内部边界)及裂缝面的未知数。为方便计算,令Δuj=uj(C+)-uj(C-),则由式(6)可得井壁边界上的积分方程:
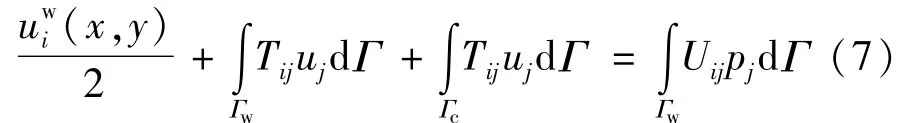
式中:uj表示j方向位移,m;Γw表示井壁边界;Tc表示裂缝面。
结合式(2)、(5),为提高计算精度,采用二次单元对边界进行离散化处理,由于水力压裂裂缝尖端具Δu~有的性质[11],因此,裂缝尖端单元可用二次插值函数表示为:

根据式(7)、(9),结合已知边界条件,可求得井壁及裂缝面处的位移及应力分布。
1.3 应力强度因子的计算方法
裂缝尖端相对位移Δu1、Δu2与应力强度因子KI、KII之间的关系为[17]:

式中:Δu1、Δu2为裂缝尖端相对位移,m;KI、KII为应力强度因子,Pa·;RΔu、H11、H12、H21、H22为中间计算单位变量。
水力压裂过程中裂缝以张拉形破坏为主,较少出现纯剪切破坏的情况,因此,为避免奇异性,J积分定义如下[18]:
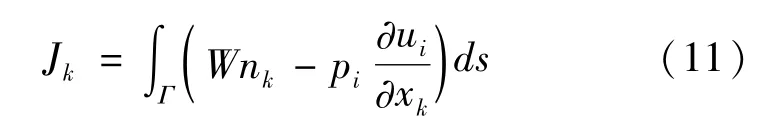
式中:W为应变能密度。
J积分与应力强度因子KI、KII关系为[19]:
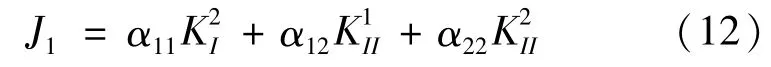
式中:α11、α12、α22均为在x-y坐标系中计算的柔度分量,这些分量与材料弹性参数有关。
将式(10)代入式(12)中,可求解应力强度因子KI、KII:
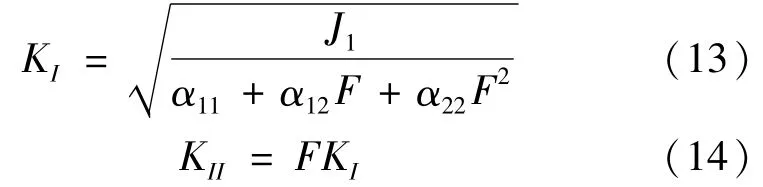
2 定向射孔压裂条件下裂缝扩展模型的建立及程序编制
2.1 物理模型的建立
在定向射孔的引导下,裂缝沿着射孔方向形成初始裂缝,并在井筒压力、远场地应力及缝内压力等因素的共同作用下延伸扩展,形成双翼弯曲缝。为研究裂缝形态,沿水平方向截取单位厚度的岩层为研究对象,建立定向射孔压裂条件下裂缝的扩展模型(图1)。射孔方向与最大主应力的夹角为θ,水平最大主应力为σH,水平最小主应力为σh。
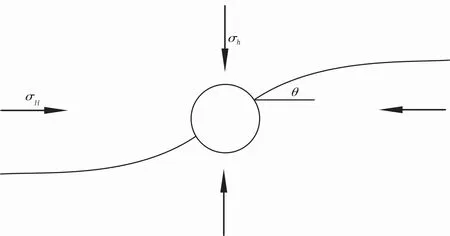
图1 模型示意图
2.2 各向异性地层中裂缝扩展准则
各向异性材料裂缝尖端应力场的计算公式与各向同性材料存在很大差别,基于各向同性力学所推导的裂缝扩展角计算公式并不适用于各向异性地层中裂缝扩展路径的计算。最大周向应力准则计算裂缝开裂角度简便,目前在工程上常被应用[20],故采用最大周向应力准则计算各向异性地层中裂缝的扩展路径。
裂缝尖端应力场可用应力强度因子KI、KII表示为:

式中:r为与裂缝尖端的距离,m;γ为与裂缝尖端的夹角,Re定义为复数的实部。
极坐标条件下裂缝尖端的周向应力可表示为:
σθ(γ)=σx1sin2(γ)-2τx1y1sin(γ)cos(γ)+

式中:σθ为周向应力,Pa。
根据最大周向应力理论,裂缝沿最大周向拉应力的方向起裂,因此,可将裂缝扩展的方位角的求解问题转换为带约束条件的非线性优化问题,即:

以上优化问题可通过单纯形法、大M法或对偶单纯形法等求解。
2.3 定向射孔压裂条件下裂缝发展形态的计算程序
基于二次单元的边界元计算方法可显著提高计算精度,但其高计算精度是以计算速度为代价的。以系数矩阵为例,与常单元的边界元计算方法相比,其系数矩阵的元素个数增大了9倍。由此可见,基于二次单元的边界元计算方法提高了计算的准确性,但是在计算时间上并没有什么优势。并行计算是提高计算机系统计算速度和处理能力的有效方法之一,其基本思想是将所求解问题分解成若干个子区域,各子区域均由一个独立的处理机处理,从而实现多计算资源的协同计算[21]。文中边界元计算时间最长的任务为系数矩阵的计算。由式(8)、式(9)可以看出,∫TijujdΓ、∫UijujdΓ、∫Tij,kujdΓ、∫Uij,kujdΓ的计算任务是相互独立的,并不需要通过数据传递以实现数值计算。因此,可采用并行运算方法将系数矩 阵 的 计 算 分 为∫TijujdΓ、∫UijujdΓ、∫Tij,kujdΓ、∫Uij,kujdΓ四个子区域进行,从而在保证精度的前提下提高计算速度。
按照以上理论及方法,编写了可模拟定向射孔压裂条件下裂缝发展形态的计算程序。模拟过程为计算裂缝的位移场及应力场分布,求出应力强度因子及裂缝扩展的方位角,并在裂缝尖端处延伸一小段二次单元,更新计算单元系数矩阵及单元编号,重复以上步骤,直到裂缝延伸至目标长度为止。
2.4 模型验证
A.Azhdari等推导了各向异性介质中远场应力作用下裂纹的应力强度因子解析式[22],M.Chertov求出了横向各向同性地层中缝内受均匀压力下裂纹的宽度分布解析式[23]。为验证所编制程序的正确性,将所计算的数值解与解析解结果相对比,计算参数为:弹性模量Ex=2.877 92 GPa,Ey=1.728 81 GPa,Ez=2.877 92 GPa,vxy=0.393 0,vyz=0.236 3,vzx=0.393 0,Gxy=1.100 0 GPa,Gyz=0.734 5 GPa,Gzx=0.734 5 GPa。计算结果见图2,从图2可以看出,本文所提的边界元计算结果与解析解结果吻合。
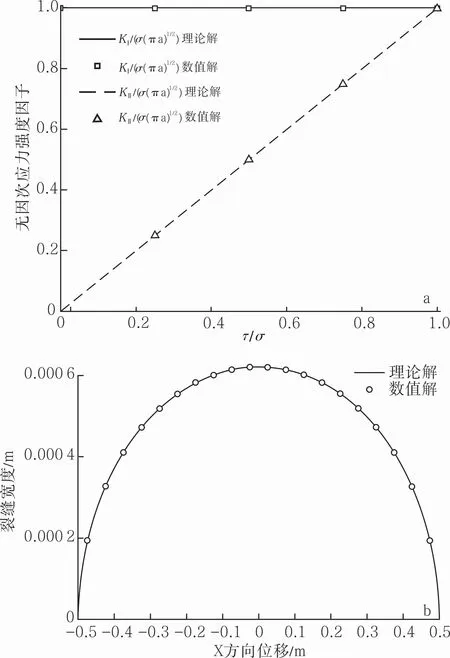
图2 计算结果对比
3 影响因素分析
为探讨各向异性地层中起裂压力的影响因素,取某煤层气储层[24]参数进行影响因素分析。其计算参数为:Ex=2.880 00 GPa,Ey=1.730 00 GPa,Ez=2.880 00GPa,vxy=0.393 0,vyz=0.236 0,vzx=0.393 0,Gxy=1.100 0 GPa,Gyz=0.730 0 GPa,Gzx=0.730 0 GPa,σH=19.28 MPa,σh=16.21 MPa。
3.1 弹性各向异性对裂缝形态的影响
不同弹性模量各向异性比值条件下的裂缝形态如图3所示。当定向射孔方向与水平最大主应力方向呈一定角度时,裂缝沿射孔方向起裂并延伸一段距离后,在远场地应力作用下逐渐转向水平最大主应力方向扩展,形成双翼弯曲缝[25]。根据最小能量原理,裂缝沿着阻力最小的方向扩展,当裂缝沿平行于水平最大主应力方向扩展时,由于所克服的应力为水平最小主应力,扩展阻力最小,因此裂缝的扩展方向均由射孔方向逐渐转向水平最大主应力方向。与理想的平直双翼裂缝相比,定向射孔压裂所形成的“S”形裂缝显著增加了裂缝与油藏的接触面积,提高了储层的动用程度,因此,定向射孔压裂技术有利于油藏的高产及稳产。

图3 K E(弹性模量各向异性比值)对裂缝形态的影响
定义弹性模量各向异性比值KE为Y方向上弹性模量Ey与X方向上弹性模量Ex的比值,显然比值越大,X方向上与Y方向上的弹性模量差别越大。从图3可以看出,裂缝Y方向上延伸距离随着比值的增加而缓慢增大,因此,随着弹性模量各向异性比值的增加,裂缝转向变缓,转向半径增大。但增长幅度较小。随着弹性模量比值的增大,由裂缝、井筒等所产生的诱导应力增加,会对井周原始地应力场产生了一定的影响,使得近井周区域水平应力差异性减小,裂缝更容易发生转向。
3.2 射孔角度对裂缝形态的影响
图4为不同射孔角度条件下的裂缝形态。由图可见,转向半径随着射孔角度的增加而增大。根据最小能量原理,裂缝延射孔方向起裂后均逐渐转向最大主应力方向扩展。当射孔方向与水平最大主应力方向夹角较小时(小于40°时),裂缝延伸较小距离后即可沿水平最大主应力方向扩展,因而转向半径较小。
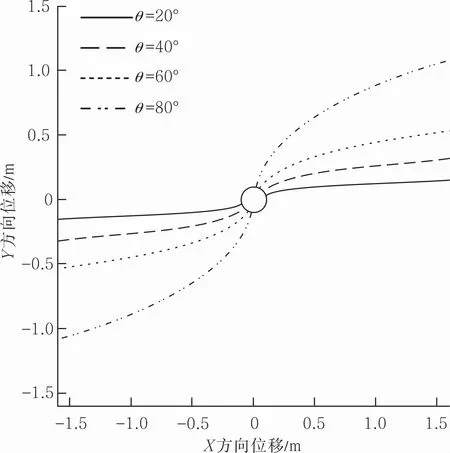
图4 射孔角度对裂缝形态的影响
不同射孔角度条件下的裂缝宽度见图5。由图可见,当射孔方向与水平最大主应力方向夹角过大时,裂缝宽度小。射孔方向与水平最大主应力夹角过大时(大于40°),裂缝扩展所克服的阻力为水平最大主应力和水平最小主应力的合力,夹角越大,水平最大主应力的分量越大,合力也就越大,因而裂缝宽度减小。在压裂作业过程中,由于裂缝的弯曲及宽度减小,沿程摩阻增大,会造成砂堵等复杂情况,不利于压裂增产作业。鉴于此,推荐射孔角度为0~40°。
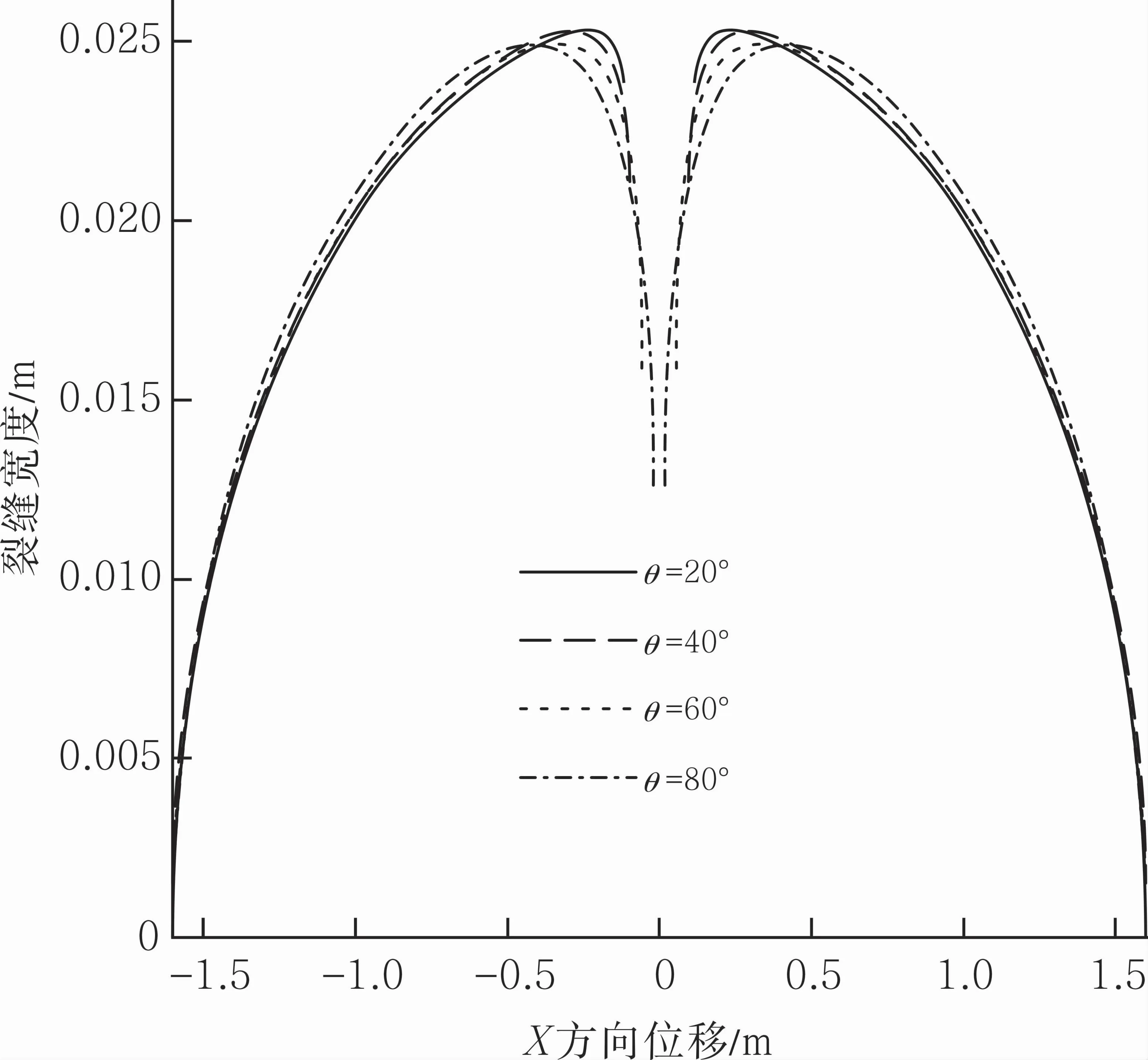
图5 射孔角度对裂缝宽度的影响
4 结论
(1)基于各向异性弹性力学和边界元方法,建立了各向异性地层中定向射孔压裂条件下裂缝的扩展模型,并通过最大周向应力准则提出了裂缝发展形态的计算方法。
(2)基于边界元法编写了定向射孔压裂条件下裂缝发展形态的计算程序,采用二次单元及裂缝尖端单元以提高计算精度,通过并行运算提高了系数矩阵的计算速度,从而在保证精度的前提下缩短了计算时间。
(3)当射孔角度与最大主应力方向呈一定角度时,裂缝为一条规则的“S”形裂缝。随着弹性模量各向异性比值的增加,裂缝转向半径略微增大,裂缝转向半径随着射孔角度的增大而增加。
