XRF结合化学计量学对牛皮纸物证的研究

孙家政，陆润洲，姜 红，满 吉

(1. 中国人民公安大学侦查学院，北京 100038; 2. 北京华仪宏盛技术有限公司，北京 100123)

0 引 言

犯罪现场的痕迹物证中，牛皮纸是一类经常出现的物证，它的存在形式包括信封、档案袋、手提袋、包装纸等等，但是现场提取到的牛皮纸往往只是碎片或者上面没有有用的文字信息，如果能够对牛皮纸实现分类鉴别，实现对于其种属类别的倾向性认定，可以给案件的侦破提供线索与突破口。例如在西安“2018·12·12”盗掘古墓葬案这起案件中[1]，如果能够对于举报的信封进行类别的倾向性鉴定，从而缩小其来源的范围，从而再结合掌握的信息和其他技术手段，进一步排查出潜在的举报人，可以给本案的前期侦查工作节省资源，提供线索与思路。

法庭科学中，对于纸类物品分类检验常有X射线荧光光谱法[2-4]、拉曼光谱法[5-6]、傅里叶红外光谱法[7]、扫描电镜法[8]等。X射线荧光光谱可以直接显现被检测物体光谱特征，而且也能准确测得元素的种类和含量，对于纸类的研究非常有用[9]。陈壮等研究不同品牌和批次的一次性纸杯，使用 X 射线荧光光谱仪测定其元素组成，结合定性和半定量分析法将31个品牌一次性纸杯分类[3]。郭鹏等应用波长色散型X射线荧光光谱仪对不同品牌不同系列的烟用内衬纸样品中的常量和微量元素进行定性和半定量分析，利用聚类分析法对这些烟用内衬纸样品进行分类[4]。此类研究中，都只是实现了对于研究对象的分类，但是对于在实际办案过程中遇到的某一新的具体的物证，仍然存在不能对其种属类别快速作出倾向性认定的局限。Fisher判别分析法在原有的数据进行分类的基础上，建立判别函数，实现对于新数据类别变量取值的预测。朱晓晗等研究不同品牌的一次性塑料手套，处理数据中使用了Fisher判别分析法，建立的第一和第二判别函数的特征值为97.313和10.682，累计百分比为 99.9%，取得了令人满意的实验结果[10]。

本文采集了50种不同种类和厂商的牛皮纸样本，用X射线荧光光谱仪测出元素含量。通过系统聚类和K-Means聚类，对测定结果进行分类和检验。在数据分类的基础上，使用Fisher判别分析法，建立判别函数，实现对新数据类别变量取值的预测。

1 实 验

1.1 实验仪器

实验仪器：X射线荧光光谱仪(X-MET8000 Expert型，英国牛津公司)，检测元素范围：12Mg～92U，元素检出限如图1所示。

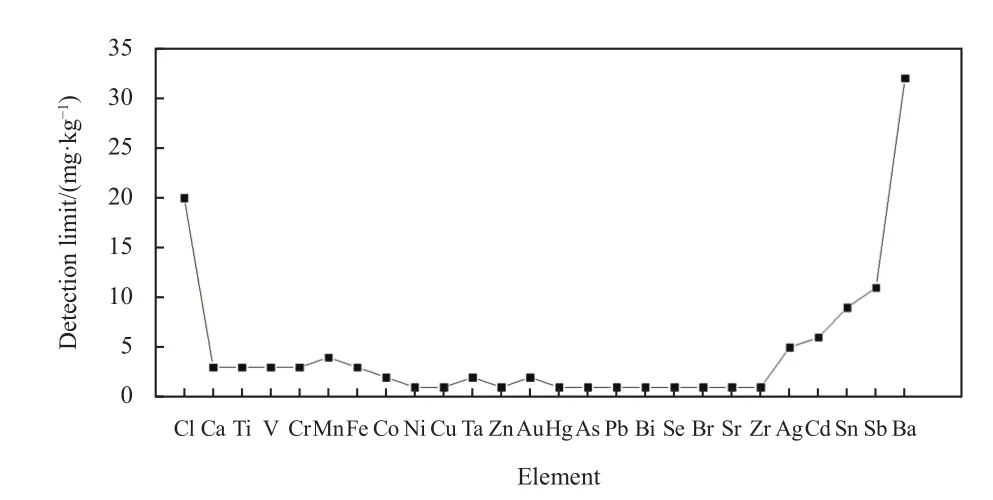
图1 X-MET8000 Expert的元素检出限

检测条件：Rh阳极靶，电压50 kV，电流200 μA，工作温度25 ℃，工作模式plastic。

1.2 实验样本

不同种类、不同厂家、不同用途的牛皮纸样本50个（见表1）。

表1 牛皮纸样本表

1.3 测试时间的选取

随机选取43样本“北京市教育委员会信封（北京天工印刷有限公司）”，在相同的条件下，分别用X射线荧光光谱仪测试 30，40，50，60，70 s，每个时间平行测定3次，取平均值进行分析，通过分析测试数值中主要元素的含量大小的变化，选出最佳测试时间。

通过对43样本不同测试时间分析（见表2），可以发现，当测试时间较短时，测试结果的数值随时间变化较大，不同的测试时间会对测得的元素含量的精度产生影响，这可能是由于在较短的测试时间内，取样点不够多，实验中峰值的出现是许多测试数据累加的结果，如果取样点较少，则会造成峰值参数不够准确[11]。当测试时间达到60 s以上时，测试结果的数值趋于稳定。综合测试结果的准确度和实验效率等方面因素的考量，选取60 s作为实验中的测试时间。

表2 43#样本的分析结果

1.4 重现性实验

随机选取5样本“中国人民公安大学信封（中）（廊坊市安次区码头庆富印刷厂）”，用X射线荧光光谱仪进行10次重复性实验，每次测定时间为60 s。

通过对于5样本的10次测试结果（见表3）进行计算分析可以发现，对不同元素检验结果的相对标准偏差均小于5%[12]，具有较好的重现性，因此可以得出结论，利用X射线荧光光谱法检验牛皮纸的实验结果是准确可靠的，可以利用该方法对牛皮纸样品进行分析检验。

表3 5#样本的分析结果

1.5 对牛皮纸样本的XRF测试

分别从50个样品上剪取面积约为10 mm×10 mm的样本，放置于仪器背景板上，用X射线荧光光谱仪进行测定，每个样本平行测定3次，取其平均值。

XRF测试结果显示，牛皮纸中含有的主要元素有 Cl、Ca、Ti、Mn、Fe、Cu、Zn、Sn、Ba等。Ca元素的主要来源是碳酸钙，它是纸张的常用填料[13]；Cl元素的主要来源是次氯酸钙和二氧化氯，它是牛皮纸在生产过程中用到的漂白剂；为增强纸张机械强度，造纸过程中常使用的复盐会引入Fe、Ti元素[14-15]；Cu元素的主要来源是硫酸铜，它在造纸过程中起絮凝除杂的作用；Zn元素的主要来源是硫酸锌，它是造纸过程中用到的增白剂；Sn元素的主要来源是亚锡酸钠，它是造纸过程中用到的防腐剂[2]；Ba元素的主要来源是硫酸钡，用于造纸填料，起增加纸张白度、平滑度等作用[16]。不同品牌、不同厂商、不同用途的牛皮纸样品由于原料和加工工艺不同，所含元素种类和含量也会有所区别。因此，经过初步的分析可以得出，样本中所含元素种类和含量可以作为样品区分的依据[17]。

2 分析与讨论

2.1 系统聚类法

为了实现对样本更准确的区分，在IBM SPSS Statistics 26.0软件中选用质心法对测试结果进行系统聚类（见图2），当并类距离为1时，样本可分为8类；当并类距离为2时，样品可分为6类；当并类距离为3时，样品可分为5类；当并类距离为5时，样品可分为4类；当并类距离为7时，样品可分为3类；当并类距离为14时，样品可分为2类[18]。

图2 50种牛皮纸样本聚类分析结果

2.2 K-Means聚类

为了验证系统聚类结果的准确性，以8为聚类数对测试结果进行K-Means聚类分析，分类结果（见表4）证实了通过系统聚类将50个样本分为 8类是较为准确的[19-20]。

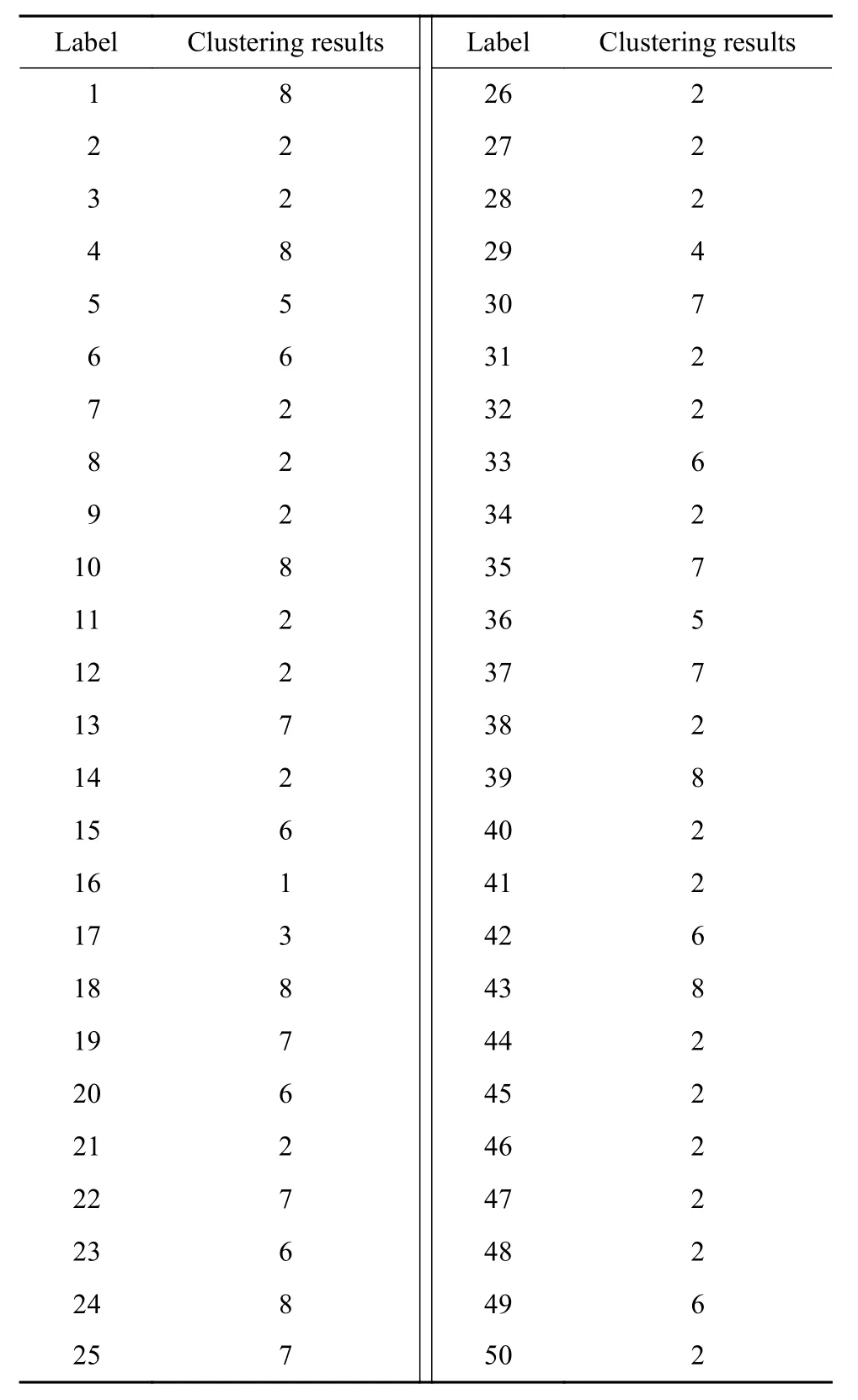
表4 样品 K-Means 聚类结果

2.3 Fisher判别分析法

以聚类结果为基础，在对样本区分的基础上，运用Fisher判别分析法，以达到对新数据类别变量取值进行预测的目的。

表5是 Fisher 判别函数的非标准化的系数矩阵，七个判别函数如下：

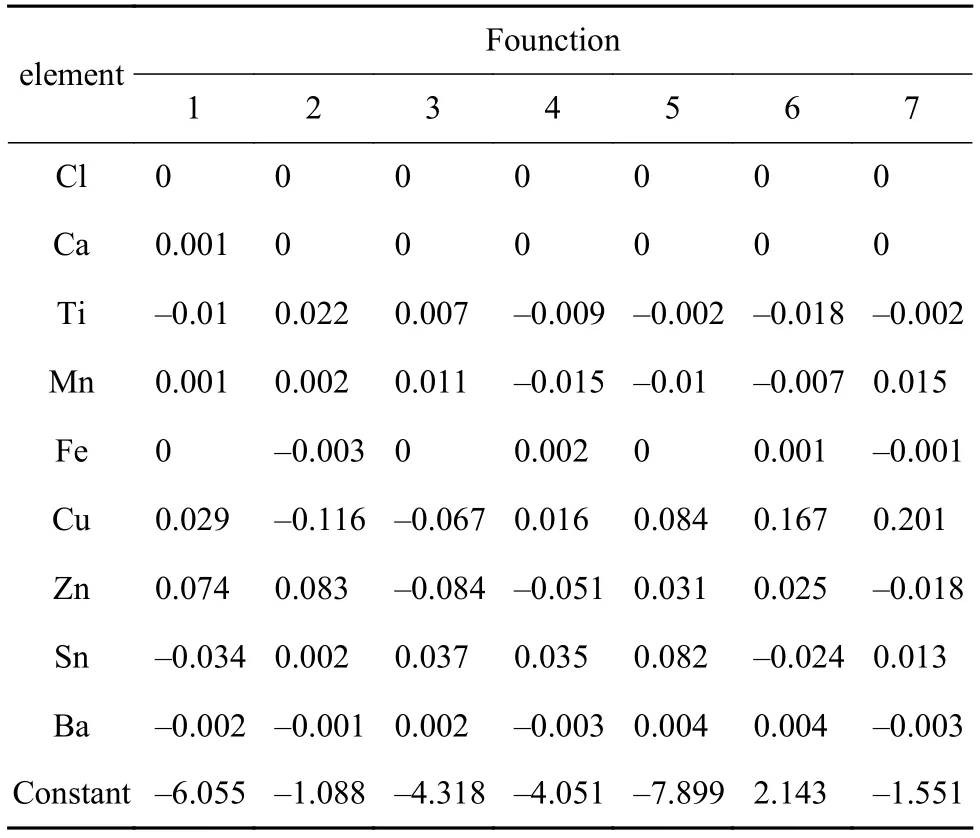
表5 典则判别函数系数

其中，变量X1为Ca元素含量，X2为Ti元素含量，X3为Mn元素含量，X4为Fe元素含量，X5为Cu元素含量，X6为Zn元素含量，X7为Sn元素含量，X8为Ba元素含量。

但是，这七种判别函数并不是每一种都能很好地实现对类别变量取值的预测（见图3）。第一判别函数的特征值为138.218，累计百分比为92%，第二判别函数的特征值为11.218，累计百分比为99.4%。典则相关性系数越大，说明该函数轴上的类别差异越明显，第一个判别函数和第二个判别函数明显优于其他五个判别函数，其余五个判别函数解释方差能力较低，仅有0.3%至0之间，可以略去，即 Fisher判别空间为二维空间。

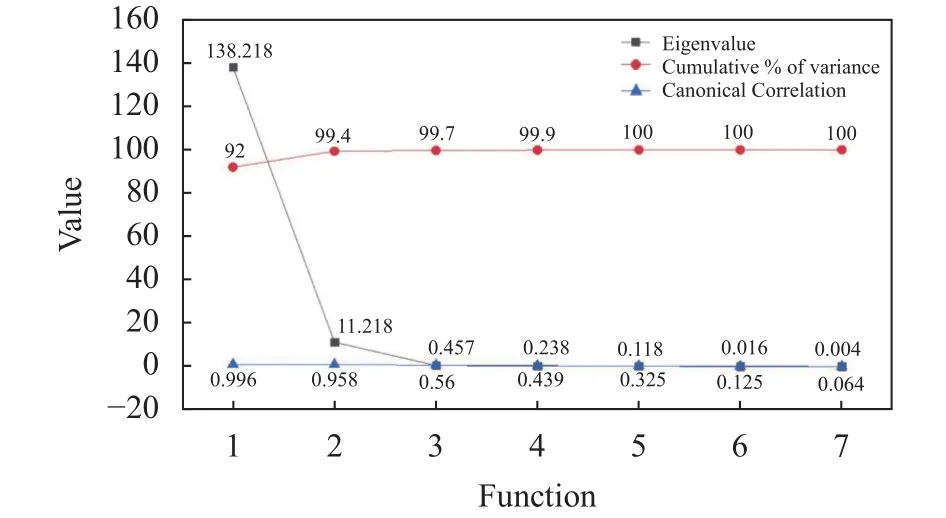
图3 判别函数特征值

为了验证上述判别函数一和判别函数二预测效果更好的结论，可以采用威尔克的λ ( Wilks’λi) 统计量反向测度。

式中：I——最后一个判别函数；

i——第i个判别函数；

Ejgenvalue——特征值。

可以得出，I值越小，整体判别能力越强。

检验统计量是在威尔克的λ基础上构建的，检验统计量关系为：

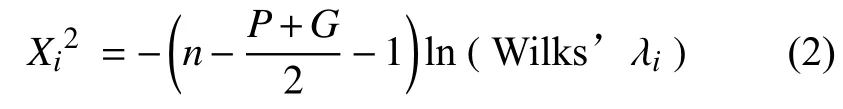
式中：Xi——检验统计量；

n——总的样本量；

P——判别变量个数；

G——类别数；

ln (Wilks’λi) ——小于 0。

在本实验中，n为50，P为8，G为8。该统计量近似服从卡方分布。当概率值小于显著性水平0.05时，认为当前判别函数整体的判别能力较强。图4中，函数检验1～7，检验统计量观测值为330.489，对应的概率值为0；函数检验2直至7，检验统计量观测值为130.58，对应的概率值为0.04。剩余的概率值都大于0.05，因此可以考虑舍弃第三至第七判别函数。

图4 威尔克 Lambda

所以，如图5，选择函数一和函数二作为判别轴建立的联合分布图。由联合分布图中可以看出，每个点的横坐标区分更加明显，纵坐标的区分效果较差，即判别函数一对于类别变量的预测结果要优于判别函数二。因此，在本实验中，判别函数一是对牛皮纸样本进行判别分类的最佳函数[21-22]。

图5 Fisher判别函数分布图

3 结束语

通过X射线荧光光谱法，对不同的牛皮纸样本进行检测，此方法简便快速、无需对样本进行特殊的前处理，且结果准确可靠。对测试结果进行系统聚类，可以将50种样本分为8类；然后使用KMeans聚类，对分类的结果进行检验，证明样本分为8类是合理的。依据聚类结果，使用Fisher判别分析法，建立7种判别函数，经分析验证，第一和第二判别函数判别能力较强，第三至第七判别函数判别能力较弱，以第一和第二判别函数建立Fisher判别函数分布图，分布图可以直观地反映出判别函数一的预测结果要优于判别函数二。

对于以后犯罪现场牛皮纸物证的检验中，可以直接运用判别函数一，对于提取到的牛皮纸物证可以进行快速的分类辨别，实现对于其类别的倾向性认定。也可以按照本文思路，选取数量更大、种类更为详细的牛皮纸样本，经过分析得出预测效果更佳的判别函数，对于犯罪现场提取到的牛皮纸物证，将其测试数据带入判别函数中，可以迅速地确定其种类和来源，为犯罪现场的牛皮纸物证的检验提供帮助。