均值漂移模型实现GPS/BDS导航完好性监测

虢 盛，徐进立，张绍成，苟鸿飞

（中国地质大学（武汉） 地理与信息工程学院，武汉 430078）

0 引言

全球定位系统（global positioning system, GPS）及北斗卫星导航系统（BeiDou navigation satellite system，BDS）进行组合导航定位时，不仅能通过增加卫星数量来提高导航定位精度，还能通过不同系统观测数据相互校验来保证用户导航定位的可靠性。

20世纪60年代，荷兰巴尔达（Baarda）教授提出了可靠性研究的基础理论，并在假设单一粗差和验前单位权中误差已知的情况下，推导得出了著名的“数据探测法”[1]，文献[2]将 Baarda 的数据探测理论应用于GPS基线解算中，提出了基于三种 GPS基线解算模型下的内部可靠性检验方法。文献[3]提出将粗差视为函数模型一部分的重要思想，进一步完善了可靠性研究理论。文献[4]探究了观测值相关条件下的内部可靠性原理，提出一种新的可靠性指标，解决了观测多余度值域超过[0,1]区间后的可靠性度量问题。

在GNSS接收机自主完好性评估方面，文献[5]研究了 GPS单系统及多系统组合增强型接接收机自主完好性监测（advanced receiver autonomous integrity monitoring, ARAIM）可用性性能。文献[6]则利用GPS/BDS兼容接收机双频实测数据及BDS布满星座假设下的仿真数据，通过改进不同卫星频点特征向量选择方法，提高了基于奇偶矢量法的接收机自主完好性性能，文献[7]将GPS/BDS卫星按星座分为两组，验证了最优加权平均解（optimal weighted average solution，OWAS）算法对30 m以上误差的双星多故障检测的可行性。

本文基于GNSS接收机中GPS和BDS观测数据的相互校验原理，来实现单一粗差探测。首先研究基于伪距残差的内部可靠性模型及经典接收机自主完好性监测（receiver autonomous integrity monitoring, RAIM）在 GPS/BDS双模导航定位中的基本理论；然后根据GPS/BDS伪距观测残差方差特性，基于均值漂移模型提出一种系统间均值校验的接收机自主完好性粗差探测方法；最后通过实测数据的异常模拟，与经典 RAIM 法进行对比，来验证了本文算法的可行性和优越性。

1 内部可靠性数学模型

1.1 内部可靠性模型

可靠性检验理论作为用户导航定位完好性监测的重要研究内容，主要分为外部可靠性和内部可靠性两方面。外部可靠性主要研究未剔除粗差对结果影响的大小，即抵抗粗差的能力[8]。内部可靠性是指在平差过程中发现并剔除粗差的能力[9]。

本文重点讨论单一粗差假设下的GPS/BDS伪距残差内部可靠性检验方法。当伪距观测值中不存在粗差时，H0假设为

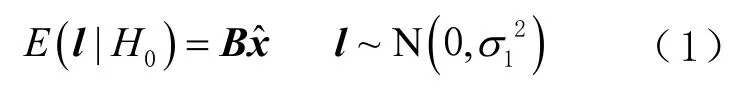
当伪距观测值中存在粗差时，H1假设为

基于上述假设，构建内部可靠性检验模型寻找可能出现的卫星导航定位服务异常事件。

当服从H0假设时，线性化误差模型为

式中：l为n ×1维观测值向量；v为n×1维改正数向量；B为n×m维观测值矩阵；x︿为m×1维待估向量。观测值权阵P为n×n阶矩阵。

根据最小二乘准则vTPv=min可知

参数估值为

对应改正数为

改正数的协因数阵为

根据可靠性理论可得

通常将矩阵R对角线上的值作为可靠性量度（ri=Rii），其数值越小，表明对应的观测值可靠性越差；反之可靠性越好。当观测值之间相互独立时，可靠性量度ri∊[0,1]；而当观测值相关时，可靠性量度ri取值可能大于1。在观测值相互独立时，ri=1表明对应观测值为必要观测；ri=0则表明对应观测为多余观测[10]。

若观测值向量无粗差，则ˆx的估计值是无偏的，用间接平差求解即可；若观测值向量中包含粗差，那么上述的估计值是有偏的，即拒绝H0假设，接受H1假设，线性化误差模型为

式中：H为n ×k维粗差向量；s︿为k×1维未知粗差[11]。

根据均值漂移函数模型，可得对应法方程为

因此可知未知粗差的估值为

1.2 经典粗差探测法

经典 RAIM 算法主要有快照式算法、伪距残差比较法和奇偶矢量法，且已有学者证明了三者的等价性[12]。这里介绍的经典粗差探测法是在伪距残差比较法基础上，将 GPS/BDS观测值按 2.1节总结的基于最小二乘的间接平差法处理，从而构建卡方分布检验统计量探测完成粗差探测的过程。统计量F定义

式中：n为GPS和BDS卫星数之和；v为卫星观测值残差；P为相应的权阵。

观测方程含测站三维坐标及对应GPS/BDS不同系统接收机钟差 5个待估参数。若伪距观测值无粗差，则理论上残差向量满足零均值的正态分布，进而F满足自由度为n-5的卡方分布。

根据用户需求定义完好性误警概率PFA即可确定对应的检验限值F，具体公式[13]为

式中：fχ(n−5)(x)为卡方分布的概率密度函数；为GPS与BDS伪距观测方差。

1.3 基于均值漂移的粗差探测法

经典粗差探测法是将粗差视为随机模型一部分，有粗差的观测值相比其他观测值具有相同的期望、较大的方差，因而通常称为“方差扩大模型”[14]；此外，还可将粗差视为函数模型的一部分，含粗差的观测值相比其他观测值具有不同的期望，在方差相同、期望的不同条件下，观测量会呈现非中心化分布，因此也称为“均值漂移模型”[15]。

无粗差时，GPS/BDS伪距改正数vFull满足零均值的正态分布，即

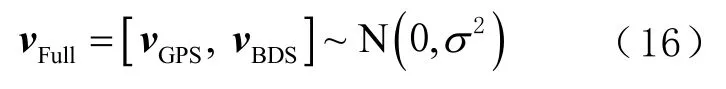
但在单个历元有限可视卫星条件下，伪距残差均值μ通常不绝对等于零，其统计结果可表达为

式中：μ1、μ2分别为 GPS和 BDS伪距残差期望，对应残差方差分别为和。

以武汉地区的国际 GNSS服务（International GNSS Service, IGS）九峰站（JFNG）2020年12月1日24小时GPS/BDS观测数据为例，GPS和BDS L1和B2频点残差序列统计值如图1所示。

图1 JFNG 2020年11月30日GPS/BDS的残差分布

由图1可见，无粗差条件下GPS/BDS伪距残差趋近于零均值；但GPS残差方差σ12=2.41 m2而BDS方差σ22=4.44 m2，存在一定差异。

按均值漂移模型对GPS/BDS伪距观测值分别平差，并构建一个新的内部可靠性检验统计量，即偏离量K。K定义为BDS和GPS独立伪距残差分布期望值之差，计算方法为

进一步构建T统计量，检验偏移量K值差异，并按式（15）计算对应检验门限值。通过比较检验统计量T与检验门限值大小即可完成故障检测。

假定两独立样本方差未知且不等情况下，采用萨特思韦特（Satterthwaite）近似法构造T统计量[16]为

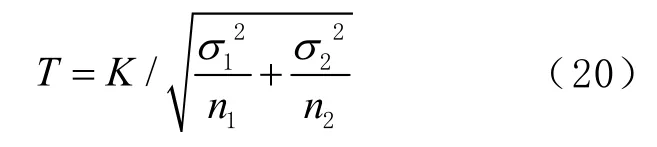
对应自由度N表达为

式中，ni（i=1,2）为GPS/BDS卫星数量。

采用均值漂移定律解算含粗差伪距值，虽然能大幅度减弱残差样本方差的放大，但在 GPS/BDS可视卫星20余颗的条件下，残余方差失真效应不可忽略。本文基于GPS/BDS伪距残差先验信息取代 GPS/BDS伪距残差方差，根据图1统计结果，设定GPS和BDS先验方差分别为2.5 m和4.5 m。

本文改进内部可靠性检验方法概括如下：

1）建立假设检验：H0认为该历元存在粗差；H1认为该历元不存在粗差。并假设第i颗卫星存在粗差，此时式(9)中粗差向量H(i)=1,其余元素均为0。

2）根据式（9）至式（13）计算对应的粗差估值s︿、伪距残差v，并按 GPS/BDS方差先验信息，重构GPS/BDS观测值方差。最后根据式（21）至（22）式计算检验统计量T。

3）循环n次（n表示 GPS/BDS卫星数量之和），并选择最大值Tmax与按式(15)计算的检验门限值比较，Tmax较大则认为该历元存在粗差，并求得对应的伪距残差v 和粗差估值s︿ 。本文式(15)中误警概率PFA≤0.01。

1.4 最不可探测卫星

在内部可靠性检验中，最小可探测误差（minimal detectable bias ,MDB）是一个很重要的指标，其表示在一定的检验功效以及一定的显著水平下，可发现粗差的下界。

若只有一个粗差的单个备选假设下，其最小可探测误差为

式中：Mi为第i颗卫星对应的MDB值；λ0为非中心化参数；σ0为验前单位权中误差；P为权；Qvv为改正数的协因数阵。根据式（8）可靠性矩阵R，可将式（22）改写为

从式（23）中可以看出，当非中心化参数、验前单位权中误差以及对应观测值的权一定时，M和可靠性量度值成反比。当可靠性度量参数ir越大时，观测值可靠性越高，所对应的M值越小，进而认为MDB值最大的卫星为最不可探测卫星。

2 算例分析

选取2020年12月1日JFNG站的GPS和BDS双模观测数据，设定卫星截止高度角 10°，L1/C2信噪比大于30 dB，并摒弃轨道误差较大的BDS 地球静止轨道（geostationary Earth orbit,GEO）卫星后，画出当天可见卫星数和位置精度衰减因子（position dilution of precision, PDOP）值如图2所示，该观测时段内可见GPS/BDS卫星数分别在 6~13颗和 12~19颗之间，对应 PDOP值在 1~2之间， GPS/BDS可视卫星具有较好的空间几何分布。

图2 JFNG站点可见卫星数/PDOP值

基于改进粗差探测方法计算无粗差情况下检验效果如图3所示，当GPS/BDS伪距观测值中未包含粗差时，T统计量整体小于检验门限。表明当观测值中无粗差时，BDS和GPS系统残差期望无明显差异。

图3 无粗差下T统计量

当对 BDS最不可探测卫星 C2频点上分别添加10、20、30 m粗差后，其检验效果如图4所示。

图4 本文RAIM法添加10，20和30 m粗差后T统计量示意图

统计分析结果表明，当人为在最不可探测卫星上添加大小为10 m的粗差后，共有1 381个历元的检验量T大于其对应历元下门限值；添加粗差量增至20 m后，观测时间段内有2 794个历元的T值大于门限值，表明有95.5%的概率可以探测并剔除大小为20 m的粗差；添加粗差量再次增加至30 m，共有2 863个历元无法通过检验，对应粗差探测成功百分比为99.4%。

如图5所示，对比经典 RAIM探测效率图并将改进方法与经典 RAIM 方法探测成功百分比差异统计如表1。经典探测法对20 m以下的微小粗差较不敏感，人为添加10、20 m粗差的探测成功百分比仅为 0和 3.2%。而本文的改进方法对 10、20 m粗差探测成功率分别提高了 15.5%、36.7%，表明该方法较经典 RAIM 法而言，能够有效剔除量级为20 m的粗差。

图5 经典RAIM法添加10，20和30 m粗差后F统计量示意图

表1 经典RAIM算法不同粗差探测率统计表

3 结束语

本文通过分析 GPS/BDS伪距残差期望和方差特性，提出了一种基于GPS/BDS伪距残差均值差异的内部可靠性检验方法。利用伪距观测值中存在粗差时，GPS/BDS独立伪距残差分布之间存在非中心化这一特点，构造统计量T，在漏检率PFA＜1%条件下确定对应检验门限值，判断系统是否存在硬件级粗差。模拟粗差探测实验是在GPS/BDS实测数据上人为添加粗差，验证了本文所提出的可靠性检验方法能够准确、高效地实现粗差探测。GPS/BDS双系统不仅能够提高定位精度，而且还可以进一步保障导航数据的完好性。