基于自适应通信拓扑的无人机集群弱路径约束下的分布式控制器设计

刘金龙，张泽旭，徐田来，邓涵之

(1. 哈尔滨工业大学飞行器动力学与控制研究所，哈尔滨 150080；2. 济南大学自动化与电气工程学院，济南 250022)

0 引 言

随着无人机集群相关技术的不断研究，人们将其应用到更加复杂的环境中。美国国防预先研究计划局(DARPA)开展了多项针对无人机集群的项目研究，包括Perdix、CODE、LOCUST、Gremlins、OFFSET等，这些项目的研究将为美军作战带来巨大优势，甚至可以重新定义战争形式。

无人机集群协同控制是无人机集群飞行的重要一环，目前发展的协同控制方法主要是采用主从式方法、虚拟结构法、基于行为法和一致性方法的变体或几种方法组合的控制架构，且在满足一定行为的基础上，最终目标均是达到集群目标状态的一致性。国内外学者已经开展了大量而深入的研究，这些工作基本沿着协同控制器设计和集群仿生学建模两类研究方向展开。

从协同控制器设计的方向来看，Desai等提出一种主从式方法，通过反馈线性化令跟随者的相对位置达到指数稳定。Lewis等提出虚拟结构法，将编队看作一个虚拟的刚性结构，机器人作为其中的刚性粒子，通过3台机器人实物实验验证了算法的有效性。毕鹏等设计了基于一致性理论的非线性控制器，并通过变通信拓扑下航天器编队仿真校验验证了控制器的有效性。张世杰等设计了一种满足状态约束和控制输入约束的分布式协同控制器，并通过仿真校验验证了控制器的有效性。周健等考虑无角速度测量外部扰动和系统参数不确定条件，设计一种有限时间滑模协同控制器，仿真校验验证了控制器的有效性。马鸣宇等针对多航天器姿态协同问题设计了一种基于SO(3)的滑模协同控制器，解决了姿态奇异问题，并通过仿真验证了控制器的有效性。Yu等针对无人机，利用模糊神经网络估计传感器故障和模型不确定性，设计了一种分数阶容错协同控制器。薛向宏等考虑主从式航天器编队中存在的通信、碰撞等约束，设计了一种非线性干扰观测器和人工势函数的分布式协同控制器，可以在初始通信拓扑连通的情况下保持拓扑连通，最后通过仿真验证了算法的有效性。

从集群仿生学建模方向来看，这方面的研究工作探索基于自然界的集群运动进行建模，由智能体间相互作用聚集形成集群运动。Reynolds仿照自然界集群运动形式，提出了著名的Boid模型，通过鸟群的仿真最终达到了集群速度的一致性。Vicsek等在Boid模型基础上进行了模型改进并使集群出现了新的运动形式。Gabor等在Boid模型的基础上，考虑惯性、噪声、通信约束、时间延迟等因素，进行了二维环境下不同集群规模、不同速度、不同场景的集群仿真实验，并进行了30架的无人机室外飞行试验，验证了算法的有效性和稳定性。Li等在Boid模型的基础上，考虑到通信距离限制，设计了一种分布式协同控制器，并通过多固定翼无人机的仿真验证了控制器的有效性。Liang等以欠驱动无人车为对象，设计了基于集群中心位置的制导律，并融合人工势场以完成避障动作，实现了多无人车跟随路径的自主避障运行。

以上这些传统控制方法由于飞行构型固定且需要为每个智能体规划路径，给实时计算应用带来负担，并且其通信拓扑不具有良好的可扩展性。在无人机集群的某些任务中，如长途奔袭只需要集群从起点沿规划路径到达终点，对集群相对构型和单机路径的规划没有严格要求，这类任务可以从三个方面进行约束：

(1)弱路径约束，无人机集群仅仅规划一条路径，集群沿路径飞行，这就要求无人机间具备良好的防撞措施；

(2)无严格构型约束，无人机集群沿规划的弱路径飞行中不要求严格的集群构型；

(3)自适应通信拓扑，不要需要集群全通信拓扑，根据最近邻无人机原则构建局域通信拓扑。

目前国内外面向该约束的协同控制方法研究较少，本文针对该问题进行了系统研究，针对约束(1)设计基于LQR的控制器，以完成无人机集群沿一条规划的路径飞行；针对约束(2)设计了一种机间势能函数来模拟机间作用力，保持机间距离，无人机自主形成稳定的集群构型；针对约束(3)参考自然界鸽群、椋鸟群的通信拓扑形式，设计基于仿生的自适应通信拓扑以消除机间防撞带来的抖振，提高集群飞行稳定性。

本文第一节进行固定翼无人机运动学建模；第二节阐述自适应通信拓扑的主要流程，以解决约束(3)；第三节设计分布式协同控制器，包括一致性部分和机间防撞两个部分，分别解决约束(1)和(2)；第四节进行仿真校验与结果分析；第五节阐述结论。

1 固定翼无人机运动学建模

本文突出针对固定翼无人机集群的集群控制器设计，简化单无人机动力学模型。对于第个无人机，其运动学模型描述为

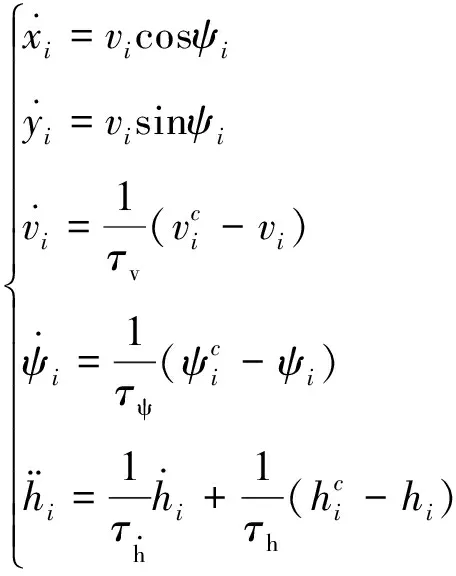
(1)

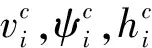
此外，无人机应满足固定翼无人机在水平速度、角速度和竖直速度的约束:

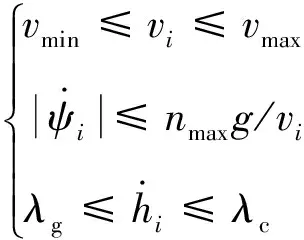
(2)

式中：,为速度上下限；为水平最大过载；为重力加速度；,为爬升、下降速度上限。

在集群的角度，是将单机看作一个质点，无人机的模型可以看作

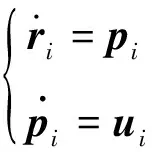
(3)

式中：,为无人机的位置矢量和速度矢量；表示相应的控制输入。定义无人机的状态空间为

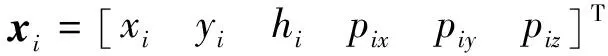
分别为无人机的位置矢量和速度矢量。则无人机的质点运动模型可以写为

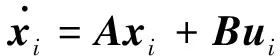
(4)

式中：

定义无人机与期望状态之间的状态误差为

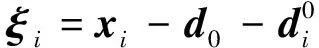
(5)

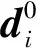
对误差变量求导可得

(6)

因此单机的质点运动模型可以表示为

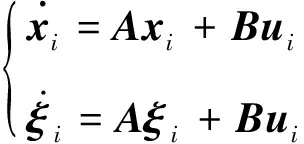
(7)

将其扩展到整个集群，则有

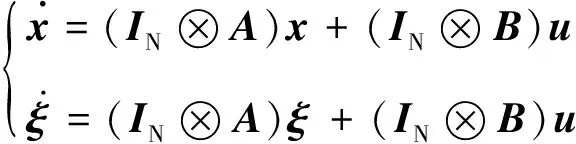
(8)

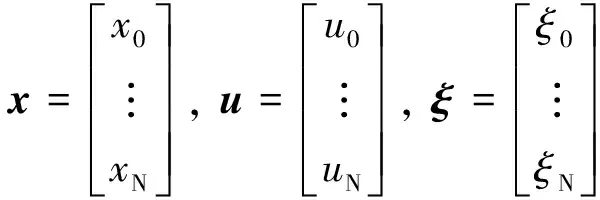
式中：⊗表示克罗内克积；,,分别为

2 自适应通信拓扑

本节仿照自然界中鸽群、椋鸟群等飞行时的通信机制应用到本文的协同控制中。自然界中的椋鸟、鸽子等鸟类在成群飞行时，其中的单体并不是与一定距离内的所有其他个体都通信，而是只与最近的几个邻居个体进行通信(小规模的鸽群为0～2只，大规模椋鸟群为6～7只)，而不考虑通信距离问题，因为只要目标个体在视线内就可以抵近并进行通信，采用这种通信方式的一大优点是通信负载不随集群密集程度变化而变化，即单个无人机不会因机间距离很大而失去通信，也不会因机间距离过小而导致通信负载过大，集群结构更稳定。但两者都会产生抖振现象，且基于距离的通信拓扑抖振现象更严重。

本文基于后者的通信形式设计通信拓扑。通过一系列仿真校验，若硬性规定通信的邻居数，假设为，则会产生第和第+1个无人机(或更多个无人机)的距离相差很小的现象，从而导致不同时刻考虑的无人机不同，而产生抖振现象。为解决此问题，本文不对通信邻居数进行硬性规定，而采用浮动的通信邻居个数，即由其自身所处的相对环境自主决定通信邻居个数：若根据第+1、第+2…个无人机所计算的距离差均小于一个设定阈值，则全部纳入通信邻居集合内，而若通信数量大于通信邻居数上限，则将所有+1及以外的无人机全部作不通信处理。本文称之为自适应通信拓扑。

该算法的核心是获得无人机的通信邻居集合与相应的状态和相对距离矢量信息。图1为某次迭代过程中获得无人机的邻居集合的流程图。

假设预定的通信邻居数为，通信邻居数上限为，则针对无人机，算法步骤如下：

(1)初始化通信邻居集合为空，根据距离由小到大，获取最近的=个无人机的信息，将其纳入通信邻居集合内；

(2)获取第+1个无人机的距离信息并与第个无人机的距离作差，若其差值小于某个设定阈值则将其纳入邻居集合内，继续向下一无人机扩展，重复步骤(2)；若其差值大于阈值则不纳入邻居集合内，并停止向下扩展，进入步骤(4)；

(3)若扩展到第+1个无人机，计算的距离差值仍小于设定阈值，则将第+1以后所有无人机信息全部舍弃，而只与前个邻居无人机构成的邻居集合通信；

(4)使用邻居集合内所有无人机的信息进行分布式协同控制的计算，并进入下一时刻，直到完成给定任务。

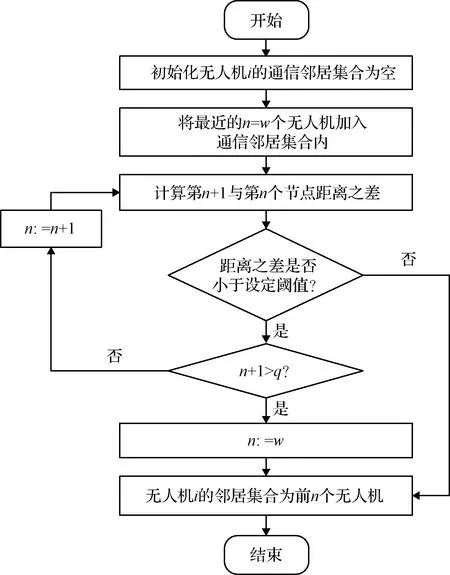
图1 某次迭代过程中获得无人机i的邻居集合过程图Fig.1 Gathering process of neighbors of UAV i during one iteration

该方法旨在以无人机为中心形成一个相对独立的、局部的“球”状集群，多个局部球重叠形成整个集群，同时为了提高集群稳定性，根据多次仿真的经验，单机最小通信邻居数需要比较小。

3 分布式协同控制器

本节基于前文建立的模型设计分布式协同控制器，控制器将基于自适应通信拓扑结构，并且分为一致性和机间防撞两个部分，对于无人机，其控制器表达式为

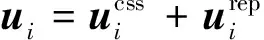
(9)

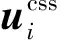
3.1 基于LQR的一致性控制器设计

本节根据前述质点运动模型设计状态反馈分布式控制器，并证明其稳定性。

对于系统(8)，给定正定矩阵∈、∈，选定系数满足

≥1((+()))

式中：是集群通信拓扑对应的拉普拉斯矩阵，表示集群内部的通信情况;是的最小特征值。若存在矩阵满足以下黎卡提方程：

++-=

(10)

则下述控制器可使系统保持稳定。

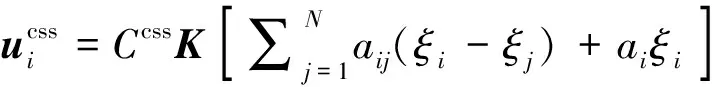
(11)

式中：=；代表无人机与之间存在信息交互，为无人机对通信(当值为0时表示不存在从到的信息流，值为1时表示存在从到的信息流)；代表无人机与期望状态之间的信息流，表示无人机是否接收到期望状态的输入(当值为0时表示无人机没有期望状态的输入，值为1时表示无人机有期望状态的输入)。

将式(11)扩展到整个集群可表示为

=(⊗)

(12)

将式(12)代入系统(8)的误差形式中可以得到

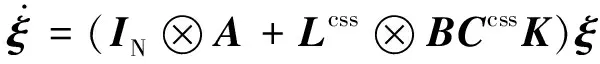
(13)

选择式(13)的一个李雅普诺夫函数候选为

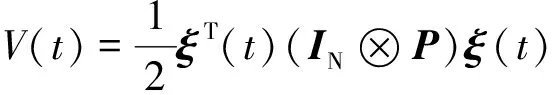
(14)

对其求导，并代入式(8)可以得到

())⊗]

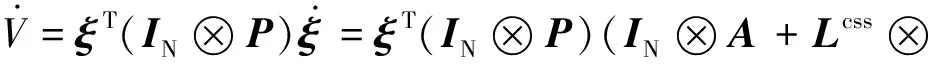
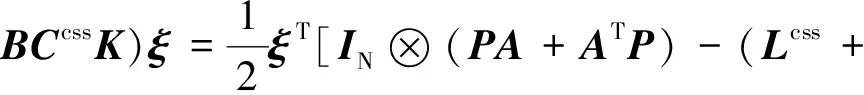
(15)

令

≥1((+()))

则可得

(+())≥

代入到式(15)中得到

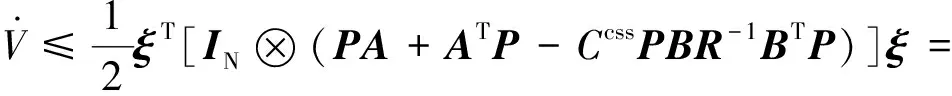
(16)

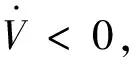
此外，根据LQR原理可知，该一致性控制器满足以下能量函数最优

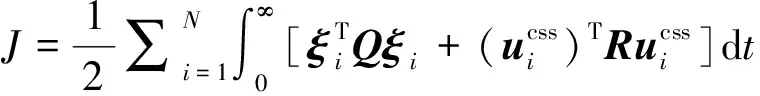
(17)

3.2 机间防撞设计

本文所涉及的集群控制概念，指的是可以把整个集群看作一个整体进而执行任务。若单纯根据前节控制器进行集群控制，可能出现两个无人机间距过小甚至发生碰撞。为防止碰撞的发生，集群内部需要具有机间防撞能力；同时若有无人机远离集群则需要控制其回归集群以避免丢失。本小节将建立集群内的机间势能模型，设计控制器的机间势能部分。

对于质点运动学模型，给出机间势能表达式为

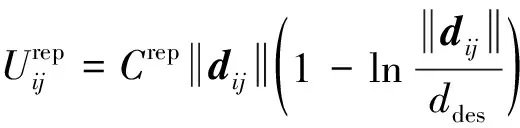
(18)

对应的机间作用力为

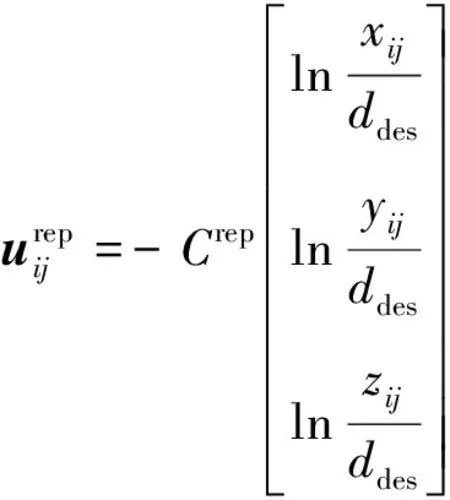
(19)

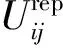
由表达式可得出作用力曲线在机间距离小于时为正，代表此时无人机与之间为“排斥”状态；机间距离等于时为0，此时无人机与之间没有相互作用力；机间距离大于时为负，代表此时无人机与之间为“吸引”状态。

在此基础上，加入建立的自适应通信拓扑，将无人机受到的所有作用力进行矢量加和得到

(20)

扩展到整个集群的控制器形式为

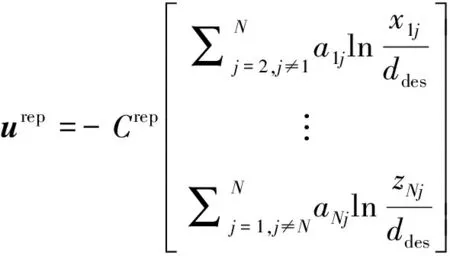
(21)

得到了一致性控制部分和机间势能控制部分后，就得到了本文的集群控制器，即为两个部分的加和

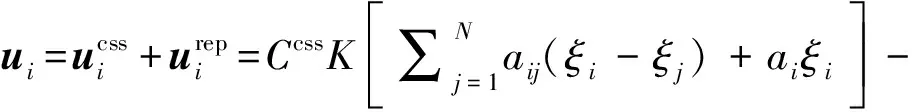
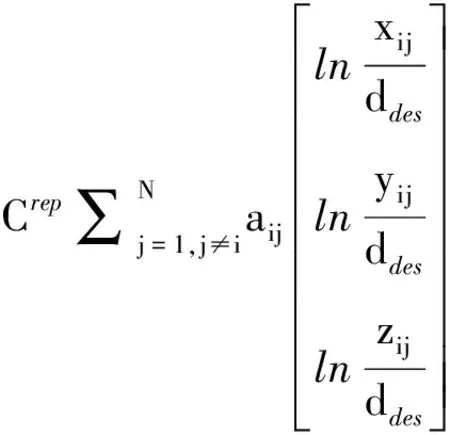
(22)

4 仿真校验

本节针对前述的集群协同控制器进行仿真校验，从两个部分验证控制器的有效性：弱路径规划部分用于验证本文控制器在减少输入方面的优越性；通信拓扑部分用于验证自适应通信拓扑对参数抖振的抑制效果。

主要仿真参数如表1所示。

仿真环境为：环境中存在障碍，障碍为以(314.20, -150.00) m为圆心、200 m为半径的圆形障碍，以及中心位于(1084.80, 200.00) m、长为284.80 m、宽为400 m的矩形障碍。无人机集群从初始位置(0, 0, 0)，到达目标点位置(1342.40, 100.00, 13.42) m。

表1 仿真主要参数Table 1 Main parameters in the simulation

首先为集群规划期望路径，假设设计输入的期望路径函数分为两段

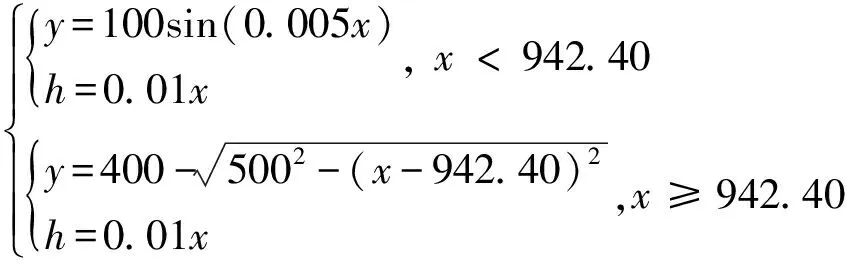
(23)

第一段路径水平投影为正弦曲线，第二段路径水平投影以=(,)=(942.40, 400.00) m为圆心、=500 m的圆弧的一部分。期望水平速度为=10 m/s，方向为沿路径水平投影的切线方向。

需要计算路径是否满足无人机运动学约束。第一段期望路径，根据计算得到水平速度,分别为

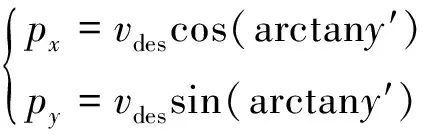
(24)

式中：′和为对的导数，有

′=05cos(0005)

进一步可以得到

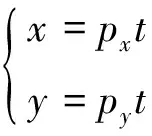
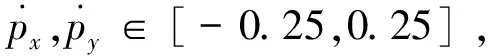
偏航角速度可以满足约束。

第二段期望路径对求导得到

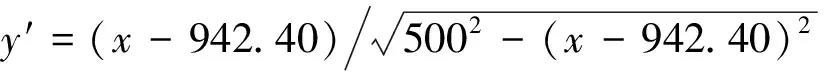
接下来验证第二段期望路径，根据计算得到水平速度,分别为

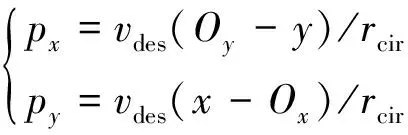
(25)

期望水平速度为10 m/s，可保证第二段期望路径满足无人机的速度约束；对于圆弧路径，其角速度为

==002

因此，对于偏航角速度有

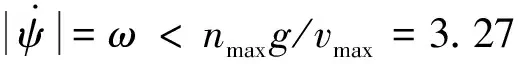
偏航角速度可以满足约束。

两段路径连接点为(942.40, -100.00, 9.42) m，两条期望路径函数在该点曲线连续，一阶导数也连续(水平方向均为0，竖直方向均为0.01)，水平速度恒为，竖直速度均为001，因此速度矢量也连续。

本文设计的期望路径目标状态(三轴位置和速度)全程满足连续约束，因此可以作为集群飞行的期望路径。

4.1 弱路径规划部分

为验证本文设计控制器在减少输入路径和避免设计集群构型上的优越性，仿真校验部分设置实验组和对照组1。实验组的控制器采用式(22)，对照组1采用式(11)作为协同控制器，即对于无人机，其协同控制器为：

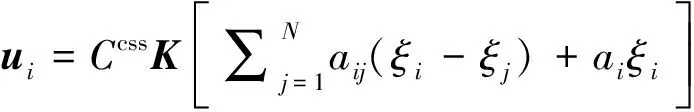
无人机初始位置为(0, 0, 0)～(50, 40, 0) m、间隔10 m的矩形分布，初始速度均为(7.07, 7.07, 0) (m/s)，目标点位置为(1342.40, 100.00, 13.42) m，仿真步长0.1 s。对照组1中期望集群构型为三路纵队的矩形阵，期望机间距离为10 m，2号无人机的期望路径函数为式(23)，其他无人机与2号无人机保持相对构型；实验组期望路径只有一条，为式(23)。

图2为对照组1和实验组在仿真过程中三个时刻飞行状况的俯视图，其中圆柱和长方形区域为障碍，小圆圈表示三个时刻无人机集群位置，实线表示无人机集群期望路径(对照组选取四个典型无人机的期望路径，实验组仅有一条期望路径)。三角形为起始点，坐标(0, 0, 0) m，五角星为目标点，坐标(1342.40, 100.00, 13.42) m。对照组1中每个无人机都有一条期望路径，实验组中所有无人机的期望路径只有一条，无需设计集群构型。

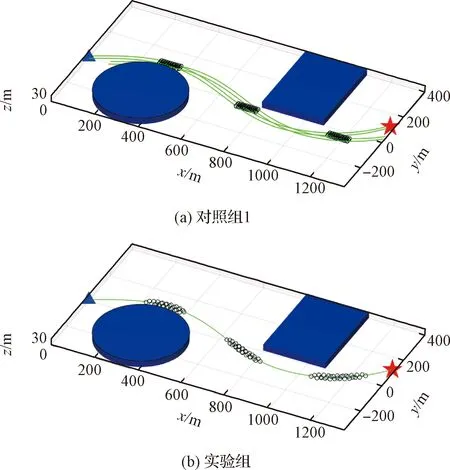
图2 三个时刻集群飞行状态图Fig.2 Swarm flight states at three different moments

从图2中可以看出两组集群的飞行轨迹最终都收敛于期望路径。但对照组1需要输入多条路径，输入路径数目等于集群中无人机数目，同时需要输入机间的相对构型，而实验组仅需要输入一条路径，无需设计相对构型，集群就可以沿规划路径稳定飞行。因此本文设计的协同控制器避免了复杂的输入。

4.2 通信拓扑部分

为验证本文设计的自适应通信拓扑在抑制抖振方面的优越性，仿真校验部分设置实验组和对照组2，两组的控制器均为式(22)，实验组集群的通信拓扑为本文设计的自适应通信拓扑，对照组2集群的通信拓扑同样为与最近的数个邻居通信，但邻居数量固定为6。

所有无人机均可获得期望路径，自适应通信拓扑用于机间防撞部分。期望路径函数均为式(23)。无人机初始位置均为(0, 0, 0)～(50, 40, 0) m、间隔10 m的矩形分布，初始速度均为(7.07, 7.07, 0) (m/s)，仿真步长0.1 s。两组集群仿真飞行状态与图2(b)一致。

图3～7为对照组2和实验组仿真结果图。图3为集群内最小距离随时间的变化曲线，其中实线和虚线分别表示实验组和对照组2集群最小距离变化，点划线表示安全半径。可以看出两组集群内最小距离一直保持在安全半径以上，集群可以安全飞行。

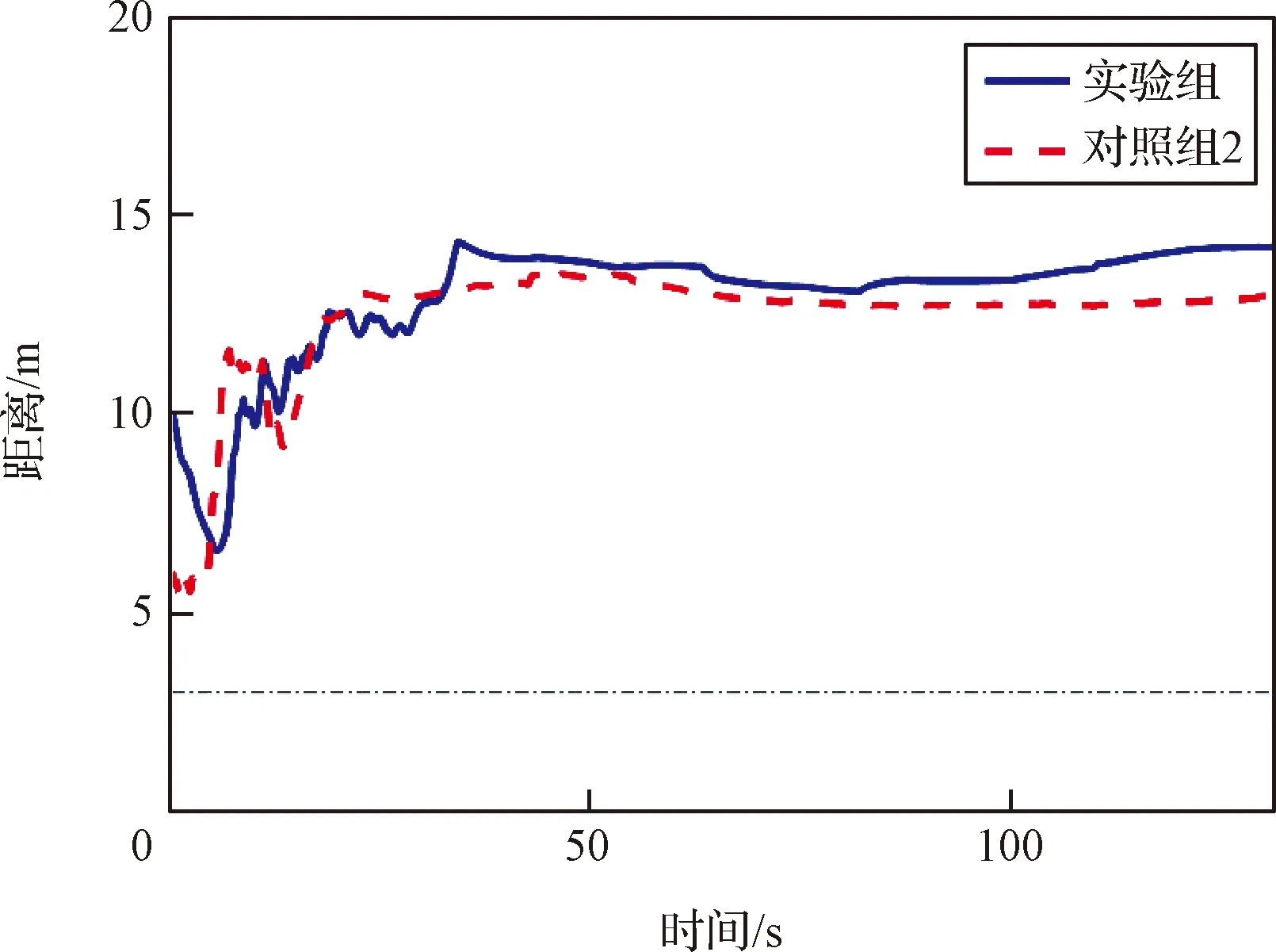
图3 集群中最小距离变化Fig.3 Minimal distance inside the swarm

由于18号无人机参数变化较为剧烈，接下来以该无人机为例，查看具体参数的变化情况。图4～7为两组集群的18号无人机在飞行过程中各项参数变化。图4为18号无人机三轴位置误差变化曲线，实线、虚线和点划线分别表示,和轴方向参数变化。可以看出三轴误差不会收敛到0附近，也不会发散，是因为机间势能使过近的无人机相互排斥，而输入路径只有一条，控制器的一致性部分会起到“吸引”其沿期望路径飞行的作用，二者在一定距离上保持平衡。

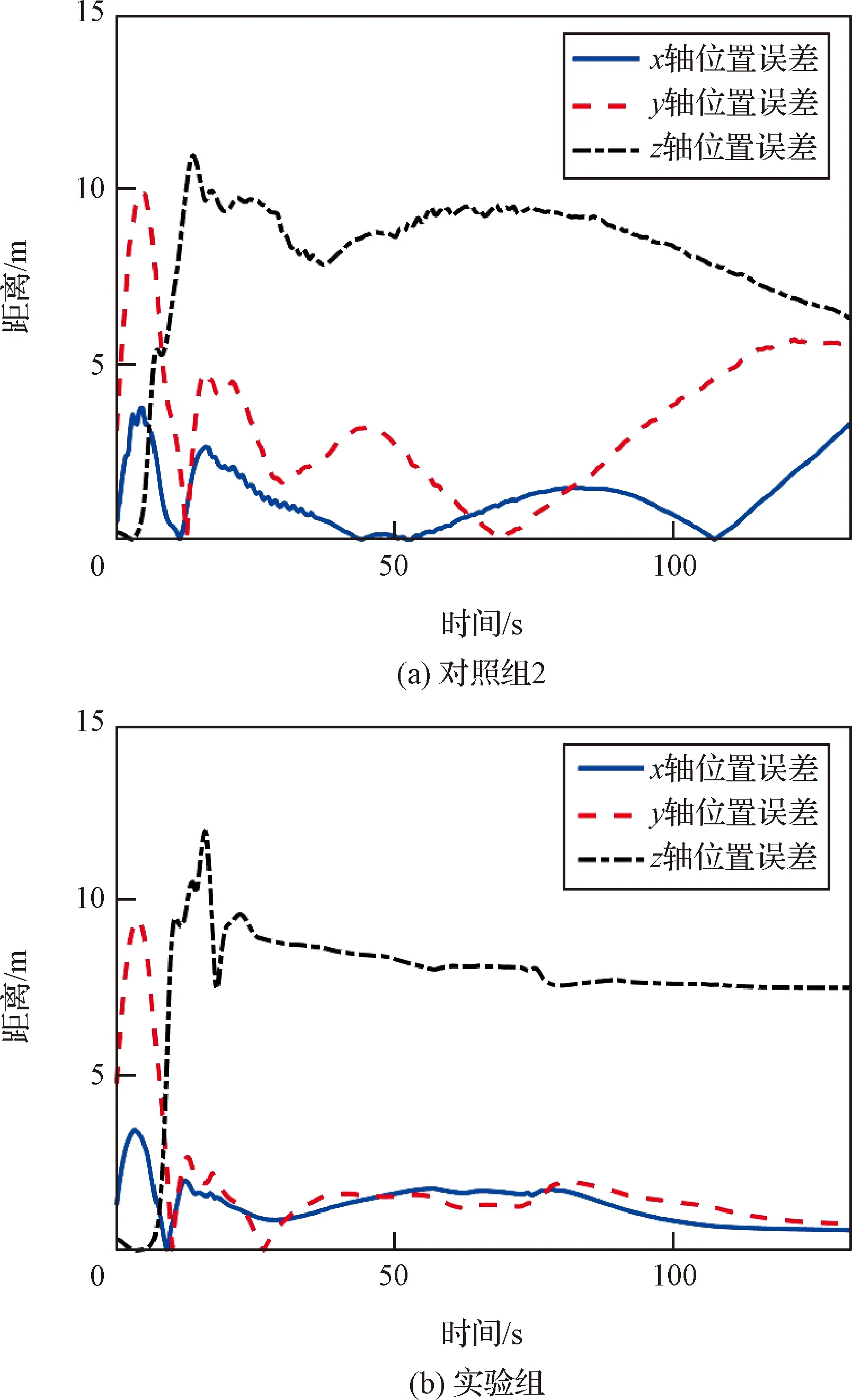
图4 18号无人机三轴位置误差变化曲线Fig.4 Three-axis position error curves of No.18 UAV

图5为18号无人机三轴速度误差变化曲线。可以看出随时间推移速度误差逐渐趋近于0，但稳定后实验组的三轴速度变化稳定，没有抖振，而对照组2的三轴速度仍有明显的抖振现象。

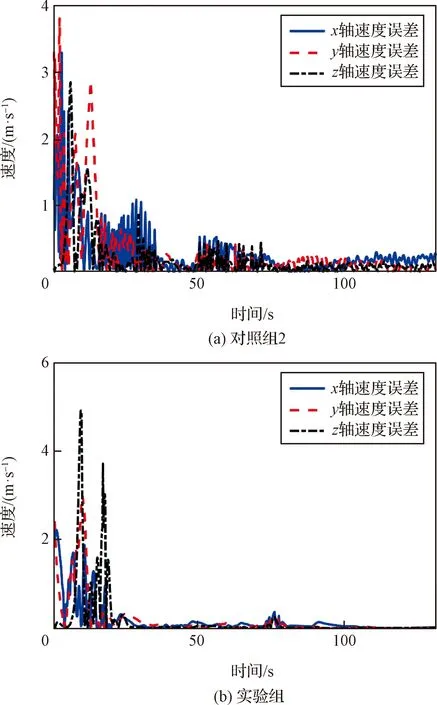
图5 18号无人机三轴速度误差变化曲线Fig.5 Three-axis velocity error curves of No.18 UAV

图6为两组集群中18号无人机水平速度、偏航角速度和竖直速度的变化曲线，其中虚线和实线分别表示对照组2和实验组相应参数变化，点划线为两组集群根据无人机约束式(2)得到的上下限，分别为水平速度约束、偏航角速度约束和竖直速度约束。可以看出在两组集群的飞行仿真过程中，18号无人机一直在满足约束的范围内飞行。

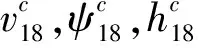
从以上两组集群仿真结果图可以看出,仿真前期许多参数均发生了一定程度的抖动，是因为前期集群在形成稳定相对构型的过程中，机间不断尝试寻找最低的机间势能和最稳定的相对构型，每次抖动均对应了一次局部相对构型的调整。随着时间推移，对照组2在相对构型趋于稳定后仍存在明显的抖振现象，而实验组的各项参数逐渐趋于稳定，并且不存在抖振现象，证明本文提出的自适应通信拓扑对抖振现象具有很好的抑制作用。

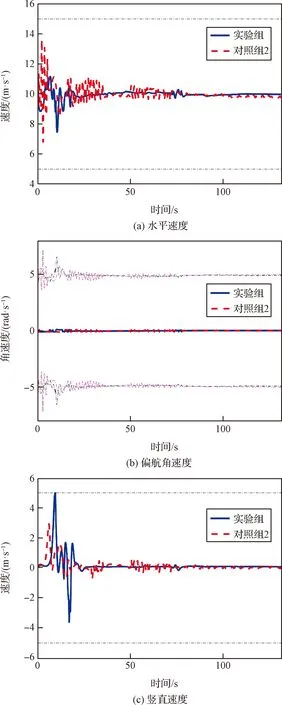
图6 18号无人机水平速度、偏航角速度和竖直速度变化曲线Fig.6 Horizontal speed, yaw speed and vertical speed curves of No.18 UAV

图7 18号无人机控制项变化曲线Fig.7 Control term curves of No.18 UAV

综合两部分仿真校验结果，本文设计的集群协同控制器相较于传统协同控制器，具有输入少、飞行稳定抗抖振的优势。

5 结 论

本文针对无人机集群飞行控制需要规划过多飞行路径的问题，面向集群长途奔袭过程，结合LQR与机间防撞，完成了弱路径约束下的无人机集群协同控制器的设计。控制器采用了仿生的自适应通信拓扑以稳定机间防撞产生的抖振，具有良好的可扩展性，且飞行稳定、资源消耗少。通过设置传统协同控制器作为对照组1和基于距离的通信拓扑作为对照组2，以及基于本文设计的自适应通信拓扑的集群协同控制器作为实验组，比较不同控制器控制下的30架固定翼无人机集群飞行的仿真校验与结果分析，本文设计的分布式控制器可以实现规划一条路径下无人机集群无机间碰撞的飞行，且在自适应通信拓扑下能有效抑制飞行过程中的抖振现象。