小推力最优轨迹协态估计的高效机器学习方法

刘宇航，杨洪伟，李 爽

(南京航空航天大学航天学院，南京 211106)

0 引 言

电推进因其高比冲的特点可以大幅降低燃料消耗，在深空探测任务中具有重要的作用。电推进发动机推力小，持续开机时间长，相应的小推力轨迹优化问题具有强非线性。间接法是求解小推力轨迹优化问题的主要方法之一。在间接法中，因引入的协态变量没有实际物理含义，且取值范围不定，所以协态变量初值猜测问题是间接法主要困难之一。对于燃料最优问题而言，最优控制律为bang-bang控制，这种控制律的不连续性则进一步加剧了协态变量猜测的敏感性,提升了间接法打靶求解时的收敛困难。针对协态变量初值猜测困难问题，Bertrand等提出了平滑技术，即构造优化指标同伦函数，先求解较易的能量最优问题，然后通过同伦参数的改变，逐步同伦到较难求解的燃料最优问题。Jiang等进一步提出了协态变量归一化技术和开关函数检测技术，发展了求解高效的小推力轨迹优化同伦法。潘迅等以及沈红新等利用同伦法分别解决了由中途飞越约束和多圈转移引起的小推力轨迹优化困难，丰富了同伦法的使用场景。为了避免协态初值猜测， Wu等、Yang及其团队分别基于线性化、引力场同伦、推力同伦等方法推导了协态变量初值的近似解析解。此外，也有李鉴等利用无损卡尔曼滤波(UKF)将问题转化，避免了初值猜测的困难。但上述文献研究的小推力轨迹优化方法针对的是定比冲情形。

对于深空探测任务而言，由于电推进发动机功率会随着航天器相对太阳的距离增大而降低，调节比冲可以提供所需的小推力幅值，因此变比冲电推进更具有工程实用性。但是使用变比冲模型会使变量增加，使得轨迹优化产生了新的困难。Taheri则将含双曲正切函数的复合平滑控制方法应用于变比冲发动机模型中。Chi等提出了新的同伦指标函数，解决了传统同伦法求解时存在的控制量耦合困难。Li等进一步研究了双同伦方法。虽然同伦法求解变比冲小推力轨迹优化问题效率很高，但仍需协态变量初值猜测，并且需要同伦迭代，无法直接求解燃料最优问题，不适用于在线轨迹优化。对于深空探测小推力转移过程而言，由于存在各种扰动，探测器会偏离标称轨迹，存在轨迹在线重规划的需求。本文将针对燃料最优变比冲小推力轨迹优化问题，研究无需猜测的协态变量初值快速确定技术，发展具备在线轨迹规划能力的轨迹优化方法。

近年来，人工智能在航天领域的应用备受关注，为解决航天工程问题提供了新思路，在航天动力学与控制领域也已取得了较为丰硕成果。在深空探测轨迹优化与设计方面，基于机器学习的方法可以用于估计转移可达性快速评估、小推力转移剩余质量快速预测、最优轨迹快速规划等。针对深空探测任务中航天器自主性的需求迫切，基于人工智能技术的小推力最优实时制导与控制方法也逐渐被提出。结合间接法理论和人工智能技术，发展小推力轨迹快速优化或者实时制导方法是当前研究的一个主要技术途径。本文研究小推力轨迹快速优化也将以间接法为基础，围绕协态变量初值敏感性这一制约轨迹优化效率的因素，采用机器学习方法建立协态变量与状态量的映射关系，实现协态变量初值的高精度高效估计。

基于机器学习估计协态变量初值时，首先需要生成大量最优轨迹，建立数据集。Yin等提出通过扰动标称最优轨迹参数产生数据集的方法。该方法将标称轨迹的协态变量初值代入扰动后的燃料最优控制问题求解，因考虑的状态量扰动小，故易收敛。但是，当扰动量增大时，标称轨迹与受扰轨迹的协态变量初值偏差将增大，导致求解难以收敛。本文研究拟基于最优轨迹延拓，发展适用于大扰动情形的数据集高效生成方法。同时，也将分析轨迹延拓策略与扰动上限和数据集生成效率的关系。其次，基于机器学习的方法需要设计合理的人工神经网络映射关系。现有的研究中映射输入量往往仅考虑位置速度或者轨道根数的一到两种状态量形式，应用于小推力轨迹优化时收敛率还存在一定的不足。本文将研究多形式状态量组合输入的方法，进一步提升收敛率。此外，本文也将分析人工神经网络结构对求解效率的影响并对其进行优化设计。

1 变比冲小推力轨迹优化问题

1.1 变比冲小推力转移动力学模型

本文假设航天器采用离子电推进发动机，其能量全部来源于太阳能。在太阳引力的作用下，航天器的动力学模型为：

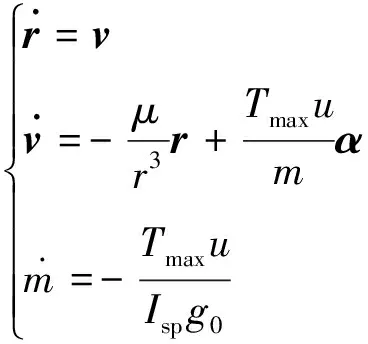
(1)

≤≤

(2)

推力幅值由下式计算得到：

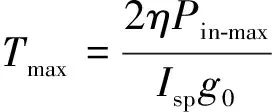
(3)

式中:为发动机输入功率利用效率；为最大输入功率。

在实际航天器工作中，为保证系统功能正常运行，所以由太阳能电池板产生的电能首先供给除发动机外的设备，其次再供给发动机产生推力。而太阳能电池板的输出功率受航天器与太阳距离的影响，具体关系如下:

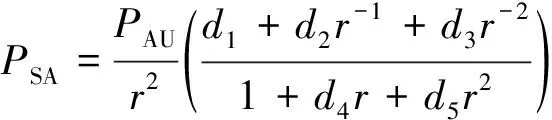
(4)

式中:为太阳能电池板的输出功率；为1个AU距离下太阳能电池板输出功率；括号中的部分代表太阳能板效率随航天器相对太阳的距离改变的经验值。进一步，可以列出发动机的输入功率：

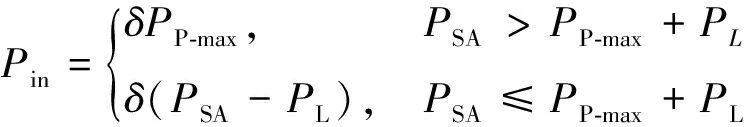
(5)

式中:为发动机输入功率；为发动机功率处理器最大输入功率；为占空比，代表发动机功率处理器真实工作时间与总开机时间的比值；为除发动机系统外其它系统所需总功率。

1.2 小推力轨迹燃料最优控制

首先建立燃料最优控制问题性能指标：

(6)

在求解燃料最优控制问题中,由于最后推导出的最优控制律为bang-bang控制(只取0或1)，所以采用式(6)的性能指标在开关切换点处对状态和协态微分方程积分时不连续，且增加了对于协态变量初值猜测的难度。于是在构造性能指标时采用同伦方法，引入同伦参数,由1逐渐变为0，=0时为燃料最优控制问题。

由于协态变量没有具体的物理含义，在选取协态变量初值时没有明确的猜测范围，极大地影响了求解效率，本文采用文献[5]中提出协态变量归一化的方法，引入归一化协态变量，将包括在内的8个协态变量初值限制到一个8维的单位球面，可极大地提高猜测效率。

由此燃料最优控制问题性能指标改写为：

(7)

进一步，哈密顿函数为：

(8)

式中：，和分别表示位置、速度和质量的协态变量。

根据庞德里亚金极小值原理，若使哈密顿函数取极小值，则·取极小值，此时与方向相反，最优推力方向：

(9)

推导出欧拉-拉格朗日方程为：

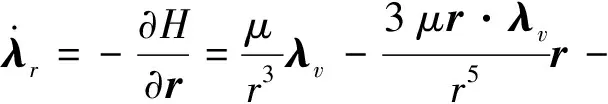
(10)

(11)

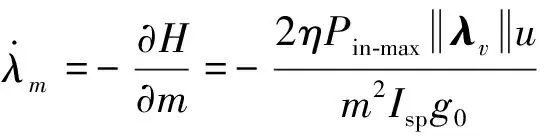
(12)

由于比冲在区间主动变化，则最优比冲大小计算方法为：

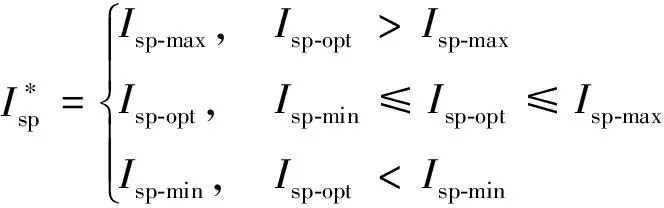
(13)

式中:如下：

(14)

对于采用改进对数同伦函数的式(7)，最优发动机节流度写为：

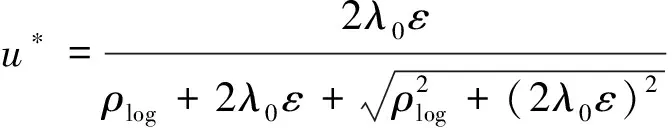
(15)

开关函数：

(16)

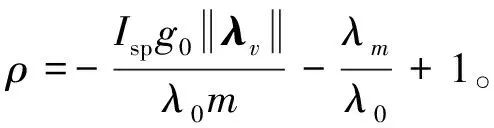
考虑航天器在任务中始末位置速度固定，任务时间固定。末态质量自由，则对应的末态质量的协态变量()=0。打靶方程为：

(17)

式中:≜[,,,]。

至此，将燃料最优控制问题转化为两点边值问题，满足打靶方程的情况下，将状态初值和协态变量初值代入运动微分方程(式(1))、协态微分方程(式(10)～(12))中即可得到燃料最优控制问题的最优解。所以，协态变量初值的猜测对于问题求解十分重要，本文介绍一种基于机器学习进行协态变量初值估计的方法。

1.3 求解方法简述

本文采用间接法解决小推力轨迹优化问题。间接法是将小推力问题作为最优控制问题，首先给定一个性能指标,引入协态变量,构造哈密顿函数，根据最优性的一阶必要条件推导出状态变量和协态变量的微分方程和最优控制律。此时将最优控制问题转换为两点边值问题，通过打靶的形式在满足边界条件下对状态和协态微分方程进行积分，得出小推力控制问题的最优解。

2 基于最优轨迹延拓的数据集高效生成方法

在使用机器学习方法前，需生成大量燃料最优轨迹的数据集，而大量求解燃料最优控制问题会花费大量时间成本。文献[21]中提出了一种最优轨迹快速生成的方法，其原理是给标称轨迹末端状态一个很小的扰动值，将标称轨迹的协态变量初值当作猜测值代入扰动后的燃料最优控制问题中，因扰动量很小，所以标称轨迹的协态变量值接近真实值，猜测很容易收敛。

本文中提出了一种基于最优轨迹延拓的数据集高效生成方法，相比文献[21]的优势在于：扰动量大的情形下也可高效地生成数据，有利于生成空间范围更大的数据集。

以轨道根数作为状态量的轨迹生成为例，基于最优轨迹延拓生成数据集的步骤是：

1)确定新轨迹与标称最优轨迹不同的状态量，可以是末状态不同，也可以是初状态不同。以初状态不同为例，新轨迹的初始状态记为(+Δ,+Δ,+Δ,,,)，其中(Δ,Δ,Δ)为扰动量。

2)设定扰动上限(Δ,Δ,Δ)，使扰动量(Δ,Δ,Δ)在不超过扰动上限的范围内随机选取。

3)将扰动量划分为次达到，相邻两次扰动量之差为(Δ,Δ,Δ)。每一次增大扰动量时，都计算当前扰动量下的最优轨迹，逐渐增加扰动量，直至达到设定的扰动量(Δ,Δ,Δ)。此时，计算了条不同轨迹，且他们初始状态之间的差值都是线性关系。

值得注意的是，在每一次迭代中协态变量的猜测值都采用上一次得到的协态变量初值，当上一次迭代中没有收敛，则使用上一次的猜测值。虽然总扰动量(Δ,Δ,Δ)很大，但是每两代间的扰动量(Δ,Δ,Δ)较小，所以猜测很容易收敛。基于最优轨迹延拓数据集生成方法的算法逻辑如图1。产生数据集的效率及数据集的空间范围受到总扰动量(Δ,Δ,Δ)和延拓次数的影响，需要选择合适值。

3 基于机器学习的协态变量初值估计

3.1 人工神经网络

人工神经网络(ANN)由输入层、隐含层和输出层构成，其原理是通过许多人工神经元组合构造出输入和输出的映射关系，人工神经网络可以用于具有非线性的问题中，原理上来说可以构造任意输入输出的映射关系。人工神经元机理类似于生物神经元，是将输入加以权重和偏置，通过激活函数将此加入权重和偏置的输入值映射为输出值。训练人工神经网络的过程就是不断迭代优化人工神经元中权重和偏置的值，使得指标函数最小，如均方差(MSE)函数。本文中神经网络的训练采用反向传播算法(BP算法)。

图1 基于最优轨迹延拓数据生成算法Fig.1 Data generation algorithm based on optimal trajectory continuation

3.2 超参数的选择

超参数的选择会直接影响训练效果，选择合适的超参数是必要的。主要确定的超参数有：激活函数、神经元数量、隐含层层数、学习率等。在本文中，激活函数使用双曲正切S型函数，学习率设置为0.001，神经元数量、隐含层层数的选取将在4.3节中给出。

4 神经网络训练与分析

4.1 仿真参数设定

使用Fortran语言编写最优轨迹生成程序并通过MATLAB神经网络工具箱进行训练，硬件使用Intel i7-8700K的CPU，主频3.70 GHz。

本文以结束任务前500天的时刻进行重优化为例，校验最优轨迹延拓数据生成法以及人工神经网络在估计协态变量初值的效果。

在本文中扰动轨道根数以产生数据集，动力学方程仍在笛卡尔坐标系下建立。标称轨迹的初末状态及协态变量初值见表1～2。

表1 初末状态Table 1 Initial and final state values

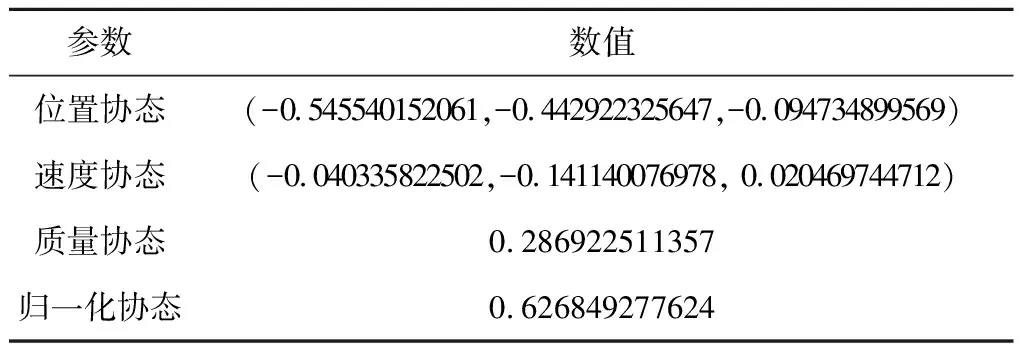
表2 协态变量初值Table 2 Initial values of co-state variables

4.2 扰动上限对轨迹生成效率影响

本文中扰动后的轨迹将以与标称轨迹不同的初始状态到达与标称轨迹相同的结束状态。以计算10000次为例，比较延拓次数为1、10和100时所需时间和成功率，=1时对应为直接扰动方法，即文献[21]中所述方法。在表3中，扰动编号从A到F扰动上限依次增大，具体扰动大小从0至扰动上限值中随机选取。

由图2可以看出，随着扰动上限的增大，三种方法生成最优解的个数都会降低。在扰动上限大小相

表3 扰动上限设定Table 3 Set of different upper limits of the perturbation

图2 生成轨迹个数随扰动上限变化曲线Fig.2 The number of generated trajectories with respect to the upper limit of the perturbation

图3 计算时间随扰动上限变化曲线Fig.3 Calculation time varies with the upper limit of the perturbation

同的情况下，生成最优解个数由高到低依次为：延拓100次、延拓10次、直接扰动。由图3可以看出,延拓100次的方法比直接扰动方法计算10000次所需时间更短。当扰动上限为F时，直接扰动用时大量减少，其原因是成功生成解的个数特别少，所以少了很多积分求解轨迹的时间，总时间相较E时下降较多。

综上，可以看出基于最优轨迹延拓相比于直接扰动成功率更高，计算速度更快，尤其是在扰动量较大时更为明显。而且，延拓次数的增大会提高生成最优轨迹的效率。经计算，在扰动编号D条件下，延拓100次比直接扰动成功生成最优解速度快4.9倍；在扰动编号E条件下，快7.7倍；在扰动编号F条件下，快15.8倍。

4.3 神经网络训练

本文使用50万的数据集进行训练，另取2万组数据作为样本用于误差分析。考虑到设定的扰动上限尽可能与实际可达到扰动上限接近，并尽量使扰动上限取较大值。最终，数据集生成时设定扰动上限为扰动编号E对应的值，并使用延拓次数为100次的基于最优轨迹延拓方法生成数据集。最后求得50万组数据的实际扰动上限见表4。

表4 实际扰动上限Table 4 Actual upper limit of perturbation

为对比不同输入对于协态变量初值猜测效果的影响，本文分别将速度位置、轨道根数、改进春分点轨道根数作为ANN的输入；将位置协态初值、速度协态初值、质量协态初值、归一化协态初值作为ANN的输出，共8维输出。三种ANN不同输入的方法中，只将由半长轴、偏心率和轨道倾角引起改变的量作为ANN的输入。在进行神经网络训练前，对所有的输入量进行归一化处理。

1)方法一：速度位置作输入

采用速度位置作为输入时，速度和位置各有三个维度，共有六个量作为ANN的输入。

2)方法二：轨道根数作输入

采用轨道根数作为ANN的输入时，输入为半长轴、偏心率、轨道倾角三个量。

3)方法三：改进春分点轨道根数作输入

采用春分点轨道根数作为ANN的输入时，输入为除外的其余五个改进春分点轨道根数元素。其中，=++，，和分别表示航天器的真近点角、近地点幅角和升交点赤经。

式(18)和式(19)分别为平均相对误差和标准偏差的计算公式。表5～10中给出了三种输入下不同神经元数量和隐含层层数不同时平均相对误差(%)和标准偏差(×10)大小。

(18)

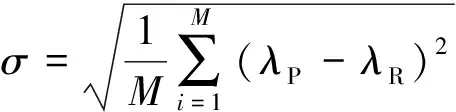
(19)

表5 平均相对误差(方法一)Table 5 Average relative error (Method 1)

表6 标准偏差(方法一)Table 6 Standard deviation (Method 1)

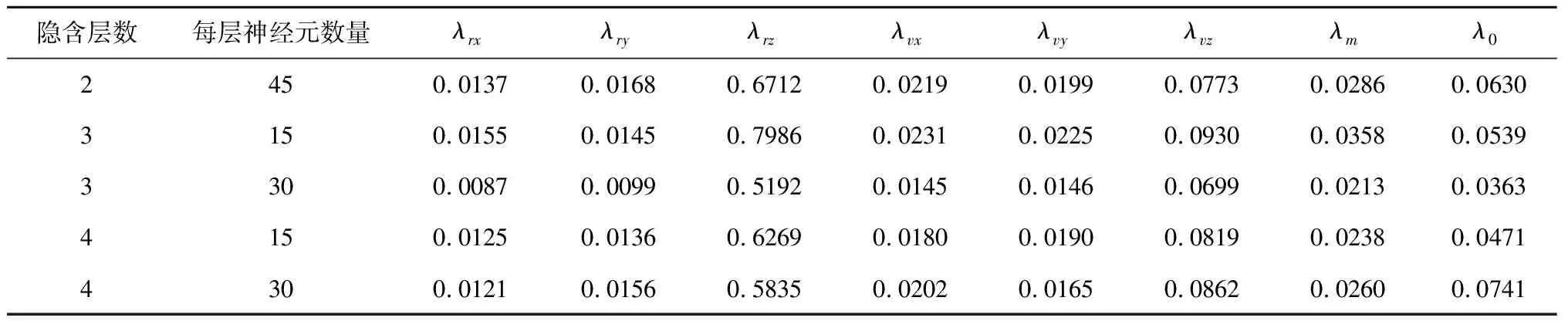
表7 平均相对误差(方法二)Table 7 Average relative error (Method 2)

表8 标准偏差(方法二)Table 8 Standard deviation (Method 2)

表9 平均相对误差(方法三)Table 9 Average relative error (Method 3)

表10 标准偏差(方法三)Table 10 Standard deviation (Method 3)

式中:为样本数；为神经网络预测的协态变量初值；为真实的协态变量初值。

在列举的五种神经网络结构中选取平均相对误差和标准偏差总体较小的网络结构。最终确定：当输入为位置速度时，采用4层隐含层，每层15个神经元的结构；当输入为轨道根数和改进春分点轨道根数时，采用3层隐含层，每层30个神经元的结构。

4.4 协态估计效果分析

在50万的训练数据外选取2万数据，用于测试人工神经网络初值估计的效果。

表11中给出了三种不同输入形式训练的ANN用于初值估计时最优控制问题的求解收敛率。神经网络输入为改进春分点轨道根数时收敛率最高，但是三种ANN模型求解收敛率相差不大，均在95.00%左右。经计算，同伦法随机猜测一次的计算收敛率为70.00%，远低于本文中方法。为了进一步提高收敛率，将三种不同输入形式的ANN结合，选定其中一个神经网络作为主输出，当此神经网络所估计值求解不收敛时，使用其他两种输入的ANN重新估计，这样可以将求解收敛率提高到99.78%，算法流程见图4。图5为对于2万测试数据，三种不同输入形式的ANN结合所成功求解出的轨迹。

对2万个样本中成功收敛部分的计算时间进行统计。采用ANN估计的协态初值进行轨迹优化的时间消耗分为两部分：神经网络协态估计用时和轨迹优化用时。经计算，采用方法一至方法三的平均时间分别为0.02794 s、0.02722 s和0.02678 s；使用传统同伦方法的求解平均用时约为0.38770 s，本文方法比传统同伦方法约快13.88倍。

表11 ANN协态初值估计求解的收敛率Table 11 The convergence rate of estimating the initial values of co-state variables using ANN

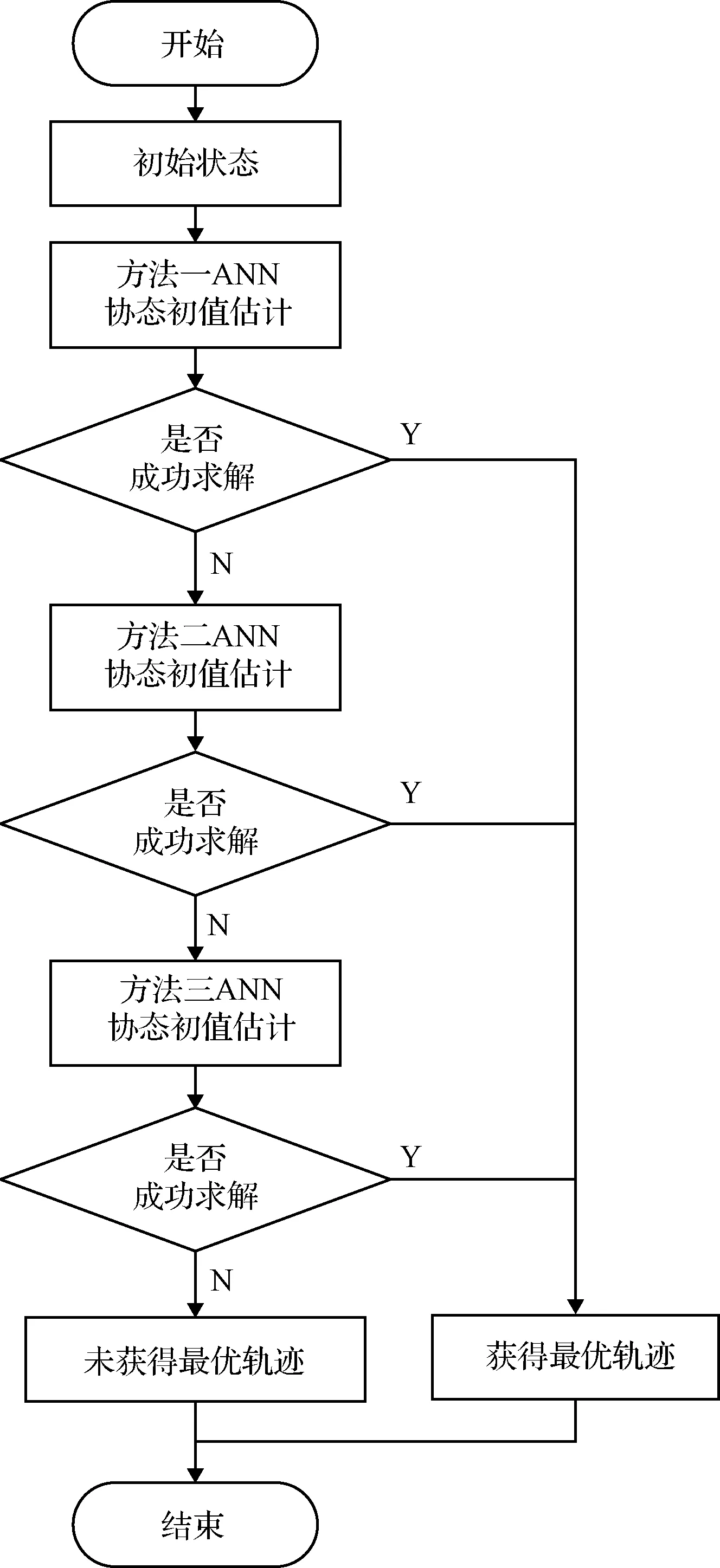
图4 基于组合输入的ANN求解最优轨迹算法Fig.4 ANN algorithm for solving the optimal trajectory based on the combined inputs

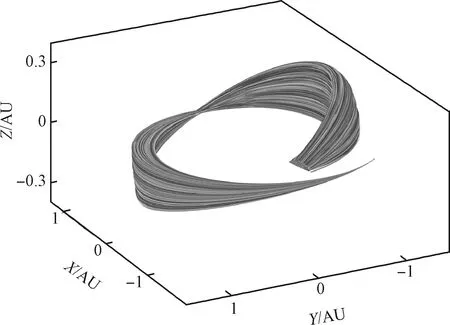
图5 求解成功轨迹图Fig.5 Successfully solved trajectories

5 结 论

本文针对变比冲小推力轨迹间接优化中协态变量初值猜测困难的问题，提出一种基于机器学习进行协态初值高效高精度估计的方法。在最优轨迹生成中，随着扰动上限增大，求解效率会明显下降。为了提高求解效率，提出了基于最优轨迹延拓的数据集生成方法。本文提出的数据集生成方法在高扰动上限情况下可以将数据集生成速度提升几倍甚至十几倍。并构建了基于位置速度、轨道根数和改进春分点轨道根数多形式状态量组合输入的人工神经网络。多形式状态量组合输入可以将求解收敛率提高到99.78%。此外，轨迹求解的平均总用时仅为0.02700 s左右。仿真结果表明，采用本文方法可以高精度、高效地估计协态变量初值，本文方法可用于燃料最优变比冲小推力在线轨迹优化设计。