差分组合模型在BDS卫星钟差预测中的应用

王建敏，李 特，吕 楠，冯 源

（辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000）

0 引言

全球卫星导航系统（global navigation satellite system, GNSS）是一种基于卫星星座的空基无线电导航定位系统，其建立和应用是世界大国的高精技术竞争的重点之一。为建设世界一流的卫星导航系统，更好地为全球用户提供可靠有效的基础服务，我国于1994年开始自主研发北斗卫星导航系统（BeiDou navigation satellite system, BDS），截止到2020年6月23日，北斗三号全球卫星导航系统即北斗三号（BeiDou-3 navigation satellite system, BDS-3）最后一颗全球组网卫星在西昌卫星发射中心点火升空，至此北斗三号基本全部建成。作为一种基于时间测量的系统，BDS导航定位等服务精度和实时性均受到时间精度的影响，而卫星钟差获取的滞后性，对BDS的应用造成了较大影响，因此，利用卫星钟差数据建模并进行预报，具有非常重要的意义和价值。

目前，国内外学者提出了多种钟差预测方法和模型，如二次多项式模型、灰色模型、自回归滑动平均模型、神经网络模型及卡尔曼滤波模型等。文献[7]采用求和自回归滑动平均（autoregressive integrated move average, ARIMA）模型对卫星钟差建模预报，同时，利用动态精密单点定位分析确定最优建模时长和最优预报时长，得到ARIMA模型在 GNSS钟差短期预报中，精度可达 2.5 ns以下的结论。文献[8]将遗忘因子最小二乘法和系数优化因子引入灰色模型（gray model, GM）中，构成PGM（1,1）模型，有效提高了模型在钟差预测中的自适应能力。文献[9]将限制幅度值和预测惩罚机制加入反向传播（back propagation, BP）神经网络模型，提高了氢原子钟的钟差预测精度。文献[10]采用指数平滑法对精密钟差进行预报，实现了少数据建模高精度预报的目的。

然而，以上钟差研究多数以全球定位系统（global positioning system, GPS）数据为实验基础，对BDS卫星钟差预测的研究相对较少；此外，现有的研究在进行GPS卫星钟差预报时，时长大多为中长期并且模型易受数据自身特性影响，如ARIMA模型要求序列为稳定序列，对钟差数据质量要求过高；灰色模型仅适用于预测少量数据，使得误差积累严重。

为解决上述问题，更好地为导航定位授时等服务提供数据支持，本文结合BDS卫星钟特点，在进行数据预处理的基础上，对灰色模型、广义回归神经网络模型和组合模型短期预报情况进行对比分析实验，探讨BDS卫星钟差预测方法，并对其预测精度进行比较分析。

1 单一预测模型

1.1 径向基神经网络模型

径向基函数（radial basis function, RBF）是在解决多维空间插值时被提出的标量函数。1988年，文献[11-12]在生物神经元局部响应原理基础上，将RBF与神经网络结合，由此形成了RBF神经网络。RBF神经网络通过映射关系，将输入数据转至隐含层空间，在由基函数所构成的空间中，对输入数据进行非线性变换，然后将隐含层神经单元进行加权组合，最后结果由输出层输出。

在RBF神经网络中，需要训练的参数有隐含层中基函数的标准差，隐含层中基函数的中心和隐含层与输出层的权值。同时，为保证网络训练的稳定性，RBF核函数一般选取高斯函数，具体形式为

式中：(−c)为高斯函数输出，为网络隐含层节点数；x为输入向量；c为激活函数中心向量；为方差；e为自然常数。

基于RBF神经网络的钟差预测方法，具体流程如下：

1）计算隐含层中基函数中心。对输入钟差序列进行分类，计算个随机钟差样本与其他样本的欧式距离，将距离相近的样本组成集合，计算各个集合的平均值，当平均值与预计中心样本值相同时，则该样本被认为是基函数的中心，若不相同，需重新分类并重复上述计算，直至二者相同。

2）计算隐含层中基函数的标准差。为防止RBF出现太尖或太平的情况，计算标准差的公式为

式中，是所选中心最大距离。

3）采用最小二乘法计算隐含层与输出层间的连接权值，即

式中：w为隐含层与输出层之间的权值；为中心向量的最大值。

4）计算RBF神经网络的输出钟差，即

1.2 广义回归神经网络模型

广义回归神经网络（general regression neural network, GRNN）是建立在非参数回归的基础上，以最大概率为原则计算网络输出的神经网络。与RBF神经网络相比，GRNN的结构更为复杂，由四层组成，分别为输入层、隐含层、加和层和输出层。其隐含层为RBF层，神经元个数与训练的良性样本个数一致，基函数采用高斯函数，表达式见式（1）。基于GRNN模型预测钟差，具体流程如下：

1）输入个钟差数据的学习样本x，将其传递给隐含层。

2）隐含层神经元个数与钟差学习样本数据个数一致。神经元的输出量用输入与对应样本的欧式距离的平方指数形式表示，即

式中：()为隐含层输出；为对应样本；X为第个神经元的输入钟差；为平滑因子。

3）隐含层输出钟差流入加和层，两类神经元进行代数求和与加权求和，其表达式为

式中：S为代数和输出；S为加权和输出；y为神经元间权值。

4）利用加和层数据计算钟差输出值，即

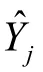
2 组合预测模型

由于单一预测模型预测误差较大且预测数据发散，故将多个单一模型进行线性组合，为消除单一预测模型残差序列中数值小且绝对值大对组合过程中所造成的影响，组合模型的指标为最小绝对值残差。组合模型的表达式为

式中：()为组合模型预测序列；()为构成组合模型的单一模型的预测序列；,,…,k为单一模型权重；是单一模型的个数。

在钟差预测中，将预处理后的钟差序列{x}进行一次差分得到差分序列{}，分别采用 RBF神经网络模型和 GRNN模型对钟差差分数据建模预报，然后对单一模型预测数据作差分重构，最后通过基于最小残差绝对值法对钟差预测结果进行组合，其表达式为

式中：()为组合模型预测钟差值；()为RBF神经网络模型预测钟差值；()为GRNN模型预测钟差值；、为系数。当RBF神经网络模型残差绝对值大于 GRNN模型时，取值为 0，取值为 1；当 RBF神经网络模型残差绝对值小于GRNN模型时，取值为1，取值为0；当两个模型残差绝对值相同时，、为任意实数且∈ [ 0,1]，∈ [ 0,1]，+= 1。图1为组合模型的预报流程图。

图1 组合模型预报流程

3 实验结果与分析

3.1 实验数据

为验证组合模型在钟差短期预测中的可行性，采用 2019-09-13 T 05:00:00—2019-09-14 T 05:00:00共24 h的BDS精密卫星钟差作为实验数据，其中前12 h作为建模数据，后12 h作为验证数据。限于文章篇幅，本文仅对C26、C28、C29、C30卫星预测结果进行详细阐述。

3.2 实验方案

1）分别采用GRNN模型、GM（1,1）模型和组合模型预测时长为6 h的钟差数据。

2）分别采用GRNN模型、GM（1,1）模型和组合模型预测时长为12 h的钟差数据。

3.3 数据预处理

由于卫星钟差的原始数据不同于常规时间序列数据，其隶属于相位数据，粗差往往隐藏于钟差序列中，粗差的存在将降低卫星钟预测的精度，因此本文采用中位数法进行粗差探测，具体公式为

式中：为历元个数；为相位数据；y为频率数据；Δ为采样间隔；median为中位数运算符；为频率数据序列的中位数；为正整数；为频率序列偏差绝对值的中位数。

由式（12）可知，当频率数据的绝对值小时，该数据为正常数据；当频率数据的绝对值大时，该数据被定义为粗差。故建模前需对粗差频率数据进行剔除，同时为保证数据完整性，采用分段线性插值法补齐频率数据，本文以C26和C28为例，结果如图2、图3所示。

图2 C26频率数据

图3 C28频率数据

从图2、图3可以得出，中位数法可以将粗差从正常数据中分离，能够达到粗差探测的目的。在粗差探测有效的基础上，确定原始钟差序列中粗差的历元位置，并利用分段线性插值补齐数据，从而保证钟差序列的完整性。

3.4 实验结果与精度评定

采用方案1与方案2对12 h采样率5 min的钟差数据建模，预测接下来6 h、12 h的钟差。本文采用残差绝对值（residual absolute value, RAV）和均方根误差（root mean square, RMS）作为评定模型的精度指标，其计算公式为

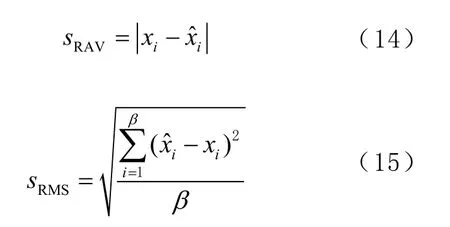
式中：x为钟差真实数据；ˆ为钟差预测数据；为历元个数。实验结果如图4至图11，表1、表2所示。

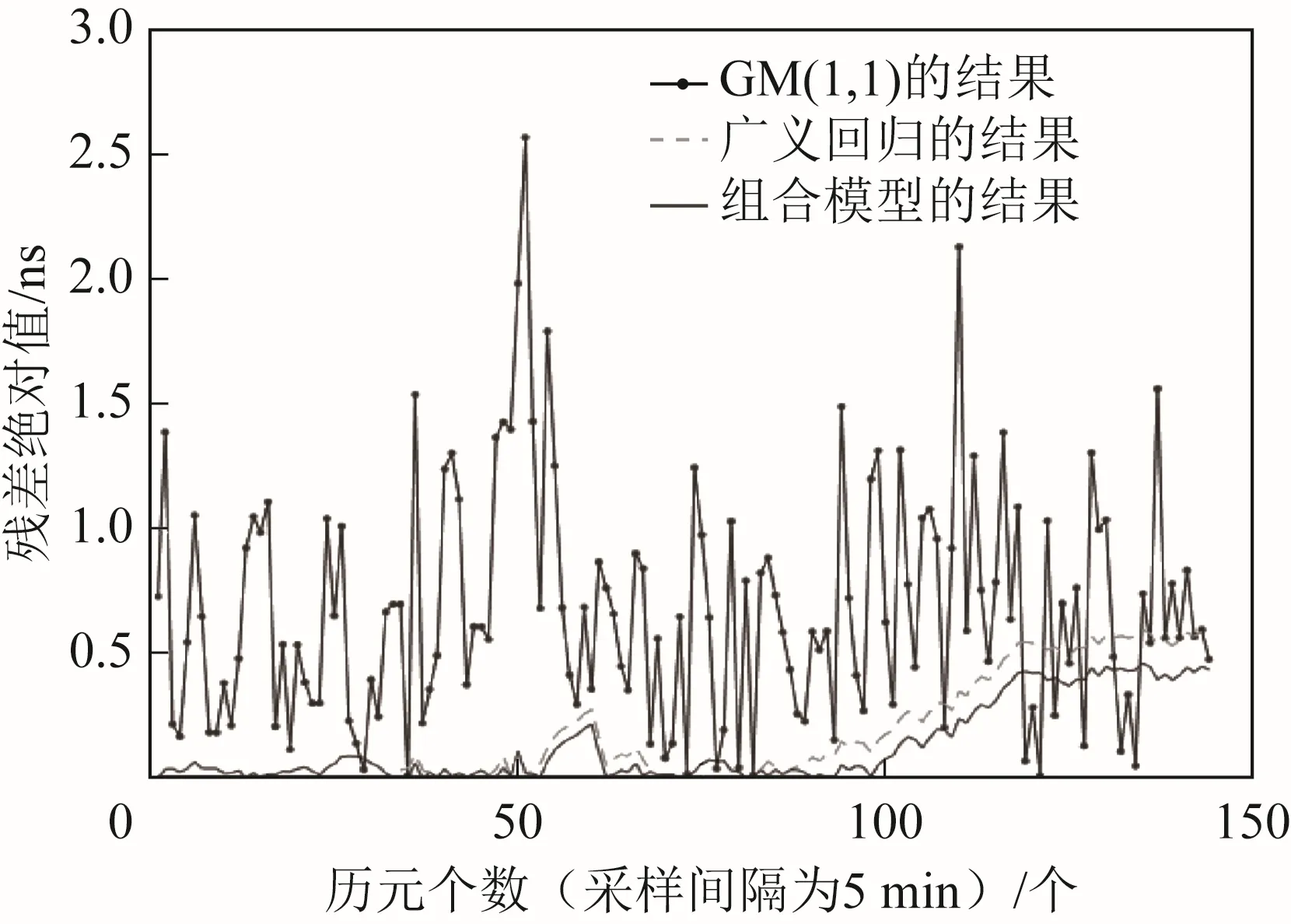
图4 C26残差绝对值

图5 C26均方根值

通过图4至图11、表1及表2可知：

表1 BDS精密卫星钟差残差绝对值预报结果

表2 BDS精密卫星钟差均方根值预报结果

图11 C30均方根值

1）GRNN模型、GM（1,1）模型和组合模型均可应用于BDS精密卫星钟差短期预测，组合模型预测精度优于GM（1,1）模型和GRNN模型。其中 C29的单一模型预报精度较差，但组合模型精度仍达到亚纳秒级，具有较好的稳健性。除C29以外，两种模型预报精度都达到了亚纳秒级。随着预测时长的增加，预测误差均随之增加，但组合模型采用最小绝对值残差的方式，有效降低了误差增量，使得组合模型的误差增量远小于单一模型，且预测数据平滑，稳定性强。

图6 C28残差绝对值

图7 C28均方根值

图8 C29残差绝对值

图9 C29均方根值

图10 C30残差绝对值

2）历元个数与预报精度呈现正相关，随着历元个数增大，预报误差也逐渐增大。GM（1，1）模型受历元个数的影响最大，误差波动明显，GRNN模型受历元个数影响次之，而组合模型稳定最优，历元个数增大后，误差无明显变化。对比单一模型，在残差绝对值的精度指标下，在预报时长为 6 h时，组合模型的平均预测精度的分别提高了 22.39%和 92.56%；当预报时长为 12 h时，组合模型的平均预测精度的分别提高了91.37%和87.80%。在均方根值的精度指标下，当预报时长为6 h时，组合模型的预测精度的分别提高了37.75%和52.27%；当预报时长为12 h时，组合模型的平均预测精度的分别提高了 90.19%和67.11%。

3）在卫星钟差6 h和12 h的预报中，GM（1,1）模型的预测精度最差，平均预报精度在 1.5 ns以上，且数据具有较大的波动性，在4 h左右误差达到最大，模型稳定性差。在 GRNN模型与组合模型的预测结果中，残差绝对值和均方根误差均随着历元个数的增加而增加，且误差增加幅度远小于 GM（1,1）模型，除 C29卫星外，预测时长在0~5 h时，组合模型受 GRNN模型影响较大，故GRNN模型与组合模型预测误差相差不大，但在5 h之后，组合模型受RBF模型影响较大，故组合模型误差增加幅度小于 GRNN模型，且组合模型的模型稳定性好，预报精度明显优于单一模型，在预报时长为6 h时，误差在0.5 ns以内，当预报时长为12 h时，误差在0.6 ns以内。

4 结束语

为解决钟差预测单一模型预报精度低、适应性差等问题，本文提出基于最小残差绝对值的差分组合预测模型，该组合模型将RBF神经网络和广义回归神经网络有效结合，提高了模型的适应性。同时，在钟差建模之前，通过对数据进行数据预处理，剔除粗差数据并用分段线性插值法对数据进行补齐，以保证数据的完整性。最后，模型采用差分钟差数据作为建模数据，提高了数据的稳定性。实验结果表明，相比灰色模型和广义回归神经网络模型，差分组合模型在钟差预测中具有较大的优越性和适应性，且模型预测精准度更高。