导航有线信道特性自适应激励测量学习方法

李蓬蓬，肖志斌，王峰毅，刘 欢，吕志成

（国防科技大学 电子科学学院, 长沙 410000）

0 引言

导航信道模拟器主要用于星地之间、星间的射频链路模拟测试，仿真信号传输复杂的宽带无线信道特性，重现导航卫星射频信号在星地和星间传播环境中的各种延迟、传输衰落、多普勒频移以及多径效应等。在真实导航定位环境中，卫星信号经过功放和窄波束天线的高增益后，发射进入空间环境，地面接收设备需要由天线接收信号，经由低噪放大等环节后解算定位。上述功放、发射天线、接收天线等有线环节，都只涉及信号功率层面的变化，与导航定位信息解算基本无关，在信号测试层面的有线环境搭建中，一般都予以省略。若直接将卫星射频信号经过导航卫星信道模拟器，由接收机接收解算定位，这样也可以避免在有线测试环境中强（卫星天线输出）弱（接收天线输入）信号功率落差过大，测试环境过于复杂难以搭建的问题。因此，需要设计导航信道模拟器在仿真宽带无线信道特性的同时，能够仿真上述有线环节的信道特性。

对于无线信道的测量方法，很多学者进行了研究。文献[6]研究了频域测量法，利用多个频率的激励信号，可以直接获得信道冲击在相应频域的表达，该方法为信道测量的最直接最简单的常用方法，但是其激励信号的频率一般为均匀分布，对于波动剧烈的信道特性无法进行准确测量。传统的无线信道测量方法还包括连续波测量法、扩频滑动相关法等时域测量法，其中连续波测量法在发射端发射固定频率的连续波信号，在接收端测量该频点的功率变换，但是该方法只能应用于大尺度衰落特性的信道测量，无法分辨小尺度衰落。而扩频滑动相关法具有良好的抗干扰性能，但是其伪噪声序列相关计算需要消耗较大的计算时间和计算资源，不适用于快速变化信道特性的实时模拟。文献[9]建立了基于矢量网络分析仪的虚拟大规模多进多出（multiple-in multiple-out，MIMO）信道测量平台，可以实现对大规模MIMO无线信道的自动化测量，但是其应用场景受限，不适用于导航无线信道模拟。

对于功放和天线等有线环节特性测量，文献[10]利用两种不同数学算法进行数据处理，求解待测天线群时延，提高了天线测量精度。文献[11]介绍了利用矢网测量天线时延特性的方法。文献[12]利用幅度差叠加法和有限冲激响应（finite impulse response，FIR）插值法，实现射频功率放大器的时延估计。上述有线环节测量方法都是基于已有设备进行单个实测，对于无法提前预知的有线环节信道特性，无法实现实时快速模拟，因此需要对有线环节进行自适应性测量。

目前国内外针对自适应信道测量的算法研究较少，文献[13]提出了自适应匹配追踪算法进行联合信道估计，其主要适用于免调度非正交多址接入系统，并不适用于导航信道中有线环节测量。文献[14]提出基于压缩感知的移动通信信道估计方法，在提高信道重建精度的同时,提升了信道重建速度，但是其应用信道场景为正交频分复用（orthogonal frequency division multiplexing，MIMO-OFDM）信道，对于导航信道体制并不适用。还可以利用目前比较火热的机器学习方法对导航信道进行自适应测量与建模，但是机器学习无法进行信道特性的实时测量，不满足导航信道模拟器的实时需求。

综上所述，为了使导航信道模拟器在仿真宽带无线信道特性的同时，能够仿真有线环节的信道特性，需要在无线信道测量方法的基础上设计信道模拟器，对有线环节进行自适应性测量。本文在频域测量法中、基于均匀激励测量的导航信道特性学习方法的基础上，提出基于自适应激励测量的导航信道特性学习方法。

1 基于均匀激励测量的导航信道特性学习方法

信道模拟器信道特性学习方法的设计是基于对被学习信道进行有限离散点测量的实现，将被学习信道等效为滤波器，假设其频率响应为

式中：()为被学习有线信道的幅频响应；()为被学习有线信道的相频响应；为频率；j为虚数符号。

利用信道模拟器生成组基带多音激励信号，并调制到与被学习信道相对应的射频频率上以后，其信号可以表示为

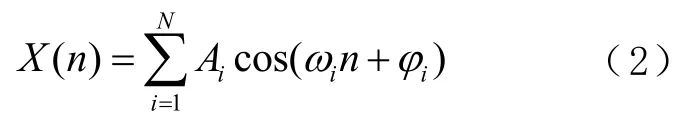
式中：A为第个单音信号的幅度；ϕ为初始相位；为调制后生成信号的第个采样点。

通过射频采集，可以得到经过被学习信道后的多音激励信号()，可以表示为

根据最大似然估计极大似然估计（maximum likelihood estimate, MLE）原理，可以得到采集到的多音测量信号幅度估计的表达式为

相应的相频响应估计表达式为

根据式（4）和式（5）进行解算，可以获得有限个离散点估计值，从而得到被学习信道的幅相特性的离散测量结果。

由于无法提前获取被学习信道的通带波动特性信息，在激励信号产生时，一般采用指定带宽内等频率间隔均匀生成的方式，可以视为对通道特性进行等频率间隔采样。如果通道特性平缓，这种方式性能良好，但是当通道特性存在波动或者趋势变化时，等频率间隔采样就无法尽可能地获取通带特性波动的信息，从而无法反映出待测通道的特性。

本文提出的基于自适应激励测量的导航信道特性学习方法，其主要优点在于，可以基于被学习通道特性变化情况，自适应调整多音激励信号生成的频率间隔，从而有效地获取通道特性变化信息，进而更加准确地学习通道特性。

2 基于自适应激励测量的导航信道特性学习方法

本节以学习通道相频特性测量为例，推导得出自适应激励信号生成方法；利用生成的非均匀多音激励信号测量得到被学习通道特性，最后进行插值拟合，建立被学习信道模型。

针对被学习通道相频特性测量，为了便于观察通带的相频特性变化，一般将之转化为群时延特性，群时延、相位和角频率之间的关系为

式中：()为通道群时延；()为相位；()为角频率。定义群时延波动率为

式（7）中，当多音信号生成呈带宽内均匀分布时，如果连续测量点相等，即特性不发生变化时，群时延变化率为0，此时会出现分母为0的情况，定义此时的群时延波动率为0。

针对被学习通道相频特性测量的自适应激励信号生成方法的流程描述如下：1）利用均匀多音信号激励测量得到等频率间隔群时延特性；2）对通带进行等间隔区间划分，并对各间隔区间进行群时延波动率求和；3）根据求和结果从大到小对间隔区间重新排序，按照排序结果对各间隔区间的采样点个数重新分配；4）利用各间隔区间内新分配的采样点个数，对各间隔区间均匀划分，由此获得整个带宽范围内的非均匀多音激励信号的生成频率。

针对上述流程分析，首先需要给定等间隔区间数，且本文中出现的意义相同。不妨设为取整，则每个间隔区间拥有个采样点，整个通带内的采样点划分为

根据式（7）求出所有群时延估计点的波动率，再求和每一段长度的群时延估计结果的波动率之和，即

根据求得结果，将每一段长度的群时延变化率之和按照大小进行排序，并根据排序结果重新分配各间隔区间内的采样点数。本文采用对整个通带内采样点的群时延波动率之和归一化的方法，来建立测量点数与波动率之间的关系。具体方法如下：

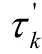
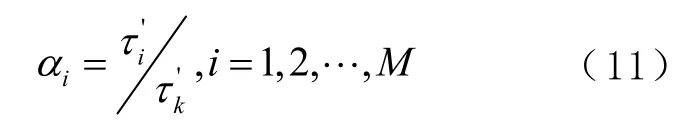
将所有比例因子求和，作为分母进行归一化，由此求得各个区间的采样点数L为

式（12）中L的取值，采用四舍五入取整的方法获得，此时就会出现所有区间内的采样点数总和可能不为的情况。对于上述情况，若采样点数总和多于，则按照间隔区间内采样点重新分配点数从大到小的顺序，依次从各个区间的测量点数中减少 1个，直到所有区间内的测量点数总合等于为止。若采样点数总和少于，则按照间隔区间内采样点重新分配点数从小到大的顺序，依次从各个区间的测量点数中增加 1个，直到所有区间内的测量点数总合等于为止。

利用L对各区间等间隔划分，由此获得通带内所有采样点频率，并根据采样点频率重新生成非均匀多音激励信号，对通道相频特性进行估计与测量。

针对被学习通道幅频特性测量的自适应激励信号生成方法，与相频特性学习方法类似，定义幅度波动率为

式中，为通道幅度。

利用幅度波动率生成非均匀多音激励信号的步骤，与相频特性利用群时延波动率生成非均匀多音激励信号的步骤相同。

利用生成的非均匀多音激励信号测量得到被学习通道非均匀采样点条件下的幅频、相频离散特性，为得到被学习通道模型，需要对其进行插值拟合。考虑到离散通道特性的需求，本文重点关注插值多项式在插值点取值与通道特性测量值的一致性，而不关注测量点导数一致的问题，同时要求在全通带范围内尽量逼近被学习通带的真实特性，也就是要回避插值中的龙格现象。根据插值拟合出的被学习信道特性，进行数字滤波器设计，建立被学习信道模型，用于信道模拟特性添加与测试，此处不是本文重点，这里不做详细叙述。

3 仿真与误差分析

通过基于均匀激励测量和自适应激励测量的导航信道特性学习方法，分别获取被学习通道特性的有限点测量估计值，通过对比两种激励信号生成方法下，插值拟合出的通道特性曲线与被学习通道的真实特性曲线之间的误差，来比较两种激励信号生成方法的优劣。具体仿真与误差分析流程如图1所示。

图1 仿真与误差分析流程

本文以某型号带通滤波器幅度特性为例，利用常用的最小二乘法、三次样条法和分段三次埃尔米特（Hermite）法对两种通道测量方法的拟合插值结果及误差进行对比分析，从而比较两种方法的优劣。

基于均匀激励测量和自适应激励测量的通道特性通过最小二乘法插值拟合后获得的曲线以及与实测通道特性误差如图2所示。

图2 两种激励方法通过最小二乘法的插值拟合结果

图2（a）和图2（b）分别为基于均匀激励测量的通道特性通过最小二乘法插值拟合后获得的曲线以及与实测通道特性误差，图2（c）和图2（d）分别为基于自适应激励测量的通道特性通过最小二乘法插值拟合后获得的曲线以及与实测通道特性误差。

基于均匀激励测量和自适应激励测量的通道特性通过三次样条法插值拟合后获得的曲线以及与实测通道特性误差如图3所示。

图3 两种激励方法通过三次样条法的插值拟合结果

图3（a）和图3（b）分别为基于均匀激励测量的通道特性通过三次样条法插值拟合后获得的曲线以及与实测通道特性误差，图3（c）和图3（d）分别为基于自适应激励测量的通道特性通过三次样条法插值拟合后获得的曲线以及与实测通道特性误差。

基于均匀激励测量和自适应激励测量的通道特性通过分段三次 Hermite法插值拟合后获得的曲线以及与实测通道特性误差如图4所示。

图4 两种激励方法通过分段三次Hermite法的插值拟合结果

图4（a）和图4（b）分别为基于均匀激励测量的通道特性通过分段三次 Hermite法插值拟合后获得的曲线以及与实测通道特性误差，图4（c）和图4（d）分别为基于自适应激励测量的通道特性通过分段三次 Hermite法插值拟合后获得的曲线以及与实测通道特性误差。

从上述三组仿真可以看出，对于三种插值方法而言，基于自适应激励测量的通道测量方法相比于基于均匀激励测量的通道测量方法，其拟合误差较小，对于未知的通道特性其自适应测量效果更好，表1从多种误差分析的角度对学习精确程度进行比较分析。

表1 误差分析

从表1可以看出，本文提出的基于自适应激励测量的导航信道特性学习方法，相比于均匀激励测量，可以更好地学习信道特性，从而实现在导航信道模拟器中建立相应模型，在测试信号中拟合添加被学习信道特性。

4 结束语

针对导航信道模拟器在仿真宽带无线信道特性的同时，还需要能够仿真无法提前预知特性的有线环节的信道特性实际需求，本文提出基于自适应激励测量的导航信道特性学习方法。通过仿真分析可以得出，相比于均匀激励测量，基于自适应激励测量的导航信道特性学习方法能够更加准确地学习信道特性，有助于常用的最小二乘法、三次样条插值法和分段三次 Hermite法进行通道插值的精度提升。