大型Z箍缩装置中心汇流区电感计算
2022-06-10龚振洲魏浩范思源孙凤举邱爱慈
近几十年来,随着电磁驱动内爆的快速发展,国际上积极开展快Z箍缩研究。为了满足Z箍缩在惯性约束聚变、辐射物理、天体物理等领域的研究需求,对Z箍缩装置的功率和电流提出了越来越高的要求。国际上已建或在建的大型Z箍缩装置主要有美国的ZR装置
、中国的10 MA装置
、俄罗斯的Baikal装置
等。
大型Z箍缩装置需要电脉冲传输与汇聚系统(简称为中心汇流区)将空间尺度数十米量级的多路初级脉冲源产生的电脉冲传输汇聚至厘米级尺度的物理负载。中心汇流区通常包括水介质传输线、多层真空绝缘堆、真空圆盘锥磁绝缘传输线(magne-tically insulated transmission line,MITL)、多层柱孔盘旋结构(简称为汇流柱(post-hole convolute,PHC))等,典型的Z箍缩装置中心汇流区如图1所示。中心汇流区参数,特别是中心汇流区电感对Z箍缩装置能量和功率传输效率具有十分重要的影响。为了提高能量和功率传输效率,通常需要尽可能减小中心汇流区电感,然而受绝缘堆耐受电压
、等离子体运动引起MITL间隙闭合
等因素制约,中心汇流区电感不可能无限降低。快速和精确估算中心汇流区电感对大型Z箍缩装置总体设计、电路模拟和参数优化具有重要意义。
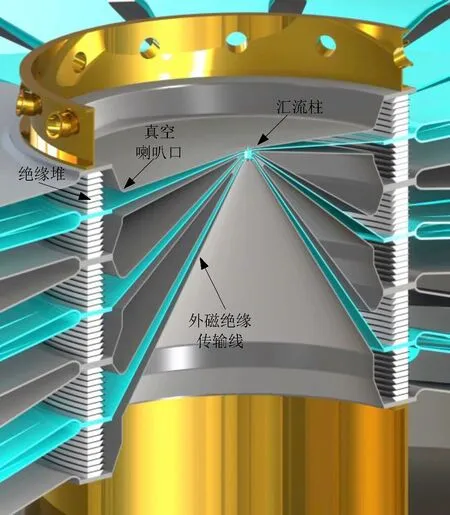
中心汇流区结构复杂,难以直接通过解析方法准确计算电感。三维电磁模拟虽然能够准确计算电感,但存在计算耗时长、计算效率低等问题。美国圣地亚国家实验室的Stygar等给出了中心汇流区电感与绝缘堆电压的定标关系式
,该方法基于美国典型Z箍缩装置中心汇流区电感优化结果,给出了与Z、Saturn相近绝缘堆运行场强下中心汇流区电感最小值,然而当绝缘堆运行场强变化或者中心汇流区结构变化时,就难以应用该式直接给出汇流区电感。中国工程物理研究院的宋盛义推导了圆盘锥真空磁绝缘传输线的真空电感公式
,但忽略了汇流柱电感。汇流柱结构复杂,电感难以直接求解。华北电力大学的倪筹帷等提出了载流细导体的位移电流模型,推导了载流细导体的自感和互感计算公式
。崔翔通过建立载流细导体的传导电流模型,给出了更简化的载流细导体的自感和互感计算公式
。
and is the 2-probe measured resistance, channel length and width for device 1 and device 2, respectively.
本文借鉴上述电感计算方法,对Z箍缩装置中心汇流区几何结构做近似处理,分别给出绝缘堆、真空喇叭口、真空MITL、汇流柱等部件的电感近似计算公式,建立了一种中心汇流区电感快速估算方法,采用三维电磁模拟对计算方法准确性进行了验证。分析了典型结构参数对中心汇流区电感的影响规律,建立了典型Z箍缩装置简化电路模型,实现了从结构参数→电气参数→负载电流的自洽电路模拟。
1 电感计算方法
中心汇流区简化示意如图2所示,图中
为中心汇流区半径。

中心汇流区电感
由以下6部分组成
电感
、
、
、
和
可近似为圆盘结构,电感
、
和
的计算见本文首页OSID码中的开放科学数据。
(1)
式中
、
、
、
、
和
(
)分别表示绝缘堆、真空喇叭段、外MITL、汇流柱、内MITL和负载的电感。
1.1 绝缘堆电感
绝缘堆可近似为径向传输线,所以有

(2)
式中:
为单级FLTD模块内并联支路数;
为单路FLTD初级源模块串联数;
为装置初级源并联路数;
为支路电阻;
为支路电感;
为支路电容。本文取
=23,
=10,
=16,
=50 nF,
=200 nH,
=0.3 Ω。
1.2 真空喇叭口电感
真空喇叭口形状不规则,难以直接求解电感,对其弧形轮廓进行线性等效,如图2所示,所以有

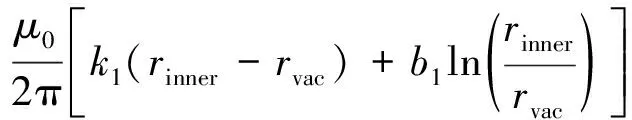
(3)
式中:
和
分别表示以绝缘堆最内侧为坐标原点的真空喇叭口间隙变化的斜率和截距,
=
,
=(
-
)
(
-
);
为真空喇叭口最内侧阴阳极间隙距离;
为真空喇叭口内半径。
1.3 外MITL电感
外MITL如图3所示,分为恒阻抗段
和恒间隙段
。恒阻抗段的真空阻抗不变,随着半径减小,阴阳电极间隙距离逐渐减小;恒间隙段保持阴阳极间隙距离不变,真空阻抗随半径减小迅速增大。
较高的质量是企业在市场竞争中生存下来的关键,质量的提升一直是所有建筑单位共同的努力方向,可从以下方面来提高质量:全面提升施工者的素质,使其形成质量意识,在施工过程中自觉遵守相关规定;清楚规定各个施工环节,并将环节落实到人,改变以往责权不明、推卸责任等现象;若施工时某个环节出现问题,需根据相应的处罚机制,对工作人员进行处理;施工者需要具备灵活变通的能力,对施工现场发生的意外事故,可以迅速做出反应,并解决相关问题[1];管理者可将关于质量把控的内容编写成册,并在施工现场大力宣传;建立切实担负起相关职责,进场材料的质量严格检测,避免不合格材料混入建筑中,从而降低其整体质量。

恒阻抗段
电感有
图9给出了典型
箍缩装置简化电路模型
,主要包括初级脉冲源(等效电容
、电感
和电阻
)、同轴输出水线、整体径向传输线(MRTL)、水喇叭段、中心汇流区和负载等。
=
(4)
式中:
是外MITL恒阻抗段真空阻抗;
=(
-
)
sin(90°-
)是电磁波传输时间,
为恒阻抗段与恒间隙段分界位置半径。
(3) 物面边界: 固壁采用无滑移条件. 由于针对FD-20的实验条件, 有效实验时间只有几十毫秒, 因此采用等温壁面条件Tw=295 K.
恒间隙段
电感有

(5)
式中:
是恒间隙段间隙距离;
是汇流柱的位置半径。
1.4 柱孔盘旋结构和内MITL电感
通常采用柱孔盘旋结构将多层外MITL电流汇聚至内MITL。柱孔盘旋结构电感受汇流柱位置、阳极柱直径、阴极孔形状及尺寸、负载构型等因素影响很大。美国Z装置采用的双层柱孔盘旋结构和内MITL如图4所示,采用12对汇流柱汇流,汇流柱和内MITL电感之和约为3.15 nH
。本文定义距离装置中心半径6~10 cm区域为汇流柱区域,双层柱孔盘旋结构等效电感如图5所示。
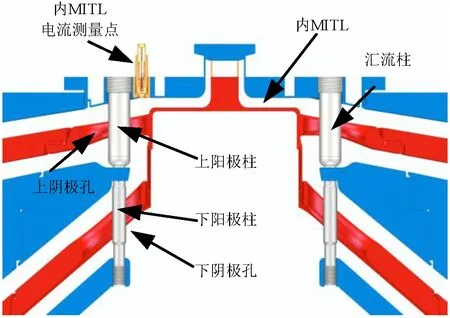

假设电磁波同时到达A、B、C和D这4层MITL,则汇流柱电感
可表示为
={[(
+
)‖
+
]‖
+
}‖
+
当初级脉冲源采用快脉冲直线变压器驱动源(FLTD)时
,等效电阻
、电感
和电容
分别满足
(6)
=
+
+
+
+
+
(
)
本课题依托于水环境治理的时代背景下,选取“河长制”这一具有代表性的政策实践与制度安排为调研对象,基于标准化视角,站在社会公众角度,综合运用多种研究方法,对调研开展后采集的公众看法评价结果与政府客观评议制度成效进行对比,为“河长制”在进一步改革完善中提出对策性建议,以优化其在水环境治理中的效用。
采用本文方法计算中心汇流区总电感,结果约为7
94 nH。表4给出了电感的本文计算值
与三维电磁模型计算值
的对比,表中电感偏差计算方法为(
-
)
×100%。可以看出,总电感
计算偏差为2.2%。
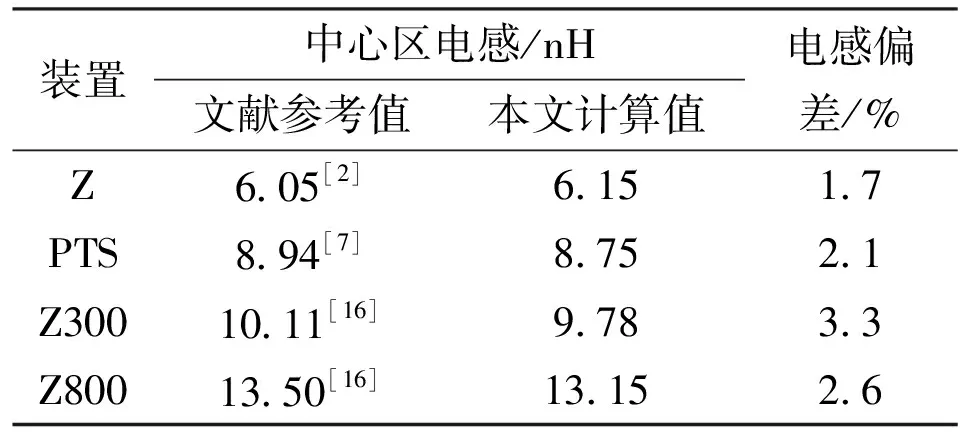
2 电感计算方法准确性验证
采用本文电感计算方法,计算国际上几个典型Z箍缩装置的中心汇流区电感。表1给出了典型Z箍缩装置中心汇流区的参数。表2给出了中心区电感的本文计算值
与文献参考值
的对比,表中中心区电感偏差的计算方法为(
-
)
×100%。可以看出,最大偏差为3.3%。
3 某装置中心汇流区电感计算
以表3给定的某装置中心汇流区参数为例,绝缘堆耐受电压约1.6 MV,中心汇流区半径为1.1 m,绝缘堆由A~D共4层组成,A和B层由5片绝缘环和4片均压环组成,C和D层由6片绝缘环和5片均压环组成,每片绝缘环和均压环厚度分别为3 cm和0.8 cm。整个绝缘堆高度105 cm,4层外MITL真空阻抗分别为2、2、3、3 Ω。柱孔盘旋结构和内MITL结构参数与Z装置相同
。

当给定中心汇流区电气参数(绝缘堆峰值电压
、绝缘堆平均运行场强
)和结构参数(单片绝缘子厚度
、单片均压环厚度
、绝缘堆径向宽度Δ
、真空喇叭段径向宽度Δ
、外MITL真空阻抗
、外MITL恒间隙段距离
、中心汇流区半径
、汇流柱半径
和外MITL上层倾角
)时,通过数值求解式(1)~(6),可获得中心汇流区电感
。
选择低丘缓坡地带、交通方便、土层深厚、具有良好光照条件、水源充足且灌溉方便的笋用林、笋竹两用林;也可对材用林进行定向改造,改造时间一般需要2年。其他林地条件与冬笋型、春笋早出型竹林相同。


4 中心汇流区电感的变化规律
图6给出了绝缘堆径向宽度Δ
、真空喇叭段径向宽度Δ
这两个参数对中心汇流区电感
的影响规律。可以看出,
随Δ
和Δ
增大而增大,且
对Δ
变化更敏感。

中心汇流区电感
随外MITL倾角
的变化如图7所示。可以看出,当外MITL倾斜角度
从0°增大到40°时,中心汇流区总电感
从7.8 nH增长到8.3 nH。虽然
增加不多,但是各层电感差异增大。图7同时给出了中心汇流区柱孔上游的每层电感
、
、
和
(包括绝缘堆和真空喇叭口电感)的变化。最上层的A层电感最小,最下层的D层电感最大。当
=40°时,A层电感为18.5 nH,D层电感为23.6 nH。各层电感差异增大,导致层间电流差异增大,D层绝缘堆电压高、电流小,增加了真空磁绝缘失效的风险。

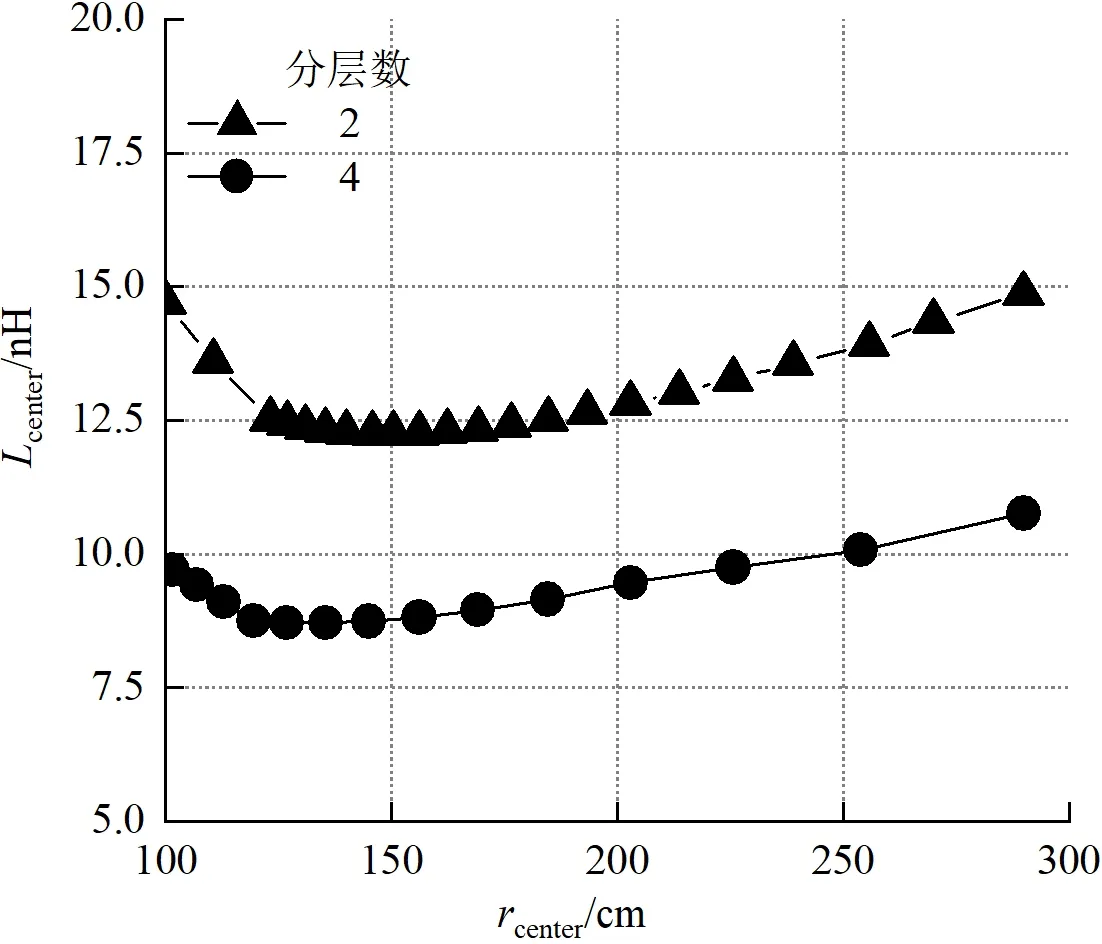
中心汇流区半径和绝缘堆分层数是中心汇流区的重要参数。图8给出了不同分层数下中心汇流区半径
变化对电感
的影响(分层数为2时,汇流柱的电感变化较小,本文忽略其变化)。可以看出,中心汇流区半径相同时,分层数为4时的中心汇流区电感小于分层数为2时的。对于给定的分层数,存在使得中心汇流区电感最小的半径优化值。当分层数为2层、
取1.5 m时,中心汇流区电感最小,为12.2 nH;当分层数为4层、
取1.3 m时,中心汇流区电感最小,为8.5 nH。
5 中心汇流区电感对电流的影响
在涉外婚姻诉讼中,配偶一方可能在另一方配偶起诉之前挑选法院或进行鱼雷诉讼。鉴于此,2005年欧洲共同体委员会在《离婚事项的准据法和管辖权绿皮书》中建议,在例外情形下可以将离婚案件移送至其他成员国法院,如果离婚程序与父母责任诉讼相关联,则需要采取额外的保障措施以确保与《布鲁塞尔条例Ⅱa》第15条的内容相一致[10]10。
前文已获得中心汇流区电感
随分层数、中心汇流区半径等参数的变化规律,因此若能获得MRTL和真空喇叭段参数与分层数、中心汇流区半径的关系,就可以通过电路模拟获得中心汇流区结构参数变化时Z箍缩装置输出参数的变化规律,从而实现了从结构参数→电气参数→负载电流的自洽电路模拟。

杨家溪是一个摄影人不得不来的地方,因为霞浦最出名的一张照片就是出自这里,这也是我此行最期待的拍摄地。杨家溪号称闽东小武夷,亦有海国桃源的美誉,这里的溪水纤尘不染,水质清冽,可乘竹排顺流而下。这里拥有纬度最北的古榕树群和江南最大的纯枫叶林,最值得一提的是一株“榕树王”,树龄已有800多年。大榕树似乎有着灵气,一路上阴雨不断,可当我们抵达这里时,久违的太阳终于露出头来,在烟雾缭绕的环境之中,洒下了漫天的光束。
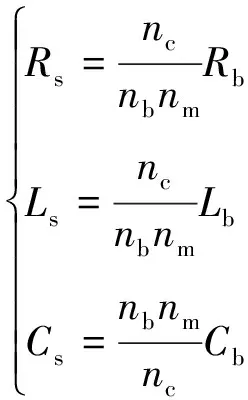
(7)
式中:
为真空磁导率;
为绝缘堆高度;
为绝缘堆外半径;
为绝缘堆内半径。
同轴输出水线特征阻抗、MRTL输入阻抗
通常与初级脉冲源输出阻抗
匹配,由式(8)计算取
为0.066 Ω。MRTL输出阻抗
满足式(9),一般需要保证
>
。
和
的计算式分别为

(8)

(9)
式中:
为相对磁导率;
为真空介电常数;
为相对介电常数;
为分层数;
为整体径向传输线末端阴阳极间隙距离,本文取满足水绝缘要求的最小距离。
水喇叭段入口阻抗等于MRTL出口阻抗,水喇叭段出口阻抗等于绝缘堆入口阻抗
,绝缘堆入口阻抗
满足
秦淮河流域地势周围高中间低,为一完整的山间盆地。上游水系支流多,中游河床开阔,下游与南京护城河合一,自东向西横贯市区南部至西水关流出南京汇入长江。

(10)
本文假定FLTD初级源出口半径保持7.5 m,同轴水线长度保持4 m,MRTL长度为3.5 m-
。电路模拟中假定负载为短路,短路电感为1.11 nH
。
Tunel凋亡检测示:两组均可见到凋亡细胞,实验组多于对照组。两组凋亡指数分别为(17.64±6.97)%及(56.48±7.98)%,AI在实验组比对照组增加,且差异有明显的统计学意义(P<0.05)。见图1。
图10给出了不同分层数情况下,装置峰值短路电流随中心汇流区半径的变化规律。可以看出,对于给定的初级脉冲源,存在使短路电流最大的中心汇流区半径优化值。分层数
=2、
=2.3 m时,短路峰值电流最大为14 MA;
=4、
=1.8 m时,短路峰值电流最大为17.5 MA。当
=1.0 m、中心汇流区分层数为2和4层时,峰值电流分别为11.3 MA和15.4 MA。

6 结 论
本文在对Z箍缩装置中心汇流区简化基础上,给出了一种快速计算中心汇流区电感的方法,分析了典型结构参数对中心汇流区电感和装置负载短路电流的影响,获得如下结论。
对表4内数据进行加权平均,求得区域内平均速度V和平均饱和度S,方案1为:V=30.44 km/h,S=0.3187;方案2为:V=32.81 km/h,S=0.2913.
(1)本文电感计算方法获得国际上典型Z箍缩装置的中心汇流区电感与文献最大误差为3.3%。
高分方案数代表来自外部评价指标的设计师产出质量(本实验采用外部专家组评价每一款方案),被引用次数则代表设计师的作品在团队内部的认可度。内外两个指标结合起来可以作为设计师产出质量的一个较全面的表征。
(2)本文获得了中心汇流区电感
随结构参数的变化规律。
随中心汇流区分层数增大而减小;对于给定的分层数,
随中心汇流区半径先减小后增大,存在使中心汇流区电感最小的优化半径。
(3)对于给定的初级脉冲源,存在使装置短路电流最大的中心汇流区半径优化值。对于本文给定装置参数:当分层数
=2、
=2.3 m时,短路峰值电流最大为14 MA;当分层数
=4、
=1.8 m时,短路峰值电流最大为17.5 MA。
:
[1] SPIELMAN R B, STYGAR W A, SEAMEN J F, et al. Pulsed power performance of PBFA Z [C]∥1997 11th IEEE International Pulsed Power Conference. Piscataway, NJ, USA: IEEE, 1997: 709-714.
[2] STYGAR W A, CORCORAN P A, IVES H C, et al. 55-TW magnetically insulated transmission-line system: design, simulations, and performance [J]. Physical Review Special Topics: Accelerators and Beams, 2009, 12(12): 120401.
[3] SAVAGE M E, BENNETT L F, BLISS D E, et al. An overview of pulse compression and power flow in the upgraded Z pulsed power driver [C]∥2007 16th IEEE International Pulsed Power Conference. Piscataway, NJ, USA: IEEE, 2007: 979-984.
[4] SONG S Y, GUAN Y C, ZOU W K, et al. Circuit modeling for PTS’s magnetically insulated transmis-sion lines [C]∥2013 19th IEEE Pulsed Power Conference (PPC). Piscataway, NJ, USA: IEEE, 2013: 1-6.
[5] DENG Jianjun, XIE Weiping, FENG Suping, et al. Initial performance of the primary test stand [J]. IEEE Transactions on Plasma Science, 2013, 41(10): 2580-2583.
[6] DENG Jianjun, XIE Weiping, FENG Shuping, et al. From concept to reality: a review to the primary test stand and its preliminary application in high energy density physics [J]. Matter and Radiation at Extremes, 2016, 1(1): 48-58.
[7] 邹文康. 电流前沿对真空磁绝缘线传输特性的影响研究 [D]. 北京: 中国工程物理研究院, 2015: 39-40.
[8] GRABOVSKY E V, AZIZOV E A, ALIKHANOV S G, et al. Development of X-ray facility “Baikal” based on 900 MJ inductive store and related problems [C]∥28th IEEE International Conference on Plasma Science and 13th IEEE International Pulsed Power Conference. Piscataway, NJ, USA: IEEE, 2001: 773-776.
[9] 蔡红春, 陈林, 蒋吉昊, 等. 热核聚变装置“贝加尔”概念设计 [J]. 强激光与粒子束, 2016, 28(11): 110201-1-110201-7.
CAI Hongchun, CHEN Lin, JIANG Jihao, et al. Conceptual design of thermonuclear facility “Baikal” [J]. High Power Laser and Particle Beams, 2016, 28(11): 110201-1-110201-7.
[10]王勐. 真空轴向绝缘堆闪络概率分析方法研究 [D]. 北京: 中国工程物理研究院, 2006: 103-106.
[11]高巍, 孙广生, 严萍, 等. 纳秒脉冲下真空绝缘沿面闪络特性实验研究 [J]. 高电压技术, 2006, 32(4): 58-61.
GAO Wei, SUN Guangsheng, YAN Ping, et al. Investigation of flashover characteristics under nanosecond pulse in vacuum [J]. High Voltage Engineering, 2006, 32(4): 58-61.
[12]STYGAR W A, LOTT J A, WAGONER T C, et al. Improved design of a high-voltage vacuum-insulator interface [J]. Physical Review Special Topics: Accelerators and Beams, 2005, 8(5): 050401.
[13]HUTSEL B T, CORCORAN P A, CUNEO M E, et al. Transmission-line-circuit model of an 85-TW, 25-MA pulsed-power accelerator [J]. Physical Review: Accelerators and Beams, 2018, 21(3): 030401.
[14]STYGAR W A, CUNEO M E, VESEY R A, et al. Theoretical Z-pinch scaling relations for thermonuclear-fusion experiments [J]. Physical Review: E, 2005, 72(2): 026404.
[15]宋盛义. 圆盘锥磁绝缘传输系统电磁性能及结构力学理论计算 [D]. 北京: 中国工程物理研究院, 2004: 36-39.
[16]STYGAR W A, AWE T J, BAILEY J E, et al. Conceptual designs of two petawatt-class pulsed-power accelerators for high-energy-density-physics experiments [J]. Physical Review Special Topics: Accelerators and Beams, 2015, 18(11): 110401.
[17]倪筹帷, 赵志斌, 崔翔. 考虑位移电流的部分电感计算方法 [J]. 中国电机工程学报, 2017, 37(17): 5181-5187.
NI Chouwei, ZHAO Zhibin, CUI Xiang. Computing method partial inductance for conductor segments by considering displacement current [J]. Proceeding of the CSEE, 2017, 37(17): 5181-5187.
[18]崔翔. 电流连续的细导体段模型的磁场及电感 [J]. 物理学报, 2020, 69(3): 60-71.
CUI Xiang. Magnetic field and inductance of filament conductor segment model with current continuity [J]. Acta Physica Sinica, 2020, 69(3): 60-71.
[19]HE Xu, SUN Fengju, QIU Aici, et al. Four-stage linear transformer driver with sharing shell: EM model, simulation, and performance [J]. IEEE Transactions on Plasma Science, 2021, 49(1): 358-364.
[20]ZHOU Lin, LI Zhenghong, WANG Zhen, et al. Design of a 5-MA 100-ns linear-transformer-driver accelerator for wire array Z-pinch experiments [J]. Physical Review: Accelerators and Beams, 2016, 19(3): 030401.
[21]陈林, 邹文康, 谢卫平, 等. 1 MV/100 kA快脉冲直线型变压器驱动源装置设计 [J]. 高电压技术, 2012, 38(4): 935-940.
CHEN Lin, ZOU Wenkang, XIE Weiping, et al. Design of the 1 MV/100 kA fast linear transformer driver generator [J]. High Voltage Engineering, 2012, 38(4): 935-940.
[22]CONTI F, VALENZUELA J C, FADEEV V, et al. MA-class linear transformer driver for Z-pinch research [J]. Physical Review: Accelerators and Beams, 2020, 23(9): 090401.
[23]CHEN Lin, ZOU Wenkang, ZHOU Liangji, et al. Development of a fusion-oriented pulsed power module [J]. Physical Review: Accelerators and Beams, 2019, 22(3): 030401.
[24]石琦, 邱爱慈, 王志国, 等. 内置触发方式下单级FLTD触发脉冲参数及影响因素 [J]. 西安交通大学学报, 2020, 54(6): 51-57.
SHI Qi, QIU Aici, WANG Zhiguo, et al. Characteristics and influencing factors of one-stage FLTD trigger pulse with internal trigger brick mode [J]. Journal of Xi’an Jiaotong University, 2020, 54(6): 51-57.
[25]STYGAR W A, CUNEO M E, HEADLEY D I, et al. Architecture of petawatt-class Z-pinch accelerators [J]. Physical Review Special Topics: Accelerators and Beams, 2007, 10(3): 030401.
[26]FAN Siyuan, WEI Hao, GONG Zhenzhou, et al. Analytic model and optimization of transmission-line impedance transformers for tens of MA-class pulsed power accelerator [J]. IEEE Transactions on Plasma Science, 2021, 49(10): 3162-3172.
